惯性稳定平台角振动被动减振建模与参数优化
李明,张任强
(北京航空航天大学仪器科学与光电工程学院,北京100191)
高分辨率对地观测系统广泛应用于军事侦察、基础测绘、灾害监测等领域。由于外部环境和自身扰动等因素的影响,摄像载荷难以保持理想的稳定状态,使得视轴失稳,导致成像质量下降,分辨率降低[1-3]。为提高成像质量,可将惯性稳定平台安装于飞行器和遥感载荷之间,利用惯性稳定平台有效隔离载体的扰动及非理想姿态运动,为摄像载荷提供稳定的工作环境,提高对地观测的精度[4-7]。
载体运动以及其他扰动作用于惯性稳定平台形成不同的扰动力矩,在扰动力矩的作用下惯性稳定平台会发生受迫振动,当振动频率接近平台系统固有频率时会引发共振,导致稳定平台无法正常工作[8-11]。因此,为了提高惯性稳定平台的稳定精度,需要进行振动抑制。
振动抑制方法主要包括被动减振和主动减振,由于被动减振方法不需要依靠外部能源,具有结构简单、可靠性好、成本低等特点,已被广泛应用于惯性稳定平台减振[12-20]。
1 振动系统数学模型
1.1 单自由度振动系统
正文部分需给出系统设计的具体应用振动系统分为线振动系统与角振动系统,对于单自由度振动系统,以牛顿第二定律为基础,角振动系统如图1所示。

图1 角振动系统
角振动系统的运动微分方程可表示为:

其中,J为系统转动惯量;Cθ为系统阻尼系数;Kθ为刚体角刚度;分别为系统振动时旋转轴的角加速度、角速度和角位移;Td为引起系统振动的外部干扰力矩。根据式(1)可得角振动系统固有角频率。
1.2 单自由度系统受迫角振动
系统在外界激励作用下产生的角振动称为强迫角振动或受迫角振动,外界激励一般为时间的函数,而一般的周期性激励可以通过傅里叶级数展开成简谐激励的叠加,所以研究简谐激励下的单自由度系统受迫角振动是进行系统角振动减振研究的基础。
由式(1)可得,简谐激励下的单自由度角振动系统的运动微分方程为:
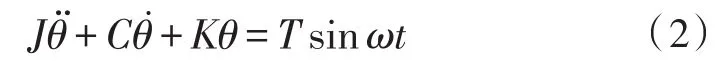
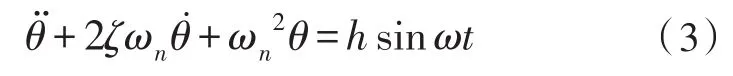
式(3)所示的微分方程的全解等于齐次方程的通解θ1(t)与非齐次方程的特解之和θ2(t),微分方程的全解为:

θ1(t)为单自由度有阻尼自由角振动微分方程的解,得:

设特解θ2(t)=Bsin(ωt-φ),将其代入式(3)并化简,得:
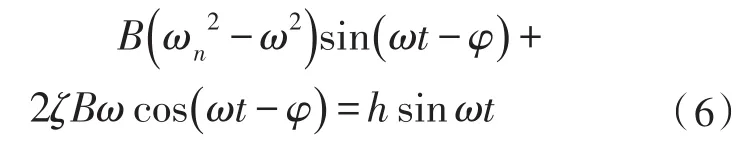
解得:

简谐激励下的单自由度角振动系统的运动微分方程的解由两部分构成:θ1(t)是瞬态响应,包括由初始状态引起的自由振动和干扰力矩引起的自由振动,它们随时间的推移而消失;θ2(t)是稳态响应,代表与激振力矩同频率的强迫角振动,这也是研究系统角振动响应的重点。
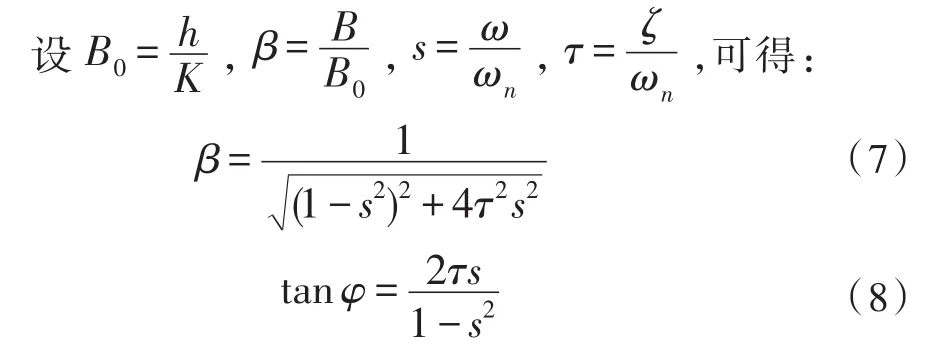
式(7)、(8)分别称为单自由度系统受迫角振动稳态响应的幅频特性和相频特性。可知,稳态响应的振幅和相位只取决于系统本身的物理性质(J、C、k)和激振力矩的频率和幅值,而与系统的初始条件无关。通过改变系统阻尼比可以调节系统稳态输出幅值,进而避免激励频率等于系统固有频率时产生的共振。
2 被动减振系统建模与参数优化
动力吸振是通过将减振装置安装于主系统,通过能量转移实现主系统振动抑制。由其原理可知,该方法可以对扰动力矩作用下惯性稳定平台产生的角振动进行抑制。以单轴稳定平台为例,将安装了减振装置的单轴稳定平台看作两自由度角振动系统,系统等效模型如图2所示。

图2 安装了减振装置的单轴稳定平台系统等效模型
根据单自由度系统受迫角振动数学模型建立两自由度角振动数学模型,建立微分方程组:
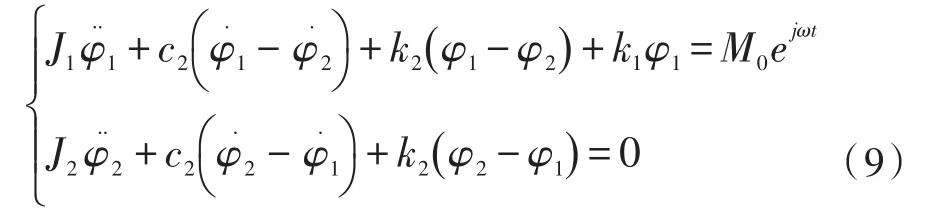
式中:J1稳定平台转动惯量,k1稳定平台转动刚度,J2减振装置转动惯量,c2减振装置阻尼系数,k2减振装置转动刚度,φ1为稳定平台输出角,φ2为减振装置输出角。
对方程组(9)进行拉氏变换,整理得:
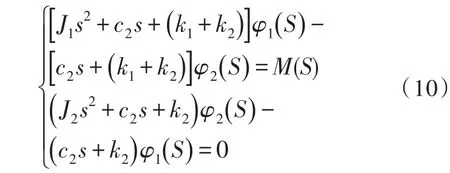
由方程组(10)可得:
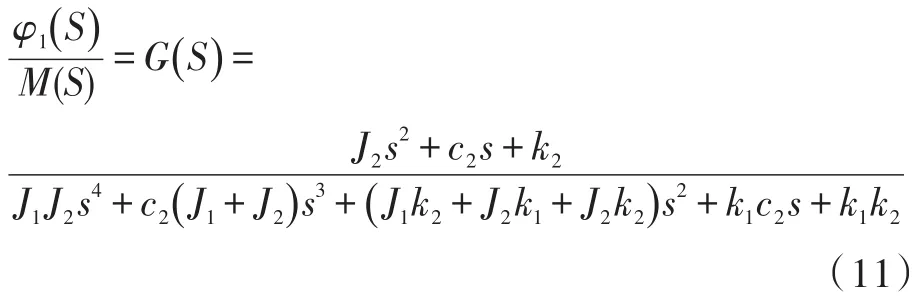
将式(11)由S域转换为频域,可得单轴稳定平台输出角φ1的频率特性:
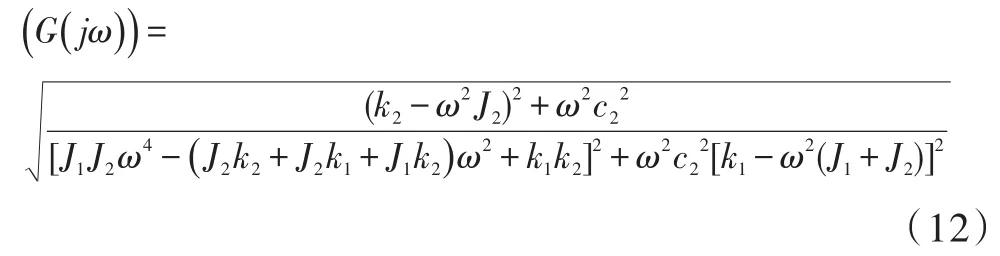
由式(12)可知,平台角振动响应与吸振装置的参数(转动惯量、阻尼系数、转动刚度)相关,需要对吸振装置参数进行计算与优化,使稳定平台系统做受迫角振动时振动幅最小,从而获得最优的减振效果。
首先,对稳定平台受迫角振动进行两种极限条件下的分析,即减振装置阻尼系数c2=∞和c2=0:
1)当c2=∞,即减振装置的阻尼为无穷大时,安装了减振装置的稳定平台系统可等效为无阻尼单自由度振动系统,稳定平台系统的振幅可表示为:
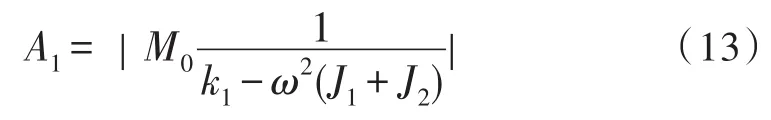
此时,系统有存在一个固有频率。
2)当c2=0,即减振装置的阻尼系数为零时,安装了减振装置的稳定平台系统可等效为两自由度无阻尼角振动系统,稳定平台系统的振幅可表示为:
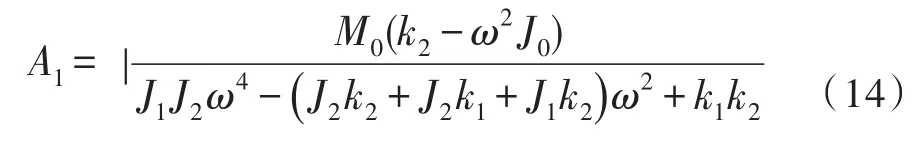
此时,系统存在两个固有频率。
参考单自由度系统受迫角振动稳态响应的幅频特性表达式(8),设,由式(12)得:

式(15)为安装了吸振装置的稳定平台输出角振动幅频特性表达式。
当减振装置阻尼c2=0时,得:

当减振装置c2=∞时,得:

由式(16)、(17)可知,两种极限条件下稳定平台系统的响应曲线相交于两点,且交点位置与惯量比t、固有频率比λ和激振力矩输入频率ω相关。经推导,交点的频率方程为:


综上所述,当惯性稳定平台与减振装置的固有频率比λ和转动惯量比t满足条件,且减振装置阻尼比ζ和转动惯量比t满足条件时,安装了减振装置的惯性稳定平台振动响应幅频特性曲线变化最平缓,系统振幅的峰值最小,减振效果最好。
3 数值仿真
利用上文推导的减振装置参数优化条件,在Matlab中进行数值仿真。设固有频率比λ=,惯量比,绘制减振装置阻尼c2=∞和c2=0时惯性稳定平台系统的幅频响应曲线:
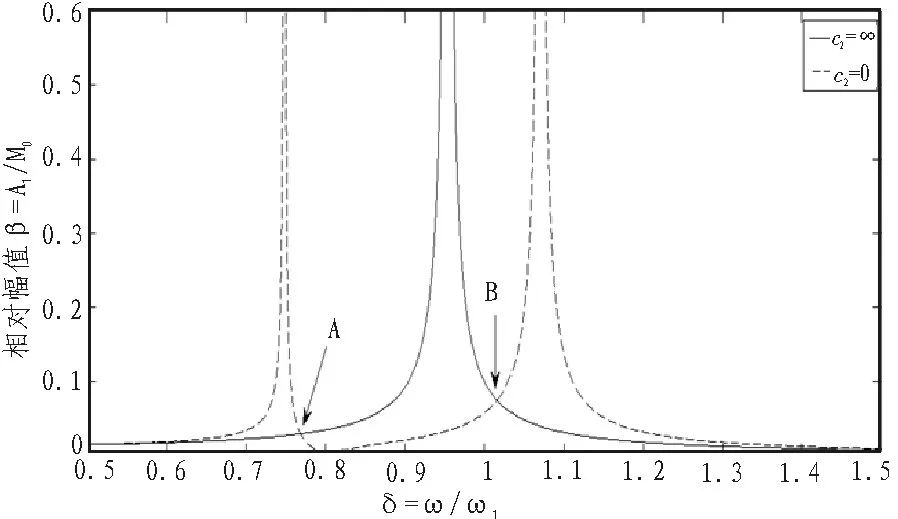
图3 c2=∞和c2=0时惯性稳定平台系统的幅频响应曲线
由图3可知,两条幅频响应曲线相交于A、B两点,一般情况下A、B处幅值不相等。c2=∞时,系统有一个固有频率;c2=0时,系统存在两个固有频率。
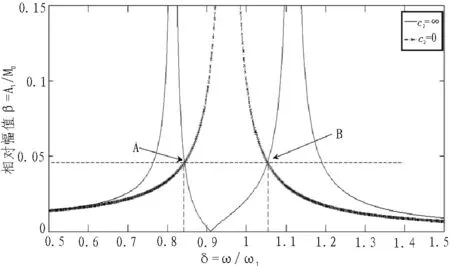
图4 时惯性稳定平台系统的幅频响应曲线
由图4可以看出,当惯性稳定平台与吸振装置的固有频率比和惯量比满足时,c2=∞和c2=0时的惯性稳定平台系统幅频响应曲线的交点A和B幅值相等。
由图5可知:1)不同阻尼比条件下的惯性稳定平台系统幅频响应曲线都通过交点A和B;2)当时,幅频响应曲线的峰值恰好处于交点A、B处,此时系统的振幅最小,幅频特性曲线变化最平缓,减振效果最好。
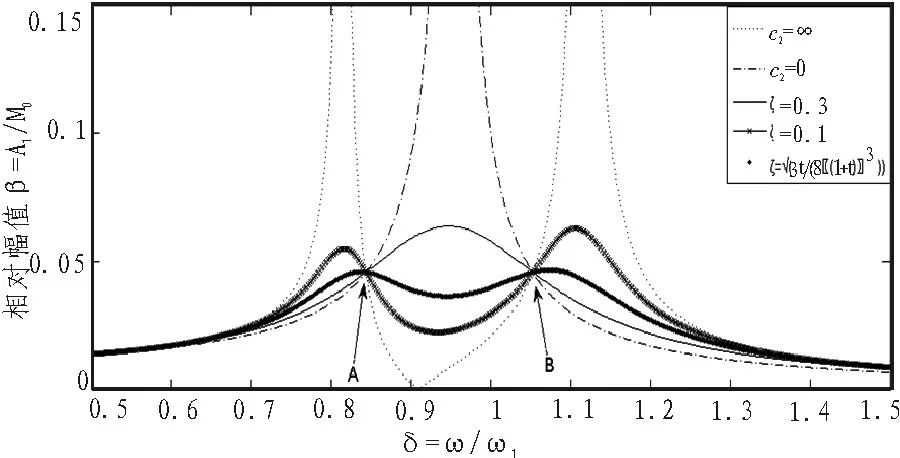
图5 惯性稳定平台系统幅频响应曲线
采用某型航空遥感惯性稳定平台俯仰框参数:J1=0.24 kg∙m2,ω1=69.115 rad/s,采用优化后的参数,即惯量比t=0.1,固有频率比λ=0.909 1,阻尼比ζ=0.169 7时,根据式(9)在Simulink中建模。当输入正弦激励幅值为1 N∙m,频率分别为15 Hz、11 Hz时,未安装减振装置和安装了减振装置的平台响应如图6所示。
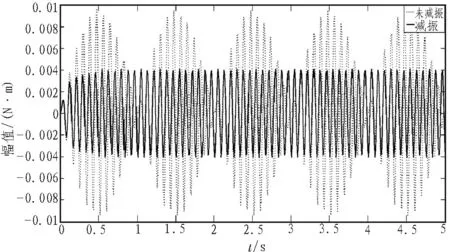
图6 激励幅值为1 N∙m、频率为15 Hz时的平台响应
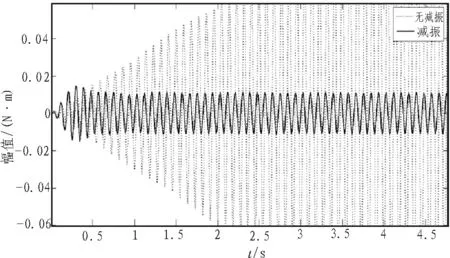
图7 激励幅值为1 N∙m、频率为11 Hz时的平台响应
由图6、图7可知,在稳定平台上安装减振装置,可获得良好的减振效果。如图7所示,当激励频率与原系统固有频率相等时,未安装减振装置的平台系统输出成发散的趋势,产生了共振,安装了减振装置的稳定平台稳态响应平稳且幅值较小,减振效果明显。
4 结束语
为了实现惯性稳定平台受迫角振动抑制,在分析系统受迫角振动幅频特性的基础上,建立了基于动力吸振原理的惯性稳定平台角振动减振系统模型,推导了减振装置参数优化方法,并通过仿真证明了该方法具有良好的角振动减振效果。但实际应用中,由于受到减振装置材料、安装空间等因素的限制,往往无法获得理论推导的减振效果。因此,需要继续深入研究,通过多种减振方式的有机结合和优势互补,进一步提高对惯性稳定平台受迫角振动的抑制能力。
[1]李德仁,李明.无人机遥感系统的研究进展与应用前景[J].武汉大学学报(信息科学),2014,39(5):505-513.
[2]杨秀彬,常琳,金光.单框架控制力矩陀螺转子动不平衡对遥感卫星成像的影响[J].中国光学,2012,5(4):358-365.
[3]ZHOU Xiang-yang,YU Rui-xia,LI Jian-ping,et al.Structure optimal design of roll gimbal for an aerial three-axis ISP based on FEM modal analysis[C]//IEEE ProceedingsofICMTMA.Shanghai China,2011:373-376.
[4]刘仲宇,张涛,刘家燕,等.航空遥感惯性稳定平台内外框架拓扑优化设计[J].中国惯性技术学报,2015,23(4):429-433.
[5]阴蕊,房建成,钟麦英.航空遥感用三轴惯性稳定平台动力学建模与仿真[J].中国惯性技术学报,2011,19(6):676-680
[6]Bao WL,Huang XL,Yin H,et al. Adaptive dynamic friction compensation for an electrooptical platform inertial stabilization system[J].Electronics Optics& Control,2012,19(4):50-54.
[7]Peshekhonov V.Gyroscopic navigation systems:Current status and prospects[J].Gyroscope and Navigation,2011,2(3):111-118.
[8]李贤涛.航空光电稳定平台扰动抑制技术的研究[D].中国科学院长春光学精密机械与物理研究所,2014.
[9]曾德林,肖凯,张力,等.航空遥感惯性稳定平台LuGre摩擦参数的分步辨识[J].光学精密工程,2016,24(5):1148-1158.
[10]李贤涛,张葆,沈宏海.基于自抗扰控制技术提高航空光电稳定平台的扰动隔离度[J].光学精密工程,2014,22(8):2223-2231.
[11]刘思超.陀螺稳定平台振动漂移性能研究[J].战术导弹技术,2014(2):91-94.
[12]张尧,张景瑞.隔振平台对姿态控制系统影响分析及参数选择[J].宇航学报,2013,34(5):657-664.
[13]黄庭轩,张尧,徐世杰.飞轮隔振平台组合系统的动力学建模[J].北京航空航天大学学报,2013,39(1):120-125.
[14]周向阳,刘炜.航空遥感稳定平台振动特性分析与隔振系统设计[J].中国惯性技术学报,2012,20(3):266-272.
[15]梁爽.无角位移减振装置机理研究[D].长春理工大学,2011.
[16]王平,王伟,金伟,等.机载光电侦查平台复合减振设计[J].光学机密工程,2011,19(1):83-89.
[17]周亚东,董萼良,吴邵庆,等.惯性导航平台角振动抑制技术[J].东南大学学报:自然科学版,2013,43(1):60-64.
[18]辛迈,耿健,王洪磊,等.基于振动分析的动力机组无线监测系统设计[J].工业仪表与自动化装置,2016(6):100-101,108.
[19]李凯,许洪华,马宏忠,等.GIS针尖类局部放电引起的振动特性研究[J].陕西电力,2016(9):80-84.
[20]呼志广.500 MW汽轮机低压缸振动分析及处理[J].陕西电力,2014(9):101-104.

