曲率半径对小半径匝道弯桥抗倾覆性能影响

李云州 李绍松 裘是

(厦门大学建筑与土木工程学院土木工程系 福建厦门 361005)

1 匝道弯桥特点

国内弯梁桥结构主要有3大类，包括预应力混凝土结构、普通钢筋混凝土结构以及钢混结构。它们的结构主要截面形式均为箱形截面，原因是箱形截面的抵抗弯矩和抵抗扭矩能力很强，相比于其他类型截面能够最大限度地保证桥梁的稳定，在小半径匝道弯桥中更是如此。

匝道弯桥的特点主要有以下3点：一是桥梁宽度比较窄，正常只有6m～11m，一般是一到两个车道；二是匝道的作用是车辆改变行驶方向，因此匝道的曲率半径不会太大，一般都是小半径桥梁；三是匝道桥往往设置较大的纵坡，并且跨度较大[1]。

2 工程概况

某城市互通立交桥，共拥有7条不同的匝道，均由不等跨的多联所组成，其曲率半径分别为72.5m、285m、400m、450m、560m。桥跨组成形式为最小联为2跨，最大联为4跨，最小跨径为25m，最大跨径为40m。箱梁高度为1.8m，宽度为7.5m，采用的是单箱单室截面，C50等级的混凝土，预应力混凝土桥，预应力筋为Φs15.20，弹模为1.95×105MPa。桥梁设计荷载为公路一级，设计速度为40km/h，采用双曲面球型减隔震支座[2]。

3 有限元计算

(a)72.5m (b)100m

使用有限元软件ANSYS，建立曲率半径分别为72.5m、100m、200m、300m、400m的小半径匝道弯桥有限元模型，其中边墩支座间距为1.9m，中墩为单支座支承且无预偏心，如图1所示。预应力混凝土箱梁采用solid65单元模拟混凝土，采用link180单元来模拟预应力钢筋，同时选择初应变法来模拟预应力的作用。经计算且考虑20%预应力损失后，将腹板位置预应力筋束的初始应变设置成0.00 458，将顶板及底板位置预应力筋束的初始应变设置成0.00 572。加载方式从0开始不断增大荷载，对比处于相同关键状态时的荷载值，以分析不同曲率半径对匝道弯桥抗倾覆性能影响。

4 支座反力分析

对各座弯桥从0开始逐渐增大荷载，研究不同车道荷载倍数下弯桥的支座反力变化情况，计算结果如图2所示。

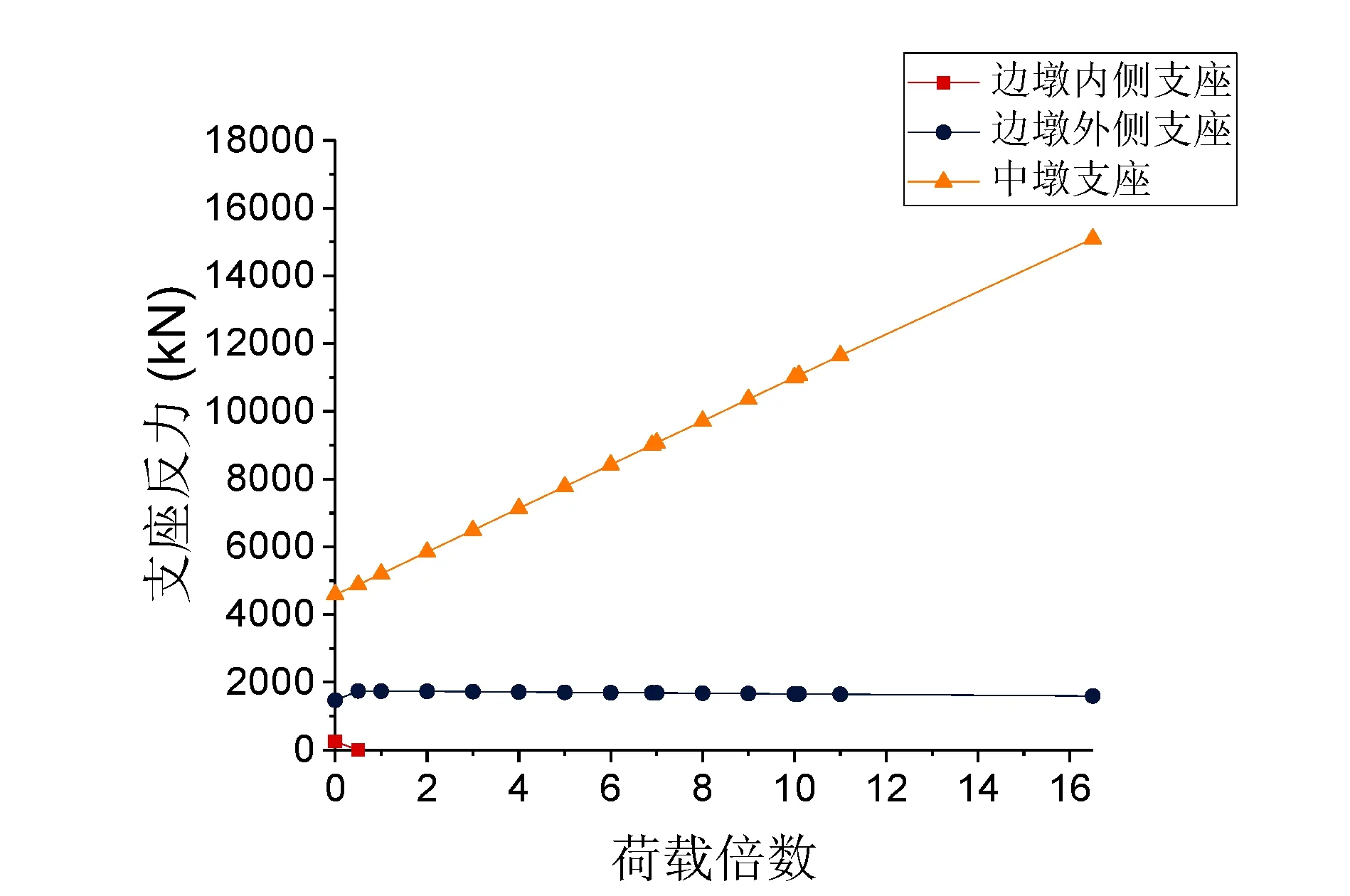
(a)72.5m

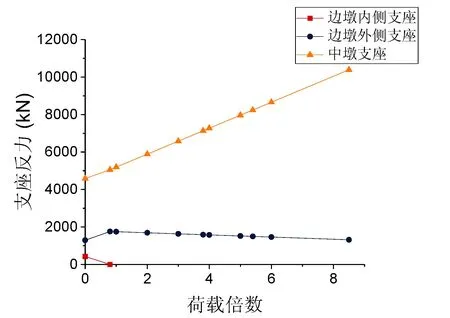
(b)100m

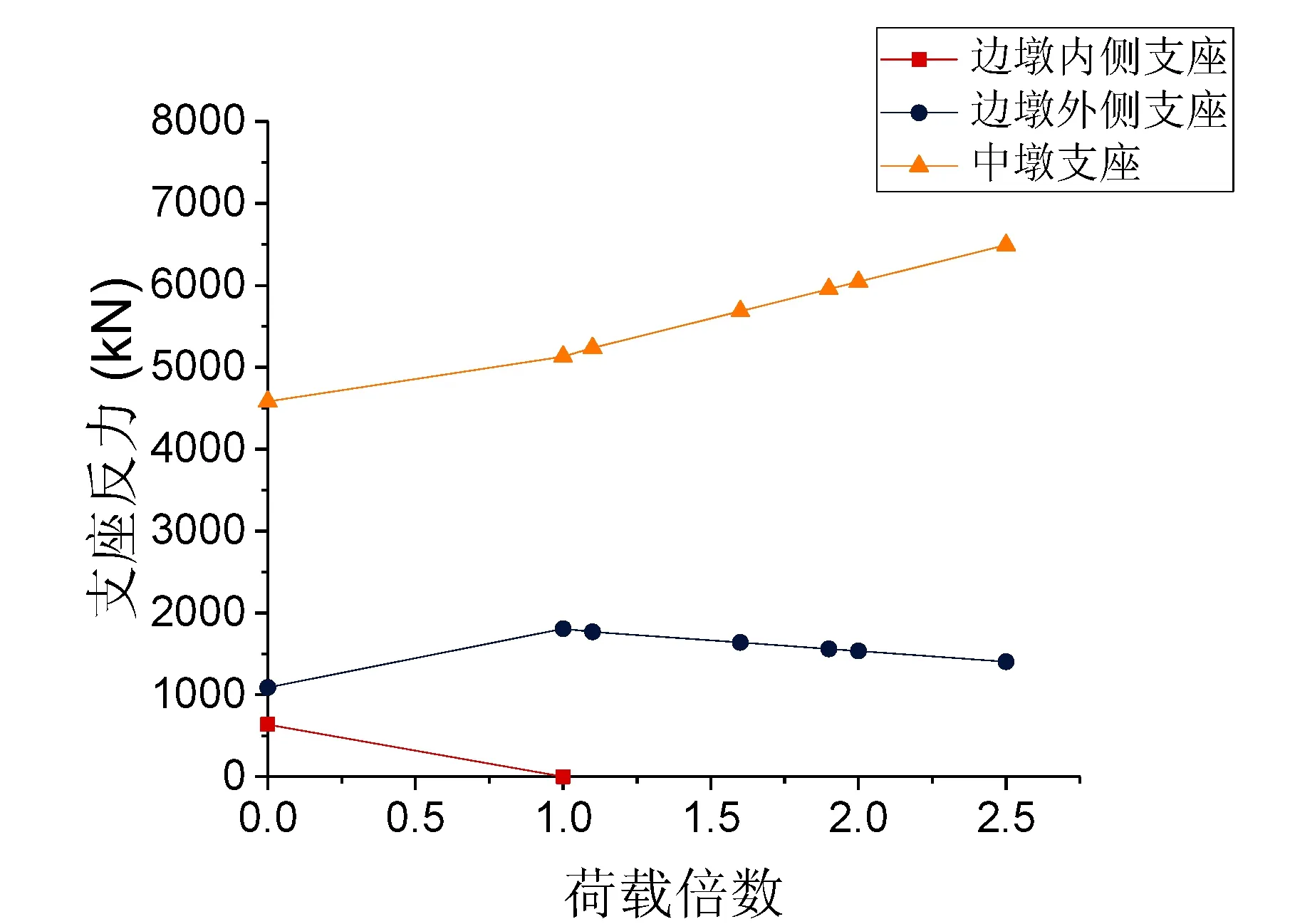
(c)200m

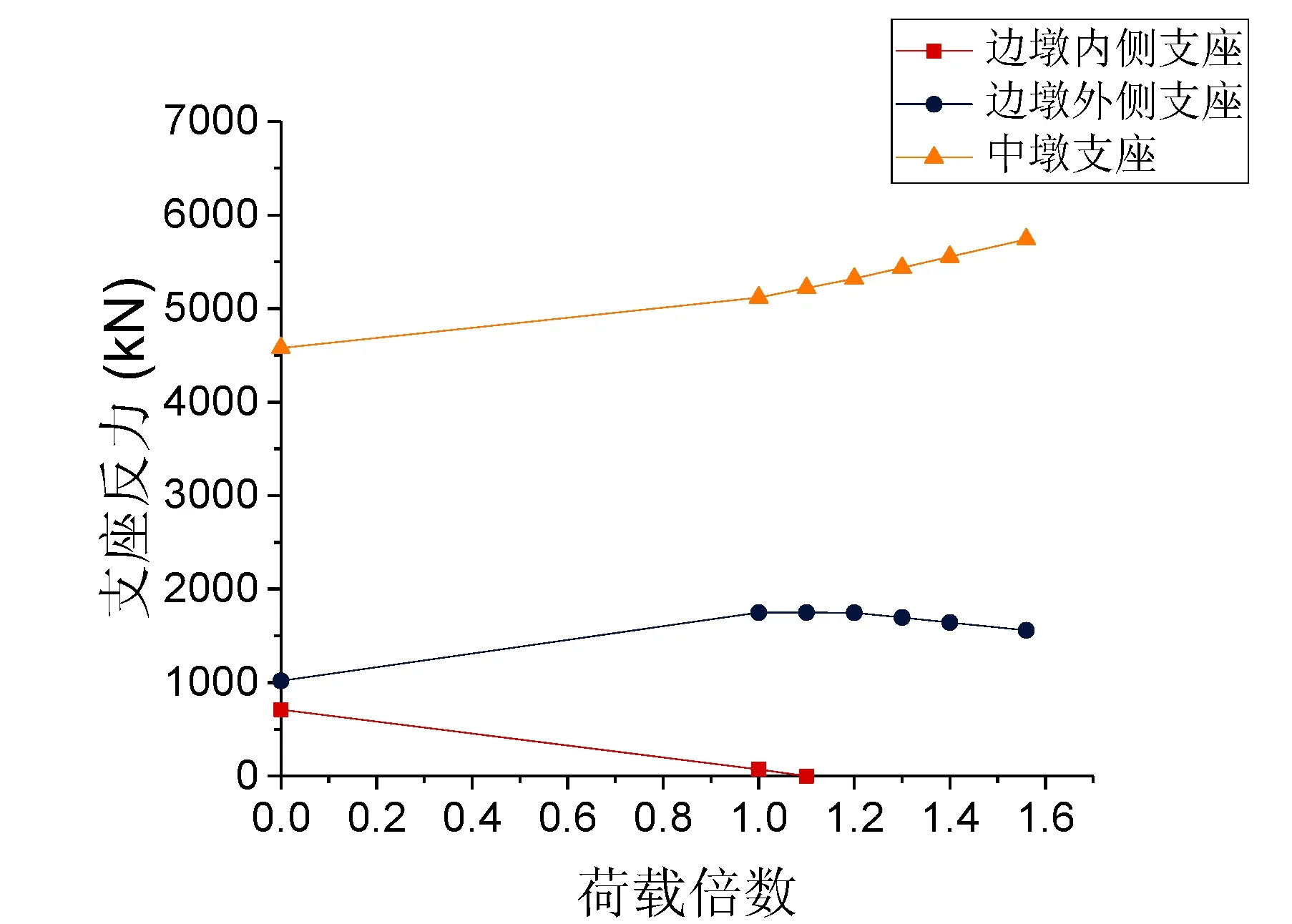
(d)300m

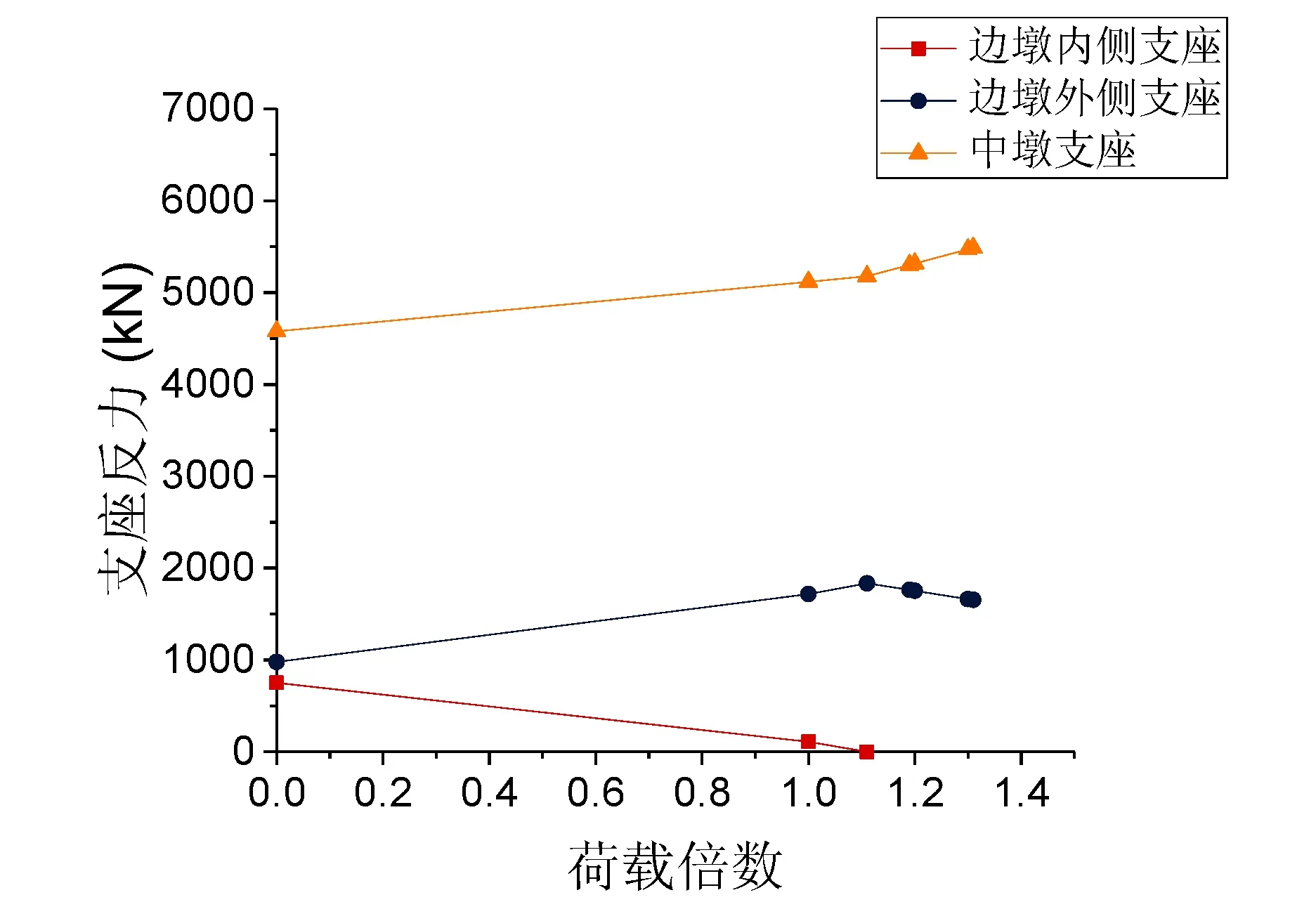
(e)400m图2 不同曲率半径匝道弯桥支座反力变化曲线

由图2分析得出，内侧支座的支座反力随着荷载的增长不断减小，而且较小半径匝道弯桥的内侧支座反力始终小于较大半径匝道弯桥，且比较大半径匝道弯桥更快地发生内侧支座脱空，进入第一关键状态。但相比曲率半径较小的弯桥，曲率半径较大的弯桥会更快地进入倾覆状态。

同时可以得到，匝道弯桥边墩外侧支座的支座反力在边墩内侧支座脱空前，都是随着荷载的增大逐渐变大的，但在边墩内侧支座脱空之后，结构支承体系改变，其支座反力随着荷载的增加逐渐变小。而中墩支座的支座反力则是在不断增大，且在边墩内侧支座脱空之后，增速加快。

5 梁体转角分析

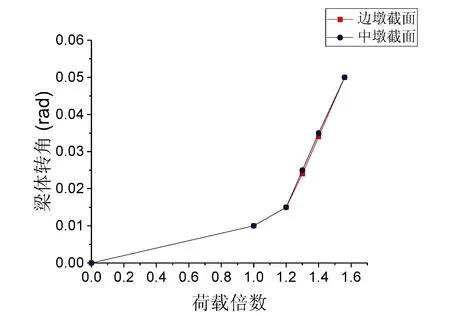
当支座完好，能够对梁体进行有效约束时，梁体的转角接近为0，但当桥梁内侧支座破坏，超过第一关键状态时，梁体转角就会不断增大，引发桥梁倾覆。现在计算不同曲率半径匝道弯桥的梁体转角随荷载增大的变化规律，计算结果如图3所示。

由图3分析得出，所有匝道弯桥在边墩内侧支座脱空前，梁体转角都很小，几乎可以忽略。但在边墩内侧支座脱空之后，随着荷载的增加，梁体转角迅速变大，且曲率半径越大的弯桥转角增速越快，会更快地进入倾覆状态。

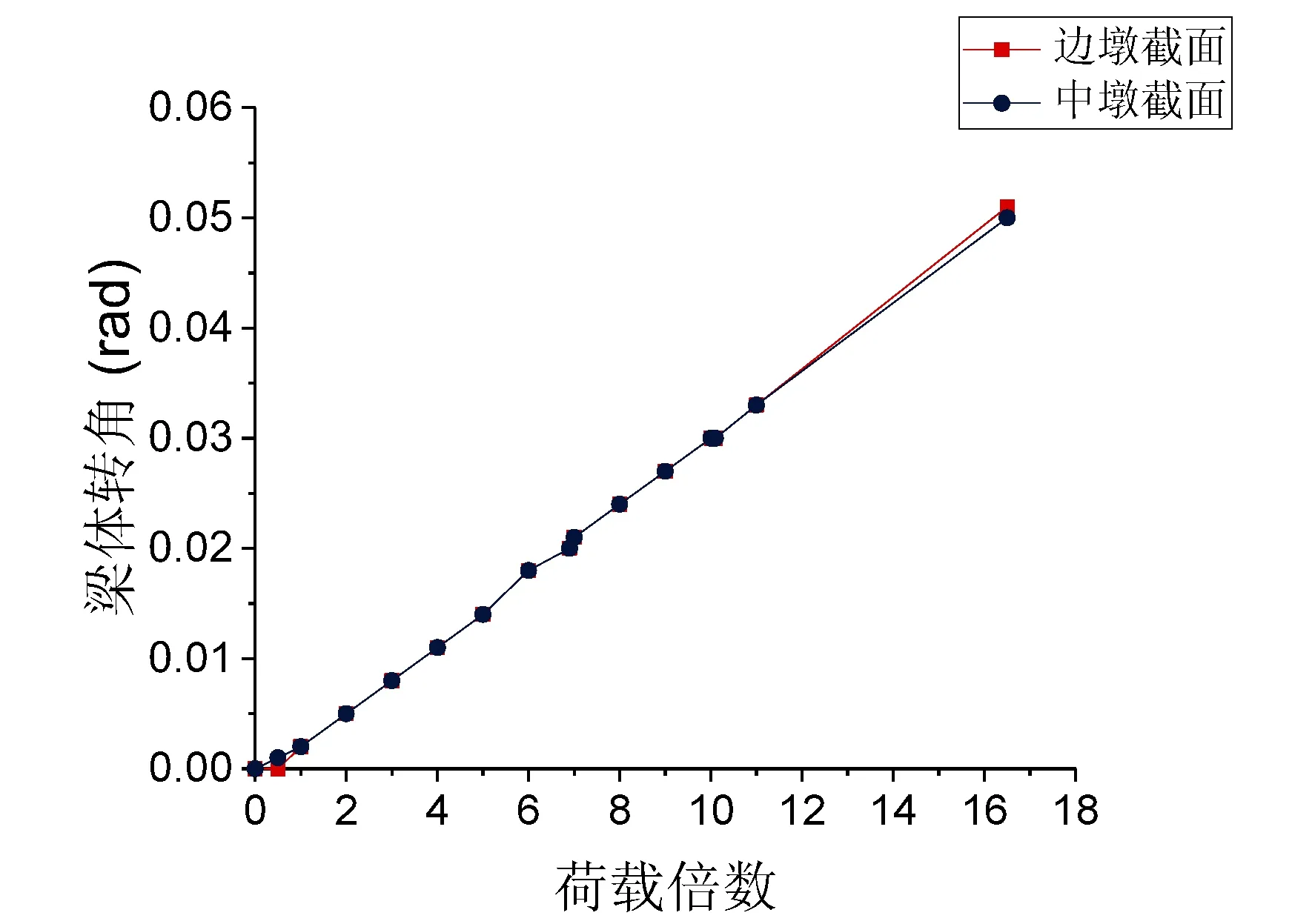
(a)72.5m

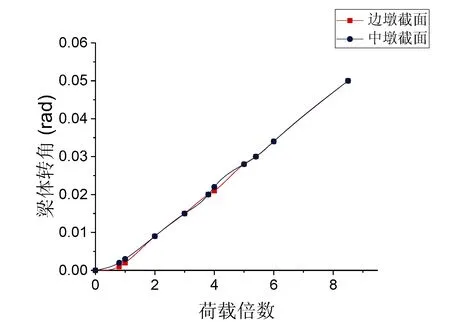
(b)100m

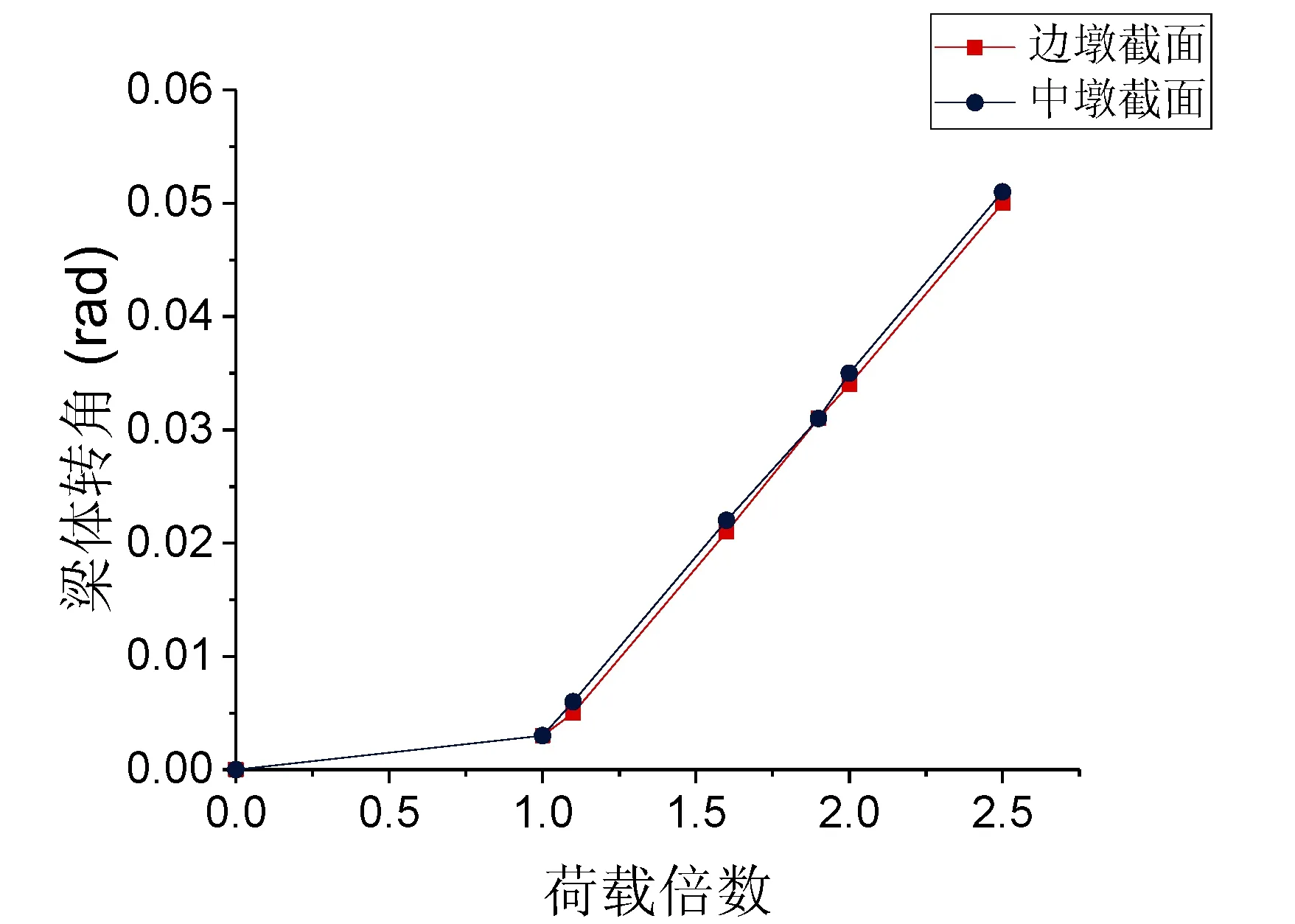
(c)200m

(d)300m

(e)400m图3 不同曲率半径匝道弯桥梁体转角变化曲线

6 抗倾覆稳定系数计算对比

下文对比由桥梁规范[3]方法计算得到的抗倾覆稳定系数与本文有限元方法计算所得的系数。荷载采用规范中的一级车道荷载，并按最不利情况偏载布置，弯桥基频及冲击系数如表1所示。

表1 匝道弯桥基频以及冲击系数

由几何关系计算得到车道荷载集中力到倾覆轴线垂直距离e，车道线与倾覆轴线所围成的面积Ω以及各支座到倾覆轴线的垂直距离Xi，具体数值见如表2～表4所示。

表2 参数取值表

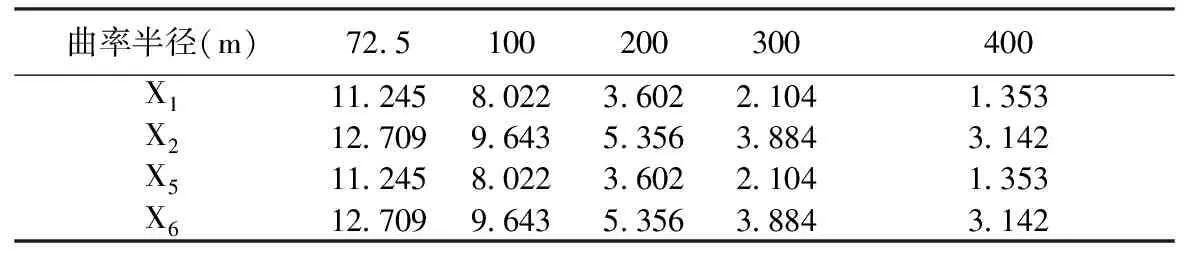
表3 各支座到倾覆轴线距离表

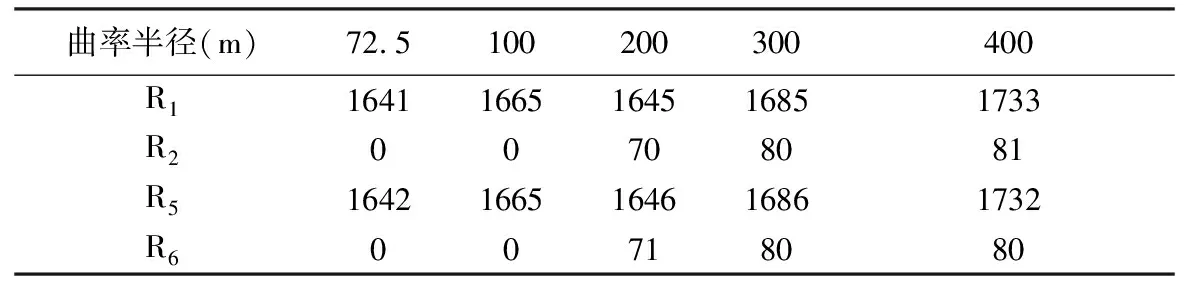
表4 支座反力表

将规范方法计算所得抗倾覆稳定系数与本文有限元方法计算得到的系数对比，结果如表5及图4所示。

表5 不同方法计算得到的匝道弯桥抗倾覆稳定系数

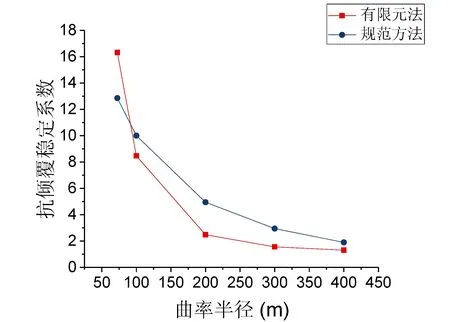
图4 匝道弯桥抗倾覆稳定系数对比图

由表5及图4数据分析得出，随着曲率半径的增长，匝道弯桥的抗倾覆稳定系数不断变小，意味着抗倾覆稳定性能不断减弱。同时，对于曲率半径为72.5m的弯桥，由规范方法计算得到的抗倾覆稳定系数小于有限元方法所得的系数，对于曲率半径为100m、200m、300m、400m的弯桥，由规范方法计算得到的抗倾覆稳定系数大于有限元方法所得的系数。

7 关键状态分析

为了更加直观地表现不同曲率半径中墩单支座匝道弯桥的抗倾覆性能，表6～表7中列出了它们在达到各关键状态时的车道荷载倍数以及安全系数。

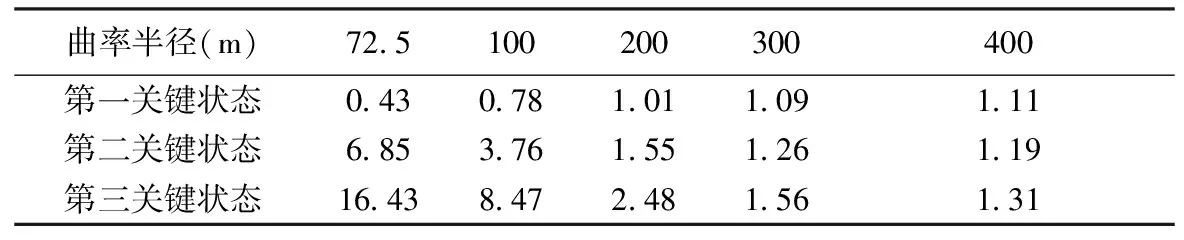
表6 不同曲率半径中墩单支座匝道弯桥达到各关键状态时的车道荷载倍数

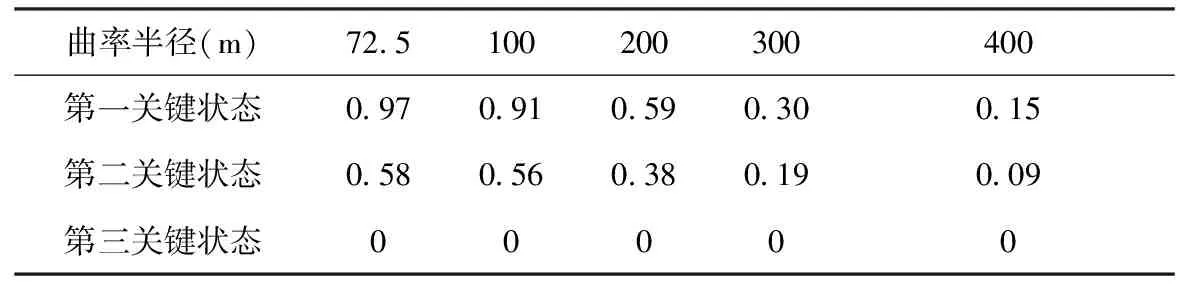
表7 不同曲率半径中墩单支座匝道弯桥达到各关键状态时的安全系数

由表6可知以下规律：

(1)随着曲率半径的增大，达到第一关键状态所需的荷载越来越大，即越来越不容易发生支座脱空。

(2)随着曲率半径的增大，达到第二、第三关键状态所需的荷载越来越小，即越来越容易发生倾覆。

由表7可以总结出，随着曲率半径的增大，匝道弯桥处于第一以及第二关键状态时的安全系数不断减少，也意味着安全储备越来越少，在边墩内侧支座脱空之后，很容易发生桥梁倾覆。

8 结论

综上，在边墩内侧支座脱空之后，随着荷载的增加，梁体转角迅速变大，且曲率半径越大的弯桥转角增速越快，会更快地进入倾覆状态。随着曲率半径的增长，匝道弯桥的抗倾覆稳定系数不断变小，意味着抗倾覆稳定性能不断减弱，所以相比曲率半径较小的弯桥，曲率半径较大的弯桥会更快地进入倾覆状态。

[1] 孙宪魁，杨昀，王磊，等.我国混凝土弯梁桥的现状与发展[J].公路交通科技，2010(5).

[2] 彭天波，李建中，范立础，等.双曲面球型减隔震支座的开发及应用[J].同济大学学报，2007,35(2)：176-180.

[3] JTG D60-2015 公路桥涵设计通用规范[S].北京：人民交通出版社，2015.