双柱型花瓶墩系梁裂缝成因及影响参数分析

翁观旺

(1.长安大学公路学院 陕西西安 710064； 2.深圳市市政设计研究院有限公司 广东深圳 518029)

0 引言

双柱型花瓶墩作为城市高架桥梁常用的墩柱形式之一，具有纤细美观的优点，因而近几年在国内外被广泛应用。但是其受力复杂，设计难度较大，使用一段时间之后在系梁部位经常会出现裂缝。裂缝的出现不仅对桥墩承载能力造成损害，而且对城市景观建设产生不利影响。本文以某城市高架桥的双柱型花瓶墩出现开裂问题为研究对象，通过软件Midas/Civil和Ansys对其开裂原因和影响其系梁裂缝发展的参数进行了分析。

1 工程概况

该项目为国内某快速系统改造工程的高架桥，包括主线桥梁和8道匝道桥，荷载等级为公路-I级。本次选取主线主跨为4m×32m鱼腹式等截面预应力混凝土连续箱梁，桥面宽16m，下部结构采用双柱型花瓶墩，结构形式如图1所示。墩高7.5m，墩柱为侧面带圆弧的矩形墩柱，厚度1.8m，系梁跨中高度1.2m，厚度1.5m。混凝土标号C40，墩顶配置有15根25mm的HRB335钢筋。

图1 双柱型花瓶墩一般构造图

该桥于2013年通车，2015年业主及施工单位对该高架桥例行日常巡检时发现部分花瓶墩系梁出现裂缝，裂缝位于系梁顶部，并在侧面有延伸。实桥双柱型花瓶墩系梁裂缝分布范围及形态如图2所示。

(a)实桥图片

(b)立面图

(c)平面图图2 实桥双柱型花瓶墩系梁裂缝

2 开裂原因分析

从图2裂缝的位置及分布形态可知，中心轴线左侧裂缝宽度约为0.44mm，右侧两条裂缝宽度分别约为1.3mm和0.8mm，且左右侧裂缝与中心轴线的距离基本相等。裂缝沿纵向贯通桥墩系梁顶部并向底部发展，说明桥墩系梁在横桥向承受很大的拉力，而该双柱型花瓶墩系梁上产生的裂缝即为典型的受力裂缝。基于《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)“撑杆-系杆”体系，通过软件Midas/Civil对双柱型花瓶墩系梁裂缝出现的原因进行了分析。

2.1 撑杆-系杆体系

撑杆-系杆体系基于拉压杆模型，其设计思路是以有限元分析法为理论基础，得到结构的传力路径。假定不考虑混凝土的抗拉作用，将同一方向上主要承受拉应力的区域用拉杆模拟，同一方向上主要承受压应力的混凝土区域用压杆模拟，结点为拉压杆交汇区，从而建立一个替代原结构的拉压杆模型[1]。双柱型花瓶墩拉压杆模型可以简化，如图3所示。

图3 双柱型花瓶墩拉压杆模型

2.2 支座反力计算

通过软件Midas/Civil建立主跨为4m×32m等截面预应力混凝土连续箱梁有限元杆系模型。根据模型计算结果可以得到，恒载条件下单个支座反力为3563kN，活载条件下支反力按偏载和中载分别计算。中载条件下单个支反力均为1541kN，偏载条件下支反力分别为2301kN和1188kN。各种工况条件下的支座反力汇总于表1，表2为承载能力极限状态下支点反力的组合设计值。根据表1和表2计算得到各支座反力，分别进行桥墩系梁承载能力极限状态计算和正常使用极限状态计算。

表1 荷载作用的支点反力汇总

表2 承载能力极限状态支点反力组合设计值

2.3 承载能力极限状态计算

由于双柱型花瓶墩系梁处于外力集中作用点附近，并且截面附近有突变区域，即处于“被扰乱区”[2]，其受力分布不满足平截面假定，沿高度方向的剪应力也不是均匀分布，因此，按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)第8.5.3条以及文献[3]研究成果，对双柱型花瓶墩墩顶的受力进行简化，简化模型如图4所示。

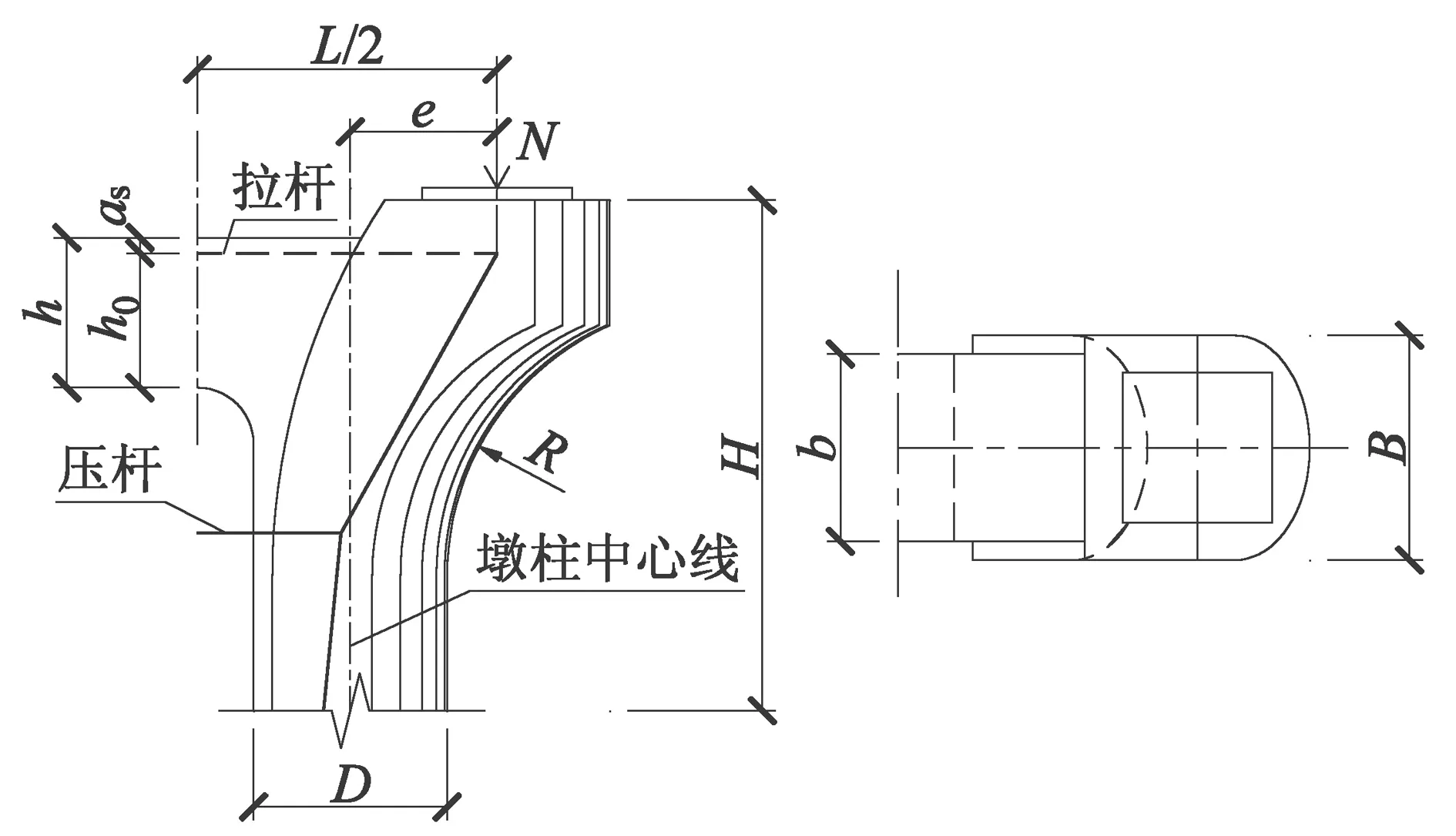
图4 花瓶墩墩顶受力图示

支座偏心e=1.18m，墩柱宽度D=1.55m，墩柱厚度B=1.8m，墩柱高度H=7.5m，系梁长度L=4.8m，墩柱半径R=2.19m，系梁厚度b=1.5m，系梁有效高度h0=1.16m。

支座反力作用下系梁顶部产生的拉力Tz为[3]：

(1)

式中:

△i为系杆力修正系数。

承载能力极限状态下支点反力的组合设计值N=7497kN，则双柱型花瓶墩系梁顶部产生的拉力Tz为：

Tz=0.5334N=0.5334×7497=3999kN

系梁上缘配有15根25mm的HRB335钢筋，其抗拉承载能力Td为：

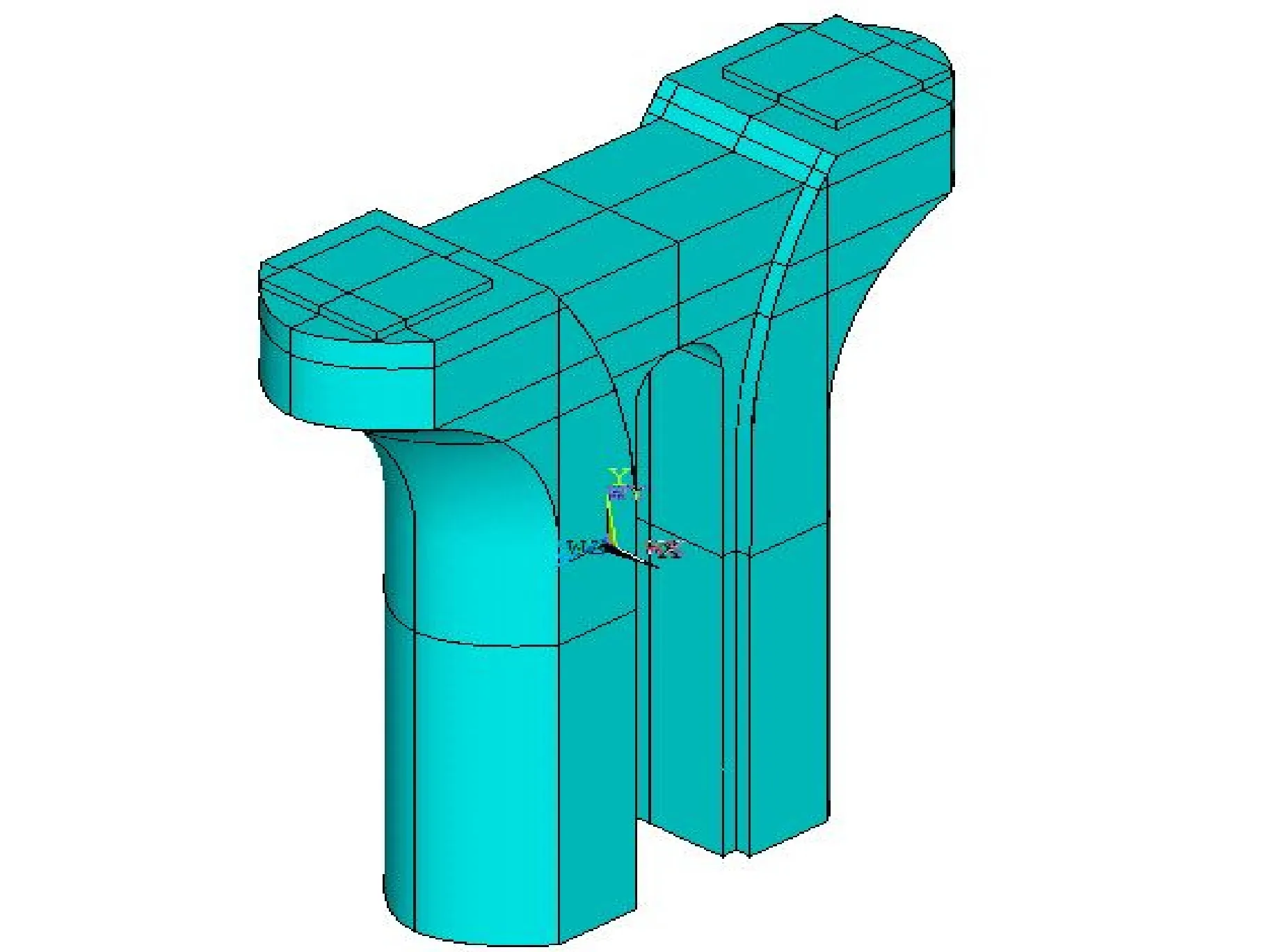
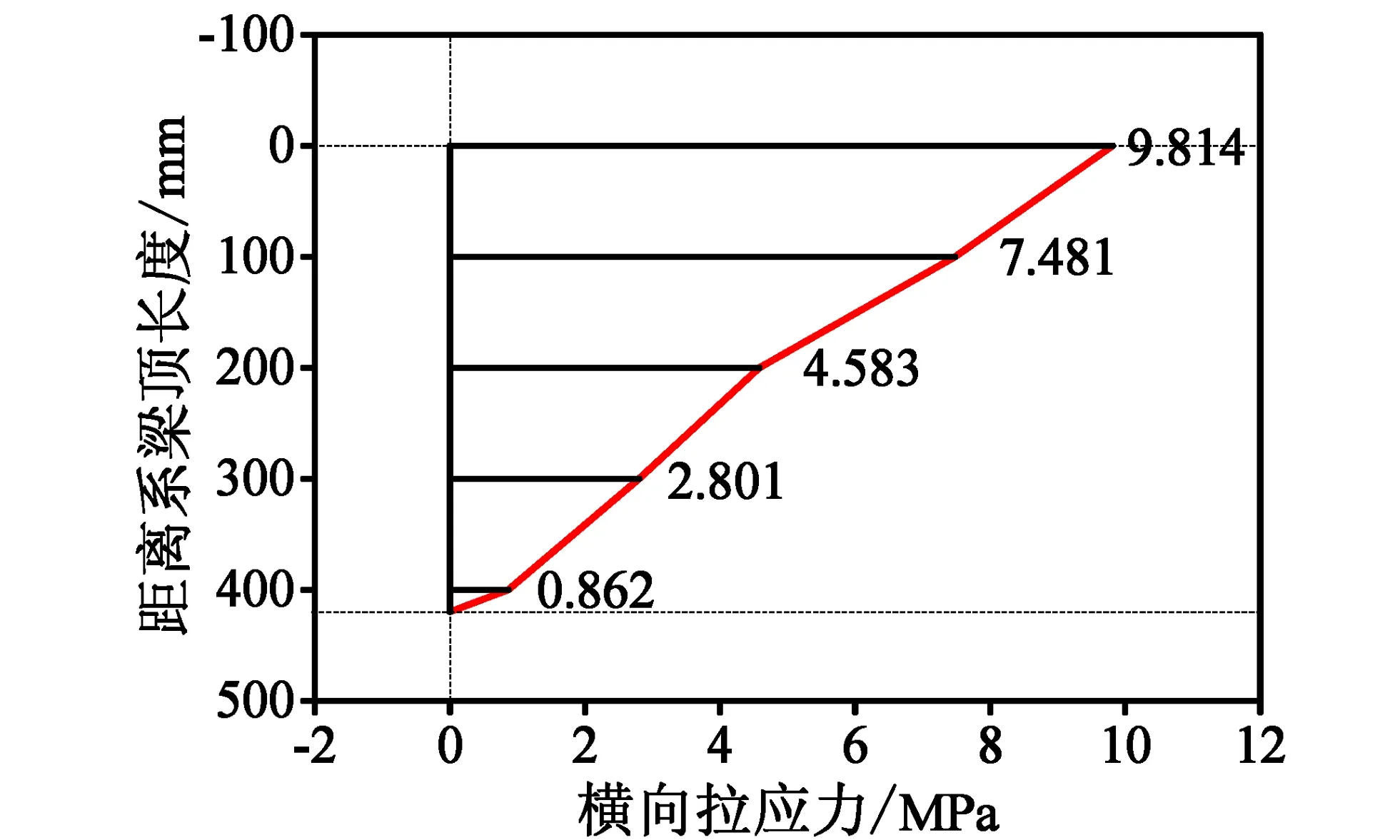
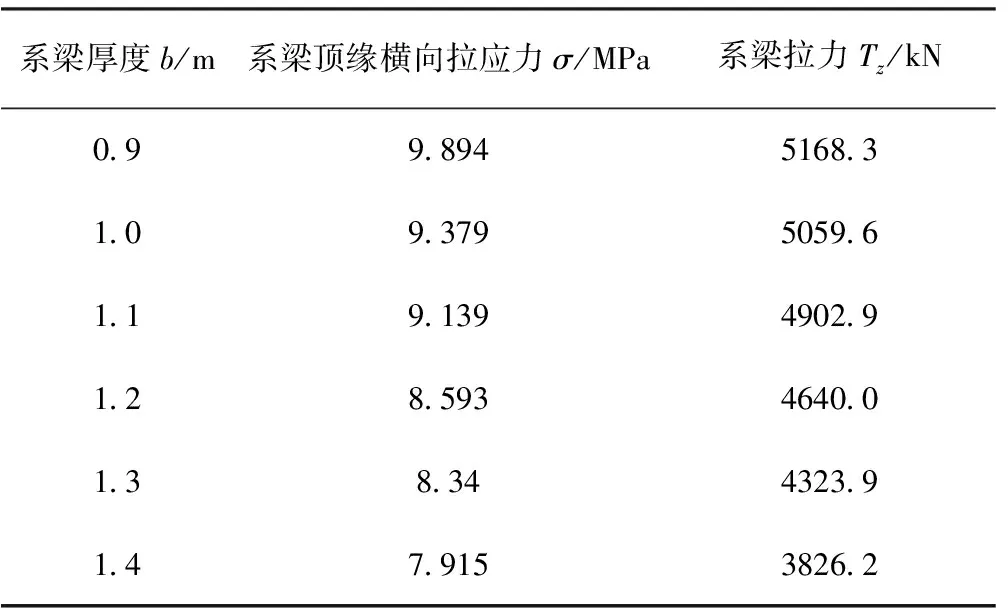
Td=280×7363/1000=2062kN

由此可见，该双柱型花瓶墩系杆的抗拉承载能力远远不能满足要求。

2.4 正常使用极限状态计算

撑杆-系杆体系没有在中国规范正常使用极限状态下的计算方法中使用，现采用美国规范AASH-TO中建议的计算方法[4]。该规范通过钢筋的分布来控制裂缝的发展及其分布范围[5]，计算公式如下：

(2)

式中：

fsa为钢筋的容许拉应力(单位：MPa)；

fy为钢筋的屈服强度(单位：MPa)；

da为受力部位混凝土保护层厚度(单位：mm)，取值不得大于50mm；

A为横截面上与受拉钢筋重心相同的重心位置，并由横截面的轮廓线和平行于中性轴的直线围成的混凝土面积(单位：mm2)；

n为钢筋数目；

Z为裂缝宽度参数(单位：N/mm)，对严重暴露条件下的构件取23 000N/mm，对处于中等暴露条件下的构件不应超过30 000N/mm，对于埋置式结构取17 500N/mm。

根据该双柱型花瓶墩的实际情况及所处的环境条件，取da=35mm，A=105 000mm2，n=15，Z=23 000N/mm，计算可得fsa=168MPa。

根据我国公路桥梁规范对混凝土结构在正常使用极限状态下，进行长期和短期两种荷载效应组合计算，计算结果如表3所示。

表3 正常使用极限状态下系杆钢筋拉应力计算表

由表3中的计算结果可知，短期和长期两种荷载效应下钢筋拉应力值均大于根据美国AASH-TO规范得到的计算值，即正常使用阶段双柱型花瓶墩系梁顶部两个支座间的受拉钢筋数量不足而混凝土拉应力过大，导致系梁顶部出现受力裂缝。

3 参数分析

采用大型有限元软件ANSYS建立实际桥墩的有限元模型，如图5所示。

图5 双柱型花瓶墩有限元模型

模型采用实体单元Solid65，该单元具有8个节点，每个节点有3个自由度，即x，y，z 3个方向的线位移，可对3个方向的含筋情况进行定义。同时，该单元可模拟混凝土的开裂、压碎、塑性变形和徐变，还可模拟钢筋的拉伸、压缩、塑性变形以及蠕变。其中，混凝土弹性模量为3.5×1010N/m2，密度为26 000N/m3，柏松比为0.167，支座反力取恒载和最不利活载产生的支座反力5864kN。

3.1 系梁高度

系梁高度分别取0.6m、0.7m、0.8m、0.9m、1.0m、1.1m、1.2m、1.3m，其他参数保持不变。根据模型计算结果可知，系梁顶缘处于受拉状态。图6展示了系梁高度为0.6m时，系梁沿对称轴竖直方向的横向拉应力，可以看出，横向拉应力沿高度方向并非均匀分布，变化趋势不满足线性关系。表4列出了不同高度系梁的顶缘横向拉应力，可以得出，随着系梁高度的增加，系梁中心顶缘的最大拉应力呈现逐渐下降的趋势。当系梁高度为0.6m时，系梁顶缘跨中的最大拉应力达到9.814MPa，而当系梁高度增加到1.3m时，系梁顶缘跨中的最大拉应力降到6.532MPa，降低了33.4%。对不同高度的系梁拉应力进行积分，求得系梁横桥向拉力Tz如表4所示，其中Tz=应力图面积×系梁厚度。由表4可知，随着系梁高度的增加，由于结构自重的增大以及内力重分布，横向系杆受到的拉力增加，但增速逐渐放缓。

图6 系梁高度0.6m沿对称轴竖直方向的横向拉应力

系梁高度h/m系梁顶缘横向拉应力σ/MPa系梁拉力Tz/kN0 69 8143042 90 78 6453375 60 88 6883911 70 98 4073970 11 07 6423974 41 17 7324123 81 27 0844208 81 36 5324201 1

3.2 系梁厚度

系梁厚度分别取0.9m、1.0m、1.1m、1.2m、1.3m、1.4m，其他参数保持不变。表5列出了不同厚度系梁的顶缘横向拉应力，随着系梁厚度的增加，系梁中心顶缘的最大拉应力呈现逐渐下降的趋势。当系梁厚度为0.9m时，系梁顶缘跨中的最大拉应力达到9.894MPa，而当系梁厚度增加到1.4m时，系梁顶缘跨中的最大拉应力降到7.915MPa，降低了20%。与不同高度的系梁相同，不同厚度系梁的拉应力沿高度方向并非均匀分布，变化趋势不满足线性关系。对不同厚度的系梁拉应力进行积分，求得系梁横桥向拉力Tz如表5所示。由表5可知，随着系梁厚度的增加，横向系杆受到的拉力逐渐减少，且减少速度逐渐变大。

表5 不同高度系梁的横向拉应力及拉力

3.3 系梁长度

系梁长度分别取2.6m、3.0m、3.4m、3.8m、4.2m、4.6m，其他参数保持不变。表6列出了不同长度系梁的顶缘横向拉应力，可以看出，随着系梁长度的增加，系梁中心顶缘的最大拉应力呈现逐渐下降的趋势。当系梁长度为2.6m时，系梁顶缘跨中的最大拉应力达到7.732MPa；而当系梁长度增加到4.6m时，系梁顶缘跨中的最大拉应力降到5.187MPa，降低了32.9%。与不同高度的系梁相同，不同长度系梁的拉应力沿高度方向正应力并非均匀分布，变化趋势不满足线性关系。对不同长度的系梁拉应力进行积分，求得系梁横桥向拉力Tz如表6所示。由表6可知，随着系梁长度的增加，横向系杆受到的拉力逐渐减少，最后趋于稳定。

表6 不同长度系梁的横向拉应力及拉力

4 结论

(1)通过对双柱型花瓶墩承载能力极限状态和正常使用极限状态下结构内力验算可知，双柱型花瓶墩系梁出现裂缝的原因，是系梁顶部普通钢筋配置不足而导致混凝土拉应力过大，使得其抗拉承载能力达不到设计要求。

(2)双柱型花瓶墩系梁处于外力集中作用点附近，且截面构造复杂，突变明显，处于所谓的“被扰乱区”，系梁沿对称轴竖向高度方向的横向拉应力非均匀分布，受力特征不满足平截面假定。

(3)随着系梁高度的增加，系梁中心顶缘的最大拉应力逐渐减少，但系梁受到的拉力逐渐增大，最后趋于稳定；随着系梁厚度增加，系梁中心顶缘的最大拉应力逐渐减少，且系梁受到的拉力逐渐减少，减少速度逐渐变大；随着系梁长度增加，系梁中心顶缘的最大拉应力逐渐减少，且系梁受到的拉力逐渐减少，最后趋于稳定。

[1] 张勇.拉压杆理论在薄壁花瓶墩中的应用研究[D].广州: 华南理工大学, 2010.

[2] 陈志文.混凝土箱梁桥横隔梁的拉压杆模型及配筋设计研究[D].南京: 东南大学, 2012.

[3] 周浩.双柱花瓶墩横向系杆力分析[J].城市道桥与防洪, 2012(6):117-121.

[4] 王曦婧, 叶见曙, 王毅.实体式混凝土桥墩裂缝成因分析及加固方法研究[J].现代交通技术, 2005, 2(5):35-38.

[5] 郑春梅.花瓶墩钢筋应力分析[J].建筑工程技术与设计, 2016(14).