基于差值矩阵分解的推荐算法

成 鹏,刘文斌

(温州大学数理与电子信息工程学院,浙江 温州 325035)

0 引 言

推荐算法主要分为2大类：1)基于内容的推荐算法[1]；2)基于协同过滤的推荐算法。基于协同过滤的推荐算法又可以分为基于邻域的推荐算法(基于用户的协同过滤算法[2]和基于物品的协同过滤算法[3])和基于矩阵分解的推荐算法[4]。基于内容的推荐算法的优点是专业人员根据商品的属性进行分类，方便用户按类查找。基于邻域算法的优点是推荐结果具有很好的解释性且可以实现实时推荐。基于矩阵分解算法的优点是有较好的数学理论基础并且预测结果精度比较高[5]。

2006年Simon[4]首先将改进的SVD模型用于推荐系统的评分预测。2007年多伦多大学的Salakhutdinov等人[6]提出了使用概率矩阵分解来进行评分预测。因为参数的选择对贝叶斯概率矩阵的性能有着重要的影响，但是寻找合适的参数非常耗时。为了解决概率矩阵分解在上述方面的不足，2008年Salakhutdinov等人[7]提出了贝叶斯概率矩阵分解，把参数整合到模型内部，省去了寻找最优参数的过程。同年雅虎研究院的Koren[8]提出了将基于邻域的方法整合进矩阵分解模型。2009年Koren等人[9]发现物品的属性、人的兴趣会随着时间变化而发生改变，将时间模型引入矩阵分解取得了不错的效果。2011香港中文大学的Ma等人[10]率先尝试将社交关系(信任关系)引入矩阵分解，他认为如果2个用户之间存在着社交关系(信任关系)，那么这2个用户品味会比较接近，反映到用户特征向量上也是很相似的。Ma等人在Douban[11]和Epinions[12]这2个提供社交关系(信任关系)的数据集上进行了实验。2013年Yang等人[13]对Ma等人的社交关系(信任关系)进行了细化，提出了Circle-based Recommendation，主要思想是:物品有很多的类别，每一个类别构成了一个Circle，在同一个Circle中用户对其他用户都有信任值，这些信任值构成了信任网络，在每个Circle分别用该Circle的信任网络来约束用户特征向量。2016年梅忠等人[14]考虑到传统矩阵分解技术没有考虑不同评分系统的整体差异以及数据集内部用户与物品存在的固有属性，提出了受约束偏置的概率矩阵分解。同年巫可等人[15]将用户属性二值化，利用分类模型衡量用户属性的重要程度，从而构建了用户相似矩阵，用邻居节点的评分修正预测评分。

在现实生活中，用户评分是存在偏差的。首先即使2个用户对同一部电影的评分相同，他们对该电影的喜好程度也可能是不一样的；其次同一部电影不同年龄、性别、职业的人对其评分具有明显的区别。本文在矩阵分解的基础上提出了差值矩阵分解。将用户对电影的评分减去与其社会属性相似的用户对该电影评分的平均分，得到差值矩阵，进而对差值矩阵进行分解。结果表明在基于年龄和职业的差值矩阵分解较矩阵分解，在80%和60%的训练数据上MAE分别降低了7.8%和3.4%。

1 算 法

1.1 矩阵分解模型(MF)

设所有用户组成的集合为U={u1，u2，…,um}，所有电影组成的集合为V={v1,v2,…,vn},m表示用户的数量，n表示电影的数量。设置rui为用户uu对电影vi的评分，则所有用户对电影的评分组成了评分矩阵R。

表1 评分矩阵R

用户电影v1v2…vnu1r11r12…r1nu2r21r22…r2n︙︙︙⋱︙umrm1rm2…rmn

矩阵分解的主要思想是：将评分矩阵R(如表1所示)近似表示成用户特征矩阵P和电影特征矩阵Q的内积,即R≈P×QT。其中R∈m×n，P∈m×d，Q∈n×d,d为隐特征的个数。矩阵分解的目标是最小化用户对电影实际评分rui与预测的评分之间的误差。最后给模型加入正则项λ(‖pu‖2+‖qi‖2)来防止过拟合。损失函数定义如下:

其中，K为训练集，pu为用户特征向量，qi为电影特征向量,λ为惩罚系数。使用随机梯度下降(Stochastic Gradient Descent,SGD)来更新用户特征向量pu和电影特征向量qi。更新规则如下:

1.2 差值矩阵分解模型(DMF)

将年龄、性别相同的用户(年龄段划分由数据集给出)对同一部电影的评分求平均分后发现，不同年龄、性别对电影的评分相差还是比较大的。如表2表示的不同性别、年龄段的用户对电影Toy Story评分的平均分。

表2 不同年龄、性别段用户对电影Toy Story评分的平均分

年龄性别FM14.07693.8356184.08663.9907254.32514.1584354.23264.3333453.91674.2000504.03334.1154564.266673.7368

受到上面的启发，本文将社会属性相同的用户组成一个group简写为g，不同社会属性的用户共同组成了G={g1,g2,…,gn}。本文分别以年龄、性别、职业、年龄+性别、年龄+职业、职业+性别社会属性建立G{…}。

2 实验结果及分析

2.1 数据集与评价标准

本文实验的数据来自于GroupLens[16]收集并整理的MovieLens 1M数据集。数据包含6040名用户的信息(包括用户ID、性别、年龄、职业、邮编)，3952部电影的信息(电影ID、电影名、电影类别)以及1000209条评分信息(用户ID、电影ID、评分、时间戳)。

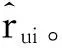
平均绝对值误差MAE定义如下:

2.2 实验设计

为了验证算法的性能,选择3个目前比较流行的评分算法进行对比试验。

1)BPMF[17](Bayesian Probabilistic Matrix Factorization)。设用户的特征矩阵P和电影的特征矩阵Q,服从均值为0方差分别为δP，δQ的高斯分布，建立R，P，Q的联合密度函数,通过最大化后验概率求解用户特征矩阵P和电影特征矩阵Q。

2)MF(Matrix Factorization Techniques For Recommender Systems)。因为传统的SVD矩阵分解技术不适用数据稀疏的情景，MF是SVD矩阵分解的一种变形，MF使用随机梯度下降很好地解决了数据稀疏的问题。

3)融合用户属性隐语义模型。将矩阵分解后的隐特征作为输入，二值化后的用户属性作为标签值,利用logistic为每个属性建立一个分类模型。根据在测试集上的准确率cs确定该属性的重要性,进而根据用户二值化后的属性和属性的重要性建立用户之间的相似度网络。最后用用户u相似用户的评分修正u的预测评分。

此外，本文给出的预测结果都是在各类算法参数最优的情况下取得的。首先分别计算各个方法在参数取(0.00001,0.0001,0.001,0.01,0.1,1)时的MAE，发现参数取0.01和0.1时MAE相对较小。接下来将区间[0.01,0.1]分成10等份去寻找最优参数。

2.3 实验结果分析

为了发现不同社会属性用户的评分模式，本文分别研究年龄、性别、职业以及它们的两两组合对用户评分的影响。隐特征的维度对预测精度有着重要的影响。经过大量的试验，可以发现当隐特征个数超过20后，各类算法预测精度提高非常有限，故本文各个矩阵分解算法隐特征的维度均设定为20。

实验过程中，分别选择80%和60%的训练数据做训练，在剩余数据上进行测试。实验采用交叉验证的方式进行，实验结果如表3所示。

表3 不同方法的平均误差

训练样本数/%方法贝叶斯概率矩阵分解矩阵分解融合用户属性隐语义模型差值矩阵分解-年龄差值矩阵分解-性别差值矩阵分解-职业差值矩阵分解-年龄+性别差值矩阵分解-职业+性别差值矩阵分解-年龄+职业800.69920.67410.67770.66470.66910.65870.65830.64920.6221600.71290.68710.69050.67970.68110.68250.67960.67880.6625

表4 不同方法取最优值时λ的取值

训练样本数/%方法矩阵分解融合用户属性隐语义模型差值矩阵分解-年龄差值矩阵分解-性别差值矩阵分解-职业差值矩阵分解-年龄+性别差值矩阵分解-职业+性别差值矩阵分解-年龄+职业800.030.030.040.050.070.050.060.07600.060.060.070.070.060.070.070.08

从表3中可以看出，在80%和60%的训练数据上，差值矩阵分解预测的精度要高于其他的算法。其中使用年龄和职业信息Group的差值矩阵分解取得的精度最好。表4是不同方法取最优值时λ的取值。

下面分析每个用户对电影评分减去与其社会属性相似用户评分平均值后的绝对值即|zui|，分别从1/4中位数、中位数、3/4中位数、均值、标准差这5个方面进行分析。其中差值矩阵分解-整体表示的是将每一个用户的评分减去所有评分的平均分，统计量信息如表5所示。

中位数、均值和方差越小，从一定程度上可以说明通过该种社会属性进行分组，组内成员的相似度越高。从中位数的角度去观察，可以发现|zui|的中位数越小，MAE也就越小。从均值的角度去观察，可以发现|zui|的均值越小，MAE也就越小。从标准差的角度去观察，可以发现|zui|的方差越小，MAE也就越小。总体而言均值、方差和MAE呈现正相关性。

表5 |zui|的统计量信息

统计量信息方法差值矩阵分解-整体差值矩阵分解-年龄差值矩阵分解-性别差值矩阵分解-职业差值矩阵分解-年龄+性别差值矩阵分解-职业+性别差值矩阵分解-年龄+职业1/4中位数0.41840.30470.30860.29330.29960.27780.2162中位数0.58160.66670.67860.64710.650.62070.53333/4中位数1.41841.08161.10441.06251.0681.01481.0均值0.93370.76340.77520.74580.75140.72120.6565标准差0.6130.57860.58270.5720.57270.56570.5596

从表5可以看出在年龄、性别、职业、年龄+性别、职业+性别、年龄+职业这6个分组中，年龄+职业分组|zui|的中位数在0.53左右而其他分组的中位数都大于0.62，年龄+职业分组|zui|的均值在0.65左右而其他分组的均值都大于0.72。说明以年龄+职业来对用户进行分组，组内用户的评分差异是最小的。所以针对MovieLens 1M数据集来说按年龄+职业进行分组是最佳的选择。

2.4 不同社会属性下参数λ的影响

社会属性不同，差值矩阵分解取得最优解的λ也是一样的，接下来讨论不同的社会属性下，MAE随着λ的变化趋势。如图1，图2所示。

图1 80%训练数据MAE在不同学习速率下的变化情况

图2 60%训练数据MAE在不同学习速率下的变化情况

观察图1和图2可以发现λ从0.00001逐渐增加到1的时候，MAE变化趋势是一致的。先下降然后再上升再下降最后一直上升。λ在两端时，MAE比较大。任何情况下，MAE取得最优解λ取值范围都为0.05～0.09。在λ比较小的时候，误差比较大是由于正则项的权重太小没有能够很好地防止模型的过拟合。而当λ取值较大的时候，模型的误差也比较大，原因是正则项权重太大，干扰了模型正常的工作过程。当λ取值0.01～0.1时，模型比较稳定，误差也相对较小。

3 结束语

提高推荐预测精度对改善推荐系统的性能具有重要的意义。矩阵分解是预测用户对物品评分的最为常用的方法，它能够很好地解决评分数据稀疏的问题。本文在矩阵分解的基础上考虑了用户的社会属性信息，提出了差值矩阵分解。先按照社会属性将用户进行分组，发现当分组后差值的绝对值|zui|的均值和方差越小，矩阵分解后的精度也就越高。这说明组内用户具有较高的相似度，用户的偏好在该分组上也就越有较强的区分能力。使用用户的年龄+职业进行分组，差值绝对值|zui|的均值和方差最小，取得的精度也是最高的。在MovieLens 1M数据集上对本文提出的方法与主流的算法进行了对比实验，实验结果表明本文方法能有效地提高预测结果的精度。

[1] Lops P, Gemmis M D, Semeraro G. Content-based recommender systems: State of the art and trends[M]// Recommender Systems Handbook. Springer, US, 2011:73-105.

[2] Herlocker J L, Konstan J A, Terveen L G, et al. Evaluating collaborative filtering recommender systems[J]. ACM Transactions on Information Systems(TOIS), 2004,22(1):5-53.

[3] Sarwar B, Karypis G, Konstan J, et al. Item-based collaborative filtering recommendation algorithms[C]// Proceedings of the 10th International Conference on World Wide Web. 2001:285-295.

[4] Simon Funk. Netflix Update: Try This at Home[EB/OL]. http://sifter.org/simon/journal/20061211.html, 2006-12-11.

[5] 项亮. 推荐系统实践[M]. 北京:人民邮电出版社, 2012.

[6] Salakhutdinov R, Mnih A. Probabilistic matrix factorization[C]// Proceedings of the 20th International Conference on Neural Information Processing Systems. 2007:1257-1264.

[7] Salakhutdinov R, Mnih A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo[C]// Proceedings of the 25th International Conference on Machine Learning. 2008:880-887.

[8] Koren Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model[C]// Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2008:426-434.

[9] Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009,42(8):30-37.

[10] Ma Hao, Zhou Dengyong, Liu Chao, et al. Recommender systems with social regularization[C]// Proceedings of the 4th ACM International Conference on Web Search and Web Data Mining. 2011:287-296.

[11] Douban. Douban[EB/OL]. https://www.douban.com/, 2017-07-31.

[12] Trustlet Network Datasets. Epinions [EB/OL]. http://www.trustlet.org/epinions.html, 2017-07-31.

[13] Yang Xiwang, Steck H, Liu Yong. Circle-based recommendation in online social networks[C]// Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2012:1267-1275.

[14] 梅忠,肖如良,张桂刚. 基于受约束偏置的概率矩阵分解算法[J]. 计算机系统应用, 2016,25(5):113-117.

[15] 巫可,战荫伟,李鹰. 融合用户属性的隐语义模型推荐算法[J]. 计算机工程, 2016,42(12):171-175.

[16] GroupLens. MovieLens[EB/OL]. http://grouplens.org/datasets/movielens/, 2017-07-31.

[17] Coveralls. 实现概率矩阵分解和贝叶斯概率矩阵分解代码[EB/OL]. https://coveralls.io/github/chyikwei/recommend?branch=master, 2017-07-31.