水下机器人动力学分析与控制系统研究

王永鼎，董亚龙

（上海海洋大学 工程学院，上海 201306）

0 引言

近年来，随着经济的高速发展，用于水下检测及信息收集的水下机器人的需求不断增加，水下机器人的研究受到广泛关注。无人化、智能化的水下机器人将成为一种趋势，特别是小型水下机器人，研发周期短，机动灵活，成本低廉，常被用于河堤大坝水况监测、河道桥墩水下信息收集，近海码头港口检修以及船舶外体水下检测等，节省了大量的人力物力财力，其市场前景非常广阔，因此对于水下机器人的研究具有重大的理论意义和实际应用意义。

水下机器人由于其强非线性和耦合性，运动参数不确定性以及工作环境复杂，易受外界干扰影响，其要在水下完成指定任务，必须具备良好完善的运动控制系统，这也要求我们首先对水下机器人进行动力学分析。

1 水下机器人坐标系及坐标变换

1.1 建立坐标系

根据国际水池会议推荐和造船与轮机工程学会术语公报体系，参考相关资料[1]，按右手定则建立两个坐标系：静坐标系（E-XYZ）和动坐标系（O-X＇Y＇Z＇），如图1所示。

静坐标系，也称惯性坐标系或地面坐标系，以海面或水面某一点为原点，EX和EY在水平面，EZ正向指向地心。水下机器人的位置和方向描述为分别为水下机器人在静坐标系中的位置，分别为水下机器人对静坐标系的横滚角、纵倾角和艏向角。

动坐标系，也称载体坐标系，以水下机器人的重心为原点，OX＇轴沿水下机器人纵轴方向，正向指向艏部，OY＇垂直于OX＇轴且正向指向右侧，OZ＇垂直于OX＇轴和OY＇轴所在平面且正向指向底部。水下机器人的速度在动坐标系中可描述为速度矢量V=[u v w p q r]T和力（矩）矢量τ=[X Y Z K M N]T。相关参数定义如表1所示。

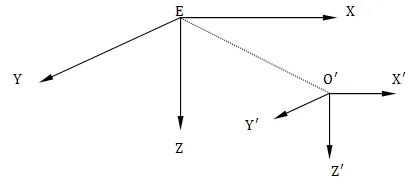
图1 水下机器人坐标系示意图

1.2 坐标变换

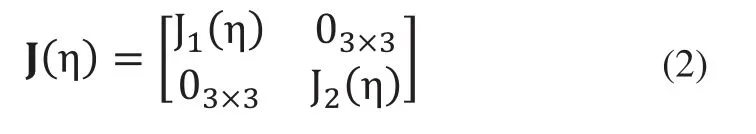
表1 水下机器人参数定义表

式中：

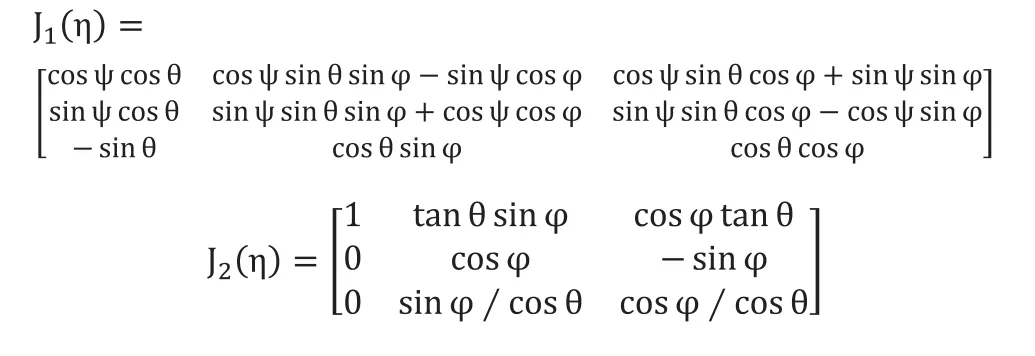
2 空间运动数学模型

水下机器人的运动是一种六自由度的空间运动，可以用动坐标系下的沿三个坐标轴的直线运动和绕三个坐标轴的旋转运动表示[3]。根据刚体牛顿-欧拉方程，六自由度水下机器人在动坐标系中的空间运动方程可描述为[4]：

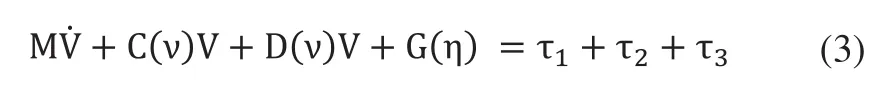
式中，M为包括附加载体的质量MA及惯性矩阵MRB；C(v)为刚体科氏项和离心项矩阵；D(v)为流体阻尼矩阵（水动力损失项）；为重力与浮力矩阵（静力项）；为流体动力和力矩项矩阵；为推进器推力和力矩项矩阵；为水下机器人受到外部扰动产生的力和力矩项矩阵。

水下机器人是一个非线性的动力学系统，其运动规律较为复杂，需要求得的参数较多。而有些参数由于如技术条件、测定环境以及硬件设备等外在条件限制，较难甚至无法测定。为了研究需要，合理地对系统进行适当简化，这里只考虑静力（重力和浮力）、推力和水动力对水下机器人的影响。

2.1 重力、浮力和重力矩、浮力矩

水下机器人受到的重力和在水中受到的浮力作用在同一直线上，重力总是指向地心，浮力与重力方向相反。设重心（xg，yg，zg）与动坐标系坐标原点重合，则这两个力及其力矩可表示为：

2.2 水动力及其力矩

水下机器人在水中受到的水动力主要包括水流阻力和附加质量。水下机器人在水下作加速运动时，对周围的流体会产生作用力，使之产生加速度，克服流体本身惯性需要提供额外的作用力，进而导致水下机器人所受阻力增加，这种阻力增加等同于水下机器人的质量增加，称为附加质量，可由试验求得；水流阻力与水下机器人相对于水流速度的平方成正比。

水下机器人受到的水动力及其力矩可表示为：

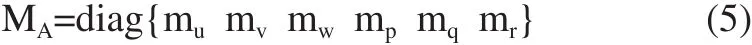
式中，mu、mv、mw分别为沿X＇、Y＇、Z＇轴轴线方向产生的附加质量；mp、mq、mr分别为沿X＇、Y＇、Z＇轴旋转方向产生的附加质量。

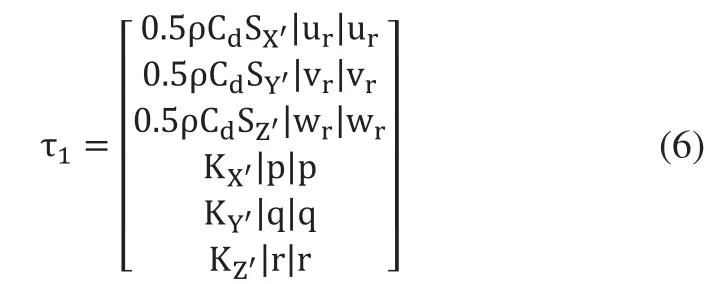
式中，ρ为水密度；Cd为无因次阻力系数，一般通过实验获得，对于大多数水下机器人，一般取0.8～1.0[5]；SX'、SY'、SZ'分别为水下机器人垂直于X＇、Y＇、Z＇轴的横断面面积；（ur、vr、wr）为水流相对于机器人的速度；（KX'、KY'、KZ'）为阻力矩系数，可由试验求得。

2.3 推力及其力矩

水下机器人所受推力及其力矩与推进器的布置、水下机器人的结构、尺寸、线型以及运动要求有关。这里给定推进器的布置，如图2所示。水下机器人在O＇X＇Y＇平面有两个推进器T1、T2，它们相对于X＇轴对称布置，可实现沿X＇轴的平移以及绕Z＇轴的旋转运动；在O＇Y＇Z＇平面有两个推进器T3、T4，它们相对于Y＇轴对称布置，可实现沿Y＇轴的平移以及绕X＇轴的旋转运动；在O＇X＇Z＇平面有两个推进器T5、T6，它们相对于Z＇轴对称布置，可实现沿Z＇轴的平移以及绕Y＇轴的旋转运动；由此，可实现水下机器人进退、潜浮、横移、横摇、纵倾和转艏六个自由度运动。水下机器人主要使用定距螺旋桨，单个定距螺旋桨的推力可由式(7)表示：

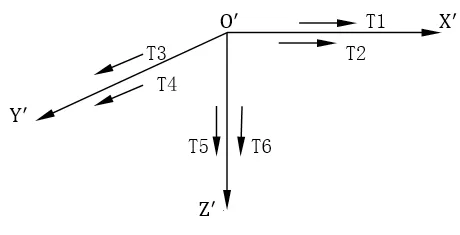
图2 推进器的布置

式中，FTi为第i个推进器产生的推力；ni为第i个推进器的螺旋桨的转速；Di为螺旋桨直径；KTi为第i个推进器的推力系数。

所以，水下机器人推进器推力及其力矩项矩阵可表示为：

式中，RTi为第i个推进器和与之平行的坐标轴的垂直距离。

2.4 建立动力学模型

基于以上受力分析，并对水下机器人水动力学模型适当简化。不考虑水动力损失项及外部干扰力，重心与动坐标系坐标原点重合，即Xg=Yg=Zg=0。可得水下机器人动力学方程：

式中：

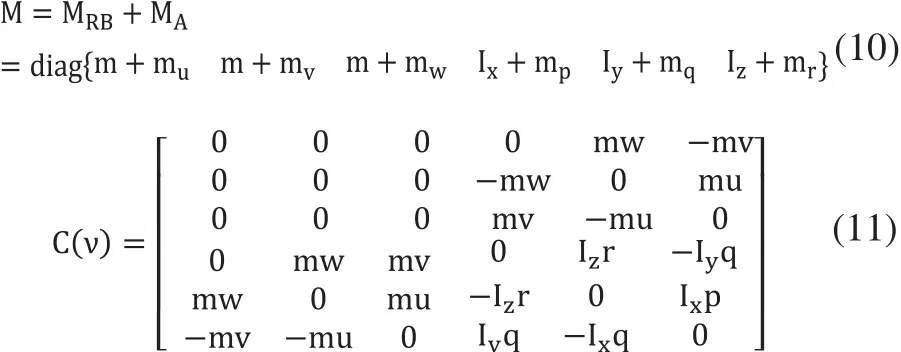
将式(3)～式(8)和式(10)、式(11)代入式(9)，得水下机器人空间动力学方程：

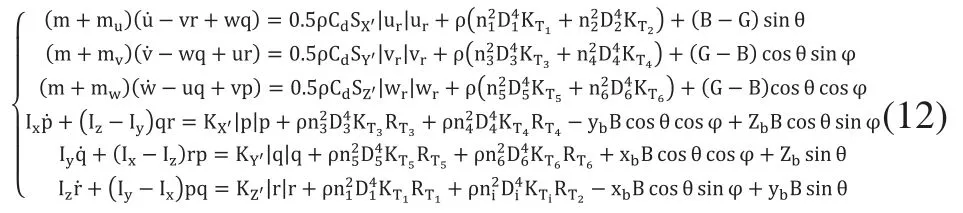
通过以上分析并根据水下机器人的实际情况求解水下机器人动力学方程，可得其在动坐标系下的运动规律（u、v、w、p、q、r），通过坐标转换关系式(1)和式(2)可得其在静坐标系下的运动规律

3 控制系统设计

在以上水下机器人受力分析的基础上，进行水下机器人控制系统研究。水下机器人是一个复杂的非线性系统，通过螺旋桨推进器实现在水中的运动，需要设计合理的控制器进行水下机器人的运动控制，以保证水下机器人在水中运动的平稳性和准确性。以模糊集合论、模糊语言变量和模糊逻辑推理为基础的模糊逻辑控制[6～8]，通过模糊推理和模糊决策实现对复杂系统的控制，具有相当好的鲁棒性、适应性和容错性。模糊控制系统的结构图如图3所示。

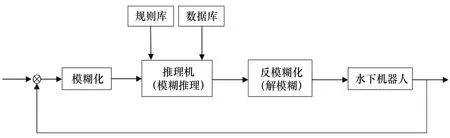
图3 模糊控制系统的结构框图

以水下机器人位置偏差ΔL和速度偏差ΔV作为输入量，以推进器所需提供的推力U作为输出量，对水下机器人进行控制，通过检测装置将机器人的状态反馈到输入端，形成一个闭环反馈系统。其中模糊推力方法可以采用Mandani或Sugeuo两种类型，根据Mandani[9]所提的设计方法，将输入量ΔL、ΔV和输出量U论域范围设定在[-6,6]，将输入量的实际范围离散化，并将其表达成论域区间的变量。模糊化后的输入输出模糊变量集合均为{NB,NM,NS,ZO,PS,PM,PB}，集合中的变量表示{负大，负中，负小，零，正小，正中，正大}。选择三角函数作为输入输出变量的隶属度函数，输入变量ΔV与输出变量U的隶属度函数和输入变量ΔL的隶属度函数一样，如图4所示。

根据水下机器人在水下的状态分析，当水下机器人位置偏差ΔL和速度偏差ΔV均为负大（NB）时，水下机器人偏离目标轨迹并且距离目标轨迹越行越远，此时应调节控制量为正大（PB），纠正水下机器人的实际轨迹，使其向目标轨迹靠拢；当水下机器人位置偏差ΔL为负大（NB），而速度偏差ΔV均为正大（LB）时，水下机器人偏离目标轨迹但距离目标轨迹越行越近，此时将控制量调节为正小（PS），即需要较小的调节量就可以是说下机器人按既定轨迹行进。依此可以得出如表2所示的模糊控制规则表。图5为输入输出的关系三维曲线图。

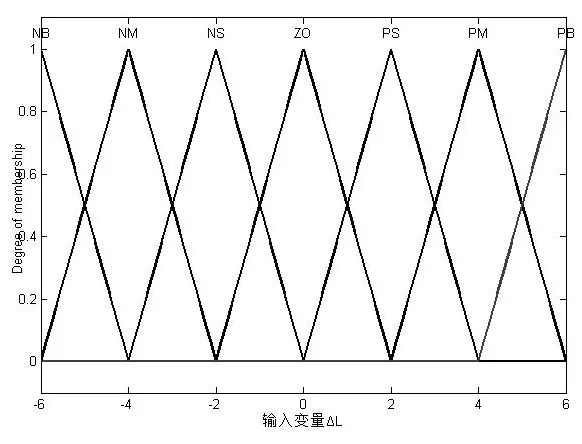
图4 输入变量ΔL的隶属度函数

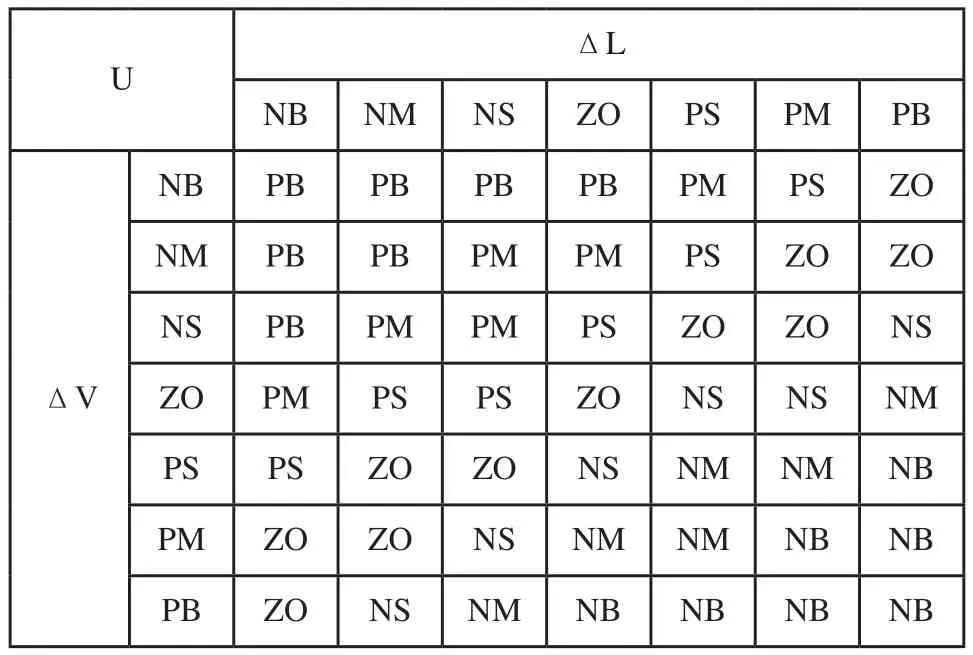
表2 模糊控制规则表

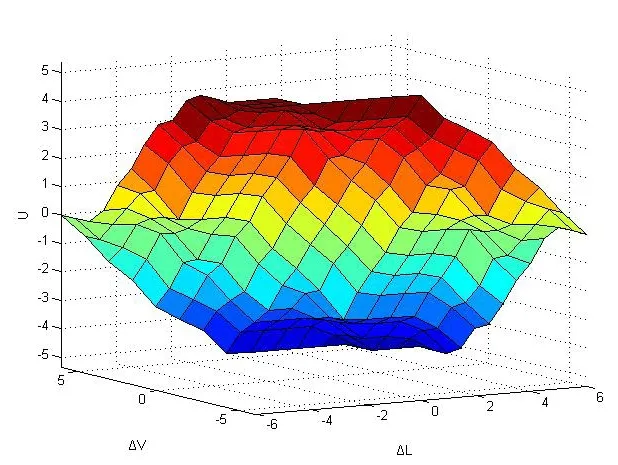
图5 输入输出关系三维曲线图

4 仿真分析

根据以上水下机器人动力学分析以及建立的控制系统，通过MATLAB中的Simulink模块[10]对水下机器人进行仿真实验。水下机器人简化为直径0.2m，长0.4m的均质柱体，且重力、浮力作用可使其保持水平状态，无横倾或纵倾，浮心与重心重合。

设目标在初始位置进行浮潜运动，参考输入深度为4m，水下机器人的预定轨迹依据直接瞄准法[11]进行预设，采样周期0.1s，仿真时长50s。仿真得到水下机器人速度和运动响应曲线，如图6～图8所示。

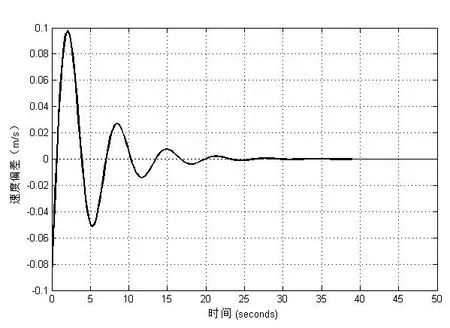
图6 速度偏差曲线

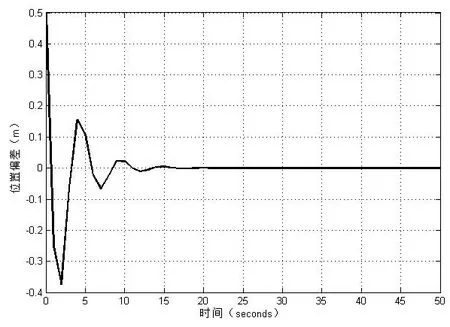
图7 位置偏差曲线

图8 控制变量变化曲线

从图6、图7中可以看出，水下机器人的位置偏差和速度偏差在开始时均有变化，通过控制变量的调节，如图8所示，在t=15s时，它们的曲线趋近平稳最终趋向于零，表明水下机器人的实际轨迹最终趋向于理论轨迹，速度趋于稳定，系统最终稳定，并经多次仿真，得到具有类似的结果，即在经历开始变化后，通过控制变量的调节，系统最终稳定。仿真结果表明，该控制方法可

【】【】

行，能够使水下机器人在运动过程中保证其稳定性与准确性。

5 结束语

水下机器人的运动控制技术是机器人智能化的核心之一，动力学分析是研究运动控制的基础。本文首先建立了水下机器人坐标系，对水下机器人进行了动力学分析，其次建立了水下机器人6自由度运动学模型，描述了水下机器人的运动规律，最后设计了一种水下机器人模糊逻辑控制器，并通过计算机仿真实验验证了控制算法的正确性和有效性。从仿真结果来看，设计的控制器使水下机器人具有了较好的适应性和稳定性，进而验证了动力学模型的正确性以及控制方法的可行性，同时也为水下机器人水下相关运动的研究奠定了基础。

[1]廖华丽,蔡庆安,徐卫,刘晓磊.自治水下机器人运动控制的动力学分析[J].机电一体化,2008,(3):58-60,63.

[2]朱大奇,胡震.水下机器人故障诊断与容错控制技术[M].北京:国防工业出版社,2012.2:39-40.

[3]蒋新松,封锡盛,王棣棠.水下机器人[M].沈阳:辽宁科学技术出版社,2000:12-17.

[4]De Souza, E.C. Maruyama, N..Intelligent UUVs: Some issues on ROV dynamic positioning[J].IEEE transactions on aerospace and electronic systems,2007,43(1):214-226.

[5]边宇枢,高志慧,贠超.6自由度水下机器人动力学分析与运动控制[J].机械工程学报,2007,43(7):87-92.

[6]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[7]Cang Ye Yung, N.H.C. Danwei Wang.A fuzzy controller with supervised learning assisted reinforcement learning algorithm for obstacle avoidance[J].Systems, Man and Cybernetics, Part B,IEEE Transactions on,2003,33(1):17-27.

[8]Yang, S.X. Hao Li Meng, M.Q.-H. Liu, P.X..An embedded fuzzy controller for a behavior- based mobile robot with guaranteed performance[J].Fuzzy Systems, IEEE Transactions on,2004,12(4):436-446.

[9]Mandani, E, H, Assilian, S.An experiment in linguistic synthesis with a fuzzy logic controller[J].International Journal of Man-Machine Studies,1975,1(7):1-13.

[10]黄忠霖,黄京.控制系统MATLAB计算及仿真[M].北京:国防工业出版社,2009:105-110.

[11]《鱼雷力学》编著组.鱼雷力学[M].北京:国防工业出版社,1992.