基于模态分析的纯电动垃圾车车架拓扑优化

袁 敏，骆 静，徐一心，唐克岩

（成都理工大学 工程技术学院，乐山 614004）

0 引言

纯电动垃圾车每天的作业任务和行驶里程相对固定，受续航里程的限制相对较小，因此越来越多地应用在城市中。现阶段纯电动汽车用动力电池的技术很难有一个较大的突破，要增加续驶里程更多的是进行轻量化。车架占纯电动垃圾车质量比重大，因此选取车架作为轻量化的具体对象。传统的轻量化多凭经验，经轻量化后的车架动静态特性往往达不到汽车行驶要求。因此，本文引入拓扑优化技术进行车架设计，以使设计的车架能满足动静态特性。

1 理论基础

1.1 模态分析理论

模态频率、阻尼比和各阶振型是表征车架动态特性的主要参数。模态分析求解的基本方程实质上即经典的特征值问题求解。可用如下的方程式进行描述：

ωi为第i阶模态的固有频率；

[M]为质量矩阵。

为研究车架结构动态特性，本文引入模态参数识别来分析车架的模态特征，作为判断车架设计合理性的客观依据，进而为改进车架结构设计提供相关参数。

1.2 拓扑优化理论

分析最优传力结构和给出最佳材料分布方案是拓扑优化的核心任务，是和传统经验设计的最主要区别。以使分析出的结构可以同时满足给定的约束条件和目标函数。采用主流分析软件Ansys完成拓扑优化。设计变量是各单元密度大小，从0到1连续变化；目标函数根据设计要求选择，常用结构柔度或者模态频率。

结合本文的具体设计，车架拓扑优化数学模型可以描述为：

式中：f为车架固有频率；

µi为第i个单元的伪密度，

α为体积去除比；

V为优化前的设计空间体积。

2 准备工作

2.1 设计空间的建立

为在Ansys中完成有限元计算，在三维建模软件中完成了车架的数字模型建立。在三维软件中建立的有限元模型一般不能直接和有限元软件Ansys进行数据交换。因此，需要将三维设计空间模型转换为通用格式，再将通用格式文件导入Ansys。车架材料选用16Mn，其材料属性如表1所示。

表1 16Mn材料属性

导入有限元软件中的设计空间模型是一个连续体结构，因此首先要将设计空间网格化以离散为有限元结构。网格化前需选择相应的单元类型，要在Ansys中实现拓扑优化功能，必须选择对应的单元类型。根据车架具体结构，为简化计算，选择三维实体单元来进行网格划分。有限元软件中预设了多种三维实体单元类型，但是要进行拓扑优化必须选择SOLID92和SOLID95。

建立的车架设计空间并不是所有结构都要进行拓扑优化，根据车架结构，两纵梁间的实体单元被设为优化区域，具体包括横梁和车架中部的电池安装托架，单元类型编号设为1，设置好相应的目标函数后即执行拓扑优化运算；纵梁作为不可优化区域，单元类型编号设定为≥2，在拓扑过程中不进行迭代计算。图1为在Ansys中建立的车架设计空间有限元模型。

图1 车架设计空间有限元模型

2.2 模态分析

车架主要受到低阶模态的影响，因此本文提取车架设计空间的前6阶模态(不含刚体模态)。将通过Ansys计算得到的数据绘制成模态频率曲线如图2所示。

图2 模态频率

各阶模态振型图如图3所示。

图3 各阶模态振型

第1阶振型为一阶垂向弯曲，车架前部后部振幅较大；第2阶振型为二阶垂向弯曲；第3阶振型为一阶扭弯振动，最大振幅出现在车架两纵梁前后端；第4阶振型是局部振型，主要是车架前段和后段的局部一阶扭转振动；第5阶振型为三阶垂向弯曲；第6阶振型为整体二阶扭转振动。最大振幅发生在第3阶的车架前段，最大值0.056，所以前横梁为整个车架的薄弱之处，在工作中易发生扭转振动。虽然第1阶的最大振幅在前六阶中最小，但由于其模态频率相对较低，最易发生共振，也是车架的动态薄弱环节。

3 拓扑优化

为进行拓扑优化，除刚体模态外的车架1阶模态频率最大化被设置成优化目标。除此外，还需初步给定设计空间的体积去除百分比。在15次迭代运算后，优化过程结束。通过后处理，在Ansys中绘出结果云图如图4所示以及相应的计算迭代过程如图5所示。

图4 伪密度云图

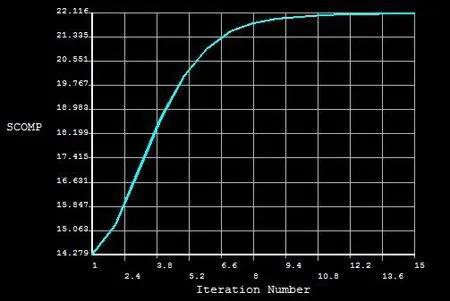
图5 迭代曲线

由拓扑优化云图分析可知，车架的拓扑形状规则，拓扑结果边界比较清晰，有利于下一阶段的给出具体的优化结构。第15次迭代运算后拓扑优化过程结束，由图5曲线可知结算结果收敛有效；经过计算，1阶模态频率从优化前的12.103Hz增加到优化后的22.116Hz，有了明显的提高。

4 二次设计

图4中的云图为设计人员提供了初步的设计概念，但还不是最终的具体结构设计。还需根据以上的拓扑计算结果，基于车架设计空间二次设计，以得到车架具体结构。

对二次设计的车架进行模态分析，参数设置和优化前相同，得到前6阶模态频率如图6所示。1阶模态汽车性能影响最大，由图可知二次设计的车架1阶频率为24Hz。对于纯电动垃圾汽车来说，其激励输入主要来自路面、驱动电机和传动轴。城市路面上激励频率一般低于20Hz；驱动电机的激励频率为30～50Hz；传动轴的不平衡引起的振动的频率大于30Hz。由此可知，二次设计的车架1阶频率低于驱动电机激励频率和传动轴不平衡振动频率，而高于路面激励频率，即二次设计后的车架整体模态避开了纯电动垃圾车常用工作频率范围，所以其动态特性符合工作要求。

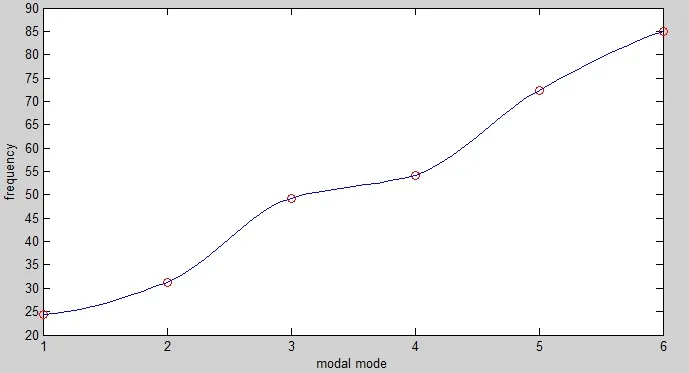
图6 模态频率

5 结论

1）经过模态分析得到了车架的前6阶模态频率，根据模态分析结果分析得到了车架的动态薄弱环节，这些薄弱环节是拓扑优化的依据。

2）将车架的第1阶模态频率的最大化设为优化目标，通过迭代计算得到了有效的拓扑优化结果。

3）根据拓扑优化结果进行了二次设计，并对二次设计后的车架进行了模态分析，分析结果表明二次设计后的车架1阶模态频率显著提高，满足动态特性要求。

4）目前国内针对纯电动垃圾车专用底盘的研究开发还不多见，本文引入拓扑优化方法进行车架结构设计，车架结构得到轻量化优化的同时还大大提高了设计效率。

[1]袁敏,陈翀.飞机除冰车专用车架拓扑优化及强度分析[J].制造业自动化,2013,35(3):127-129.

[2]闫成,高翔.履带车辆车架的优化设计[J].机械设计与制造,2014(10):19-22.

[3]陈安涛.6×6型越野汽车车架的拓扑优化[D].哈尔滨工业大学,2008.

[4]庄毅胜,黄妙华.基于拓扑优化的电动游览车车身优化设计[J].轻型汽车技术,2009(Z3):10-14.

[5]张心光,高宾.基于不同工况下的FSC赛车车架有限元分析[J].制造业自动化,2015(19):44-46.

[6]于玉真,李志斌. 微型电动车车架结构优化设计与分析[J]. 制造业自动化,2015(2):135-138.

[7]盛建,戴作强.纯电动客车车架结构模态分析与优化设计[J].制造业自动化,2015(15):44-47.

[8]杨良勇,成传胜.基于有限元技术的某微型车转向支架拓扑优化的研究[J].组合机床与自动化加工技术,2011(9):88-91.

[9]曾发林,李德华.某车架有限元建模及仿真研究[J].制造业自动化,2012,34(3):103-106.

[10]袁敏.牵引式升降转运平台有限元分析及拓扑优化[D].西华大学.2014.