基于四旋翼无人机的二阶PD积分滑模控制算法研究
陈洪楷,满 红,余义斌
(五邑大学 信息工程学院,江门 529030)
0 引言
近年来,由于四旋翼无人机能够替代人类完成危险系数高、工作量大及操作困难等任务,被广泛应用于质量安全检测、生命探测、城市安防、物流快递业务等场合,对其控制方法的研究也备受关注。
A moozgar M H等人使用模糊控制规则实时调整PID控制参数[1],但是规则的划分具有一定的不确定性,因而影响了控制精度。赵振宇利用神经网络逼近飞行系统的不确定性,结合滑模控制可以有效减小系统的跟踪误差[2],但是存在复杂非线性导致神经网络计算量剧增实现困难的问题。Rong Xu等人将四旋翼无人机系统分成全驱动子系统和欠驱动子系统[3],在全驱动子系统却采用常规的PD控制算法难以保证系统的控制精度和鲁棒性。刘凯悦等人利用单位四元数法描述系统姿态,设计了反演滑模控制器得到良好的轨迹跟踪效果[4],但忽略了滑模控制抖振问题。因此,寻求一种抑制滑模控制抖振的方法是提高无人机飞行稳定收敛速度的关键[5]。
本文利用参考文献[6,7]给出的四旋翼无人机简化动力学模型,外环利用二阶PD算法推算出控制律和内环控制信号,内环使用饱和函数替代切换函数,通过积分滑模控制器所接收外环的控制信号得出内环的控制律。这样可以有效抑制抖振效应,提高无人机飞行稳定的收敛速度和跟踪精度[1]。
1 四旋翼无人机的数学模型描述
四旋翼无人机简化结构如图1所示,机体中心为无人机的控制中心,四个旋翼由机臂末端的直流无刷电机驱动,相邻两个电机旋转的方向相反,主要是用来平衡飞行器的总角动量防止机身失衡而发生翻转。另外,还包括两个主要的坐标系:地面惯性坐标系;依附于飞行器的机体坐标系。

图1 四旋翼无人机简化结构图
假设忽略微小的空气动力学效应,四旋翼无人机的数学模型如下[6,7]:

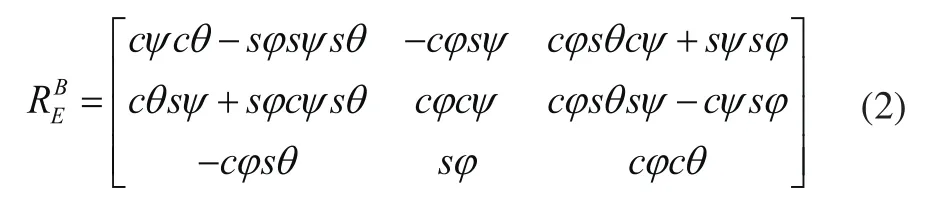
在图1中,通过对电机2和电机4所施加的推力大小
不同使机体绕着b1轴旋转,产生的角度为俯仰角θ;对电机1和电机3的推力大小差异使机体绕着b2轴旋转,产生的角度为滚转角ϕ;通过电动机转矩来改变施加在机体上的阻力矩来实现围绕轴线b3的旋转,产生的角度为偏航角ψ。
角速度矢量[p q r]T与惯性坐标系下姿态角之间的转化关系如下所示:

2 二阶PD积分滑模控制控制器的设计
根据所提算法的思想,设计四旋翼无人机二阶PD积分滑模控制器结构如图2所示。

图2 控制器结构图
位置控制环处于外环,其中位置子系统控制器接收反馈回来的实际轨迹和航迹指令信号的期望轨迹,利用两者的偏差,使用二阶PD算法得到外环控制律u1以及姿态控制信号。内环姿态环接收姿态控制信号以及反馈回来的实际姿态信号后,利用两者的偏差,在姿态子系统控制器使用积分滑模控制得到内环控制律u2。
2.1 位置环二阶PD控制器设计
令期望轨迹为ξd,它由三个位置向量和一个滚转角组成:

位置环控制信号为:

实际轨迹为:
其中:
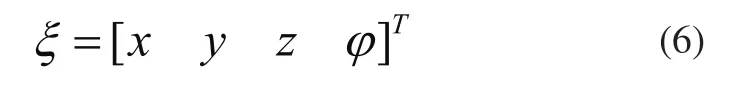
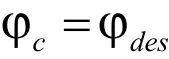

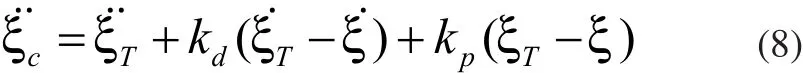
由式(1)~式(6),推导得到控制信号加速度矢量与控制律u1的关系如下:
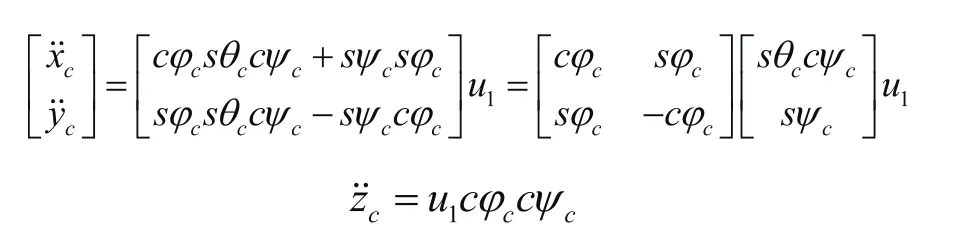

由式(9)可得:

则:

由式(8)可得:

为了防止式(11)左边值超出[-1,+1],而造成θc不存在,用分段取值的思想来解决这个问题:令。

结合式(2)、式(5)、式(8)、式(10)、式(12),可以推导得到外环控制律u1:

2.2 姿态环滑模控制器设计

即:

令:
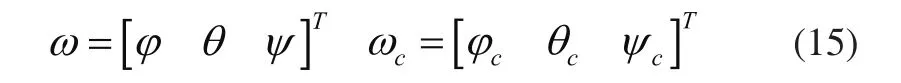

由式(14)和式(15)得到其一阶微分:

其中:

趋近律v选择指数趋近律,令:

其中,K是滑模等速趋近律的增益矩阵,ε是指数趋近律的增益矩阵,K>0,ε>0。
为抑制滑模控制的抖振效应,引入了积分滑模控制和指数趋近律之后,用饱和函数项代替切换函数:

,则:


综合以上的分析,将式(14)、式(15)、式(16)代入式(19),得到内环控制律u2为:
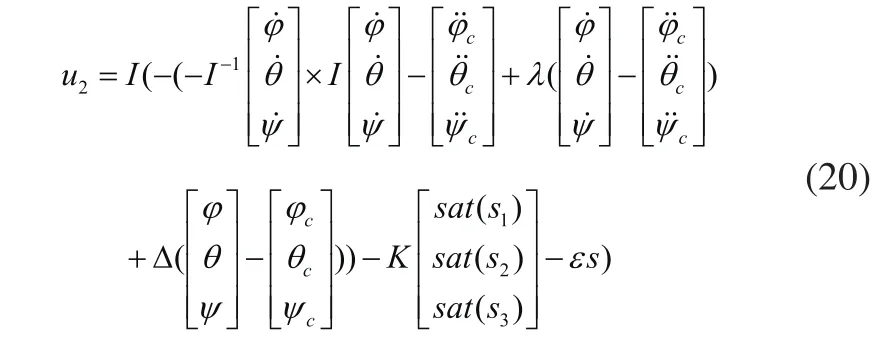
其中:

3 仿真分析
为验证所提算法的有效性,现假设从有、无干扰两个方面对无人机能否快速跟踪给定轨迹展开仿真研究。其中,采用的干扰模型可以模拟实际风干扰,其速度模型如下[8]:

仿真所需的四旋翼系统参数如表1所示。

表1 四旋翼系统参数
仿真各参数设置如下:
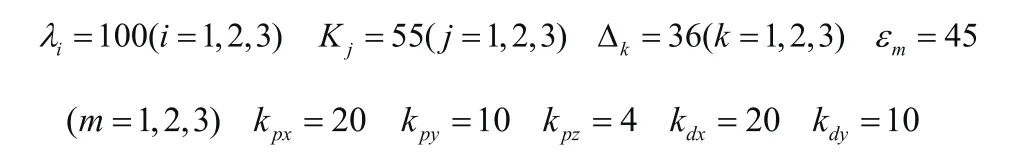
当系统没有受到扰动情况下,图3至图6分别给出仿真结果。图3是给定的规划航迹图,图4是无扰动下的控制器输出波形,图5是各轴方向上矢量运动和姿态角随时间变化的波形,从图形中可以看出实际值和参考值的吻合程度很高,图6是系统变量误差变化曲线,可以看出误差波动的范围较小。

图3 规划航迹

图4 无扰动下的控制器信号输出
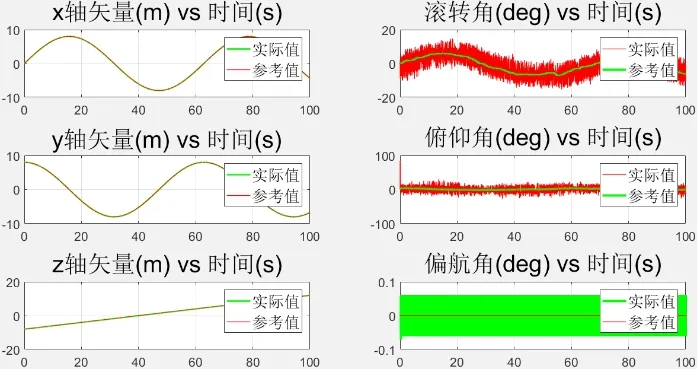
图5 各轴方向运动和姿态角变化

图6 各轴方向误差和滚转角误差
假设系统在t=25s时加入风干扰,仿真结果如图7到图10所示。从下图中可以看出当系统受到干扰时,波形和飞行轨迹都发生了跳变,大约经过5s后波形和轨迹可以恢复正常状态。

图7 干扰下飞行轨迹图

图8 干扰下控制器输出
【】【】

图9 干扰下各轴矢量运动和姿态角变化

图10 干扰下各轴方向误差和滚转角误差
从图4和图8的仿真结果可以看出,使用饱和函数的积分滑模控制控制量u2的各个分量无论有无干扰都能保持在-0.02到0.02的幅值之间抖动,有效地抑制了滑模控制本身的抖振。综合分析以上仿真结果,可以看出所设计的控制算法能够应对突发干扰,使无人机可以快速收敛到预定的轨迹,同时也抑制了滑模控制带来的抖振现象,验证了所提方法的可行性和有效性。
4 结论
四旋翼无人机是具有6个输出和4个输入的欠驱动系统,为获得更好的飞行稳定的收敛速度,将整个系统分成外环的位置控制系统和内环的姿态控制系统,外环采用二阶PD算法,内环利用抑制抖振的饱和函数项的积分滑模控制算法。在有干扰和没有干扰的情况下进行仿真实验,验证了所设计的控制器能够使无人机有较好的跟踪性能和收敛速度,说明所提算法具有较好的鲁棒性和可行性。
[1]A moozgar M H,Chamseddine A,Zhang Y.Fault-tolerant fuzzy gain-scheduled PID for a quadrotor helicopter testbed in the presence of actuator faults[A].IFAC Conference on Advances in PID Control[C].Brescia,Italy,2012.
[2]赵振宇,卢广山.具有未知干扰的无人机鲁棒滑模飞行控制[J].计算机仿真,2012,29(2):63-67.
[3]Rong Xu and U mit O zgu ner. Sliding Mode Control of a Quadrotor Helicopter[A].Pr-oceedings of the 45th IEEE Conference on Decision & Control[C].Manchester Grand Hy-att Hotel San Diego, CA,USA,December 13-15,2006:4957-4962.
[4]刘凯悦,冷建伟.基于滑模控制的四旋翼无人机的轨迹跟踪控制[J].天津理工大学学报,33(2):60-64.
[5]陈志梅,王贞艳,张井岗.滑模变结构控制理论及应用[M].电子工业出版社,2012.8.
[6]Robert Mahony,Vijay Kumar, Peter Corke.Modeling,Estimation,and Control of Quadrotor[Z].Digital Object Identif ier 10.1109/MRA.2012.2206474,2012,7.
[7]Bambang SUMANTRI, Naoki UCHIYAMA, Shigenori SANO,Yuma KAWABATA. Robust Tracking Control of a Quad-Rotor Helicopter Utilizing Sliding Mode Control with a Nonlinear Sliding Surface[J].Journal of System Design and Dynamics,2013,7(2):226-241.
[8]Oualid Araar, Nabil Aouf. Quadrotor Control for Trajectory Tracking in Presence of Wind Disturbances[A].2014 U KACC International Conference on Control[C].Loughborough,U.K,2014,7.

