在小学数学课堂中渗透“有限思想与无限思想”
广东省清远连州市连州镇实验小学 赖卫轻
我们经常说自己渺小的像一粒沙子,一粒沙子是有限的,沙滩的沙子是无限的,无限的沙子里包含着一粒粒沙子;一滴水、一桶水、一池水是有限的,一片汪洋是无限的,汪洋大海中能取出有限的一滴水、一桶水……茫茫宇宙有无限大,浩浩星际无限多,千百年来,“有限与无限”是一个古老而又常新的永恒哲学问题,有限与无限这两者间既有区别,又有联系,而且在一定条件下可以相互转化。以下就从几个方面探究如何在数学教学中渗透有限与无限的思想。
一、在概念教学中渗透有限思想和无限思想
数学教学的具体任务之一——数学概念是数学知识体系的“细胞”,是建立数学理论的基础。正确理解、掌握和运用数学概念是学好数学理论的前提。数学概念的教学是一项非常重要的任务,在数学概念的教学中渗透有限思想和无限思想,数学是思维的科学,概念是思维的细胞,教好概念是教好数学的内在要求。概念教学搞不好,数学课程目标的实现就失去了根基。因此,我们必须重视数学概念的教学。
二、在计算教学中渗透有限思想和无限思想
在计算教学中,我们往往不会直接点明所应用的数学思想方法,但是我们在教学中已经不经意地渗透了迁移、推理、符号化、有限和无限的数学思想。如在教学《能除得尽吗》这一课时,我出示情境图:

然后问:“你们从图中获得了什么信息?能提出一个数学问题吗?”生:“蜘蛛3分钟爬行73米,蜗牛11分钟爬行9.4米,它们谁爬行得快?”我继续追问:“如何可以知道它们谁爬行得快?怎样列式?”学生回答:“可以比较它们的速度。”还有学生答:“蜘蛛的速度可以用73÷3来计算,蜗牛的速度可以用9.4÷11来计算。”
蜘蛛和蜗牛平均每分钟爬行多少米?
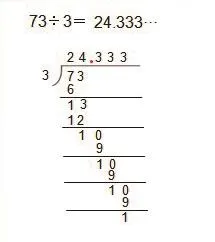

根据展示的学生计算过程,引导学生思考:①通过计算,你发现什么问题?②这两道题里,商的小数部分和余数有什么特点?③你们如何表示这样的商?学生小组讨论后汇报:“我们发现怎么除也除不尽,73÷3的余数始终是1,商始终是商3,是无限重复。”我再问:“那你们这道题的商的横式是怎么写的?为什么写省略号?小数部分重复出现的数字应写几个?”学生回答:“写省略号表示除不尽;重复数字我们认为写2个比较合适,因为写少了,不能表示依次重复出现的特点,写多了麻烦,也没有必要。”我再引导学生观察这两个商,想一想:这两道题和我们前面的计算题有什么不同?前面的计算题都能算得完,这两道题除不尽,这两道题的商中有数字依次重复出现。最后做出小结:像24.33…、0.85454…等都是无限循环小数。
三、在公式教学中渗透有限思想和无限思想
公式教学在数学教学中非常重要,在公式的教学中经常由抽象到直观,有数学的模型思想,有转化的数学思想,还有有限与无限数学思想。如圆的面积,只要给定了一个半径为定长的圆,无论这个圆的半径有多大,它的面积总是有限的,在推导面积公式的过程中,通过把圆划分成无限个全等的扇形,利用这些扇形组成一个近似的长方形,转化成长方形的面积来计算出面积。
数学思想是数学方法的进一步提炼和概括,数学思想的抽象概括程度高一些,而数学方法的操作性更强一些,所以数学思想方法是数学的灵魂。有限与无限的数学思想除了可以在上述几种情况中渗透,还有角的边、平行线、数的认识、直角、平角、周角等数学教学中也可以不断渗透和提升,数学思想的研究之路艰难崎岖,需要我们不停摸索探究,我们需要用数学思想的明灯指引数学教学之路走得更远、更高。

