计及网损的快速经济调度方法

李本新，韩学山，蒋哲，李文博



计及网损的快速经济调度方法

李本新1，韩学山1，蒋哲2，李文博2

（1．电网智能化调度与控制教育部重点实验室(山东大学)，山东省 济南市 250061；2．国网山东省电力公司电力科学研究院，山东省 济南市 250003）

若网损近似为常数，对机组费用曲线满足凸特性的经济调度可解析求解，而网损实际是随机组功率变动而变动的，使这一解析求解的方法不能直接使用。对此，借助网损与机组功率间存在的线性凸特性的规律，依据潮流方程，提出网损随机组功率变动的快速经济调度算法，该算法将网损变动的经济调度问题转化成网损不变经济调度可解析的序列组合，使其在单调有限次代数计算后获得经济调度最优解。

电力系统；经济调度；网损；凸特性

0 引言

因输配电引起的网损是衡量电力系统运行质量的一个重要的经济指标。发电与用电在位置上的差异性越大，网损也就越大，同时，网损也与机组的运行方式有紧密的关系。随着电网规模的快速发展，加之节能减排、环境保护等政策驱使，在调度中如何减少网损是电网实现节能的重要指标之一，这是电力系统经济调度的基础问题[1-7]。

早在20世纪30年代，经济调度问题就得到研究和应用，提出了以等耗量微增率准则为核心的系列有效方法[8-11]。2000年，文献[12]对不计及网损随机组功率变动的经济调度给出解析论证，提出满足一定条件且符合实际的解析方法。在计及电网网损随机组功率变动时，文献[12]的方法能否继续得到直接或间接使用，这便是本文要探索的问题。

网损随机组功率变动的经济调度一直是一个复杂的优化难题，对此，学者们进行了诸多探 索[13-18]，如系数法、阻抗矩阵法、基于雅克比矩阵转置方法，这些方法要么是统计意义下网损表达的近似，要么需要一定的模型简化和近似。若要精准的表达网损与经济调度间的关系，就必须用最优潮流的概念，这使得经济调度问题趋于复杂化，无法快速进行求解。关于如何折中处理经济调度与网损之间的关系，2005年，文[19]从潮流概念出发，对网损与节点注入量间关系展开深刻的理论分析，给出网损可以表达为潮流注入量(节点注入功率，节点电压)的支撑线性超平面，且当满足一定条件时，对已确定的超平面随潮流注入量的变化满足凸特性，从而使网损可以表达为控制量的线性函数，为网损随机组功率变动经济调度的简单求解提供了重要基础。

在此基础上，本文提出一种网损随机组功率变动的经济调度序列解析的快速求解方法，该方法在文献[12]思想的基础上，结合文献[19]的理念，给出序列的单调解析流程，依据解析的经济调度方法和潮流解的副产品可快速寻求网损变动的经济调度的最优解。这对当今量测全景化、广域化的能源互联网概念的提出和应用而言，有着更为积极的意义。

1 问题描述

经济调度问题一般可以描述为如下形式：

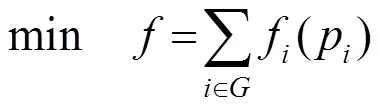
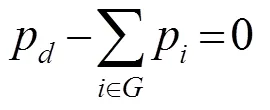
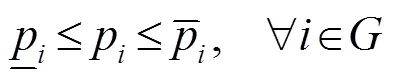
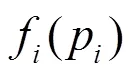
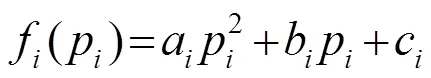
式中：a、b、c分别为机组的成本特性常数，该特性为严格的凸函数。

式(2)为发电与负荷平衡约束，其中

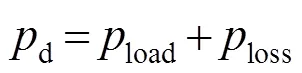
式中：load为负荷需求；loss为对应的电网网损功率。

上述问题就是一般的经济调度，从对偶优化数学角度讲，该问题属于原问题。当不考虑网损随机组功率变动时，网损一般设为常数；当考虑网损随机组功率变动时，必须引入相应潮流方程，建立网损随机组功率的变动规律。

2 网损不变的经济调度

当假设网损为常数时，借鉴文献[12]求解思路，根据对偶原理，有拉格朗日增广目标函数：

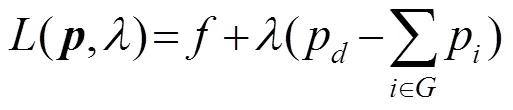
式(6)中：为机组输出功率列向量；为拉格朗日乘子。从而，原问题的对偶问题可以表示为

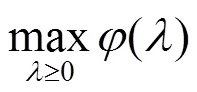
式中

式中

可见，给定下，由式(10)可决策各发电机组输出功率的最优值，表示如下：

由于原问题为凸规划问题，当对偶问题取得最优解(*)时，相应的机组输出功率也为原问题的最优解，且满足：

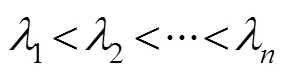
在上述假设下，定义()如下：

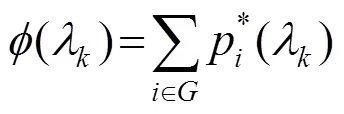
可见，()为关于的分段线性递增函数。

分析可知，在式(13)序列中，若(1)>p或()<p，则上述经济调度问题无解；否则，存在*使(*)=p的最优解；若最优解存在，依据 式(14)，依次按=1,2,¼,，其中()³p是终止分点，则有如下序列计算：

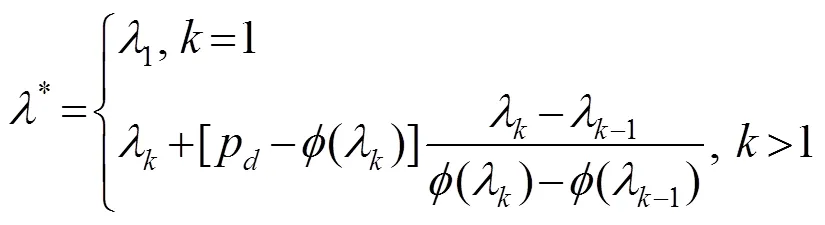
由式(15)，计算*，并代入式(11)，即依次得各发电机组最优输出功率，从而完成经济调度问题解析求解。

3 网损的变动规律

本文在纯有功模式下，研究网损随机组功率变动规律，即认为电网有足够的调控能力使各节点电压幅值保持恒定，从而使潮流方程近似为 全节点潮流，该潮流方程(直角坐标)可抽象表示为

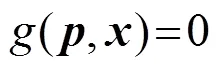
式中：为状态变量列向量(直角坐标形式下节点电压实部和虚部)；为控制变量(机组输出功率)，其他参量隐含其中。

由文[19]可知，在一定状态下(如0、0)，假设网损对控制变量的灵敏度为，围绕给定状态，当发生任意扰动时，网损随机组功率变动有如下规律：

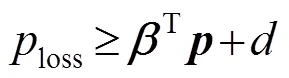
式中为与控制变量无关项，在本文研究过程中为常数。特别地，当=0时，式(17)变为等式，其他则为严格不等式。

由式(17)可见，作为潮流解的副产品构成网损与机组功率间关系的纽带，为简捷有效对网损随机组功率变动的经济调度问题求解提供了重要的基础。

4 网损随机组功率变动的经济调度

按式(17)，在计及网损随机组功率变动时，原问题的机组发电与负荷平衡约束(见式(2))可以表示为

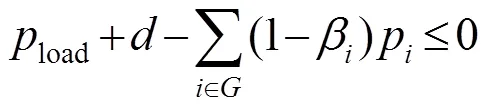
网损变动时，式(9)可改写为

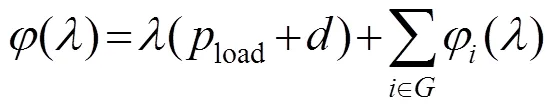
式中

相应地，给定下，各发电机组输出功率的最优值修正为

由式(21)可见，分点集元素修正为各发电机组允许输出功率最小、最大值对应的边际成本与网损惩罚项1/(1-b)的乘积。

模型修正后，原问题依然满足凸优化条件，损耗为常数的经济调度方法仍然适用，相应地，式(12)、式(14)分别修正为：

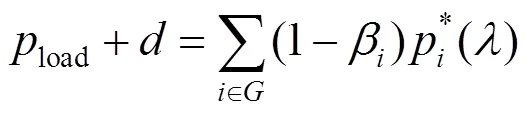
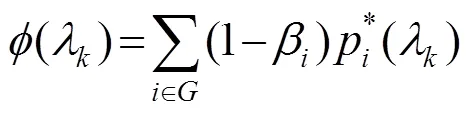
若设d=load+，则按由式(15)构成的序列，计算*，并代入式(21)，即得各发电机组输出功率，从而完成一次损耗变动后经济调度问题的解析求解。

分析可知，网损随机组功率变动的经济调度模型中，来源于电网络潮流方程，反映了网损产生的物理规律，同时又是协调方程引导下寻求经济最优机组功率分配(见式(21))关键而核心的参数，当协调方程引导下的机组功率偏离对应潮流状态时，将导致式(18)中预估的网损低于实际值，使决策的机组功率在实际中无法直接执行，为此，需依据潮流方程，对其中的平衡机组增加功率输出以满足有功平衡。按上述处理后，式(18)所示的不等式约束将变为严格不等，机组功率分配的最优性条件(协调方程)亦难以满足。反之，当β对应潮流状态与决策的机组功率是一致时，即，该机组功率既满足协调方程引导下经济最优，又满足负荷潮流方程引导下的网损的物理规律，这一情景下，式(18)的不等式约束将转化为等式，所得的机组功率亦满足最优性条件。由此，利用上述关系用于网损随机组功率变动的经济调度问题求解，核心在于寻求与潮流状态相匹配的最优调度解，就具体流程而言，一是在凸特性条件满足范围内，寻求机组向最优调度解逼近的机组功率变动方向，二是在每一次变动过程中经济调度可显式、解析的求解，但寻求这一解序列的单调性是十分重要的。在这一序列中，每一次优化解对应的发电费用的变化趋势反映了解序列的特性，可将其作为判断机组输出功率是否修正的依据，这就保证了求解序列的单调性。

按上述，促使解序列单调的修正方程可表 达为

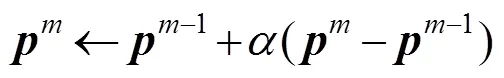
式中：-1、分别为对应-1和次序列解析的优化解；为限制满足凸特性、单调性的步长，范围为[0, 1]。

5 计算流程

网损随机组功率变动的经济调度的计算流程可按如下步骤执行：

1）网损不变的经济调度或寻求电网大数据系统中与当前状态相近的进行网损随机组功率变动的经济调度，得出机组输出功率值。

2）用机组输出功率值进行潮流计算，修正平衡机组输出功率，在此基础上计算及发电费用。

3）更新式(18)，进行网损随机组功率变动的经济调度，得出机组输出功率。

4）进行潮流计算，修正平衡机组输出功率，并计算及发电费用。

5）校验发电费用是否单调递减，如单调递减，转入步骤6）；否则，按式(24)修正机组输出功率，返回步骤4）。

6）校验是否满足式(25)所示收敛准则，如满足，则计算结束，输出结果，否则返回步骤3）。

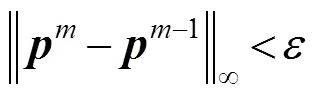
6 算例分析

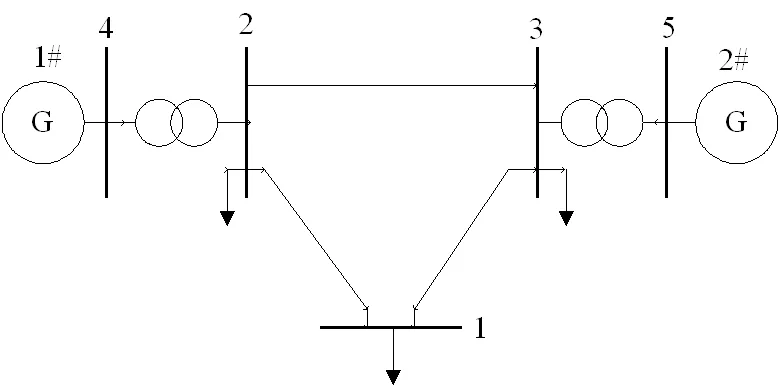
图1 IEEE-5系统结构图

表1 发电机组相关特性参数

表2 负荷相关特性参数(标幺值)

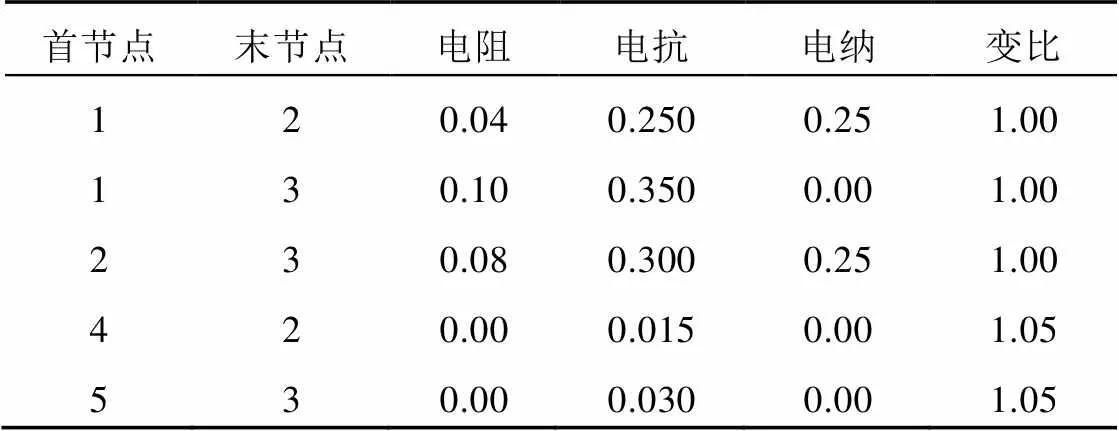
表3 电网元件参数(标幺值)

为了验证式(18)反映的规律，利用本文方法对上述算例系统进行测试，并给出计算结果，如表4所示。

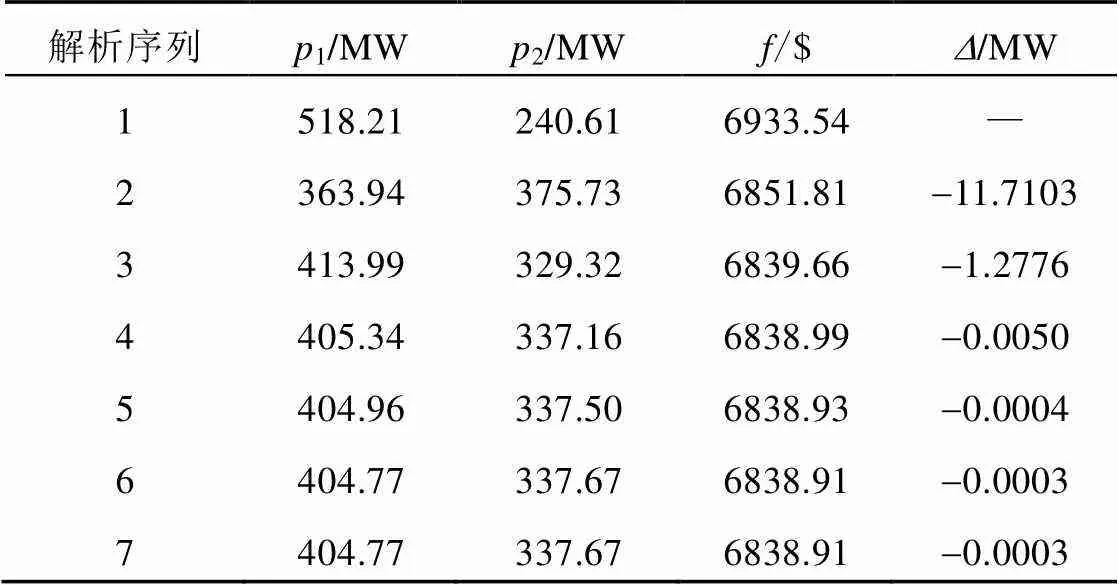
表4 最优状态临近迭代过程(a=0.5)

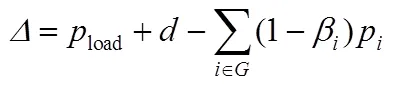
由表4可知，解析序列1表示的是网损不变的经济调度解析结果，其中的潮流校验后的不平衡量(网损)全部由平衡机组承担，对应的发电成本为6933.54$，以此为初始值，经7次序列解析，所得的考虑网损变动的经济调度最优发电成本为6838.91$，相对前者节省94.63$，说明本文方法由于考虑了协调方程引导下的机组功率最优分配与潮流方程引导下的网损产生物理规律的衔接与协调问题，可以取得更好的经济效益。其次，在序列解析过程中，式(18)始终满足，当机组输出功率趋于最优解时，不等式逐渐趋于等式，发电成本亦单调递减且趋于最小值，从而说明本文方法的正确性。

上述计算解序列，如果不进行对步长制约(取1时)，其变化如图2所示，可见该解序列是振荡且不收敛，这也表明文献[19]所给条件的苛刻性。由此，必须对凸特性和单调性予以通过步长的控制。对于如何选择最优步长，对本文研究内容而言，与发电机组成本特性有重要关系，不过本文每次基本是代数运算，故步长对计算速度的影响不是很显著的。

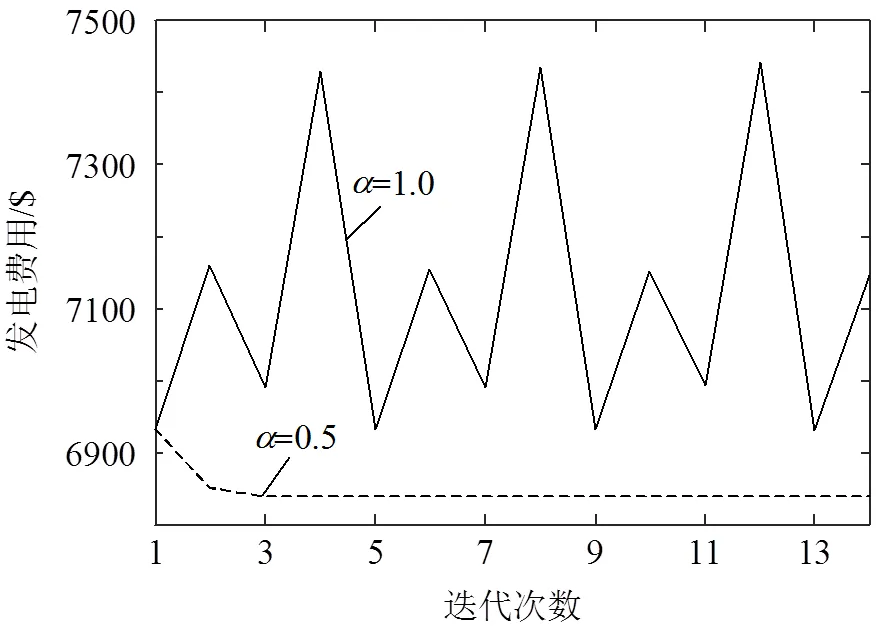
图2 解序列的震荡现象

7 结论

网损随机组功率变动的经济调度是一个复杂的优化问题，本文将传统和现代技术相结合，给出序列代数的快速求解方法，得到如下结论：

1）只要机组成本特性满足凸条件，计及网损变动的经济调度依然存在唯一最优解。

2）在一定条件下，网损随机组功率变动构成线性且满足凸特性的支撑超平面，研究这一支撑超平面的有效性对推进经济调度复杂性简化有重要意义。

3）当机组费用特性差异显著时，网损随机组功率变动的经济调度，会使机组输出功率发生显著性变化，充分显现市场机制下，研究这一问题的重要性。

4）按上述思路，电压随机组功率变动、电网制约随机组功率变动，可能也存在相应的规律，这对经济调度、优化潮流、机组组合等问题的简化处理有良好的前景。

[1] 薛晓岑，周保中，孙友源．能源互联网与发电企业[J]．发电与空调，2015，36(6)：35-37．

[2] 张舒，胡泽春，宋永华，等．基于网损因子迭代的安全约束机组组合算法[J]．中国电机工程学报，2012，32(7)：76-82．

[3] 王楠，张粒子，黄巍，等．电力系统安全经济调度网损协调优化方法[J]．电网技术，2010，34(10)：105-108．

[4] 张克，张尧，宋文南，等．市场条件下考虑网损的电厂有功功率分配[J]．电力自动化设备，2000，20(5)：15-17．

[5] 李昀昊，王建学，王秀丽．基于混合聚类分析的电力系统网损评估方法[J]．电力系统自动化，2016，40(1)：60-65．

[6] 王峥，刘创华，刘怡然，等．基于数据融合与拓扑分析的多阶段月度网损计算[J]．电力自动化设备，2015，35(9)：61-67．

[7] 张宏伟，朱建华，陈宁，等．110 kV电缆和架空线路用户无功补偿配置的方法研究和分析[J]．发电与空调，2016，37(2)：36-39．

[8] Happ B H．Optimal power dispatch-a comprehensive survey[J]．IEEE Transactions on Power Apparatus and Systems，1977，96(3)：841-854．

[9] Wood A J，Wollenberg B F．Power Generation Operation and Control[M]．Beijing：Tsinghua Universtiy Press，2003．

[10] Chowdhury B H，Rahman S．A review of recent advances in economic dispatch[J]．IEEE Transactions on Power Systems，1990，5(4)：1248-1257．

[11] 李彩华，郭志忠．电力系统优化调度概述(I)－经济调度与最优潮流[J]．电力系统及其自动化学报，2002，14(2)：60-63．

[12] Madrigal M，Quintana V H．An analytical solution to the economic dispatch[J]．IEEE Power Engineering Review，2000，20(9)：52-55．

[13] 孔祥玉，房大中，候佑华．基于直流潮流的网损微增率算法[J]．电网技术，2007，31(15)：39-43．

[14] 王正风，汤伟，吴昊，等．论等耗量微增率和等网损微增率与最优潮流的关系[J]．电力自动化设备，2007，27(4)：39-41．

[15] 陈恳，李小锐，徐敏，等．网损微增率新解法与转置雅克比矩阵法用于有功优化计算的比较[J]．中国电机工程学报，2000，20(7)：34-36，39．

[16] Hill E F，Steven W D．An improved method of determining incremental loss factor from power system admittances and voltages [J]．IEEE Transactions on Power Apparatus and Systems，1968，87(6)：1419-1425

[17] Sarkar V，Khaparde S A．DCOPF-based marginal loss pricing with enhanced power flow accuracy by using matrix loss distribution[J]．IEEE Transactions on Power Systems，2009，24(3)：1435-1445．

[18] 王主丁，刑颖华，冯祁山，等．网损微增率计算方法的研究(II)—有功经济调度三种计算方法的比较[J]．电力系统及其自动化学报，1995，7(1)：29-37．

[19] Torre D L，Galiana F D．On the convexity of the system loss function[J]．IEEE Transactions on Power Systems，2005，20(4)：2061-2069．

(责任编辑 杨阳)

A Fast Analytical Method for Economic Dispatch Considering Network Losses

LI Benxin1, HAN Xueshan1, JIANG Zhe2, LI Wenbo2

(1. Key Laboratory of Power System Intelligent Dispatch and Control of Ministry of Education (Shandong University), Jinan 250061, Shandong Province, China; 2. State Grid Shandong Electric Power Research Institute, Jinan 250003, Shandong Province, China)

When power network losses are assumed to be constant, an analytical solution was proposed to solve the economic dispatch problem given the unit consumption characteristics are convex. However, as the losses are actually varying with the outputs of the power generating units, the previous analytical method cannot be applied directly. Fortunately, based on the convexity of losses related to the unit’s power output as well as power flow equations, this paper proposes a fast-analytical method for economic dispatch with consideration of network losses. The proposed method converts the problem into several economic dispatch problems with constant losses and the optimal solution can be found in monotone finite algebraic calculus.

power systems; economic dispatch; power network losses; convexity

2017-10-20。

李本新(1987)，男，博士研究生，研究方向为电力系统稳定与控制，benxinli@163.com；韩学山(1959)，男，教授，博士生导师，主要研究方向为电力系统优化调度。

国家自然科学基金项目(51477091, 51177091)；国家电网公司科技项目(SGSDDK00KJJS1600061)。

Project Supported by National Natural Science Foundation of China (51477091, 51177091); Science and Technology Foundation of SGCC (SGSDDK00KJJS1600061).

10.12096/j.2096-4528.pgt.2018.015