灰狼算法在风电水电协同运行中的应用

李星，杨秀媛，王丽婕



灰狼算法在风电水电协同运行中的应用

李星，杨秀媛，王丽婕

（北京信息科技大学，北京市 海淀区 100192）

风电随机波动给电网的功率平衡带来了困难，因此出现了弃风问题。为了减少风电功率波动对电力系统功率平衡的影响，可以实行风电水电协同运行。充分利用水电的调节能力和风电的能量，用水电厂来平抑风电场输出功率的波动，通过控制水电机组实现风电水电协同运行，使风水协同系统按照计划输出功率。为了实现风电水电协同运行和提高风水协同输出的平稳性，采用灰狼算法优化水轮机PID控制，使水电可以稳定地跟踪风电的变化，使风电与水电出力按照计划输出。仿真结果验证了控制方法的有效性。

风电；水电；风水协同；灰狼算法

0 引言

风电的随机波动影响了电网的运行[1-3]。由于风的间歇性及随机波动大，因此需要调节电源应对风电功率的随机变化[4-5]。水电厂与风电场协同运行是解决风电波动问题的有效方法[6]。

为了提高水电机组的调节速度[7-9]，在电力系统允许风电水电协同运行的情况下，研究提高水电机组控制能力的方法，使其能够更好地协同风电运行。传统的PID控制器是水电站的水轮机控制系统广泛采用的控制器，无法满足风水协同运行要 求[10-12]。因此，该文采用灰狼算法优化PID参数的方案，改善水轮机的控制能力。

1 灰狼优化算法

灰狼优化(grey wolf optimizer，GWO)算法是Seyedali Mirjalili等人在2014年提出的一种新算法。该算法是根据灰狼的种群机制以及捕食行为推演出的寻优算法，能够通过不断迭代得到最优解。由于灰狼优化算法寻优精度高、收敛速度较快、鲁棒性强，能在迭代过程中不断调整收敛因子，实现种群的局部寻优和全局寻优，因此在实践中得到了广泛的应用[13-15]。灰狼算法已经应用到电力系统相关的优化问题中，如光伏发电、经济调度、水电站负荷优化分配等，均取得了较好的效果[16-19]。

灰狼优化算法基本原理如下。

1）分配种群内等级。

灰狼优化算法仿照灰狼群内的等级制度，一个狼群内可以划分为如图1所示的4种等级，分别为、、、。在搜索寻优过程中，由个体负责寻找路径，这3种个体优化和更新最佳的搜索路径，然后根据等级分配得到的一般解、次优解、最优解，得到一般解，得到次优解，则得到最优解。

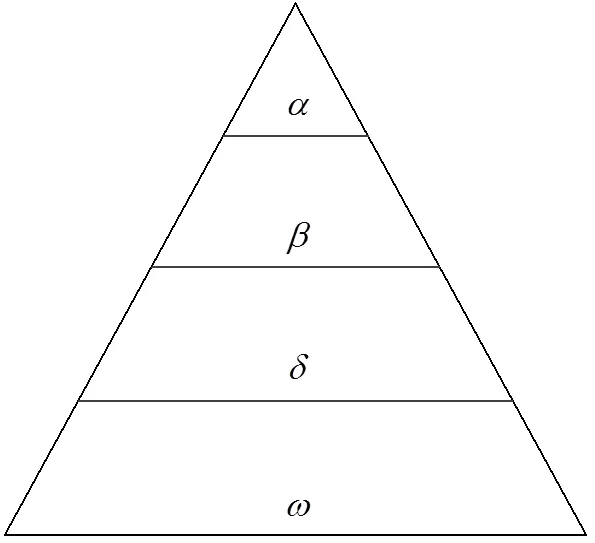
图1 灰狼群内等级示意图

2）寻找目标。

在灰狼的寻优过程中会通过各个方向去寻找目标的最佳路线。为了改善全局搜索性能，灰狼需要遍历整个路径。

3）进攻目标。

在攻击阶段，发出信息，使搜索个体进行移动，并可选择靠近目标还是远离目标。

灰狼优化算法的寻优步骤如下，算法流程如图2所示。

1）初始化。

首先对参数进行初始赋值，赋予循环次数、因子、步长系数和等的值。并在空间生成一个灰狼种群X(=1,2,¼,)。

2）在进行初始化后，根据公式算出每一个个体的函数值，然后按照从小到大的规律排列，如果优化的目标是最小值，则得到的函数值越小越好，最小值为最优的解。

3）接下来分配最优解、次优解、一般解，将函数值分别赋给、X和X。

4）根据式(1)—(3)得出其他的搜索个体与X、X、X和之间的距离，搜索个体改变的方向可以根据式(4)和(5)调整，由式(6)来更新搜索个体的位置。

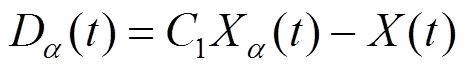
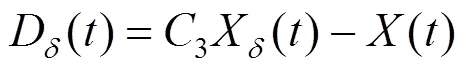
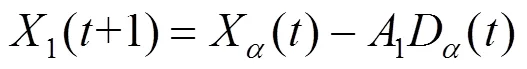
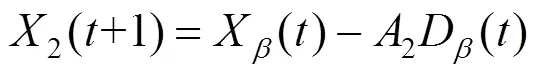
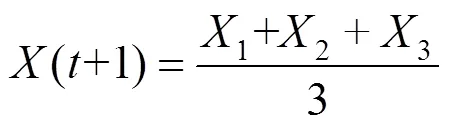
5）步长系数和按照式(7)、式(8)改变，其中12为变化因子，都是随机数。

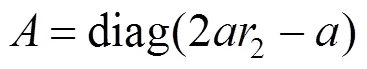
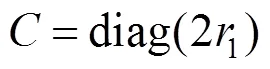
6）由上面的式子算出当前被更新的全部搜索个体的函数值。

7）更新完毕后，以最佳的目标函数值作为新的、X和X。

8）按照+1迭代，若溢出，那么跳转到步骤4），若，终止条件满足，则输出最优解，算法结束。

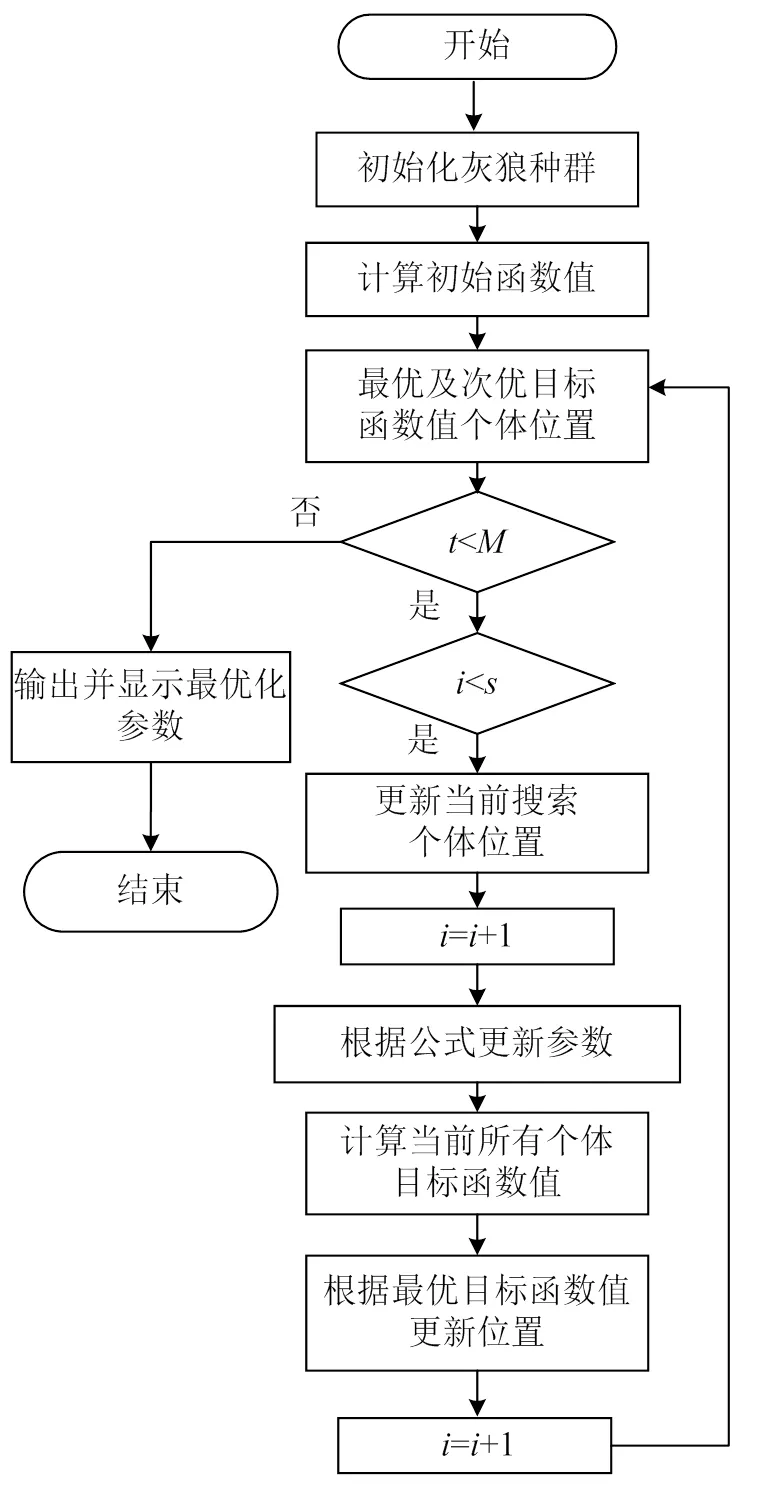
图2 灰狼优化算法流程图

由于灰狼算法特殊的计算原理，扩大了全局搜索能力，并且收敛速度快，稳定性好，复杂程度低，经过灰狼算法优化的水轮机调速器的鲁棒性大大加强。作为智能算法中效果比较好的新型算法，灰狼算法具有非常重要的研究意义[20-21]。

2 灰狼优化算法在风水协同发电控制中的应用

风水协同运行的原理：在风水协同运行过程中，理想的输出功率减去风电并网的输出功率，即为水轮机需要跟踪输出的功率，利用水电机组的调速装置控制水轮机的输出功率以求达到输出功率快速变化的目标。主要研究如何提高水电机组的响应速度。针对水轮机被控对象参数的不确定性提出用灰狼算法优化水轮机的PID控制器。灰狼算法优化的风水协同发电控制系统原理如图3所示。

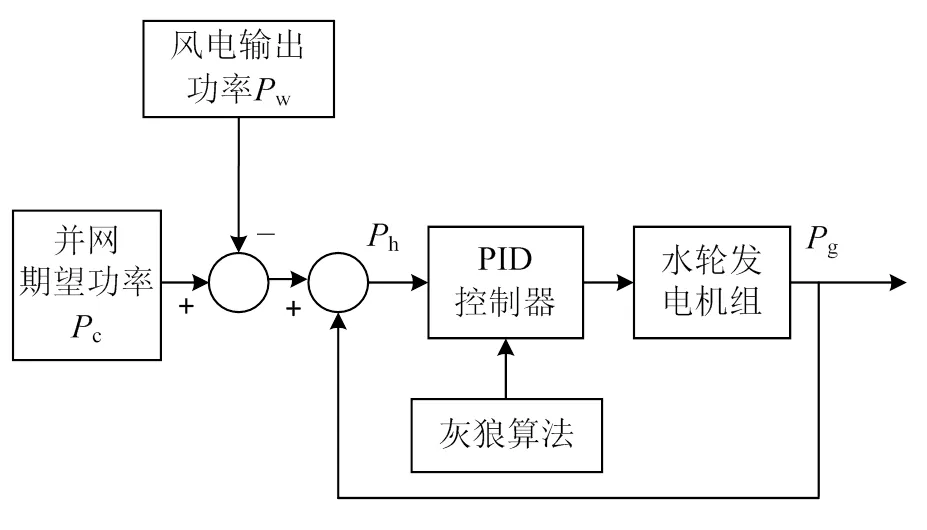
图3 风水协同运行原理图

图3中：c为并网期望功率；w为风电场输出功率；h为水轮机实际输出功率。c-w得到理想的水轮机发出的功率，把目标功率当做闭环控制的输入目标，通过调整调速器控制水流的输出，进而通过水轮发电机组输出相应大小的功率以满足风功率不足导致的缺额功率。

PID调速器为水轮机控制系统固有的控制器，其动态特性为：

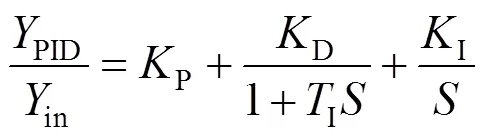
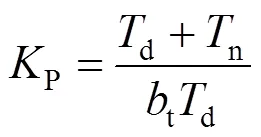
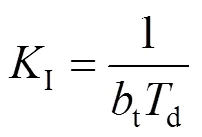
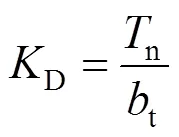
式中：PID、in分别为PID控制器的输出和输入变量；P为比例增益，整定范围为0.5~20s；I为积分增益，整定范围为0.05~10s；D为微分增益，整定范围为0~5s；t为暂态转差系数，整定范围为0~1s；d为缓冲时间常数，整定范围为2~20s；n为加速度时间常数。

工程中只计算水轮机机械液压系统线性部分，其传递函数为

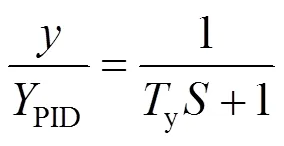
式中：为接力器行程；y为接力器响应时间常数，整定范围为0.05~0.25s。

水轮发电机及负荷的传递函数为

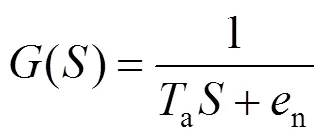
式中：a机组惯性时间常数；n为发电机负载的自调节系数。

3 算例仿真分析

仿真算例是根据二滩电站水轮机组模型参数及采用双馈型风电机组装机容量为1000MW的风电场模型搭建而成。

3.1 阶跃仿真

系统在阶跃函数作用下的工作条件是比较严峻的，也具有代表性，因此，首先采用阶跃信号作为水轮机的输入，给定功率标么值为1，见图4和图5。运用MATLAB的M语言编写、运行灰狼算法优化PID调速器程序。灰狼种群的规模为100，迭代的次数为200。经过200次的迭代，结果逐渐逼近理想值，经过灰狼算法计算，得到优化后的PID参数，P=3.605，I=0.102，D=0.238，设仿真时间为350 s，得到水轮机输出功率曲线和误差曲线如图6所示。

图4 风电机组输出功率

图5 水轮机组输入功率

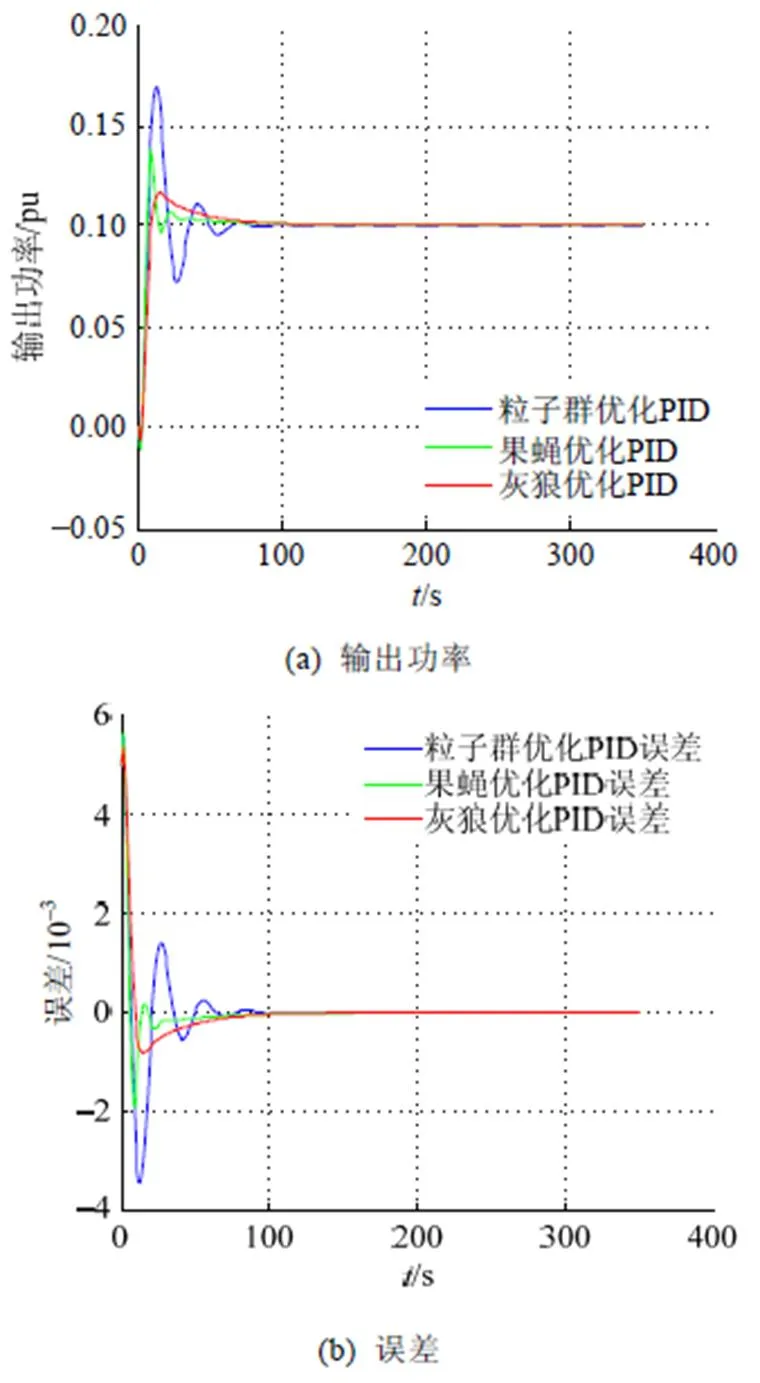
图6 水轮发电机组的阶跃响应曲线

图6表示经过灰狼算法优化PID参数的水轮机输出功率与其他2种算法优化的水轮机输出功率的对比。因为自动控制原理中的动态性能指标能够反映系统的性能，从上升时间、调节时间、超调量等计算系统的性能，得到3种算法的动态性能指标比较，见表1。

通过比较可以看出，经过灰狼算法优化的系统相比其他优化算法具有超调量小、响应速度快的优点。

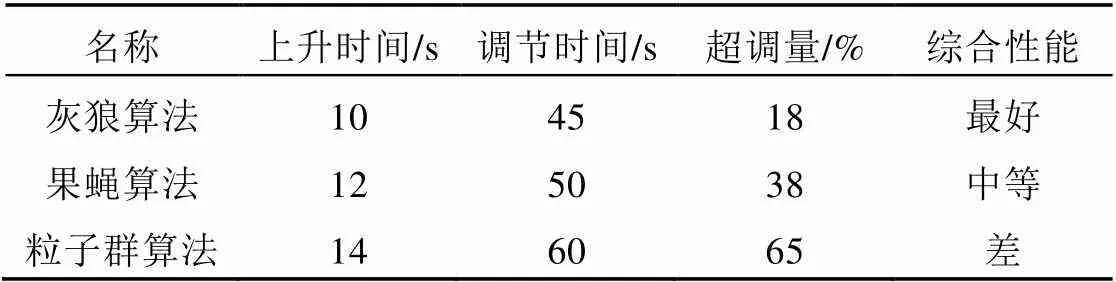
表1 3种算法的动态性能指标比较

之后，在运行过程中突然加一个上阶跃信号和下阶跃信号，以此来测试系统的响应能力，得到水轮机组输出功率曲线如图7所示。可见，灰狼算法的确具有优势。

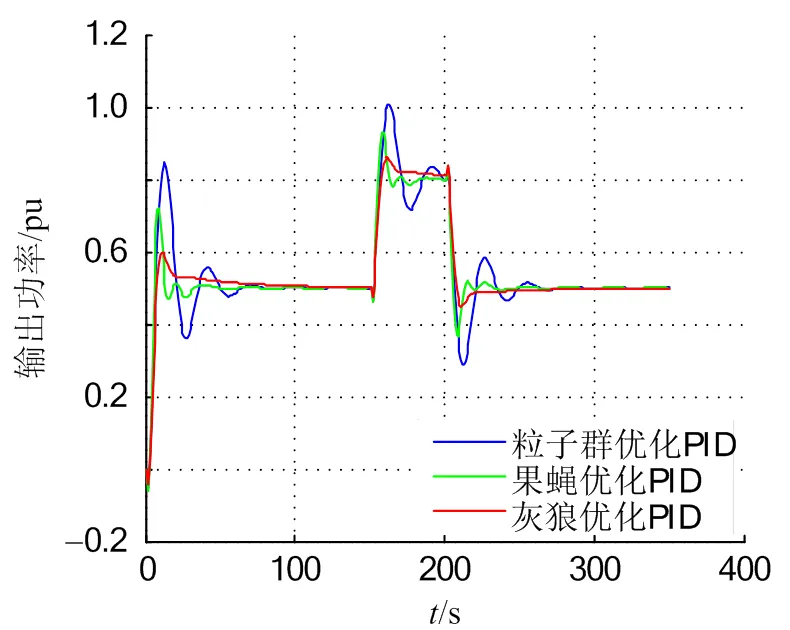
图7 水轮发电机组的响应曲线

3.2 实际数据仿真

采用某风电场的实时数据，分别选取了春夏秋冬4个季节的典型风力数据，每15 min采集一次，一天内共采集96个点，运行MATLAB环境下灰狼算法优化水轮机调速器的程序，得出不同季节风水协同总输出功率曲线，如图8—11所示。可见，利用灰狼算法，水电机组可以有效地补偿风电的功率波动，使得风电水电协同运行的总输出功率基本保持平稳，有利于发挥风电等新能源的作用，对于充分利用新能源具有重要意义。

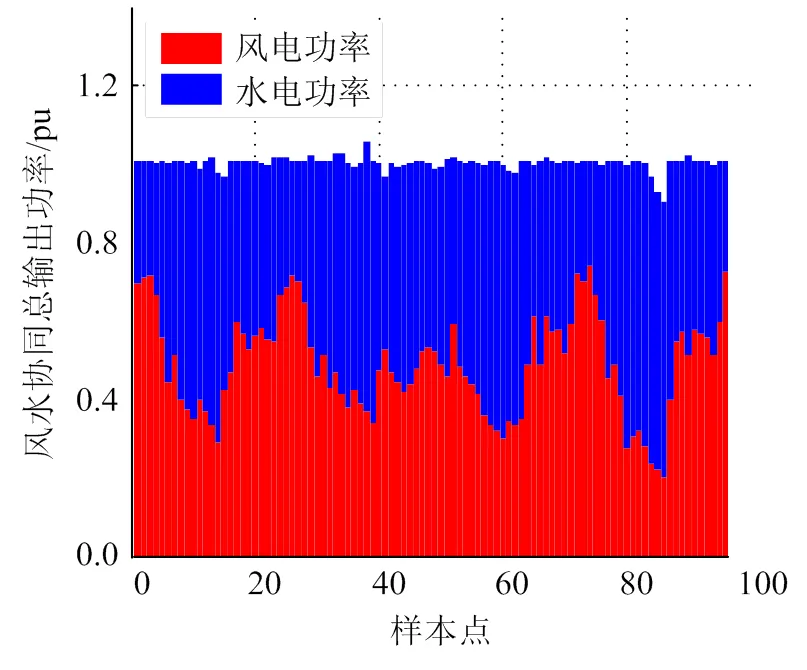
图8 春季风水协同总输出功率

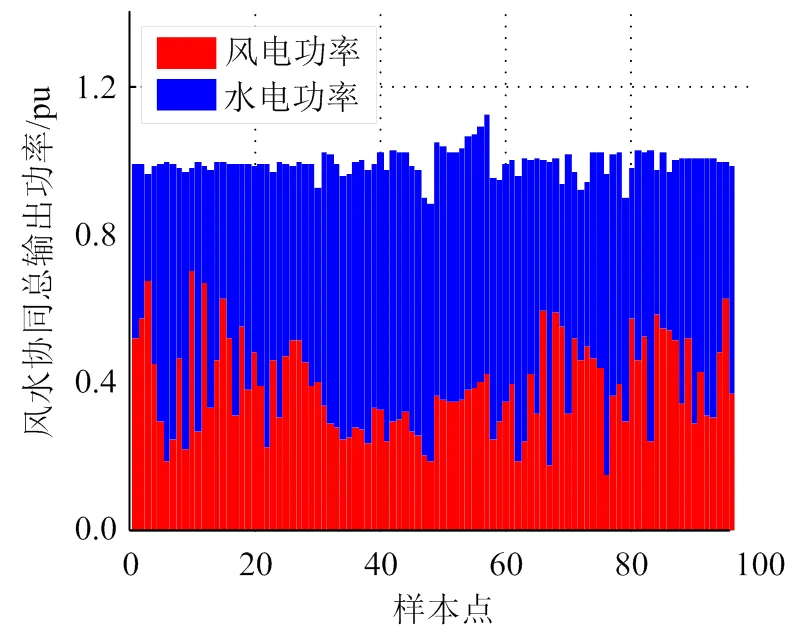
图9 夏季风水协同总输出功率

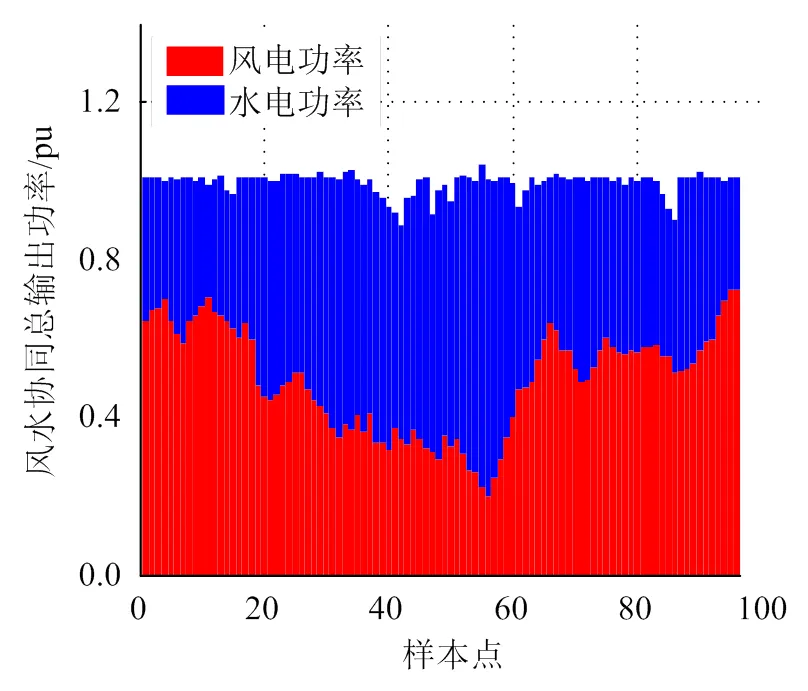
图10 秋季风水协同总输出功率

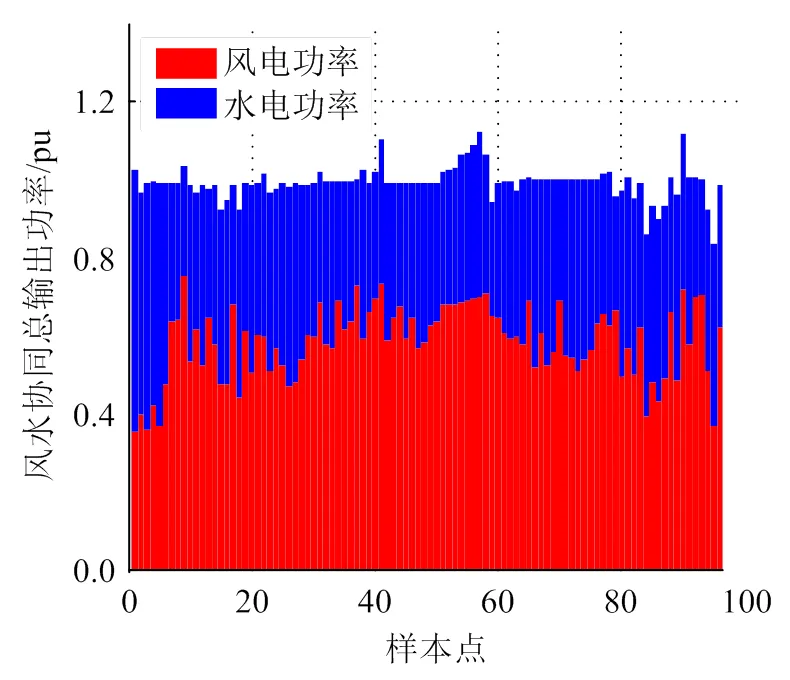
图11 冬季风水协同总输出功率

4 结论

研究了灰狼优化算法在风电水电协同运行中的应用。以风电水电协同发电的水电厂调速器的PID参数为优化对象，通过算法得到控制参数的最优值。利用灰狼算法，水电机组可以有效地补偿风电的功率波动，使得风电水电协同运行的总输出功率基本保持平稳，有利于发挥风电等新能源的作用，对于充分利用新能源具有重要意义。

采用灰狼算法优化的系统相比果蝇优化和粒子群优化算法具有超调量小、响应快速以及调节快速的优点，能够更好地发挥风电水电协同系统的作用，在风水协同控制系统中具有很好的应用前景。

[1] 王凤蛟，李鹏．电力体制改革背景下发电集团面临的挑战和机遇[J]．发电与空调，2017，38(3)：51-55．

[2] 杨秀媛，陈瑶，陈麒宇，等．导前微分控制在风电水电协同运行中的应用[J]．中国电机工程学报，2015，35(18)：4591-4597．

[3] 王学成，杨雨．基于发电效益最大化的水光互补方案优化设计[J]．发电与空调，2015，36(6)：27-30，56．

[4] 兰维，张中泉，雷阳．风电机组出力性能分析方法研[J]．发电与空调，2017，38(3)：26-29．

[5] 范永威，潘文霞．风-水电联合优化运行分析[J]．太阳能学报，2008，29(1)：80-84．

[6] 周宇昊，张海珍，宋胜男．多能互补分布式能源实验平台系统关键技术研究[J]．发电与空调，2017，38(6)：5-9，37．

[7] 孙春顺，王耀南，李欣然．水电-风电系统联合运行研究[J]．太阳能学报，2009，30(2)：232-236．

[8] 尚志娟，周晖，王天华．带有储能装置的风电与水电互补系统的研究[J]．电力系统保护与控制，2012，40(2)：99-105．

[9] Chen Q，Littler T，Han S．Large-scale wind generator cascaded tripping[C]．Proceedings of the 3rd IEEE Conference on Computer Science and Automation Engineering，Guangzhou，China，2013．

[10] Chen Q，Littler T，Wang H．Tripping control for transient stability in coordinated hydro and wind generation

[J]．Proceedings of IET International Conference on Renewable Power Generation Conference 2013(RPG 2013)，Beijing，China，2013：1-4．

[11] 韩方冰．基于风电水电联合运行的中长期机组组合研究[J]．大连理工大学学报，2013，25(10)：103-106．

[12] 吴虎胜，张凤鸣，吴庐山．一种新的群体智能算法一狼群算法[J]．系统工程与电子技术，2013，35(11)：2430-2438．

[13] 静铁岩，吕泉，郭琳．水电-风电系统日间联合调峰运行策略[J]．电力系统自动化，2011，35(22)：97-103．

[14] 罗佳，唐斌．新型灰狼优化算法在函数优化中的应用[J]．兰州理工大学学报，2016，42(3)：96-101．

[15] 苏永亮，周彬．基于自适应粒子群算法的水轮机PID调速参数优化[J]．水电厂自动化，2014，35(2)：47-50．

[16] 方红庆，沈祖诒．基于改进粒子群算法的水轮发电机组PID调速器参数优化[J]．中国电机工程学报，2005，25(22)：123-127．

[17] Lansberry J E．Optimal hydrogenerator governor tuning with a genetic algorithm[J]．IEEE Transactions on Energy Conversion，1992，7(4)：623-630．

[18] 周强，周永全．一种基于领导者策略的狼群搜索算法[J]．计算机应用研究，2013，30(9)：2629-2632．

[19] 张新明，涂强，康强，等．强化狼群等级制度的灰狼优化算法[J]．数据采集与处理，2017，32(5)：879-889．

[20] 陈涵．基于灰狼算法的水轮机调速器参数优化[D]．武汉：华中科技大学，2016．

[21] 施行之，周宇昊．分布式能源系统的多目标优化模型研究[J]．发电与空调，2015，36(2)：1-4．

(责任编辑 车德竞)

Grey Wolf Algorithm in Coordinated Hydro and Wind Power Generation

LI Xing, YANG Xiuyuan, WANG Lijie

(Beijing Information Science & Technology University, Haidian District, Beijing 100192, China)

Wind is stochastic that trouble the grid power balance and make wind curtailment occur. The wind power and hydropower could cooperate operation to reduce the influence of wind power fluctuation. Through making full use of the regulating ability of hydropower and wind energy, the coordinated operation of wind power and hydropower can be realized by controlling hydropower units, so that the wind and hydropower coordinating operation system will output according to the plan, stabilize the power system. To achieve the coordinated operation of wind power and hydropower and improve the stationarity of the coordinate output, the Grey Wolf algorithm was used to optimize the PID control of hydraulic turbine, to facilitate hydropower steadily track the change of wind power and make the output of wind power and hydropower output according to plan. The simulation results verified the effectiveness of the method.

wind power; hydropower; wind and hydropower coordinating operation; grey wolf optimizer algorithm

2017-12-16。

李星(1991)，男，硕士研究生，研究方向为风水协同运行控制，1534703887@qq.com；杨秀媛(1962)，女，副教授，主要从事 含新能源的电力系统分析与规划方面的研究工作；王丽婕(1980)，女，博士，副教授，研究方向为电气自动化控制。

国家自然科学基金项目(51377011，51607009)。

Project Supported by National Natural Science Foundation of China (51377011, 51607009).

10.12096/j.2096-4528.pgt.2018.007