基于弹性基础柔性梁的重载轮胎面内胎体与胎侧耦合建模及参数辨识
刘志浩, 高钦和, 刘 准, 王 旭
(火箭军工程大学 兵器科学与技术军队重点实验室, 西安 710025)
重载轮胎作为军用车辆与地面直接接触的部件,其力学特性直接影响车辆动力学特性。整车的主要性能指标的研究,如平顺性[1]、动力性、纵向[2]、侧向稳定性[3]等都和轮胎模型密不可分。
重载轮胎与乘用车轮胎和卡车轮胎相比,具有重型化承载的特点,广泛应用于武器发射平台,其平均轴荷在10~13 t,且为了保证其越野特性,重载轮胎具有较大的扁平率,如图1所示。
轮胎面内特性[4]直接影响轮胎的垂直振动、包容特性和滚动阻力等,直接影响汽车的平顺性、声噪、动力性和燃油经济性。由于轮胎具有极其复杂的结构,具有材料非线性和几何非线性,因此基于面内特性分析轮胎测试与建模属于汽车动力学研究的难点之一。而模态测试则是一种求取结构模态频率和阻尼、进行结构动态特性分析的重要方法,广泛应用到车辆动力学建模与测试中。

图1 不同轮胎的扁平比Fig.1 Flatness ratio of different kinds of tires
现有的研究方向大多集中在轿车或乘用车的动态特性分析,主要有:Fan等[5]及其课题组,利用模态测试的方法获取了胎体与轮毂间的耦合振动模态;葛剑敏等[6]利用试验模态的方法分析了气压和轮胎质量对轮胎固有频率的影响,高海慧等[7]通过试验模态的方法研究充气压力对模态参数的影响规律,而对重载子午胎开展模态试验研究文献的却很少。
重载轮胎气压高,阻尼低,花纹粗大,且较大的扁平比的结构特点致使在滚动过程中的噪声主要来源是结构振动,且随着重载车辆速度提高至70 km/h[8],结构振动噪声占轮胎噪声的比重达到65%,如图2。

图2 轮胎噪声贡献率图Fig.2 Contribution factors of tire rolling noise
胎体与路面直接接触,路面不平度经胎体和胎侧、空腔传至轮辋,如图3(a)所示,轮辋的传递响应由结构振动响应和结构-空腔耦合振动构成,其中胎体-胎侧-轮辋传递路径属于结构振动,胎体-空腔-轮辋传递路径属于结构-空腔耦合振动[9],图3(b)列举了重载轮胎胎体锤击实验时,胎体及轮辋的响应传递函数(0~300 Hz),其中结构振动集中在59 Hz和170 Hz附近,而结构-空腔耦合振动为120 Hz(一阶)和240 Hz(二阶),与普通轿车、乘用车轮胎的一阶结构-空腔共振频率(230~250 Hz)[10]不同,但结构-空腔耦合振动幅值较小(见图3(b)),可忽略。因此开展基于轮胎结构模型的轮胎体内特性分析方法具有重要意义,而弹性基础的环模型为轮胎振动解析模型的代表,可划分为刚性环模型和柔性环模型。
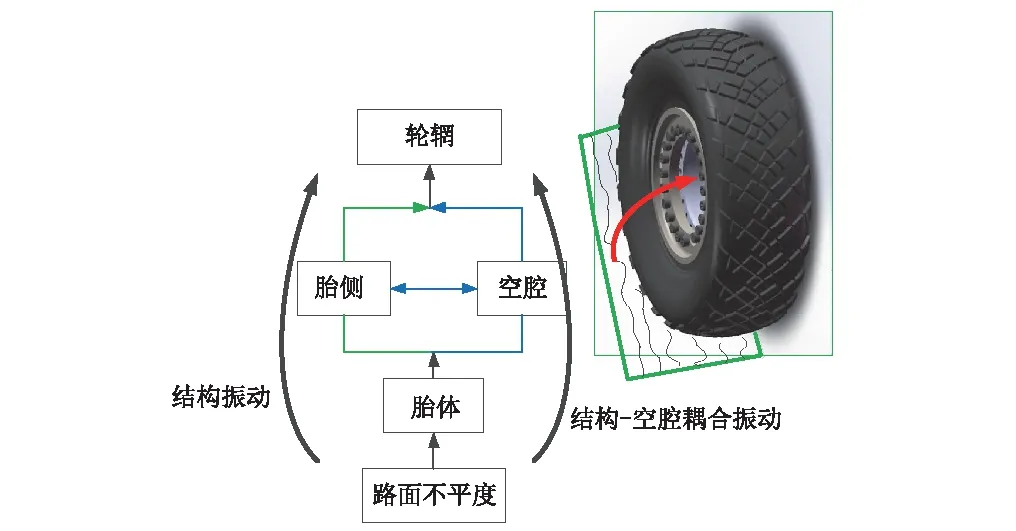
(a)路面激励作用下的轮胎振动传递
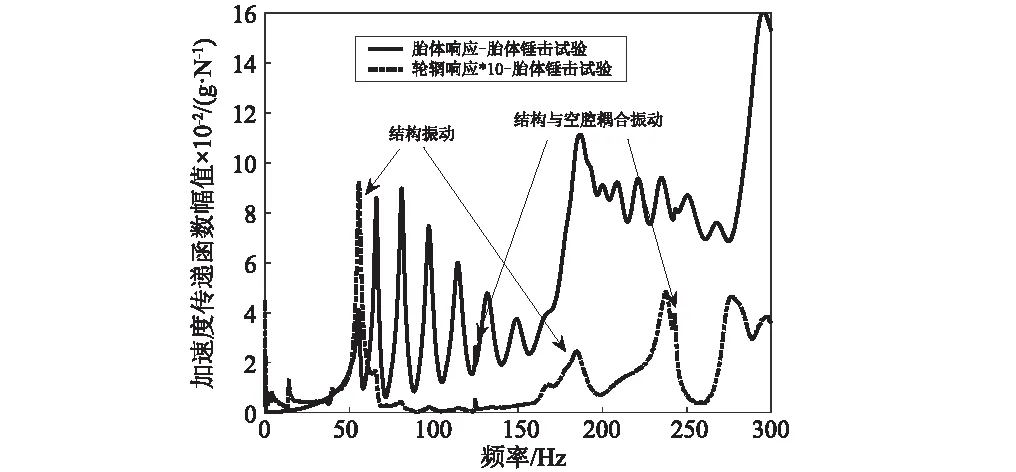
(b)面内锤击实验图3 重载轮胎体内振动特性Fig.3 In-plane vibration characteristic of heavy loaded radial tire
刚性环模型[11]假定胎体为刚性环,并引入一个表征残余刚度的弹性单元,与之相对应的是柔性环模型[12-13],将轮胎简化成弹性基础上的圆环,弹性环代表胎冠,沿圆周分布的径向和切向弹簧表示胎侧和充气效应,轮辋由集中质量表示,柔性环模型可实现胎体的变形与振动。相比较,刚性环模型只可表征胎体与轮辋的错动阵型,因此其分析频段为70~80 Hz以下(一阶错动频率),只考虑错动阵型,而忽略高阶模态以及高阶模态所对应的胎体振动,无法实现对高阶模态的预测;柔性环模型属于物理解析模型,具有较宽频带的动力学仿真能力,且柔性环模型所用参数可以反应轮胎自身的特性而与工况无关,并可充分考虑轮胎的材料和几何非线性,提高了轮胎建模的科学基础,同时也可省略刚性环模型中对路面的预处理,并且轮胎的振动特性均能求取解析解或者得到数值解,以上的文献对比中,均集中于分析柔性胎体与轮辋质量块的耦合振动,图3(b)中轮辋的结构振动响应存在两个峰值,59 Hz和170 Hz附近,59 Hz为柔性胎体与轮辋的相对错动,该特征已被准确表征,而170 Hz附近的振动则基于柔性胎体和轮辋质量块的建模方法无法表征,因此开展基于胎侧单元周向分布的柔性环模型建模及实验研究,分析重载轮胎及其他扁平比较大轮胎的面内振动特性,包括:①提出考虑柔性胎体-周向分布胎侧单元-轮毂质量块耦合作用面内振动模态测试与分析方法;②提出基于柔性梁的面内柔性胎体-周向分布胎侧单元-轮毂质量块耦合作用建模与求解方法。
本文的研究思路如图4所示,采用移动力锤激励的方法,测试胎体、胎侧和轮毂处的振动响应,分析重载轮胎胎体-胎侧-轮毂的耦合试验模态;利用欧拉梁对胎体的面内弯曲变形进行建模,并将胎侧等效为离散质量块的惯性力和分段弹簧,建立胎体-胎侧-轮毂的耦合动力学方程;利用测试的模态参数对方程中的结构变量进行辨识,并验证。

图4 建模流程图Fig.4 Scheme of research
1 重载轮胎胎体-胎侧-轮毂耦合模态试验研究
搭建重载轮胎胎体-胎侧-轮毂的耦合模态测试系统,获得轮胎标准充气压力下的耦合模态参数,包括:固有频率、阻尼和模态阵型。
1.1 重载轮胎简介
GL073A ADAVANCE轮胎为重载子午胎,其胎侧径向长度与胎体宽度比值为0.98,结构参数如下表所示。规格为:16.00R20 173G,18层级,最高时速为G(90 km/h),充气断面宽为438 mm,充气外直径1 320 mm,额定充气压力为800 kPa,最大负荷为6 500 kg。
1.2 试验模态测试系统
搭建重载轮胎胎体-胎侧-轮毂耦合模态测试系统,如图5所示,包括:自由状态支撑装置、力锤及电荷放大器、数据测试系统和PC计算机,将PCB振动传感器分别粘贴于轮胎的胎体、胎侧和轮毂,采用遍激励的方法,沿胎体17个点进行径向激励,采用B&K力锤传感器和朗斯的电荷放大器,B&K力锤传感器将锤击力转化为电荷,后经电荷放大器,转化为DE-43数据采集器可识别的电压信号。
对标准充气压力下的胎体径向激励-胎体径向响应、胎体径向激励-胎侧径向响应和胎体径向激励-轮毂径向响应的传递函数,利用最小二乘复指数法[14]估计频率、阻尼和参与因子,求得的频率和阻尼如表1所示,阵型如图6所示,并求取各阶模态间的MAC值如图7所示。将实验传递函数、柔性胎体-周向分布胎侧单元耦合模态解析传递函数和只考虑柔性胎体模态的解析传递函数进行比较没如图8所示。
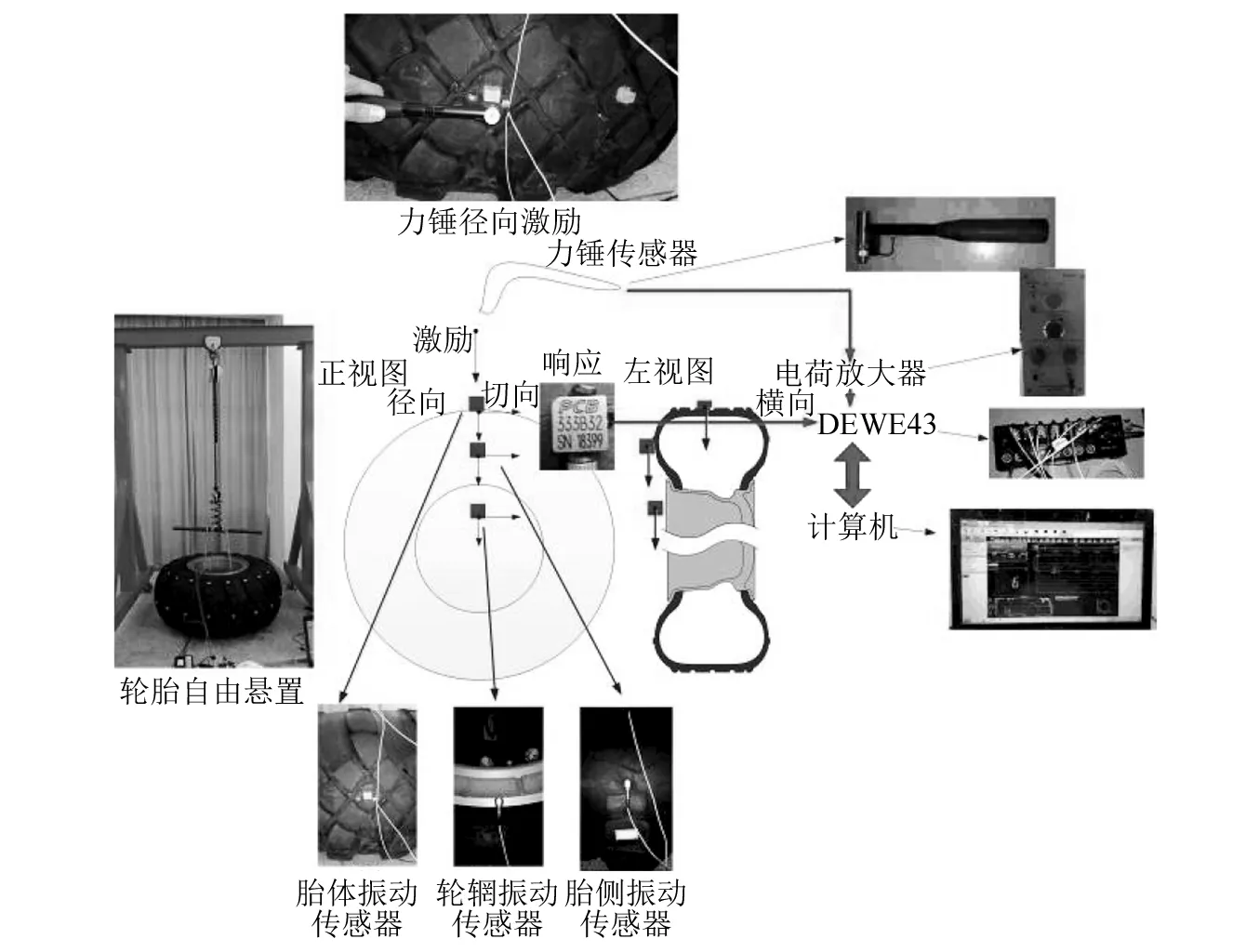
图5 重载轮胎模态测试系统Fig.5 Experimental modal system of heavy loaded radial tire
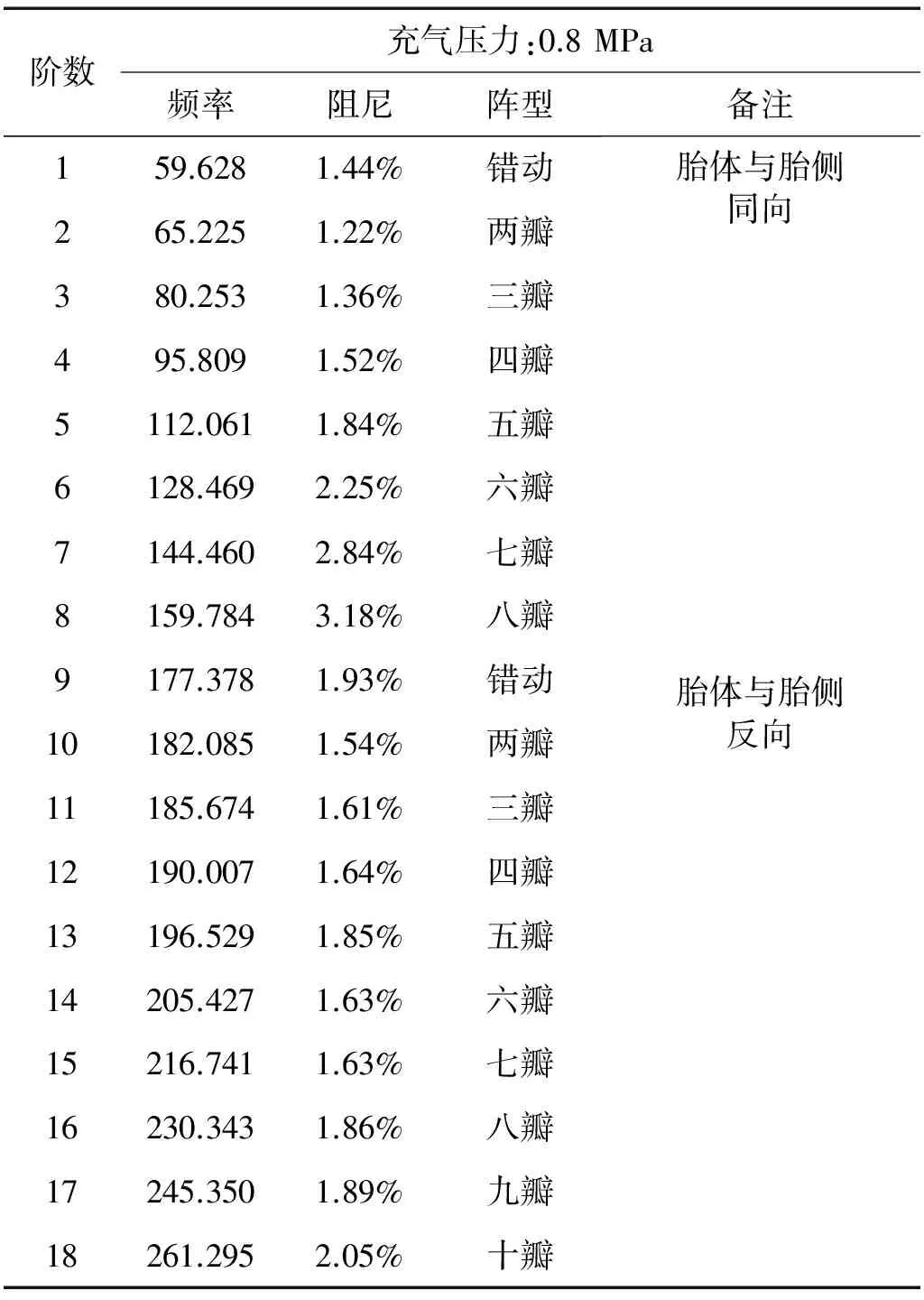
表1 胎体-胎侧-轮毂振动模态频率和阻尼

图6 重载轮胎模态阵型图Fig.6 Modal shape of heavy loaded radial tire
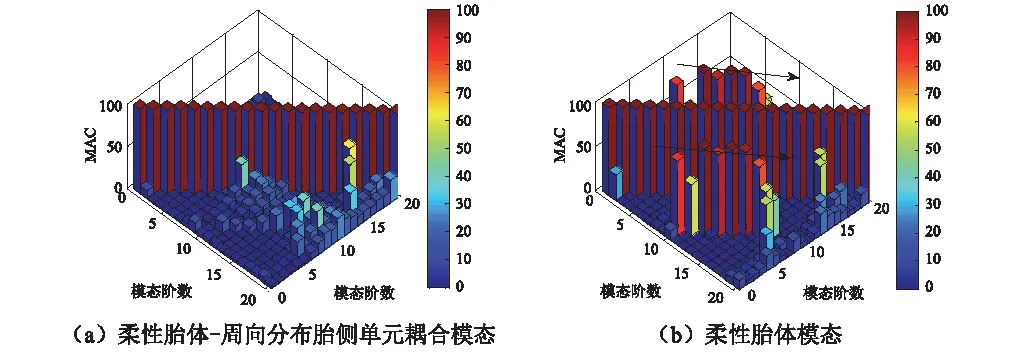
图7 MAC矩阵值Fig.7 MAC matrix
重载轮胎胎体-胎侧-轮辋耦合试验模态结果表明:
(1)如图7(b)所示,第1阶和第9阶,第2阶和第10阶,第3阶和第11阶,第4阶和第12阶,第5阶和第13阶,第6阶和第14阶,第7阶和第16阶,第8阶和第17阶均相互存在线性关系,MAC值为1,与模态向量正交相矛盾;
(2)忽略第9~17阶模态,则模态参数拟合的传递函数与试验传递函数误差达到59.25%,且无法表征重载轮胎180 Hz以上的振动特性,如图8所示;
(3)如图7(a)所示,胎体-胎侧-轮毂耦合的模态参数测试和分析方法求取的模态参数,MAC值除个别点外,MAC值均小于0.2,各阶模态间相互正交,证明了基于柔性胎体-周向分布胎侧单元-轮辋质量块耦合的模态参数测试分析方法的准确性;
(4)重载轮胎的阵型符合谐波特性,在0~180 Hz以内表现为胎体与胎侧的同向振动,在180~300 Hz内表现为胎体与胎侧的反向振动,如图6所示。
分析原因为:该特性由于其结构造成的,重载轮胎充气压力较大,承载较重,要求胎侧具有较厚的钢丝帘线层来防止重型承载的爆胎现象,胎侧与胎体的质量比增大,路面不平度作用于胎体时,在胎侧传递时,由于重载轮胎具有较大的扁平比,胎侧共振的波长较大,其发生共振的频率会降低,若只考虑柔性胎体的模态特征,则180~300 Hz内的柔性胎体和周向分布胎侧的反向振动则无法表征,因此在分析重载轮胎0~300 Hz频段内的面内振动时需将柔性胎体和周向分布胎侧的耦合效应考虑在内,该模态试验首次揭示了重载轮胎的柔性胎体与周向分布胎侧的耦合特征,为面内振动特性建模指明了方法。
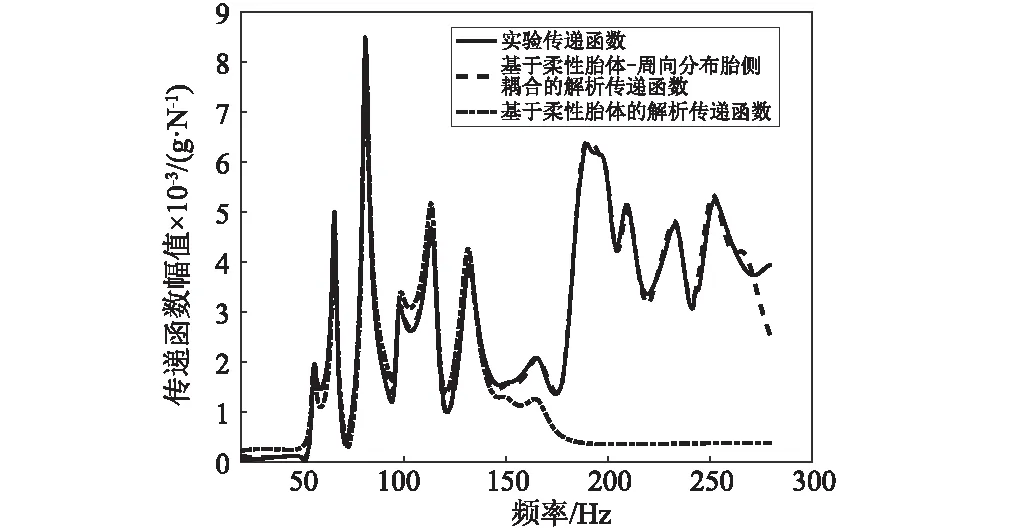
(a)传递函数幅值

(b)传递函数相位角图8 实验和解析传递函数比较Fig.8 Experimental and analytical transfer function
2 基于弹性基础柔性梁的面内胎体与胎侧耦合动力学建模及求解
2.1 面内胎体与胎侧耦合动力学建模
假设:胎体梁各截面的中心惯性轴在同一平面xoy内外载荷作用在该平面内,梁在该平面作横向振动(微振),梁的主要变形是弯曲变形[15],在低频振动时可以忽略剪切变形以及截面绕中性轴转动惯量的影响。
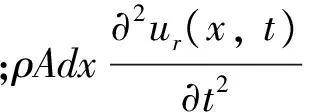

(a)连续胎体Euler梁
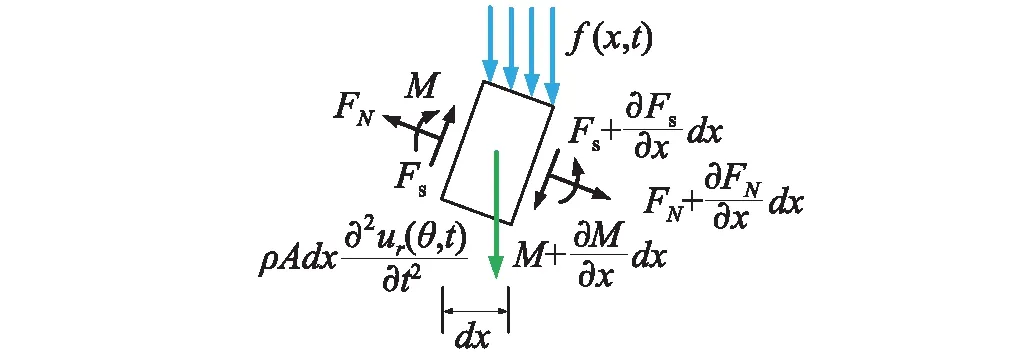
(b)欧拉梁微段图9 受力分析Fig.9 Force analysis
力平衡方程
(1)
以右截面上任一点为矩心,忽略轴向力对力矩平衡条件的影响
(2)
整理得
(3)
由材料力学知,弯矩和挠度的关系
(4)
则梁的动力学方程
(5)
式(5)中的预紧力FN如图10所示。
(6)
整理得
(7)
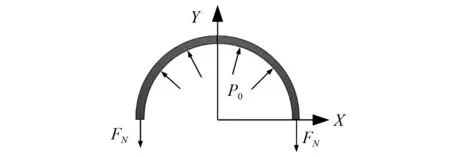
图10 充气压力造成的胎体轴向力Fig.10 Pre-tension of inflation pressure
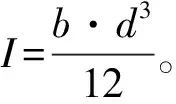
根据,x=Rθ,则胎体方程转化为
(8)
根据以上推导的胎体弯曲梁模型,考虑胎侧的惯性力,见图11。

图11 胎体-胎侧-轮毂耦合结构模型Fig.11 Coupled kinematic of carcass, sidewall and hub
建立胎体-胎侧-轮毂耦合动力学方程
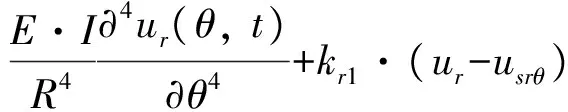
(9a)

(9b)
(9c)
式中:式(9a)为胎体弯曲梁振动方程;式(9b)为胎侧质量块振动方程;式(9c)为轮毂振动方程。
2.2 重载轮胎耦合动力学方程求解
胎体-胎侧-轮毂耦合动力学模型为偏微分方程组,利用模态叠加法[16],将偏微分方程组转化为空间和时间的常微分方程进行求解,推导出轮胎各阶固有频率与轮胎结构参数间的关系。
令

(10)
代入轮毂振动方程,推导出
(11)
结果表明:①轮毂在1阶模态与胎侧存在耦合关系;②当n≠1时,Rwn=0,高阶模态不会影响到轮毂的位移。
则轮毂的振动uwr(t)简化为
uwr(t)=Rw1sinωnt
(12)
当n=1时,方程组简化为
(13)
即
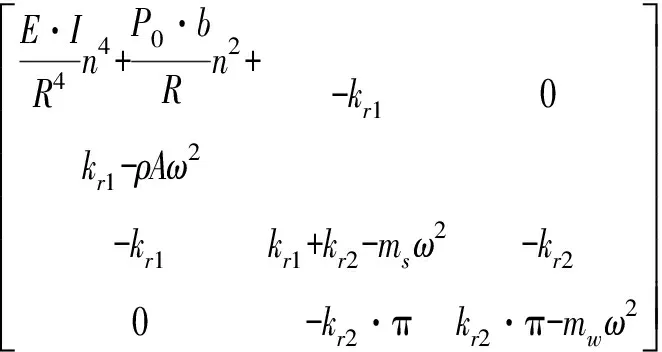
(14)
当n≠1,方程组简化为
(15)
即
(16)
为使上述n≠1时方程成立,则
(17)
化简为
(18)
解得
(19)
其中,
则
(20)
(21)
3 重载轮胎结构参数辨识及验证
3.1 结构参数辨识
重载轮胎的模态参数解析解中的参数包括几何参数和物理参数两部分,如表2所示。

表2 GL073A型重载轮胎几何与结构参数
利用轮胎标准气压下的模态参数,利用遗传算法[17]对轮胎动力学方程中的结构参数进行辨识。
其优化流程如图12所示。
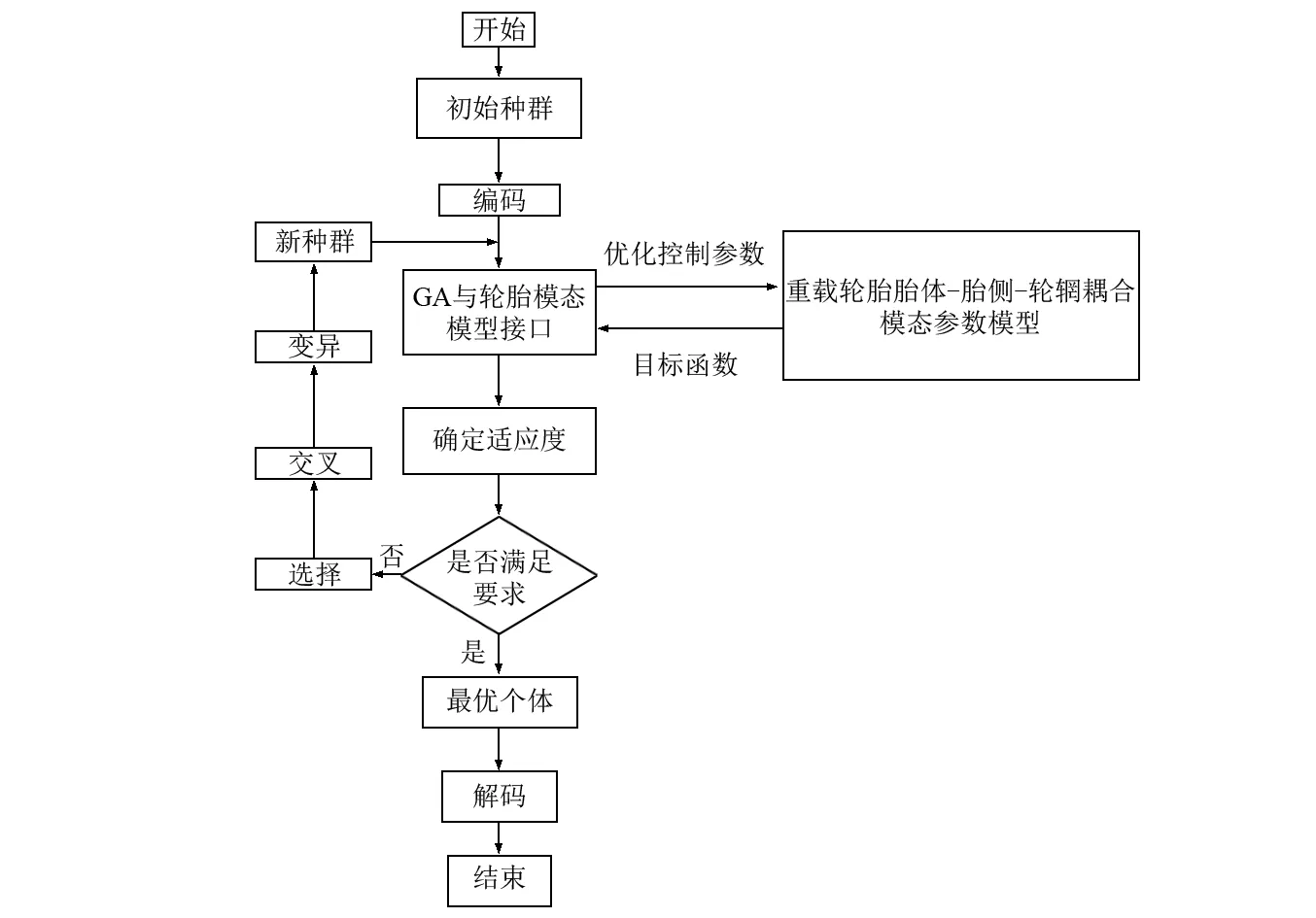
图12 遗传算法轮胎结构参数优化流程图Fig.12 Schemes of structural parameters identification
编码操作把需要解决的问题从解的空间转化到便于搜索的求解空间,而解码操作则与编码过程相反,由解的空间转换为问题空间。遗传算法的确立分为:基本参数的确定、变量范围的确立、选择算子和系数的确立、目标函数的确定,如表3所示。
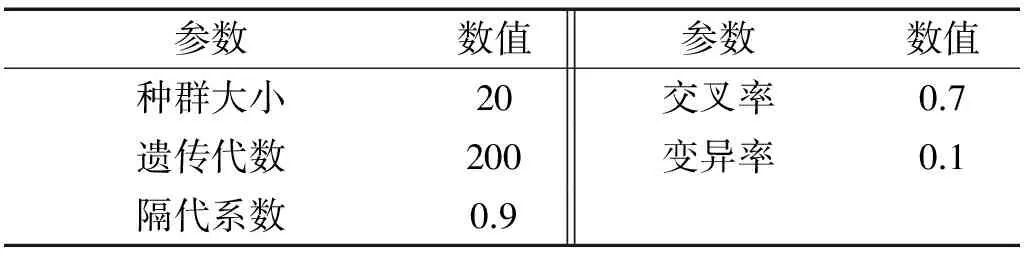
表3 遗传算法结构参数
其中,选择过程就是通过选择群体中生命力较强的个体来产生新的群体,而选择的过程,则是通过选择算子完成个体间优胜劣汰的操作的。本文采用轮盘赌选择算子,即个体可被选择的概率等于其适应度值在群体中各个个体适应度之和中占的比重,其中适应度值越高,被选中的概率就越大,进行遗传操作的可能性就越大。对选择的两个个体采用单点交叉的方法进行重组,从而产生两个新的个体。
(22)
选取重载轮胎胎体与胎侧3~6瓣阵型的同向和反向的模态频率,利用式(20)和式(21),以误差的均方值优化目标函数,如式(23)所示。
(23)
遗传算法优化过程如图13所示,结果如表4所示。
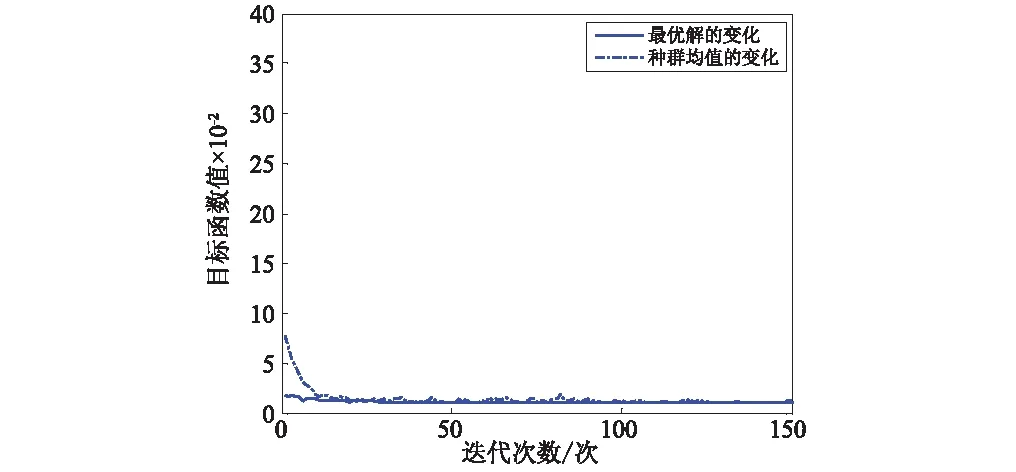
图13 遗传算法优化过程Fig.13 Optimization procedure

符号参数物理意义kr16.686×106kr24.431×106E·I25.697
3.2 模态预测
利用表4的轮胎辨识结构参数,对轮胎的固有频率进行对比分析,如图14所示。
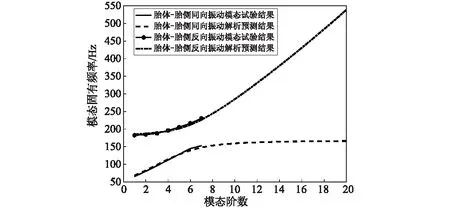
图14 模态试验结果与模型预测结果对比图Fig.14 Compared result of experimental and analytical modal resonant frequency
结果表明:①基于弹性基础的柔性梁模型理论模态预测值和实测值的误差在3%以内,说明了基于弹性基础的柔性梁模型对于分析重载轮胎在0~300 Hz内的胎体-胎侧-轮辋耦合模态的可靠性;②重载轮胎的胎体与胎侧的同向振动随着模态阶数的升高,收敛于175 Hz;③重载轮胎的胎体与胎侧的反向振动随着模态阶数的升高成指数增长;④重载轮胎的高频振动形式主要变现为胎体与胎侧的反向振动。
4 结 论
本文针对扁平比接近1的重载轮胎,提出一种面内振动模态测试与动力学建模方法,包括:①提出考虑柔性胎体-周向分布胎侧-轮毂质量块耦合作用面内振动模态测试与分析方法;②提出针对重载轮胎体内胎体-胎侧-轮辋耦合作用的弹性基础柔性梁动力学建模与参数辨识方法。通过理论建模、模态求解和试验模态分析。得到以下结论:
(1)重载轮胎的面内阵型为谐波特性,在0~180 Hz内为柔性胎体与周向分布胎侧单元的同向振动,在180~300 Hz内为柔性胎体与周向分布胎侧单元的反向振动,基于柔性胎体-周向分布胎侧单元-轮辋耦合作用的试验模态首次揭示了重载轮胎的胎体与胎侧的耦合特征,将只分析胎体的0~180 Hz内的柔性特征,拓展为0~300 Hz的面内振动,为理论分析奠定了试验基础。
(2)基于弹性基础的柔性梁模型建立了重载轮胎的胎体-胎侧-轮辋耦合动力学模型,首次建立了轮胎几何、物理参数和胎体-胎侧-轮辋耦合模态的解析表达式,利用重载轮胎的试验和解析共振频率,利用遗传算法辨识重载轮胎的结构参数,并将试验模态结果与轮胎结构模型的解析解进行对比分析,预测误差在3%以内,同时模态的解析解可以预测试验无法测得的高频模态。
(3)通过模态解析解的分析,重载轮胎的胎体与胎侧的同向振动随着模态阶数的升高,收敛于特定值,而反向振动随着模态阶数的升高成指数增长,因此重载轮胎的高频振动形式主要变现为胎体与胎侧的反向振动。
[ 1 ] PAZOOKI A, RAKHEJA S, CAO D. Modeling and validation of off-road vehicle ride dynamics [J]. Mechanical Systems and Signal Processing, 2012, 28(2): 679-695.
[ 2 ] 左曙光, 冯朝阳, 吴旭东,等. 轮胎附着特性的胎体纵向振动建模与分析[J]. 振动与冲击, 2015, 34(10): 50-55.
ZUO Shuguang, FENG Zhaoyang, WU Xudong, et al. Tread’s longitudinal vibration modeling and analysis for attachment characteristics of tire [J]. Journal of Vibration and Shock, 2015, 34(10): 50-55.
[ 3 ] 赵愿玲,左曙光. 考虑驱动力影响的轮胎侧向自激振动分析[J]. 振动与冲击, 2012, 31(22): 101-111.
ZHAO Yuanling, ZUO Shuguang. Lateral self-excited vibration analysis for a type considering driving force [J]. Journal of Vibration and Shock, 2012, 31(22): 101-111.
[ 4 ] REINALTER W, RAUH J, LUTZ A. TMPT-conclusions and consequences for the industry from the industry [J]. Vehicle System Dynamics, 2007, 45(Sup1): 217-225.
[ 5 ] FAN C, GUAN Dihua. The quantitative analysis and experimental verification of the tire static enveloping model using experimental modal parameters [J]. Vehicle System Dynamics, 2006, 44(9): 675-688.
[ 6 ] 葛剑敏, 王卫防, 孙世铭, 等. 轮胎模态试验及在轮胎结构设计中的应用研究[J]. 轮胎工业, 2001, 21(4): 203-
207.
GE Jianmin, WANG Weifang, SUN Shiming, et al. Tire modal test and its application to tire structure design[J]. Tire Industry,2001, 21(4): 203-207.
[ 7 ] 高海慧, 陈剑. 轮胎振动特性实验研究[J]. 噪声与振动控制, 2011, 31(1): 175-178.
GAO Haihui, CHEN Jian. Experimental investigation of tire vibration characteristic[J]. Noise and Vibration Control, 2011,31(1): 175-178.
[ 8 ] 危银涛, 冯希金, 郑小刚, 等. 乘用车子午线轮胎泵浦噪声机理的实验-数值混合分析方法[J]. 振动与冲击,2015,34(11): 165-172.
WEI Yintao,FENG Xijin,ZHENG Xiaogang, et al. A hybrid experimental-numerical analysis for radial tire air pumping noise generation mechanism [J]. Journal of Vibration and Shock, 2015, 34(11): 165-172.
[ 9 ] MOHAMED Z, WANG X. A deterministic and statistical energy analysis of tyre cavity resonance noise [J]. Mechanical Systems and Signal Processing, 2016, 70/71: 947-957.
[10] MOHAMED Z, WANG X. A study of tyre cavity resonance and noise reduction using inner trim [J]. Mechanical Systems and Signal Processing, 2015, 50/51: 498-509.
[11] NA S D, PARK D W, YOO W S. Rigid ring with Bouc-Wen tire model for vehicle dynamic analysis [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 231(19): 3530-
3540.
[12] 危银涛, 刘哲, 周福强, 等. 考虑面外振动的轮胎三维环模型[J]. 振动工程学报, 2016, 29(5): 795-803.
WEI Yintao, LIU Zhe, ZHOU Fuqiang, et al. Three-dimensional REF model of tire including the out-of-plane vibration[J].Journal of Vibration Engineering, 2016, 29(5): 795-803.
[13] 左曙光, 毛钰, 吴旭东, 等. 基于柔性环轮胎模型的电动轮固有特性分析[J]. 振动与冲击,2016, 35(3): 41-47.
ZUO Shuguang, MAO Yu, WU Xudong, et al. Inherent characteristic analysis of the electrical wheel based on a flexible ring model[J]. Journal of Vibration and Shock, 2016, 35(3): 41-47.
[14] TROYER T D, GUILLAUME P, PINTELON R, et al. Fast calculation of confidence intervals on parameter estimates of least-squares frequency-domain estimators[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 261-273.
[15] KRYLOV V V, GILBERT O. On the theory of standing waves in tyres at high vehicle speeds[J]. Journal of Sound and Vibration, 2010, 329 (21): 4398-4408.
[16] VU T D, DUHAMEL D, ABBADI Z, et al. A nonlinear circular ring model with rotating effects for tire vibrations[J]. Journal of Sound and Vibration, 2017, 388: 245-271.
[17] BAGHERI M, JAFARI A A, SADEGHIFAR M. Multi-objective optimization of ring stiffened cylindrical shells using a genetic algorithm [J]. Journal of Sound and Vibration, 2011, 330(3): 374-384.

