基于双目视觉的呼吸运动实时跟踪方法研究

王 艳 孙向明 熊珀艺 王宇飞

(华中师范大学物理科学与技术学院，武汉 430070)

引言

随着放疗技术的不断发展，放疗效果有了明显提升。但在肿瘤放疗过程中，由呼吸运动所引起的肿瘤靶区的移位依旧是一个不可避免的问题。在放疗过程中如果不对该位移进行处理会导致周围正常的组织接受不必要的照射，严重影响其放射治疗效果，并且可能会导致不良反应的增加[1]。近年来，放疗工作者已采用多种方法以减少呼吸运动对肿瘤放疗的影响，Negoro 等[2]采用被动加压技术来限制肿瘤的动度，此方法虽简单易行但精确度差且不同患者间呼吸控制差异较大。传统采用呼吸门控手段的解决方案，Minohara等已利用此技术成功治疗了几百例肺癌和肝癌等患者[3]。患者在治疗中可以自由呼吸，但此项技术需要附加门控设备且硬件设备较复杂，由于人体呼吸运动复杂，难以保证肿瘤靶区运动与外部监控信号是否同步，无法保证治疗效果且同样能照射到正常组织。对比而言，通过实时跟踪肿瘤靶区组织的运动信息的技术硬件设备简单易操作，患者可自由呼吸且实时性强。

目前，实时跟踪肿瘤靶区放射治疗技术的方法[4]主要采用X光成像设备EPID对靶区进行实时监控、体外标记红外射线跟踪加正交X光成像(cyber knife(赛博刀))方法、实时影像跟踪等方式进行引导放射治疗。这些方法都能在一定程度上解决肿瘤靶区定位问题，但是在X光成像设备的治疗过程中并不是连续进行，延长了治疗时间，执行周期过长，严重影响其性能和患者的治疗效果。在目前的临床试验中，对于放疗定位应用较好的CyberKnife方法是实时跟踪患者靶区目标位置[5]。因CyberKnife设备价格昂贵，这对于中小医院难以接受[4]。相比之下，基于双目视觉的呼吸运动实时跟踪系统，以减少在胸腹部的肿瘤放射治疗过程中由于呼吸等因素造成肿瘤位置动态位移而引起的治疗误差的方法，患者呼吸自由，执行周期短，实时性、稳定性良好且硬件设备简单易于操作。本研究主要研究基于双目视觉的实时跟踪方式监控跟踪体表标记物动态信息。

1 方法

双目立体视觉是机器视觉的一种重要形式，它是利用左右成像设备获取被测物体的两幅图像进行立体匹配，根据匹配后得出的视差来获取物体三维几何信息。

在实际放射过程中，若基于单点的跟踪呼吸运动方法，只能判别出患者是否因呼吸运动使标记物发生位移，若采用基于多点的跟踪呼吸运动方法，会更加精确地判别出患者体表标记物是否发生位移，且知患者左右倾斜程度等运动情况，更有利于做出及时调整，使得到更好的肿瘤放射治疗效果。

双目立体视觉测量跟踪方法：运用两台标定好的摄像机设备获取被测标记物的两幅图像。对左右两幅图像进行标记物识别、标记物匹配、标记物排序、计算两幅图像中标记物的重心坐标，最后利用双目立体视觉计算出标记物在三维场景中的实际坐标。随着时间的变化，通过实时探测标记物在三维场景中的实际坐标，从而得知体表标记物的实时运动情况

1.1 跟踪目标图像识别与匹配

本研究采用基于多点的跟踪的方法，采用9个同规格的黑色矩形图来作为体表标记物。矩形标记物识别的基本原理：分别对拍摄的图像进行边缘检测[6]。边缘检测常用的一阶梯度算子[7]有Roborts、Prewitt、Sobel等算子，而最常用的二阶导数过零点检测的算法是由Marr和Hildreth提出的LoG[8]算子。虽然这些算子的计算量较小，但是这些梯度算子都是局域窗口，会在一定程度上丢失一些边缘信息，导致检测效果不理想。本系统采用Canny算子来进行边缘检测，利用John Canny的Canny算子[9]进行图像边缘检测，Canny算子是一种含有优化思想的算子，它具有较大的信噪比和较高的检测精度。利用Canny边缘检测算子和对Canny算法双阈值的设定对图片进行边缘检测提取轮廓。对提取的轮廓进行矩形标记物轮廓识别与匹配。

物体轮廓曲线经过数字化处理后会变成有序点集合。设A是需处理曲线上边缘像素点的集合，有

A={pi:(xi,yi),i=1,2,…,n}

(1)

需要先确定其构成余弦三角形的领域，有

Ω(pi)={pi-l,…,pi-1,pi,pi+1,…pi+r}

(2)

式中，Ω(pi)为点pi的支持领域，pi-l和pi+r分别为支持领域的两端端点。

Ω(pi)=[pi-l,pi+r]

(3)

且满足

‖pipi-l‖=‖pipi+r‖=U

式中，U为输入的参数且U>0，‖·‖表示两像素之间的欧氏距离，即

(4)

(5)

通过有序点坐标和输入参数U，确定领域两端端点pi-l和pi+r坐标，从而确定pi的支持领域如图1所示。

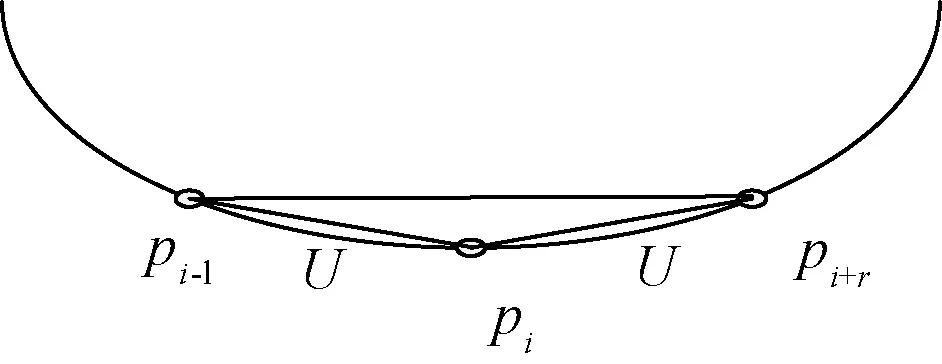
图1 pi支持领域Fig.1 Support region for pi

利用像素点pi坐标与其支持领域的两端端点坐标，确定像素点pi的夹角值。

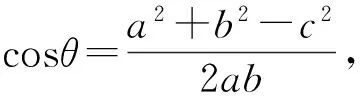
由于设定标记物为矩形，只需要考虑直角和直线情况。直角情形如图2所示，直线上的每个像素点的夹角值为零，直角处的像素点夹角值为90°左右。

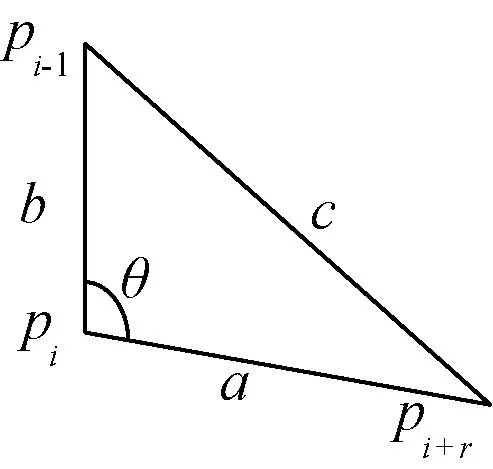
图2 余弦公式Fig.2 Cosine formula

对于得到的闭合轮廓，利用余弦公式计算得出夹角值。当闭合轮廓为矩形时，其夹角值为如图3所示，pxy为边缘线上的像素点。矩形有4个夹角值为90°左右的点。由于9个矩形标记物的长宽一致，把提取的轮廓均利用余弦公式计算后，进行夹角值循环匹配，本系统使用固定欧氏距离计算方法，具有很高的旋转稳定性和抗噪性，可进行旋转循环等操作匹配，增大匹配成功的几率，匹配出9个闭合轮廓一样的夹角值，即成功识别出9个矩形标记物。

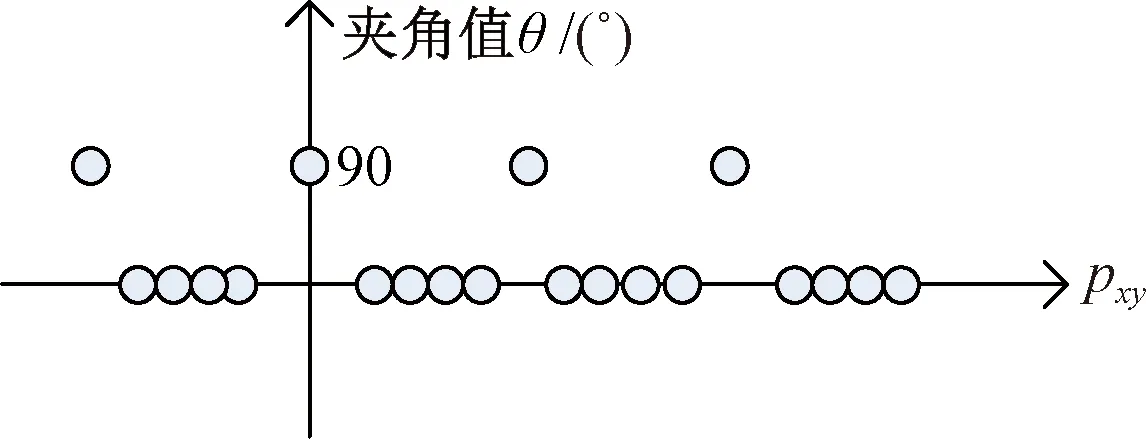
图3 单个标记物夹角值Fig.3 The angle plot of one marker

本系统采用基于多点的跟踪方法，多个标记物在未排序的情况不易于后期操作，无法得知具体哪个标记物的位移发生了怎样的变化，使9个标记物按照标准的3行3列的规则摆放于患者腹部体表，对标记物进行排序，每个标记物会有相应的序号，易于操作。

在理想状态下，标记物的摆放应是按照标准的3行3列的规则，但在实际操作中会存在一定的操作误差，需要处理和控制此误差。分别利用轮廓序列求取出每个矩形标记物轮廓的中心坐标，利用9个中心坐标求取出中点坐标，利用9个矩形轮廓的中心坐标与中点坐标之间的相互关系来进行排列。

在标记物被排序后，需要对左右成像设备获取被测物体的两幅图像进行匹配。设图像中每个标记物的中心点为匹配点。左右两幅图像分别会有9个匹配点。利用两幅图像的视差关系进行左右两幅图像匹配。设左右成像设备所拍摄的图像的0号标记物坐标的视差值分别为dixs、disy。xs数组即为左摄像机所拍图像的9个标记物的中心点分别与0号标记物的x坐标的视差差值。ys数组即为左摄像机所拍图像的9个标记物的中心点分别与0号标记物的y坐标的视差差值。

disx=x1[0]-x2[0];disy=y1[0]-y2[0];

xs[0]=x1[0]-disx;ys[0]=y1[0]-disy;

⋮

xs[8]=x1[8]-disx;ys[8]=y1[8]-disy;

根据视差基本原理，在理想状态下，有

disx1=x1[1]-x2[1];disy1=y1[1]-y2[1];

disx1=disx;disy1=disy;

同理可知：

xs[0]=x2[0]…xs[8]=x2[8]

ys[0]=y2[0]…ys[8]=y2[8];

由于在实际摆放标记物时存在一定的操作误差，本系统把误差接受范围设定为10个像素以内，即

abs(xs[1]-x2[1])<10;

abs(ys[1]-y2[1])<10

若两幅图像中的9个轮廓的中心点坐标满足此匹配条件，则左右成像设备获取被测物体的两幅图像匹配成功。左右图片匹配如图4所示。

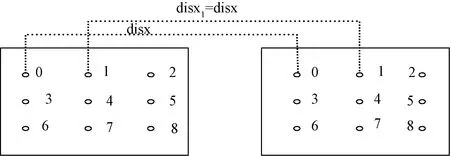
图4 左右图片匹配Fig.4 The picture of matching of left and right

1.2 双目视觉测量跟踪原理

利用单个标记物的重心为关键点计算在三维场景中的实际坐标。分别对每个标记物的轮廓扩大区域做掩膜处理，进行单个标记物图像的重心坐标提取。每幅图像提取9个重心坐标为关键点以供双目立体视觉测量时使用。图5是采集100次单个标记物的重心点坐标。

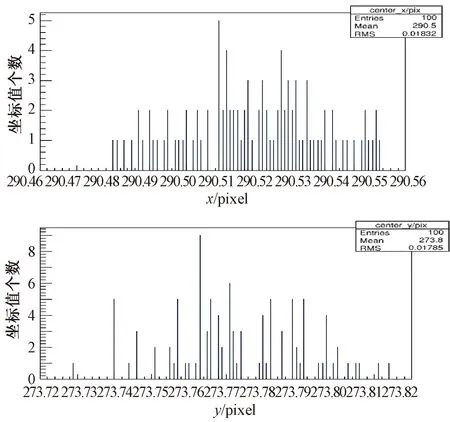
图5 一个标记物重心坐标Fig.5 The center of gravity y coordinate of one marker

由图中得知，重心点x、y坐标值的均方根误差在1/50个像素左右很稳定。

双目立体视觉测量基本原理：依据小孔成像的基本原理，左右摄像机可以建立坐标系，图6为双摄像机模型二维图，图7为双摄像机模型立体视图。其中，p点是被测物体，f为两摄像机的焦距，p1、p2是被测物体p在左右摄像机的像平面上所成的像点，xl、xr分别是p1、p2在像面上的x坐标，Ol、Or分别是左右摄像机的光心，D为两摄像机之间的距离，z为被测物体p与两摄像机平面间的距离。

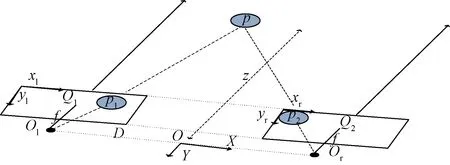
图6 双摄像机模型二维图Fig.6 Two-dimensional map of the model of binocular

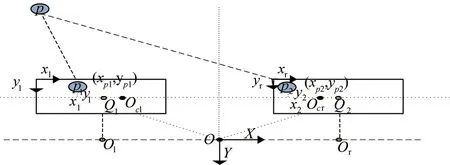
图7 双摄像机模型立体视图Fig.7 Dimensional view of the model of binocular

由相似三角形原理可知被测物体p的深度z。由于D和f是已知的，从得出深度距离z的公式可知，分别测出xl和xr即可得出深度距离z。由相似原理可得出△pp1p2与△polor相似，则

(6)

在图6、7中，(x1,y1)、(x2,y2)分别是p1、p2相对于成像面中心点Q1、Q2的x、y坐标。(xp1,yp1)、(xp2,yp2)分别是p1、p2在像面上的坐标。Q1、Q2分别是左右摄像机像平面的中心点。d为左右摄像机像面上像中心Q1与Ocl的距离与Q2与Ocr距离之和。由小孔成像基本原理可知，y1与y2相等。Oc点与目标物体p点映射在左右摄像机的像面分别是p1Ocl和p2Ocr，由小孔成像原理可得

p1Ocl=p2Ocry1=y2⟹x1Ocl=x2Ocr

(7)

列出等式，有

xp1Q1+Q1Ocl=xP2Q2-OcrQ2⟹

Q1Ocl+OcrQ2=x2Q2-x1Q1

(8)

又由于

Q1Ocl+OcrQ2=x2Q2-x1Q1=d

(9)

xp1-xp2=d

即得出

(10)

计算得三维坐标值为

Y=(yp1-yQ1)r

(11)

Z=fr

1.3 实验方法

实验硬件由两个已标定好的摄像头放置于治疗床上方，进行患者胸腹部标记物图像采集与一台PC机组成。为了便于使用同时开发了一套实验软件系统，用于完成图像采集、标记物识别、匹配和三维坐标的实时计算等工作。实验中，选取9个矩形标记物规格放置在平躺人体腹部，利用软件系统实时获取9个标记物的实时三维坐标，并动态显示数据结果(摄像机采样频率为10 Hz)。

2 结果

根据试验记录，前100帧测试数据如表1所示，记录了9个标记物在100帧图片中通过系统测量出的三维坐标与实际三维坐标值的平均值与误差值。在表1中，x表示标记物的左右运动方向，y表示标记物对应于人体头脚方向的运动方向，z表示标记物对应于腹部上下运动即运动深度方向。Mean表示坐标平均值。RMS表示坐标均方根误差值。9个标记物产生位移的100帧数据如表2所示，在移动过程中会改变被测物体的光照强度。表2中Mean表示标记物在未移动前坐标的平均值，Mean-n表示移动后坐标的平均值。同理，RMS-n表示移动后的坐标均方根误差值。

表1数据显示系统测量值与实际值的平均误差小于±1 mm。均方根误差值均小于0.12 mm。

表2数据是在标记物发生位移后采集的数据。通过对比移动前后平均坐标值可知，1号标记物在x坐标方向移动0.104 cm，y坐标方向移动0.14 cm，z坐标方向移动0.95 cm。各个标记物坐标的均方根误差值并没有因移动而受到影响。标记物的三维坐标的均方根误差值均小于0.12 mm，此方法标记物移动过程中探测精度并没有发生变化，性能较稳定。通过表2中9个标记物移动后的数据显示腹部靶区均向右下方移动，且处于吸气状态。在整个放疗过程中当患者处于稳定状态，且已定位好放疗靶区设置当前的标记物坐标为初始坐标，当每次重新调整靶区位置时则更新初始坐标。通过9个标记物实时坐标与初始坐标可知9个标记物的运动轨迹，且能分别得出9个标记物的移动倾斜角度，例如将表1中0号标记物未移动前的位置设置为初始位置，通过表1的位置可得0号标记物的x-z方向倾斜角度为84.3°,y-z方向倾斜角度为82°且通过3个轴方向的移动精确得知9个标记物的运动轨迹，从而判别出患者的移动方向与倾斜角度以便及时调整。数据表明系统同时追踪9个标记物时，其测量结果仍具有较好的稳定性与精度，且基于多点标记物跟踪能更好、更多地获取患者移动的体表信息。

表1 实验数据1

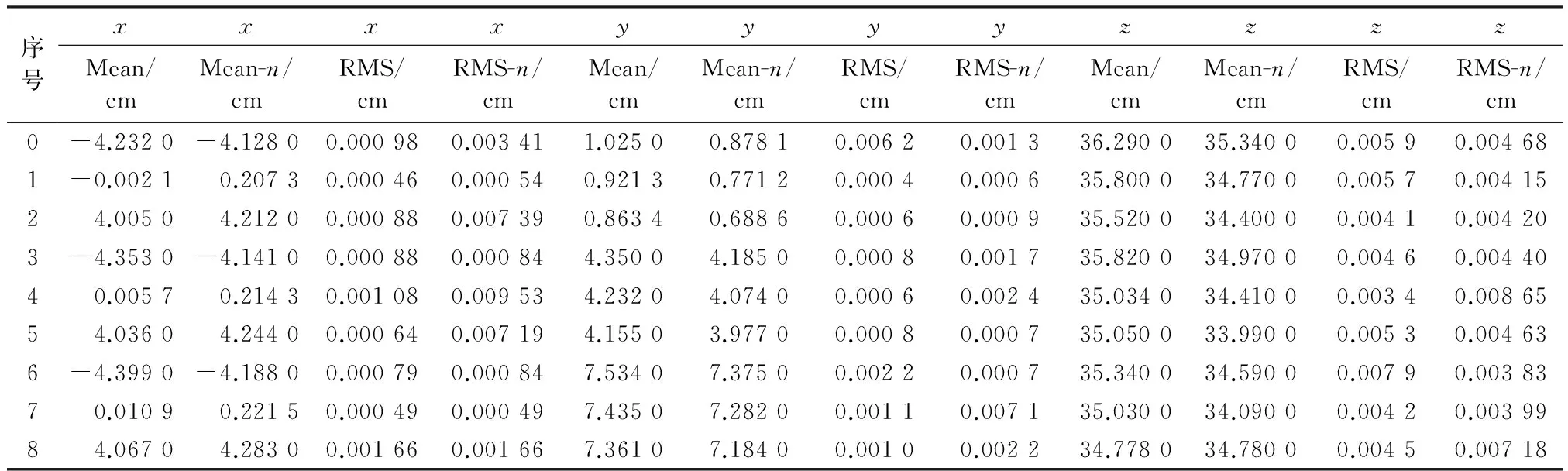
表2 实验数据2

3 讨论

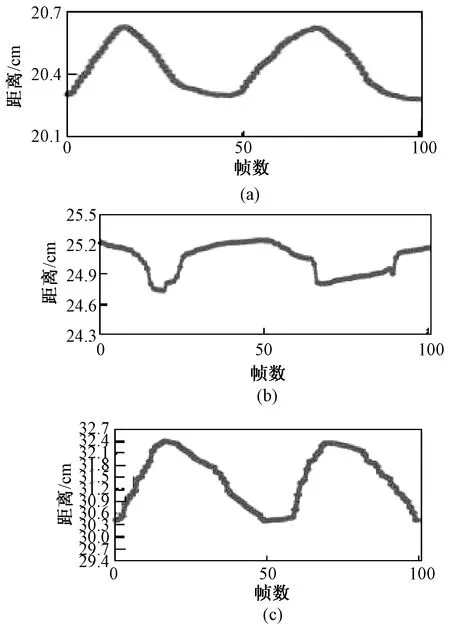
图8 位置跟踪(帧/s)Fig.8 The position of tracking (frames/s)

实验中，每一帧单个矩形标记物处理时间为10 ms，每一帧9个标记物处理时间为35 ms，相对于朱超华等研究利用SIFT特征匹配方法处理时间上较优化[12]。由于成人正常呼吸周期为3～5 s[13]，呼吸频率为12～20次/min，能满足实时性。图8是对一个标记物进行实际测量的3个轴上的位置与时间跟踪。其中，(a)～(c)分别表示x、y、z方向位置跟踪图，3个轴上的轨迹均有改变，z轴位移变化较明显，因为标记物放置于患者腹部。Bradley等对肺部肿瘤的运动进行了一项研究，表明肿瘤单一方向运动最大可达3 cm，实验中z轴运动为上下2 cm左右，测量精度稳定在1/50个像素，达到放疗精度要求[14]。Yilmaz等研究指出，基于图像的目标跟踪主要有以下几个较复杂方面：是否出现图像信息丢失、图像噪声、目标物体的部分遮挡、光照变化与实时性要求[15]。在实验中，是直接由2D图像中的坐标信息进行计算三维坐标，避免了图像信息丢失，实验中利用固定欧氏距离确定支持领域来增大图像的旋转稳定性与降低噪声的影响。利用视差匹配方法，解决光照等问题。实验结果表明，系统能解决目标物体的旋转、光照等问题。基于多点跟踪方法虽然能获取患者更多的运动体表信息，且保持着较好的实时性、稳定性与较好的测量精度，但在实际放疗过程中，位于胸腹部的肿瘤会有着不同的体积大小、不同的运动模式与不同的位置，系统目前只考虑了体表标记物在呼吸运动影响下的情况，还无法完全匹配出体内靶区的呼吸运动情况。下一步的工作需要进行系统改进，使体内肿瘤靶区与体外标记物两者之间进行模型匹配，使两者之间有精确的对应关系。

4 结论

采用基于多点跟踪呼吸运动方法实现基于双目的肿瘤靶区标记物的三维跟踪，不仅能获取患者更多的运动体表信息，而且保持着较好的实时性、稳定性与较好的测量精度，可减少呼吸运动对精确放疗产生的影响。在实际呼吸运动中，肺部、胰腺、肝脏和其他胸腹部的肿瘤均会随呼吸运动产生位移[16]。因此，还需考虑胸腹部靶区与标记物更具体的对应关系，从而更好地为放射治疗过程中肿瘤的移位提供实时跟踪。

[1] Starkschall G, Forster KM, Kitamura K, et al. Correlation of gross tumor volume excursion with potential benefits of respiratory gating[J]. Internation Journal of Radiation Oncology Biology Physics, 2004, 60(4): 1291一1297.

[2] Negoro Y, Nagata Y, Aoki T,et al. The effectiveness of an immobilization device in conformal radiotherapy for lung tumor: reduction of respiratory tumor movement and evaluation of the daily setup accuracy.[J] Internation Journal of Radiation Oncology Biology Physics, 2001,50(4):889-898.

[3] Miohara S,Kanai T,Endo M,et al.Respiratory gated irradiation system for heavy-ion radiotherapy[J].Internation Journal of Radiation Oncology Biology Physics,2000,47(4)：1097-1103.

[4] Kini VR, Vedam SS, Keall PJ, et al.Patient training in respiratory-gated radiotherapy[J].Med Dosim,2003,28(1):7-11.

[5] 伍锐,陈超敏.肿瘤靶区呼吸运动实时反向跟踪系统在精度放疗中的应用研究[J].南方医科大学学报, 2010,30(1):100-102.

[6] Gonzalez RC, Woods RE. Digital Image Processing(3rd Edition)[M]. Beijing: Beijing Publishing House of Electronics Industry,2011:445-465

[7] Heath M,Sudeep S,Sanocki T, et al. Comparison of edge detectors.A Methodology and Inital Study[J].Computer Vision and Image Understanding,1996,68(1):38-54.

[8] Marr D,Hildreth E.Theory of edge detection[J].Processings of the Royal Society of London Series B,Biological Science,1980,207(1167):187-217.

[9] Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(6):679-698.

[10] 钟宝江,廖文和.基于精化曲线累加弦长的角点检测技术[J].计算机辅助设计与图形学学报,2004,16(7):940-943.

[11] 郭娟娟,钟宝江.U弦长曲率：一种离散曲率计算方法[J].模式识别与人工智能,2014,27(8):683-691.

[12] 朱超华,陈武凡,徐子海,等.基于双目视觉的呼吸运动实时跟踪方法研究[J].中国生物医学工程学报,2011,30(4):520-526.

[13] 万学红,卢雪峰. 诊断学[M].北京：人民卫生出版社,2013(3):128.

[14] Jeffrey D,Bradley MD,Perez, MD,et al.Implementing biological target volumes in radiation treatment planning for nom-small cell lung cancer[J].The Tournal of Nuclear Medicine, 2004, 45(Suppl 1): 96S-l01S.

[15] Yilmaz A,Javed O,Shah M.Object tracing:A survery[J].Acm Computing Surveys, 2006,38(4): No.13.

[16] Berbeco RI, Nishioka S, Shirato H,et al.Residual motion of lung tumors in end-of-inhale respiratory gated radiotheraphy based on external surrogates[J]. Medical Physics, 2006, 33(11):4149-4156.