青海省藏汉双语高中生三角函数解题错误层次调查研究

才让加

【摘要】学生在学习数学的过程中，在某种程度上会不可避免的出现解题错误，但是在学习过程中我们又希望学生能够很好地掌握相应的知识，提高数学能力，从而降低解题错误。三角函数是高中数学的重要内容之一，它既能联系代数又能联系几何，可将复杂的数学问题简单化，因此，研究学生在学习三角函数过程中出现的错误，对其进行归类，并分析其形成的原因，具有很重要的意义。从目前的研究资料来看，研究关于藏汉双语高中生三角函数解题错误的文献很少，因此笔者编制了三角函数测试卷，对青海省六州藏汉双语高中生三角函数解题能力进行了测试，按解题的一般顺序——阅读、理解、转换、操作、编码中出现的错误程度进行了统计，进而用SPSS 20.0对数据进行了分析，得出藏汉双语高中生在解决三角函数问题时，出现的错误层次以理解、编码、操作、阅读、转换而递增，未能成功解题的主因在于不能把文字转换成数学模型，不能选取合适的解题策略。

基于以上研究结论，笔者反思了青海省六州民族高级中学的数学教学状况，特别对藏汉双语三角函数教学提出了几点建议。

【关键词】藏汉双语 三角函数 解题错误 研究

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2018）06-0125-02

一、研究的背景及问题

函数的思想深刻、应用广泛，是高中教学内容的核心部分，其与数列、方程、导数、几何，以及不等式等内容相互渗透，且函数的思想渗透在整个高中的全部过程中。而三角函数又是一类特殊的函数，历来是高中数学的重要内容之一，也是学生在高中阶段必须掌握的基本初等函数。

在藏汉双语教学过程中，以教学质量而言提升的幅度是非常的缓慢。尤其是学生在学习三角函数这一内容时，经常会遇到很多问题，常常会出现解题错误。那么青海省藏汉双语高中生的数学成绩难于提高的主因在哪里？特别是学生在学习三角函数时出现的错误是什么？因此探索藏汉双语高中生在三角函数学习过程中存在的问题，并分析其产生的原因，就显得尤为重要。

学生在解決问题时出现错误是有一定的合理性的，如果积极和科学地分析其合理之处，变可有“化腐朽为神奇”的效果，分析其出现的原因、性质，逐步“将错为正”，将“正确”建立在“错误”之上，相信同学们对原先错误的解题和现在正确的解题都有很深刻的理解。

错误在哲学中定义为：错误同正确对立，是指主体与客体规律不相一致的认识或实践，显然，此处的错误是一种不正确的观点和行为。错误不仅在哲学中出现而且在其他学科，以及在日常生活中也会出现。在《现代汉语词典》中将错误解释为不正确的，与客观事物不相符的思想，或者是不正确的行为、事物等。

错误在数学教育中，由于数学本身的特点，没有人直接对数学错误给出了直接的定义，但对错误有一些简单的论述：郑毓信在《数学教育的现代发展》一文中有这样的论述：有些教师将学生在具体的学习过程中产生的不同于“标准观念”的想法或做法视为错误。此处的“标准观念”指的是教材、专家及自身的观念。Brousseau不认为错误是失误或偶然的现象，而是对前知识的学习发生兴趣的表现。

二、国外对高中生三角函数解题错误研究的综述

国外对学生的解题错误是从学生算术错误的诊断开始入手的，早在1925年美国学者buswell与judd用了长达30多年的时间对学生的算术错误进行诊断，其后，德国和苏联等国家也相继加入了此研究的行列。

传统的观点认为，错误是没有任何益处的，学生犯错也就意味着其成绩是不理想的。如skinner认为应该避免错误，因为错误会浪费其完成任务的时间。但随着学者们对错误的不断研究，逐渐认识到错误不仅可以加深学生对数学知识的理解，而且教师也可纠正自己的教学方法。如Borasi认为学生在学习的过程中所出现的解题错误是对其已有认知结构的再调整的结果，所以教师可以通过学生的思考及错误的解题，从而可以提供一条更有效的补救方案。

亨德里克思从心理学的角度对学生的错误进行了研究，总结出学生犯错的原因有语言困难、空间想象力不足、已有知识经验的不足、思维定式的影响、不恰当的应用或推广等五个方面。

澳大利亚的心理学家纽曼（Newman）针对一步计算的文字题于1977年提出把学生的解题错误按解题过程分成以下五个层次：①阅读能力；②理解；③转换；④运算技能；⑤呈现答案（见表1）。

Watson在1980年发表的《Investigating errors of beginning mathematicians》中认为纽曼（Newman）的错误分析理论适用于大量的数学问题，该错误分析理论是建立在学生是如何解答数学问题的一个合理的数学模型的基础上，此模型在不同的解题阶段出现的解题失败表现出不同的解题错误。此后很多研究者将纽曼（Newman）错误分析理论应用到各个领域。Ellerton对206名初中生在解决数学文字题的困难类型做了调查，得出了70%以上的同学出现的解题错误来源于理解题意错误和选择解题策略错误。

纽曼（Newman）的错误分析理论比较成熟、完善，借鉴的研究成果也比较多。如Clarkson、Prakitipong& Nakamura、Zakaria&Maat;、黄兴丰和郝玲等在研究中应用了纽曼（Newman）解题错误分析理论。

三、国内对高中生三角函数解题错误研究的综述

数学是在问题解决的过程中产生的，并且也是在解决问题的过程中完善和发展起来的。我国历来对解题教学很重视，很多学者在这方面有着很深的研究。如单墫教授所说的“数学的习题，不仅用来巩固所学的知识，还可以培养能力，发展智慧。所以，通过解决问题，能够更好地掌握数学的内容、意义和方法 。”

戴再平在《数学习题理论》中认为，在数学的解题中，学生所表现的错误是多样的，为了更有效地利用好这些错误，必须对各种错误进行归类和分析，但由于产生错误的原因和复杂程度，以及错误表现形式的多样性，因此要有不同的标准对错误进行不同的分类。并将错误分为阅读理解、转码、加工技能、策略选择、编码五种。

向正凡在《辨析中學生数学解题错误与培养数学解题能力的研究》一文中把数学解题错误分为曲解题意的错误、拟定方案的错误、执行方案的错误、回顾与反思的错误四类。

黄兴丰在《初中生在几何解题中所出现错误的调查研究》一文中把解题中发生的错误分为阅读理解、转码、加工技能、策略选择、编码五种。

王志英在《普高学生数学解题错误的成因分析与对策研究》一文中将学生在解题过程中出现的解题错误分为心理性错误、概念理解性错误、运算性错误、审题性错误、逻辑性错误。

魏述强在《基于学生错误的试卷讲评模式的行动研究》一文中以纽曼（Newman）错误分析理论为基础，结合自身的教学经验将学生在解决解析几何题时可能出现的错误分为阅读理解错误、选择解题策略错误、数学转换错误、技能加工错误、数学编码错误。

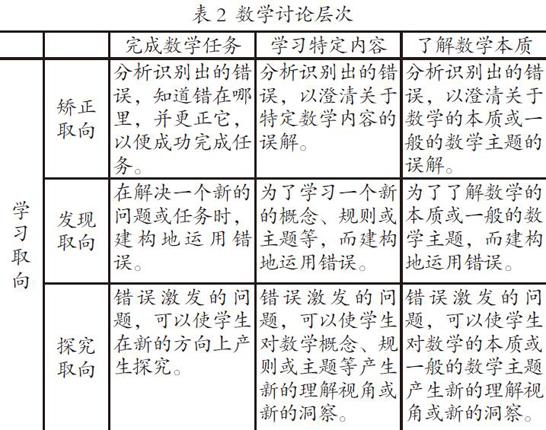
表2表示Borasi在1989年将错误进行分类，Borasi认为在分析学生的错误时，可以提供机会使学生进行优异的数学活动；通过识别错误，可以强调新的方面或解释意外的元素；关注和处理错误的经历可以使学生在今后的数学活动中更为谨慎，能够对作业的正误进行核对等作用。Borasi对数学学习的错误，以及对错误分析的观点与看法是新颖与深刻的。

从以上国内外学者对解题错误的研究来看，不仅对研究的领域在不断的扩大，而且对解题错误的理解以及出错原因的认识也在不断地变化。更多的教师意识到解题错误不仅仅是对学生的“诊断”和“治疗”，更应将其视为一种教学资源，总之，学生的解题错误值得我们去研究，尤其是导致学生出错的原因和价值更值得我们去深入的探讨。

四、藏汉双语教学现状综述

才科扎西在《甘青川三省藏汉双语数学教学现行模式评述》一文中指出藏汉双语教学模式有两种，第一模式为本民族语言文字授课为主，单科加授国家通用语言文字，第二模式为国家通用语言文字授课，单科加授本民族语言文字。

才果在《青海藏区藏汉双语教学发展与思考》一文中认为青海民族教育的难点是藏族教育，而藏族教育的难点又在于藏汉双语教育。该文对青海藏区双语教育提出了建立藏汉双语民族幼儿园、高考中增加藏汉双语招生人数、大力发展藏汉双语职业教育、大力培养藏汉双语理科师资、加大投入藏汉双语教育的经费等五点建议。

索南仁欠老师在《青海藏汉双语教学现状及建设》一文中从教学模式、师资队伍、教材建设等方面对青海省藏汉双语的教育现状进行了总结，并认为应科学地定位双语教师的培养目标、优化双语教师的培养层次、科学地推进双语教材的建设进度、完善双语教师的评估体系、完善双语教师的培训等建议。

扎洛老师在《制约少数民族双语数学教育质量的主因分析》一文中人深入地探讨了制约青海少数民族双语教育质量的主因是双语教师的学科专业素质，教师素养成为提升藏汉双语教育教学质量的瓶颈。

从以上各位学者的研究来看，不难发现，关于藏汉双语的研究主要集中在大的方向，而对藏汉双语教学中每个学科比如：数学、物理、化学等方面的研究甚少，特别是对中学数学中各个模块的研究更是少之又少。进而学生在学习三角函数时会出现那些错误？在解决关于三角函数的问题时，学生会应用哪些知识模块？在解题过程中思维出现障碍时，会做出怎样的反应等方面的研究是非常的少。

五、研究目的、对象及方法

通过研究青海藏区六州藏汉双语教学高中生在学习三角函数这一内容时所存在的解题错误和出现这些错误的原因，以此来抛砖引玉，吸引更多的研究者来研究这一问题，进而提出改进教师的教学策略，以及提高学生的解题及自我反思能力，从而提升学生的数学解题能力。

青海省共有六个藏族自治州，根据青海省教育的布局调整，初步形成了村办幼儿园、乡办小学、县办初中、州办高中的状况，本研究选取的调查对象是青海省藏区六州每州一所民族高中，含盖了所有的藏族自治州，覆盖面100%，样本具有较好的代表性。本次测试卷共发放521份，回收500份。测试卷作答时间为90分钟。

本研究所采用的是测试卷的调查方式，测试卷分为藏汉两个版面并进行了双语对照，并用SPSS（20.0）数据软件统计、分析、处理问卷的数据与结果。

六、研究的结论及建议

1.研究的结论

（1）样本数据的相应分析

对于本次测试的数据笔者应用spss（20.0）进行了相应分析，得出：青海藏区双语教学高中生在解决三角函数问题时，解题错误以理解、编码、操作、阅读、转换的顺序而递，即：未能成功解题的主因在于不能把文字转换成数学模型，不能选取合适的解题策略。

（2）区间段数据的相应分析

对于青海省藏汉双语教学高中生在解决三角函数问题时出现的错误，笔者根据测试情况，将其分为十个区间，即：[0，10]、[11，20]、[21，30]、[31，40]、[41，50]、[51，60]、[61，70]、[71，80]、[81，90]、[91，100]具体统计情况如下：

1）成绩处于[0，50]的高中生在解决三角函数问题时，在阅读这一环节没有过关，即：没能辨别关键的字词和符号成为不能把问题正确地解决的关键。

2）成绩处于[51，90]的高中生在解决三角函数问题时，错误主要出现在理解这一过程，即：能够阅读问题但不能准确理解关键字词、符号和问题的真正含义，从而出现错误。

3）成绩处于[91，100]的高中生在解决三角函数问题时，解决问题的错误以理解、阅读、转换、编码、操作为序而递增，即：没能将问题成功地解决的关键在于能够找到一个合适的解题策略，但不能正确地进行数学操作。

2.建议

成绩处于[0，50]的学生在解题过程中阅读错误的秩均值偏高，由于阅读是基础，基础不牢，山动地摇，出现阅读错误而不能辨别关键的字词和符号，进而不能理解关键字词、符号和问题的真正含义，即出现理解错误，所以导致转换、操作等一系列错误，这就要求数学教师在以后的数学教学过程中不仅要讲透数学专业知识而且要讲清数学关键词和关键术语，指导学生经常阅读数学读物，提高学生的阅读能力。成绩处于[51，90]的学生在各个解题过程中呈现的秩均值偏高的理解，虽然能够阅读问题，但理解出现偏差，不能准确理解关键字词、符号和问题的真正含义，这就要求教师加强培养学生的数学抽象、推理、模型等基本数学思想，以培养学生的理解能力。成绩处于[91，100]的学生在各个解题过程中呈现的秩均值偏高的是操作，由于出现操作错误，所以学生在解题过程中能够找到一个合适的解题策略，但不能正确地进行数学操作，从而出现解题错误，这就要求教师经常指导学生注意整理、归纳解题方法，进而提高学生的运算操作技能。

参考文献：

[1] 王志英.《普高学生数学解题错误的成因分析与对策研究》[D].杭州师范大学硕士学位论 文.2012.

[2] 霄肖. 《初中生函数应用题解题障碍的研究》[D].西南大学硕士学位论文.2014.

[3]（中国社会科学院语言研究所词典编辑室.现代汉语词典（2002年增补本）[M]. 北京：商务印书馆.2004）.

[4] 郑毓信.《数学教育的现代发展》[M]..江苏教育出版社.1999

[5] 陈志云.纠正高中生数学解题错误实验研究[D].华中师范大学硕士论文.2008.

[6] Borasi，R.（1989）.Students Constructive Uses of Mathematical Errors： A Taxonomy， Paper Presented at the Annual Meeting of the American Educational Research Association（SanFrancisco，CA，March27-31，1989，ERIC：ED309069.） .