关于Birkhoff逆问题中Santilli方法的研究∗

崔金超 陈漫 廖翠萃

1)(江南大学理学院,无锡 214122)

2)(北京理工大学机械与车辆学院,北京 100081)

(2017年9月21日收到;2017年11月21日收到修改稿)

1 引 言

Lagrange逆问题、 Hamilton逆问题以及Birkhoff逆问题,是动力学逆问题研究的主要对象[1−3].Douglas[4]和Havas[5]关于Lagrange逆问题的研究表明,只有自伴随的牛顿系统或完整约束力学系统能够Lagrange化.运动微分方程不满足Helmholtz条件的本质非自伴随系统,不能Lagrange化,因此Lagrange逆问题对于完整约束力学系统而言不具有普适性.再由Lagrange方程和Hamilton方程的等价性可知,Hamilton逆问题也不具有普适性[6,7].于是提出了一个问题:在分析力学范畴内,是否存在一种自伴随的动力学模型,其逆问题对于完整约束力学系统来说是普适的?

20世纪80年代物理学家Santilli[8]对这一问题的深入研究表明,对于满足局部性、解析性、正规性基本条件的完整约束力学系统,普适的自伴随动力学模型是存在的,其解析表达就是Birkhoff方程形式.Birkhoff方程是Hamilton方程的自然推广[9−15],它将非保守系统的几何特性表现为一般辛结构,而不是Hamilton方程那样的简单辛结构.这种更为一般的辛结构,为非保守系统保结构算法的研究提供了几何基础[16−22].因此,寻求完整约束系统的Birkhoff表示,亦即研究Birkhoff逆问题显得尤为重要.

Birkhoff动力学的逆问题主要研究力学系统能够表示为Birkhoff方程形式的条件,以及Birkhoff动力学函数的构造方法.但完整非保守系统的广泛性和复杂性,导致Birkhoff动力学函数没有像Lagrange函数和Hamilton函数那样简单的构造方法.国内外关于这一问题的研究成果屈指可数[23−26],现有构造方法主要是Santilli[8]提出的,分别为利用偏微分方程的可积性定理直接构造Birkhoff动力学函数的Santilli第一方法,利用自伴随因子的函数积分法即Santilli第二方法,以及借助给定系统首次积分的Santilli第三方法.上述三种方法在具体应用中还有许多技术性问题需要解决.例如在Santilli第一方法中,如何从欠定的偏微分方程组中解得所需的Birkhoff动力学函数.文献[9]针对自治系统情形中的这一问题提出了能量赋值法,通过将系统的总能量取为Birkhoff函数,然后再求解Cauchy-Kovalevskaya型正定方程组来解决这一问题;文献[23]则通过增加一个附加方程,将原来欠定的方程组化为正定方程组来求解.Santilli第二方法应用的技术性困难在于必须先将系统自伴随化,而这一前提通常较难满足.文献[24]针对已经自伴随化的一类系统,提出了简化的Santilli第二方法,指出了一个被人们长期忽视的冗余项问题.Santilli第三方法的使用困难有两个,一是要求系统全部第一积分为已知,二是对于多自由度系统的计算繁琐.

近年来,我们针对上述问题开展了一些研究工作.本文将在前期工作基础上给出一些新成果.第2节将从笛卡儿坐标系下的达朗伯原理出发,介绍完整系统在广义坐标系下的一阶标准形式,然后介绍Birkhoff方程及其逆问题;第3节具体介绍Santilli提出的三种构造方法;第4节分别介绍这三种方法的研究进展,包括Santilli第一方法的拓展研究,Santilli第二方法的简化证明,Santilli第三方法的改进及其MATLAB程序化计算;第5节总结全文并对结果进行讨论.

2 Birkhoff方程及Birkhoff逆问题

考虑笛卡儿坐标系中由N个质点组成、受有3N−n个完整约束的力学系统,其运动微分方程由D’Alembert原理描述为

这里及以下采用爱因斯坦求和约定.

引入广义坐标qi(i=1,2,···,n),并利用坐标变换关系rk=rk(t,q)得到完整约束力学系统((1)式)在位形空间中的表达式,

由于上述二阶微分方程有可能是本质非自伴随的,因而不宜作为逆问题普适性理论研究的出发点.为此,采用文献[8]的降阶方法得到与(2)式等价的一阶标准形式

再结合下述定理,则可在Birkhoff力学体系下建立普适的自伴随方程.

定理1任何局域、解析、正规、完整的一阶力学系统((3)式),在其正规点的星形邻域上,总能实现自伴随的、保持动力学函数物理意义和变量实验室可测性质的Birkhoff方程形式,即

式中B(t,a)称为Birkhoff函数,2n个函数Rµ(t,a)称为Birkhoff函数组.

为方便起见,将2n+1个函数(B,Rµ)统称为Birkhoff动力学函数,再引入Birkhoff张量

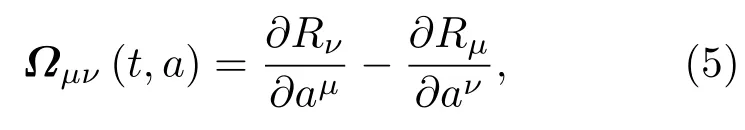
则(4)式可写为

进一步,若(6)式中函数和都不显含时间,则(6)式成为自治Birkhoff方程,即

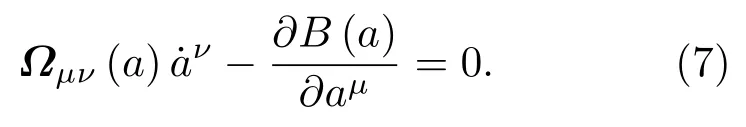
容易验证Birkhoff方程满足如下自伴随条件:

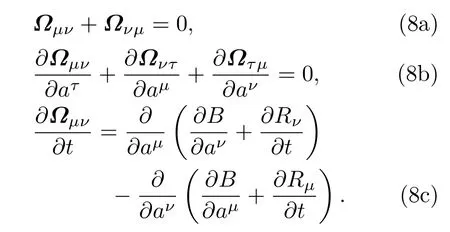
于是,Birkhoff逆问题可以具体阐述为:构造未知函数B和Rµ,使得完整约束系统的运动微分方程((3)式)与Birkhoff方程((4)式)等价,即

亦即要求

并且同时满足自伴随条件((8)式).

3 构造Birkhoff动力学函数的Santilli方法

Santilli第一方法. 对于给定的Birkhoff函数B,(10)式是关于Birkhoff函数组Rµ的Cauchy-Kovalevskaya型方程,即

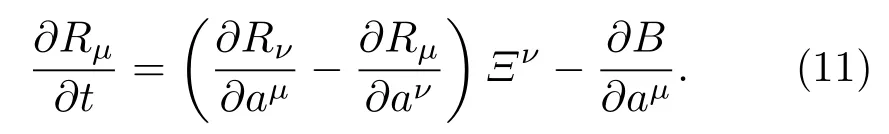
由Cauchy-Kovalevskaya定理可知,(11)式的解Rµ总是存在的.因此,如果能从(11)式解得一组Rµ,就能找到所需的Birkhoff动力学函数.这种方法称为Santilli第一方法.

在实际应用中,若已知系统的总能量(即动能与势能的和),则将其取为Birkhoff函数B,那么理论上通过求解(11)式就可以确定Birkhoff函数组Rµ.但对于一些复杂的力学系统,(11)式未必能够顺利求解,因而限制了Santilli第一方法的实效性.

Santilli第二方法.设系统的一阶标准形式((3)式)已自伴随化为如下形式:

式中下标SA表示自伴随(self-adjointness),为变量t,a的一般函数.此时Birkhoff张量Ωµν为已知量,将其代入Birkhoff张量的定义((5)式)直接积分得

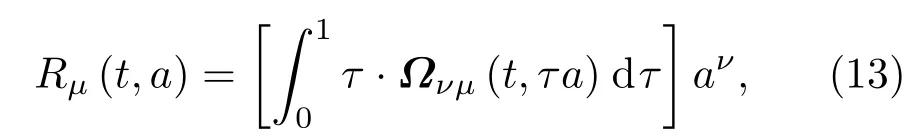
式中τ是参变量并且满足0≤τ≤1.将求得的Ωµν和Rµ代入Birkhoff方程((4)式),并注意到(12)式,则可得

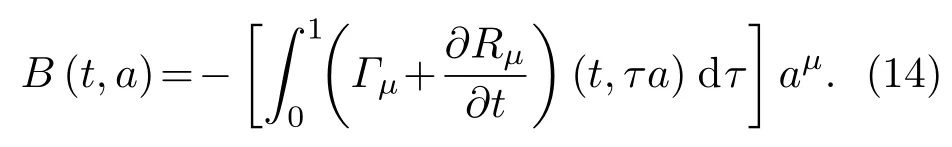
这种方法称为Santilli第二方法.

Santilli第三方法. 若已知系统((3)式)全部独立的第一积分Iα(t,a)(α=1,2,···,2n), 则Birkhoff动力学函数可由下式确定:

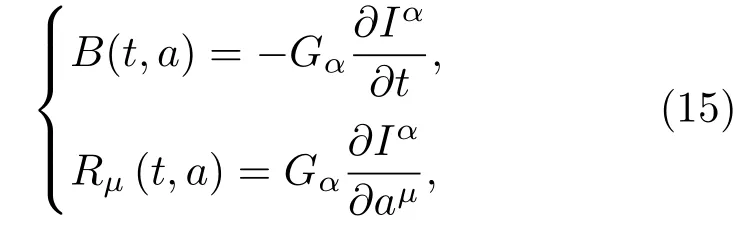
式中函数Gα=Gα[I(a)]要满足正规性条件

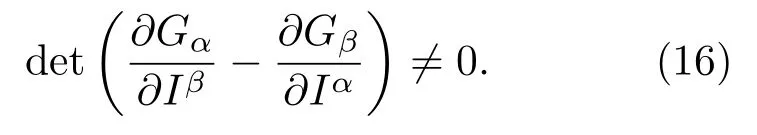
这种方法称为Santilli第三方法.

4 Santilli方法的研究新进展

4.1 Santilli第一方法的拓展研究

文献[9]关于Santilli第一方法在自治系统中的应用,启发我们思考如下问题:自治系统((3)式)是否总有自治Birkhoff表示((7)式)?文献[8]对这一问题有所讨论,但没有给出具体证明.这里采用反证法加以证明.

命题1自治系统总存在自治Birkhoff表示.

证明假设某个自治系统

不存在自治Birkhoff表示,即对向量场Ξν找不到B和Rµ使得等式

成立.但另一方面,存在B(a)使得(18)式总是Cauchy-Kovalevskaya型的,只需将B(a)=RνΞν代入(18)式整理得

显然,这是一组以2n个Rµ为未知函数的2n个一阶偏微分方程组.不妨假定则(19)式可写为Cauchy-Kovalevskaya型方程

由Cauchy-Kovalevskaya定理知(20)式的解总是存在.这说明对任意给定的向量场Ξν总有(18)式成立,这显然与假设矛盾.故自治系统总有自治Birkhoff表示.证毕.

4.2 简化的Santilli第二方法

对于已经自伴随化的力学系统,用Santilli第二方法构造Birkhoff动力学函数是方便的.但长期以来,人们忽视了该方法中存在的冗余项,造成求解过程繁琐复杂.在文献[17]中我们已对这一问题做过讨论,这里给出一种更为简洁的证明方法.

命题2Santilli第二方法中求解函数B的计算式(14)式可以简化为

即有如下恒等式成立:

式中Rµ由(13)式给出.

证明将(13)式代入(14)式,具体运算得

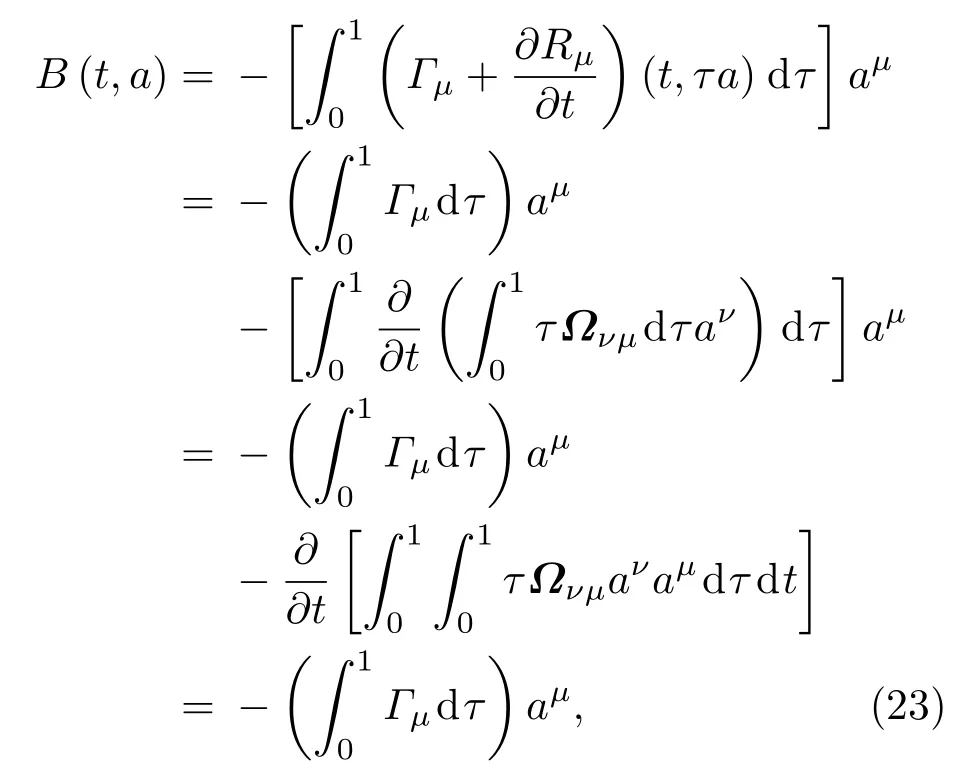
式中最后一个等号成立主要是因为Birkhoff张量Ωµν具有反对称性,因而第三个等号后的第二项中(Ωνµaνaµ)关于µ和ν的遍历求和恒为零,从而有

命题得证.

4.3 Santilli第三方法的改进及其MATLAB程序化计算

4.3.1 Santilli第三方法的性质及其第二形式

Santilli第三方法适用于可以求得全部独立第一积分的系统.此类系统的Birkhoff动力学函数B和Rµ都表示为这些积分的函数,因此借助第一积分这个桥梁可以找到B和Rµ之间的等量关系.

命题3由Santilli第三方法((15)式)所构造的Birkhoff动力学函数B和Rµ,总满足如下等量关系式[8]:

证明由于Iα(α=1,2,···,n)是系统的第一积分,故有

两端同乘以满足正规性条件((16)式)的函数Gα(t,a)得

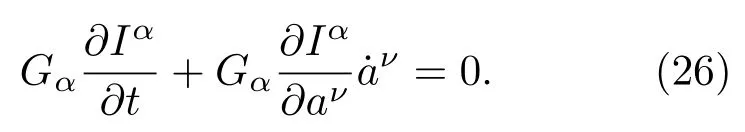
将(15)式代入(26)式即得(24)式.

利用这一关系可以将Santilli第三方法改写为如下新形式:

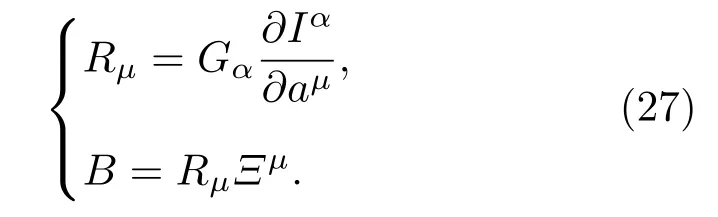
4.3.2 改进的Santilli第三方法

考虑Santilli第三方法的一种特殊形式.用Santilli第三方法((15)式)计算函数B和Rµ时,为保证得到的Birkhoff方程是正规的,要求(15)式中的函数Gα(α=1,2,···,2n)必须满足如下正规性条件:

但若对所选的每组Gα都去验证条件(28)式是否成立,将会导致额外的计算负担.于是提出如下问题:能否将可选函数Gα固定为某一组特殊的函数形式,使得正规性条件(28)式自动满足？事实上这是可以做到的,具体以如下命题形式阐述.

命题4假设给定系统的全部独立第一 积 分Iα(α=1,2,···,2n)已 知, 在 原Santilli第三方法((15)式)中按如下方式选取函数Gα(α=1,2,···,2n),即

或等价表示为

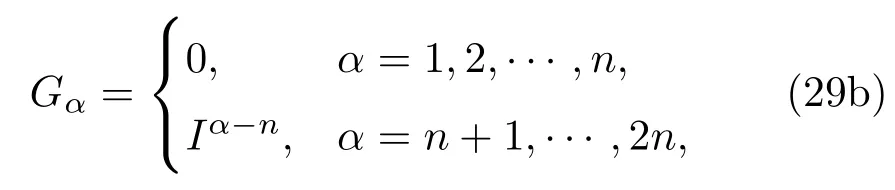
则正规性条件(28)式自动成立,并且函数B和Rµ可表示为

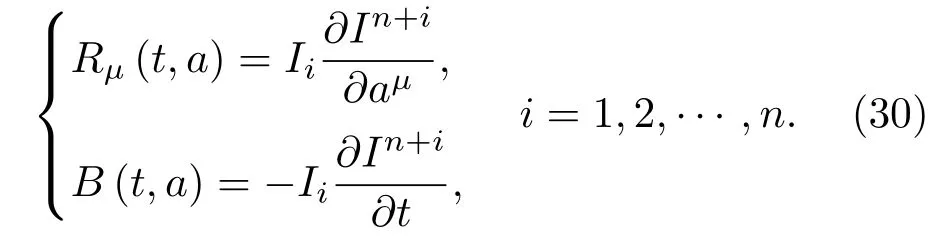
证明容易验证按照(29)式选取函数Gα(α=1,2,···,2n)后, 行列式((28)式)具体写为

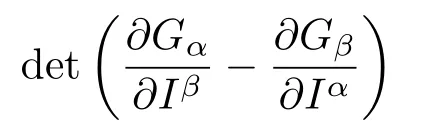
由行列式的结果不为零可知,正规性条件(28)式恒成立,再将函数Gα(α=1,2,···,2n)代入(15)式,即得函数B和Rµ的表达式((30)式).证毕.

构造方法(30)式称为改进的Santilli第三方法.显然,当应用改进的Santilli第三方法构造系统的Birkhoff动力学函数B和Rµ时,不必再进行检验正规性条件是否成立的步骤,在计算上显然是方便的,示例如下.

例1用改进的Santilli第三方法((30)式)构造Whittaker方程

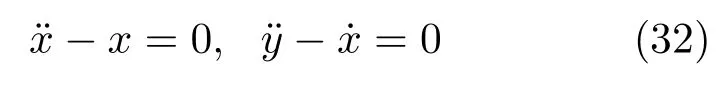
的Birkhoff动力学函数B和Rµ.

令

则系统((32)式)可表示为如下一阶标准形式:

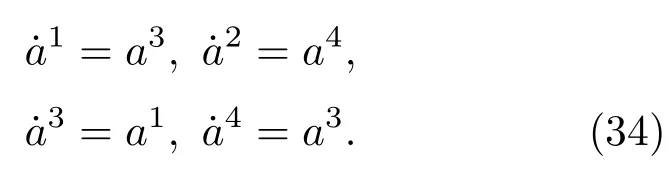
可求得系统全部独立的第一积分为

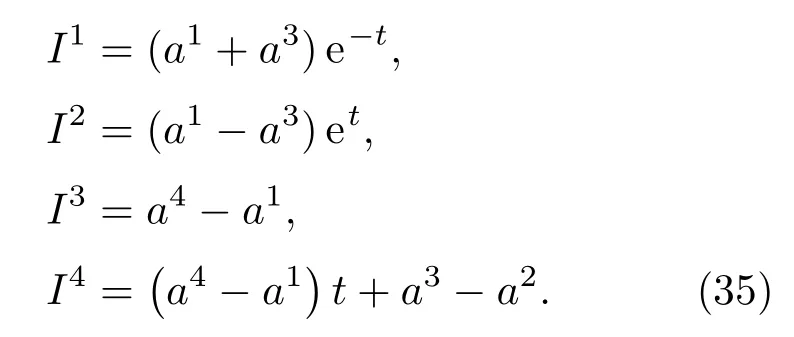
将(35)式代入(30)式得

具体计算得Birkhoff函数组Rµ为

Birkhoff函数B为

容易验证(37)式和(38)式是所需的B和Rµ,而且与用原Santiili第三方法算得的结果一致[9].

4.3.3 Santilli第三方法的MATLAB程序化计算

应用Santilli第三方法进行具体计算时,对于变量较多的系统必然会遇到以下问题:

2)若选取另外一组Gα,则要重复上述计算;

3)当验证B和Rµ是否满足Birkhoff方程((4)式)和关系式((24)式)时计算量大.

解决上述问题的有效途径自然是将计算过程程序化,这将带来如下便利:

1)消除计算量大带来的耗时、易出错、验证困难等问题;

2)可选取多组不同的Gα得到多组不同的B和Rµ,从中选出相对简单或具有物理意义的一组,这比利用规范变换简化B和Rµ容易得多.

为具体讨论Santilli第三方法的MATLAB程序化计算,首先绘制计算流程图,如图1所示.

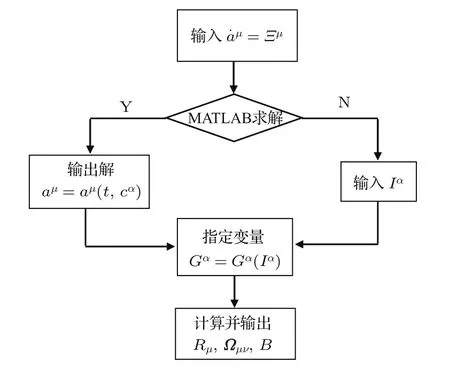
图1 Santilli第三方法MATLAB计算流程图Fig.1.Flow diagram of MATLAB program of the Santilli’s third method.

A)计算流程图

B)Santilli第三方法的矩阵形式及程序语句

下面根据流程图考虑程序化的具体实现.首先,将Santilli第三方法转换成MATLAB易于处理的矩阵形式;其次,将涉及到偏导数运算的各项用求Jacobi矩阵的方法代替,进而得到(12)式和Birkhoff张量Ωµν的MATLAB符号表示(详见表1),据此可以编写出具体的程序命令,并组合成完整的M文件;最后,在C)部分给出应用实例.

C)应用实例

例2已知如下约束力学系统:

令

则系统((39)式)的一阶标准形式为

试用MATLAB构造系统的Birkhoff表示.

首先,计算函数B和Rµ.利用B)部分的程序模板,在M文件中编写相应的语句,运行后返回系统的第一积分为

Birkhoff函数B和Rµ计算结果如表2所示.

表1 (15)式的张量形式及其MATLAB符号表示Table 1.The tensor form of Eq.(15)and its MATLAB symbol.

表2 函数B和Rµ的MATLAB计算结果Table 2.The calculation results of B and Rµ of Birkhoff’s functions by MATLAB.

表2中第一组值是取G1=I2,G2=I5,G3=0,G4=0,G5=0得到的,第二组值是取G1=I2,G2=0,G3=I1,G4=I5,G5=0得到的.第一组结果比第二组结果更为简单,但第二组的Birkhoff函数B具有能量的意义.对应于第一组G值的Birkhoff张量Ωµν为

若选取其他不同的G值,则可以得到不同的B和Rµ以及Birkhoff张量Ωµν.由本例的求解可以看出,Santilli第三方法的程序化计算,有效提高了计算效率和准确率.

5 结 论

作为Hamilton力学的推广,Birkhoff力学的发展一方面为完整非保守系统逆问题的研究提供了恰当的理论框架;另一方面也为Hamilton系统保结构计算的推广奠定了理论基础.开展Birkhoff动力学函数构造方法的研究,对于应用变分法理论、几何结构分析以及几何数值积分方法处理完整非保守系统的力学问题具有重要意义.

本文在命题1中证明了自治系统总有自治Birkhoff表示的结论,需要说明的是,这个自治Birkhoff表示并不一定是正规的.于是,自治系统是否总存在正规的自治Birkhoff表示,成为一个有待进一步研究的问题.命题2关于简化的Santilli第二方法的证明,比文献[17]中的方法简洁得多.研究这一问题的意义在于:简化的Santilli第二方法让我们认识到,通过求解Birkhoff动力学函数来确定Birkhoff方程,等同于确定它的辛矩阵.这种观点为研究Birkhoff动力学函数的构造方法提供了新视角.通过命题3所建立的函数B和Rµ之间的等量关系,定义了Santilli第三方法的新形式,再结合MATLAB程序化计算提高了Santilli第三方法的计算效率.

如何将物理学、力学、工程科学等领域中更多的动力学系统纳入Birkhoff系统？这是一个具有基本意义的研究课题,愿能引起更多研究者的关注.

[1]BirkhoffG D 1927Dynamical Systems(New York:AMS College Publishers Providence,RI,Vol.IX)

[2]Santilli R M 1978Foundations of Theoretical Mechanics I(New York:Springer-Verlag)pp219–235

[3]Mei F X 2009Inverse Problems of Dynamics(Beijing:National Defense Industry Press)pp261–263(in Chinese)[梅凤翔 2009动力学逆问题 (北京:国防工业出版社)第261—263页]

[4]Douglas J 1941Trans.Amer.Math.Soc.50 71

[5]Havas P 1957Nuovo Cimento Suppl.Ser.X5 363

[6]Marsden J E,Ratiu T S 1999Introduction to Mechanics and Symmetry.2nd Edition.(New York:Springer-Verlag)pp181–210

[7]Sarlet W 1982J.Phys.A15 1503

[8]Santilli R M 1983Foundations of Theoretical Mechanics II(New York:Springer-Verlag)pp25–28

[9]Mei F X,Shi R C,Zhang Y F,Wu H B 1996Dynamics of BirkhoffSystem(Beijing:Beijing Institute of Technology Press)pp8–25(in Chinese)[梅凤翔,史荣昌,张永发,吴恵彬1996 Birkhoff系统动力学(北京:北京理工大学出版社)第8—25页]

[10]Mei F X,Wu H B,Li Y M,Chen X W 2016Chin.J.Theor.Appl.Mech.48 263(in Chinese)[梅凤翔,吴惠彬,李彦敏,陈向炜2016力学学报48 263]

[11]Wu H B,Mei F X 2011Chin.Phys.B20 290

[12]Luo S K,He J M,Xu Y L 2016Int.J.Non-Linear Mech.78 105

[13]Luo S K,Dai Y,Zhang X T,Yang M J 2017Int.J.Non-Linear Mech.97 107

[14]Chen X W,Zhang Y,Mei F X 2017Chin.J.Theor.Appl.Mech.49 149(in Chinese)[陈向炜,张晔,梅凤翔2017力学学报49 149]

[15]Fu J L,Fu L P,Chen B Y,Sun Y 2016Phys.Lett.A380 15

[16]Kong X L,Wu H B 2017Acta.Phys.Sin.66 084501(in Chinese)[孔新雷,吴惠彬 2017物理学报 66 084501]

[17]Guo Y X,Liu C,Liu S X 2010Commun.Math.18 21

[18]Liu C,Song D,Liu S X,Guo Y X 2013Sci.Chin.Tech.Sci.43 541(in Chinese)[刘畅,宋端,刘世兴,郭永新2013中国科学:物理学力学天文学43 541]

[19]Feng K,Qin M Z 2003Symplectic Geometric Algorithms for Hamiltonian Systems(Hangzhou:Zhejiang Science&Technology Press)pp246–258(in Chinese)[冯康,秦孟兆 2003哈密尔顿系统的辛几何算法(杭州:浙江科学技术出版社)第246—258页]

[20]Zhang X W,Wu J K,Zhu H P,Huang K F 2002Appl.Math.Mech.9 915(in Chinese)[张兴武,武际可,朱海平,黄克服2002应用数学和力学9 915]

[21]Sun Y J,Shang Z J 2005Phys.Lett.A336 358

[22]Liu S X,Liu C,Guo Y X 2011Chin.Phys.B20 034501

[23]Ding G T 2008Acta.Phys.Sin.57 7415(in Chinese)[丁光涛 2008物理学报57 7415]

[24]Cui J C,Liao C C,Zhao Z 2016Acta.Phys.Sin.65 180201(in Chinese)[崔金超,廖翠萃,赵喆,刘世兴 2016物理学报65 180201]

[25]Cui J C,Song D,Guo Y X 2012Acta.Phys.Sin.61 244501(in Chinese)[崔金超,宋端,郭永新2012物理学报61 244501]

[26]Song D,Liu C,Guo Y X 2013Appl.Math.Mech.34 995(in Chinese)[宋端,刘畅,郭永新 2013应用数学和力学34 995]