亚大气压六相交流电弧放电等离子体射流特性数值模拟∗

郭恒 张晓宁 聂秋月 李和平 曾实 李志辉

1)(清华大学工程物理系,北京 100084)

2)(哈尔滨工业大学空间基础科学研究中心,哈尔滨 150001)

3)(哈尔滨工业大学电气工程及自动化学院,哈尔滨 150001)

4)(中国空气动力研究与发展中心超高速所,绵阳 621000)

5)(国家计算流体力学实验室,北京 100191)

(2017年11月29日收到;2018年1月4日收到修改稿)

1 引 言

在距离海平面20—100 km的空间区域,由于稀薄的大气环境有效地减小了飞行器在飞行过程中所受的空气阻力,从而较易实现高超声速飞行,成为人类航空与航天活动的重要区域之一,具有广阔的商业和军事应用价值,日益受到各国研究者的广泛关注.临近空间飞行器在高超声速飞行以及飞行器再入大气过程中,其表面激波热致产生高密度、强碰撞、非均匀以及热力学和化学非平衡态等离子体[1,2],从而使得飞行器面临着复杂的介质环境.这一方面表现为能量的注入和等离子体的存在所导致的飞行器周围局部区域当地声速增加、边界层特性的显著变化以及由此所引起的飞行器飞行阻力的变化[3];另一方面则表现为包覆于飞行器表面的等离子体鞘套环境对外来电磁波的吸收、散射和折射,引发“黑障”效应[4−6],进而影响飞行器的通信和控制系统.因此,开展高超声速飞行器与其周围复杂介质环境间相互作用机制的理论和实验研究对于指导飞行器的设计具有重要的意义.

从该领域目前的研究方法来看,主要包括了飞行实验、地面风洞实验和数值模拟.其中飞行实验[7−11]和地面风洞实验[12−14]尽管运行成本昂贵,且所能获得的实验数据有限,但却为科学研究积累了宝贵的实验数据.相比而言,采用螺旋波等离子体源、电弧等离子体源、辉光放电、电感/电容耦合放电等离子体源等[15−17]在地面开展小规模的实验室模拟以及借助于高性能电子计算机开展数值模拟研究,则是相对经济高效的科学研究方法.这样的研究方法尽管无法完全再现临近空间飞行器所面临的复杂介质环境,但从模拟飞行器与其周围复杂介质环境在某些方面的相互作用过程,如“黑障”问题中等离子体-波相互作用过程的研究以及高超声速飞行器在飞行过程中所面临的气动力和气动热环境来讲依然是十分有意义的.

以研究临近空间高超声速飞行器以及航天器再入大气环境飞行过程中“黑障”问题为背景,一方面,需要在地面模拟实验中产生具有足够大体积(如有效实验区长度L3=30—50 cm)、足够厚(如鞘套厚度δ=5—10 cm)以及足够高的等离子体密度(如电子数密度ne=108—1012cm−3)的包覆飞行器表面的等离子体鞘套环境(如图1所示),进而能够研究等离子体鞘套特性及其与入射电磁波间的相互作用规律;另一方面,飞行器飞行过程中所面临的高超声速流动环境将与飞行器壁面附近所产生的等离子体强烈耦合,从而呈现出气动力、气动热与非平衡态等离子体间复杂的耦合效应.在文献[15]中,作者着重讨论了将双射流直流电弧放电等离子体发生器的设计理念[16]与多相交流电弧放电等离子体发生器的设计理念[17,18]相结合,所建立的能够在大气压和亚大气压条件下放电产生大体积等离子体射流的六相交流电弧放电等离子体实验平台(multiphase gas discharge plasma experimental platform-2015,MPX-2015),并给出了不同放电参数(包括相邻电极之间的放电间距、弧电流、等离子体工作气体流量、真空腔压强以及水冷约束管直径等参数)下等离子体射流区气体温度、电子温度、电子数密度以及射流长度和直径等参数的变化规律.本文以MPX-2015为研究对象,着重采用数值模拟的手段研究非平衡态等离子体的特性.

图1 包覆飞行器的等离子体鞘套示意图Fig.1.Schematic of the plasma layer surrounding an aerocraft.

开展临近空间高超声速飞行器与其周围复杂介质环境间传热、流动以及电磁相互作用的研究,需要建立起一套能够自洽描述包覆飞行器表面的、具有可压缩、非平衡、热-电-磁-流动-化学反应强耦合特性的等离子体环境的物理数学模型,包括基本控制方程、输运系数和定解条件以及高效率的数值求解方法.在过去的几十年间,一方面,以计算流体力学模型为基础,国内外众多研究者针对高超声速飞行器飞行过程中的流动特性、热力学-化学非平衡特性开展了大量的研究工作,极大地推动了高超声速计算流体力学的发展[19−23];另一方面,在气动力/热与作为物质第四态的等离子体间复杂相互作用的研究中,尽管已经开展了不少有关描述非平衡态等离子体输运特性的物理数学模型(主要包括基本控制方程和输运系数)的研究(如文献[24—29]),但目前不同研究者所采用的物理数学模型依然不尽相同,特别是在基本控制方程与等离子体输运系数的定义和计算方法方面有时还不完全自洽,这在很大程度上影响了数值模拟所预测的临近空间飞行器飞行特性的准确性.因此,需要针对非平衡态等离子体中复杂的物理化学过程,建立和完善自洽描述非平衡态等离子体与环境气体间质量、动量和能量协同输运特性的物理数学模型,包括基本控制方程、初边值条件和输运性质参数数据库等.本研究组在前期的研究中应用渐进扰动的方法求解Boltzmann方程得到了描述粒子输运特性的守恒方程,进一步通过粒子间的相互作用计算得到了守恒方程中的输运系数[30,31],从而保证了等离子体中组分输运方程与其输运系数的自洽性,建立了自洽描述非平衡态等离子体输运过程的物理数学模型和以氩等离子体为模式体系的非平衡态等离子体输运系数的数据库[32].本文在此基础上针对MPX-2015实验系统开展非平衡态氩等离子体射流特性及其与环境冷气体和下游钝体间相互作用特性的数值模拟研究.其中,MPX-2015实验系统的6个电极均匀布置在同一圆周上,等离子体工作气体除了沿6个电极表面注入外,还可从电极平面上方注入;放电过程中,相邻两个电极间所加交流电压的相位差为60°;每相电流的波形均为标准正弦波,当其中1相的电流过零时,其他5相的电流并不会同时经过零点,从而保证了电弧的持续和一定程度上的稳定;每相的电流在70—110 A的范围内变化,两相之间的工作电压则维持在24 V左右;气体放电所产生的等离子体经过水冷约束管后进入真空腔.实验过程中可以采用发射光谱法测量等离子体射流区的气体温度、电子温度和电子数密度等参数.有关实验平台的具体描述可参见文献[15].本文第2部分讨论非平衡态等离子体特性数值模拟研究的物理数学模型;第3部分给出亚音速条件下自由射流特性计算结果以及与MPX-2015平台实验测量数据的对比,从而在一定程度上验证模型的正确性;第4部分给出从亚音速到超音速的非平衡态等离子体射流冲击钝体的数值模拟结果;第5部分给出本论文研究得到的主要结论,简要讨论后续研究需要解决的主要问题.

2 物理数学模型

2.1 基本控制方程

针对亚大气压条件下的非平衡态氩等离子体开展数值模拟研究,所采用的基本假定包括[30,31,33]:1)作为初步的研究工作,仅就六相交流放电等离子体射流的准稳态特性开展数值模拟研究,相应的实验对比亦采用时间平均的测量结果;2)尽管由于在物理上电子质量远远小于重粒子质量,从而导致电子与重粒子间弹性碰撞的能量交换效率极低,但由于整个等离子体体系中化学反应过程(如激发、电离及其相应的逆过程等)的存在,电子子体系和重粒子子体系并非两个孤立的子系统,而是相互间存在质量、动量和能量的交换过程;3)等离子体中粒子的自弛豫时间远小于能量交换的弛豫时间,于是,等离子体中电子和重粒子两个子体系的速度分布函数分别满足Maxwell分布,可分别定义电子温度(Te)和重粒子温度(Th);4)粒子间动量交换的弛豫时间远小于能量交换的弛豫时间,于是,宏观上可以将等离子体看作一种流体,流体速度为体系中所有粒子的质量平均速度;5)粒子的自弛豫时间远小于体系化学反应的弛豫时间,即等离子体的输运性质参数将不受化学反应的影响;6)i等离子体为光学薄,即等离子体对辐射能的吸收与全波长范围内的辐射能相比可忽略不计;7)等离子体工作气体及环境气体均为氩气,且处于层流流动状态;8)由于等离子体发生器水冷约束管的型线结构以及发生器进气口处的压强和真空腔内的环境压强均可调,从而使得等离子体射流可处于亚音速或超音速流动状态;9)不考虑钝体表面材料的烧蚀对其附近等离子体射流性质,特别是辐射特性的影响.

基于上述基本假定,在二维圆柱坐标系(z,r)下需要求解的基本控制方程包括连续性方程、组分质量平均的动量守恒方程以及重粒子与电子能量守恒方程,即:

在上述方程中,p,v,vr,vz,Th,Te,θ,jr,jz,Bθ,E,φ分别为等离子体的压力、速度矢量和其在径向、轴向的分量、重粒子温度、电子温度、电子温度与重粒子温度比(即Te/Th)、电流密度在径向和轴向的分量、自感应磁场的切向分量、电场强度矢量和电位;分别为氩等离子体的质量密度、黏性系数、重粒子平动热导率和非平衡热导率、电子平动热导率和非平衡热导率以及电导率.在局域化学平衡条件下,上述等离子体输运性质参数均为电子温度、重粒子温度以及压力的函数,可根据文献[30,31]中的定义与求解方法计算得到;na,ni,ne分别为原子、离子和电子数密度;τh:∇v为黏性耗散项;Urad和分别为等离子体单位体积的辐射热损失和电子-重粒子间弹性碰撞能量交换项;分别表示电子-原子以及电子-离子间的动量传输碰撞频率;me和mh分别为电子和重粒子的质量.由于在本文的数值模拟中仅对等离子体射流区特性进行计算,因此无需求解电磁场,即电位方程(7)无需求解;相应地,方程(2)—(5)中与电磁场有关的源项亦均忽略.

2.2 氩等离子体输运性质参数

开展非平衡态等离子体特性数值模拟的另一前提条件是与上述2.1节基本控制方程自洽的等离子体输运性质参数数据库的建立.数值模拟采用氩气为等离子体工作气体,基于文献[30,34]的方法开发了非平衡态氩等离子体组分、黏性系数、电子和重粒子平动热导率、组分扩散系数等输运性质参数计算的程序代码.在局域化学平衡条件下,上述等离子体输运性质参数均为电子温度、重粒子温度以及压力的函数,通过与求解2.1节偏微分方程组[方程(1)—(5)]的计算程序进行耦合迭代求解,最终获得不同工况下非平衡态氩等离子体射流特性的计算结果.

图2 氩等离子体重粒子平动热导率(λh,实线)、电子平动热导率(λe,虚线)和黏性系数(µ,点线)随电子温度和环境压强的变化规律(θ=2)Fig.2.Variations of the translational thermal conductivity of heavy particles(λh,solid line)and that of electrons(λe,dashed line),and viscosity(µ,dotted line)with the electron temperature and pressure(θ=2).

图2给出了环境压强p=100,1000和10000 Pa,电子与重粒子温度比θ=2的条件下氩等离子体黏性系数(µ)、电子平动热导率(λe)和重粒子平动热导率(λh)随电子温度(Te)的变化规律.为了便于比较,图2中上述3个输运系数均进行了归一化处理,归一化处理的参考值分别为10000 Pa下的µmax(0.0015 Pa·s@9200 K),λe(8.1600 W/(m·K)@30000 K)和λh(0.0114 W/(m·K)@9000 K). 从图2可以看到,在环境压强(p)和温度比(θ)一定的条件下,随着电子温度的升高,1)电子数密度和热运动速度均增大,从而导致电子平动热导率的单调增大;2)黏性系数和重粒子平动热导率的变化则相对比较复杂,在300—8000 K的温度区间内,随着电子温度的升高,二者单调增大,之后随着气体电离反应的增强,带电粒子间的长程的库仑作用势越来越重要,二者迅速降低,在15000 K后其值变得很小,并基本保持不变[32].在电子温度(Te)及温度比(θ)保持不变的情况下,环境压强(p)亦对等离子体的输运性质参数有着显著的影响,随着压力从100 Pa增加到10000 Pa,等离子体的黏性系数、电子和重粒子平动热导率均增大.此处需要说明的是,限于篇幅,本小节仅给出了非常有限的参数条件下的氩等离子体黏性系数以及电子和重粒子平动热导率随电子温度的变化曲线,而事实上,数值模拟需要广阔温度范围和压力范围内完备的等离子体输运性质参数.有关非平衡态等离子体输运性质参数的理论推导和计算方法可参见文献[34].

3 亚音速氩等离子体自由射流非平衡特性

3.1 计算域和边界条件的确定

为了验证本文数值模拟所建立的物理数学模型的正确性,首先在亚音速条件下对氩等离子体自由射流的非平衡特性进行了二维数值模拟研究,并与文献[15]中所得到的相同工况下的实验测量结果进行了对比分析.本节数值模拟采用第2节所给出的基本控制方程和输运性质参数,不同之处仅是由于较低的流速,忽略了重粒子能量方程中与可压缩效应相关的项,即方程(4)中的τh:∇v项.氩等离子体自由射流数值模拟所采用的计算域如图3所示,相应的边界条件列于表1.需要说明的是:本节数值模拟以文献[15]3.1节中典型的等离子体工作参数下(氩气总流量Qtot=16.0 slpm(standard liter per minute),其中从每个电极环缝注入的气体流量为Qe=1.0 slpm,电极平面上游的冷气体注入量为Qc=10.0 slpm;单相弧电流峰值I=80 A,相邻两电极间距le=40 cm,水冷约束管出口内径r1=2.5 cm,真空腔压强p=1000 Pa)测量得到的水冷约束管出口轴线上时间平均的等离子体电子温度(8000 K)和重粒子温度(4000 K)作为射流入口的温度边界条件,而速度边界条件则在保证总工作气体质量流量(对应于标准状况下的体积流量为Qtot=6×Qe+Qc=16.0 slpm)守恒的条件下折算得到入口处的速度边界条件,即vz=ρs·Qtot/(ρin·Sin)≈180 m/s,其中ρs和ρin分别代表标准状况下的气体密度和入口温度条件下的等离子体密度,Sin为水冷约束管喷嘴出口截面积.

图3 亚音速自由射流数值模拟计算域示意图Fig.3.Schematic of the calculation domain for the modeling of subsonic free plasma jet.

表1 亚音速自由射流数值模拟用边界条件Table 1.Boundary conditions used for the modeling of subsonic free plasma jet.

3.2 数值模拟结果与实验测量结果的对比分析

图4给出了Qe=1.0 slpm,Qc=10.0 slpm,I=80 A,le=40 mm,r1=2.5 cm,p=1000 Pa的典型工况下二维数值模拟得到的等离子体射流区气体温度分布与等离子体射流实验图像的对比.可以看到,数值模拟所得到的等离子体射流区重粒子温度的分布与实验拍摄到的射流强度定性一致.另外,计算得到的以电子数密度ne=1010cm−3的等值线度量的等离子体射流直径和长度分别为5.0 cm和65.0 cm;而实验测量得到的等离子体射流直径和长度则分别为5.5 cm和60.0 cm,二者亦符合较好.

图4 计算得到的等离子体射流区气体温度分布与实验照片的比较Fig.4.Comparison between the calculated gas temperature distribution and the discharge image.

图5则比较了相同工况下计算和实验得到的沿发生器几何轴线等离子体射流区重粒子温度(Th)、电子温度(Te)、电子数密度(ne)以及电子-中性粒子碰撞频率的变化规律.可以看到:1)上述四个参数的数值模拟结果与实验测量结果在定性的变化趋势上是完全一致的;2)由实验测量得到的在z=50.0 cm处的电子温度和重粒子温度均较数值模拟结果分别低22%和26%,而实验测得的电子数密度则与计算结果相差约18%,计算得到的电子-中性粒子碰撞频率则与实验值相差10%.但从总体上来看,本节二维非平衡数值模拟结果与实验测量结果较好地定性符合,这在一定程度上验证了本文所建立的物理数学模型用于亚音速流动条件下等离子体特性模拟的正确性.在此基础上,考虑可压缩性的影响,在第4部分开展跨音速和超音速流动条件下等离子体射流特性的数值模拟,这将为我们进行超音速等离子体射流特性的实验研究提供理论上的指导,而有关数值模拟和实验测量结果的对比分析,则还需要后续开展进一步的实验测量.

图5 计算得到的射流区等离子体参数沿其几何轴线的变化规律及其与实验测量结果的比较Fig.5.Comparisons of the calculated and measured plasma parameters along the jet axis.

4 超音速氩等离子体冲击射流非平衡特性

4.1 计算域和边界条件的确定

为了更加真实地模拟临近空间包覆高超声速飞行器的等离子体鞘套环境,不仅需要产生具有足够大尺寸和足够高电子数密度的等离子体,而且需要等离子体处于超音速流动状态下.在本节的研究中,针对MPX-2015实验系统首先从理论上对产生特定尺寸、超声速等离子体射流环境进行了数值模拟预测.为此,将文献[15]中约束电弧等离子体的水冷约束管内部型线从直筒型改为缩放喷管结构,通过对高温电弧等离子体流动的约束以及调整发生器进气口处与水冷约束管外真空腔边界的压差Δp实现等离子体流动从亚音速向超音速的跨声速流动.本节数值模拟所选取的计算域如图6所示,在放电区所产生的电弧等离子体经过缩放型喷管的入口(OA)后进行喷管内部,并从其出口(BH)流出后冲击其下游的钝体,进而在钝体表面(EFG)形成包覆钝体的等离子体鞘套.在本节数值模拟中,由于希望达到的最大马赫数为3.5左右,根据理想工作条件下喷管出口与喉部截面积之比与出口马赫数的关系[35],可以得到所采用的缩放型喷管的出口半径与其喉部半径之比应为2.0.等离子体发生器喷管下游钝体的尺寸根据RAM实际尺寸确定[36],其表面型线的表达式为

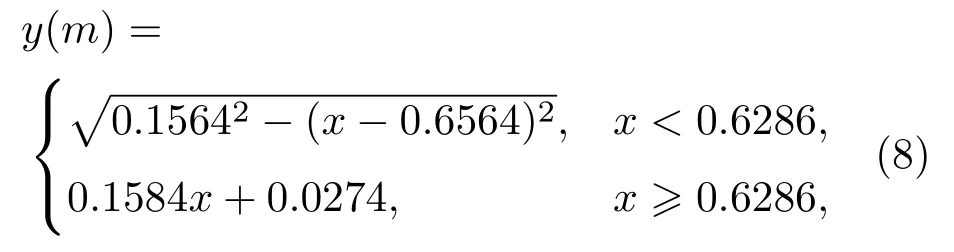
其中x和y分别代表距离坐标原点O的轴向距离和径向距离.图6中红色虚弧线代表了距钝体头部垂直距离为L的空间位置,而点K则为轴线上距离钝体头部5 cm处的位置.

本节数值模拟所采用的边界条件列于表2,其中边界CD和DE给定出口压力值,OA边界给定入口压力值,边界ABC和EFG则采用固壁边界条件.计算中参考压力面选在计算域入口处,即OA边界,并将压力值固定为5000 Pa,因此计算域的入口与出口之间的压力差为Δp,计算中通过改变Δp研究其对射流特性的影响.

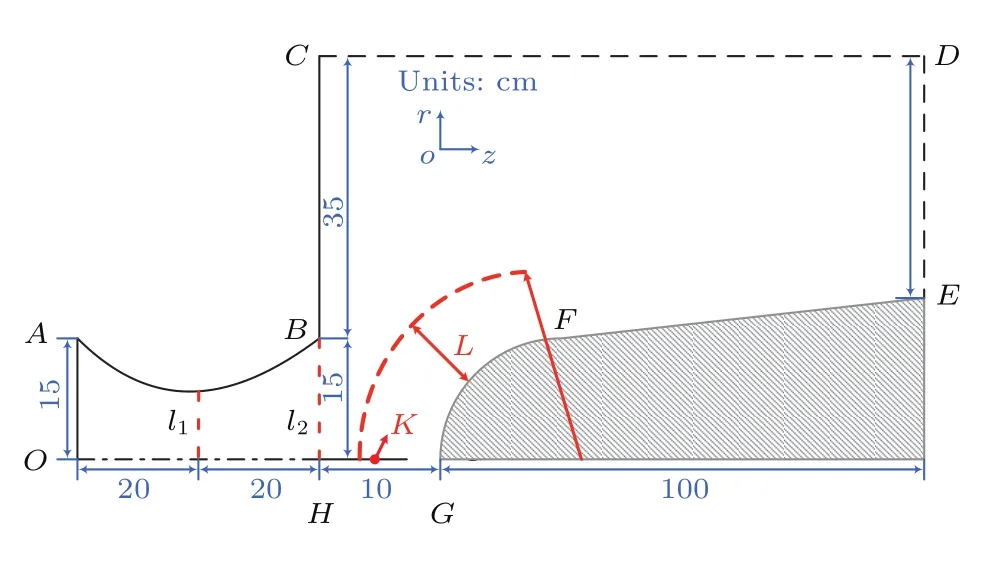
图6 等离子体冲击射流数值模拟计算域示意图Fig.6.Schematic of the calculation domain for the modeling of plasma impinging jet.

图7给出了缩放型喷管进出口压差Δp=900,2700,3500和4500 Pa条件下二维非平衡数值模拟计算得到的等离子体射流区马赫数(Ma)、电子数密度(ne),电子温度(Te)和重粒子温度(Th)的空间分布,图中的虚线表示距离钝体表面5 cm的空间位置.从图7可以看到:1)随着Δp的增大,等离子体流经缩放型喷管后逐步从亚音速流动发展成为超音速射流,喷管喉部下游最大马赫数从0.56增大到3.00;2)随着Δp的增大,包覆钝体的等离子体参数分布的空间均匀性显著降低,这一方面表现为钝体壁面附近高于临界电子数密度(ncrt=1010cm−3)的区域沿射流几何轴线明显缩小;而另一方面,Δp的增大亦使得在流动过程中射流区等离子体的内能与动能间随着空间位置不断发生转化,从而使得在钝体前缘附近随着动能向内能转化而导致电子数密度的显著增高(如图8所示),而在钝体后缘处则呈现出高电子密度区域收缩的变化规律.也就是说,随着喷管进出口压差的增大,钝体表面附近的电子数密度平均值增大,高电子数密度区域更加向钝体头部集中.

图7 不同Δp下等离子体射流区马赫数、电子数密度、电子温度和重粒子温度的等值线分布 (a)900 Pa;(b)2700 Pa;(c)3500 Pa;(d)4500 PaFig.7.Distributions of Mach number,electron number density,electron temperature and heavy-particle temperature in the plasma jet region with different values of Δp:(a)900 Pa;(b)2700 Pa;(c)3500 Pa;(d)4500 Pa.

表2 跨音速冲击射流数值模拟用边界条件Table 2.Boundary conditions used for the modeling of plasma impinging jet.

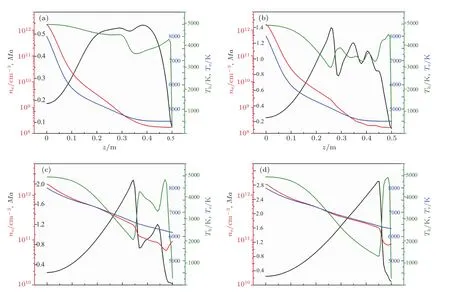
图8 不同Δp下钝体上游等离子体射流区马赫数、电子数密度、电子温度和重粒子温度沿轴线的变化规律 (a)900 Pa;(b)2700 Pa;(c)3500 Pa;(d)4500 PaFig.8.Axial profiles of Mach number,electron number density,electron temperature and heavy-particle temperature in the upstream of the bluff body with different values of Δp:(a)900 Pa;(b)2700 Pa;(c)3500 Pa;(d)4500 Pa.

图9给出了不同Δp下包覆钝体头部(FG)的等离子体区电子数密度高于临界电子数密度(ne,crt=1010cm−3)的最小鞘套厚度(δmin)以及钝体表面的总热流密度(Γtot)的变化规律.可以看到:1)随着Δp从300 Pa增大到2700 Pa,覆盖钝体头部的等离子体鞘套最小厚度从7.0 cm单调增加到15.0 cm,这与实验结果得到的趋势一致,而由等离子体注入钝体表面的总热流密度则变化较小,在5.0—6.0 kW之间波动;2)当Δp超过3000 Pa后,由于等离子体内能的损失,导致射流温度在喷管出口与钝体表面之间的区域相比于亚音速工况有所降低,因此δmin迅速降低到约3.0 cm,但是之后随着Δp的持续增加而缓慢增加到6.0 cm;而与此同时,Γtot则从5.5 kW单调降低到2.0 kW.

图9 不同Δp下钝体表面总热流密度和包覆钝体头部的等离子体鞘套最小厚度的变化规律Fig.9.Variations of the total heat flux to the bluffbody surface from plasmas and the minimum thickness of the plasma layer covering the head of the bluffbody under different values of Δp.

图10 不同Δp下钝体表面局部热流密度沿射流几何轴线的分布Fig.10.Profiles of the local heat flux to the bluffbody surface from plasmas along the geometrical axis of the plasma jet under different values of Δp.

图10则给出了不同喷嘴进出口压差条件下钝体表面热流密度沿射流几何轴线的分布规律.可以看到,在Δp保持不变的条件下,钝体头部(FG)区域的局部热流密度(Γ)较其后部区域(EF)要大得多,大约是后者的2—4倍;而且随着Δp的增加,沿钝体表面的热流密度分布变得愈加不均匀.由此我们可以得出这样的结论:在维持等离子体发生器进口气体压强不变的条件下,减小真空腔压强有利于提高等离子体射流的流动速度、降低等离子体射流向钝体表面的传热量,但覆盖钝体头部的等离子体鞘套的均匀性则显著降低,且其厚度呈现出先降低再升高的非单调性变化趋势.

5 结论与展望

本文以临近空间高超声速飞行器与其周围复杂介质环境间传热、流动以及电磁相互作用的研究为背景,进行了不同真空腔环境压强下等离子体自由射流和冲击射流的二维非平衡数值模拟,得到的主要结论包括:

1)在亚音速流动条件下,数值模拟结果与MPX-2015实验平台上的实验测量结果符合良好,这在一定程度上验证了本文数值模拟所建立的物理数学模型的正确性;

2)理论上通过调节缩放喷管进出口压力差可以实现高温等离子体流动从亚音速向超音速的发展.随着喷管进出口压差的增大,流经喷管的等离子体流动状态从亚音速发展为超音速;覆盖钝体表面的等离子体鞘套的厚度先减小而后又增加,鞘套的空间均匀性显著降低;等离子体射流向钝体表面的总传热量随之降低,而钝体头部壁面附近的电子数密度平均值则增大,即包覆钝体的等离子体鞘套的高电子数密度区域更加向钝体头部集中.

尽管数值模拟表明我们所建立的数学物理模型能够自洽描述包覆飞行器表面的、具有可压缩、非平衡、热-电-磁-流动-化学反应强耦合特性的等离子体环境,但本文仅对准稳态氩等离子体射流区进行了初步的数值模拟,并未开展电弧区更加复杂的包括电磁效应的非平衡态等离子体特性的数值模拟研究;而放电区的计算结果无疑会对射流区特性产生重要的影响.我们将在今后的工作中进一步深入开展不同工作气体,特别是空气条件下的跨音速非平衡态等离子体电弧射流特性的数值模拟研究,并通过测量不同流动状态下等离子体射流的速度分布[37,38]来与数值模拟结果进行更加仔细的对比分析.

[1]Keidar M,Kim M,Boyd I D 2008J.Spacecr.Rockets45 445

[2]Morris R A,Bench P M,Golden K E,Sutton E A 199937th Aerospace Sciences Meeting and ExhibitReno,NV,USA,January 11–14,1999 AIAA-99-0630

[3]Evans J S,Schexnayder Jr C J,Huber P W 1973NASA TN D-7332

[4]Gillman E D,Foster J E,Blankson I M 2010NASA/TM-2010-216220

[5]Rybak J P,Churchill R J 1971IEEE Trans.Aerosp.Electron.Syst.7 879

[6]Mather D E,Pasqual J M,Sillence J P,Lewis P 2005AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies ConferenceCapua,Italy,May 16–20,2005 AIAA-2005-3443

[7]Akey N D 1971NASA Special Publication252 19

[8]Watillon P,Berthe P,Chavagnac C 2003AIAA/ICAS International Air and Space Symposium and Exposition:The Next 100 yearsDayton,OH,USA,July 14–17,2003 AIAA-2003-2913

[9]Shirouzu M,Yamamoto M,Shirouzu M,Yamamoto M 1996Space Plane and Hypersonic Systems and Technology ConferenceNorfolk,VA,USA,November 18–22,1996 AIAA-96-4524-CP

[10]Yanagihara M,Munenaga T 200424th International CongressoftheAeronauticalSciencesYokohama,Japan,August 29–September 3,2004 p2004-7

[11]Sakurai H,Kobayasi M,Yamazaki I,Shirouzu M,Yamamoto M 1997Acta Astronaut.40 105

[12]Auweter Kurtz M,Kurtz H L,Laure S 1996J.Propul.Power12 1053

[13]Zhao L,Liu X X,Su H S 2015J.Telemetry,Tracking and Command36 28(in Chinese)[赵良,刘秀祥,苏汉生2015遥测遥控36 28]

[14]Hermann T,Löhle S,Zander F,Fulge H,Fasoulas S 2016J.Thermophys.Heat Transf.30 673

[15]Guo H,Su Y B,Li H P,Zeng S,Nie Q Y,Li Z X,Li Z H 2018Acta Phys.Sin.67 045201(in Chinese)[郭恒,苏运波,李和平,曾实,聂秋月,李占贤,李志辉 2018物理学报67 045201]

[16]Wang Z,Wu G Q,Ge N,Li H P,Bao C Y 2010IEEE Trans.Plasma Sci.38 2906

[17]Yao Y,Hossain M M,Watanabe T,Matsuura T,Funabiki F,Yano T 2008Chem.Eng.J.139 390

[18]Watanabe T,Liu Y,Tanaka M 2014Plasma Chem.Plasma Process.34 443

[19]Savino R,Paterna D,Fumo M S,D’Elia M 2010Open Aero.Eng.J.3 76

[20]Scalabrin L C,Boyd I D 20069th AIAA/ASME Joint Thermophysics and Heat Transfer ConferenceSan Francisco,CA,USA,June 5–8,2006 AIAA-2006-3773

[21]Gnoffo P A,Gupta R N,Shinn J L 1989NASA-TP-2867

[22]Candler G V,MacCormack R W 1991J.Thermophys.Heat Transf.5 266

[23]Huang H,Qu Z H 1999Acta Aerodyn.Sin.17 462(in Chinese)[黄华,瞿章华1999空气动力学学报17 462]

[24]Sun S R,Wang H X 2015Acta Phys.Sin.64 143401(in Chinese)[孙素蓉,王海兴 2015物理学报 64 143401]

[25]Wang H X,Sun S R,Chen S Q 2012Acta Phys.Sin.61 195203(in Chinese)[王海兴,孙素蓉,陈士强2012物理学报61 195203]

[26]Wang H X,Sun W P,Sun S R,Murphy A B,Ju Y 2014Plasma Chem.Plasma Process.34 559

[27]Niu C,Chen Z,Rong M,Wang C,Wu Y,Yang F,Wang X,Pang Q 2016J.Phys.D:Appl.Phys.49 405204

[28]Wang C,Wu Y,Chen Z,Yang F,Feng Y,Rong M,Zhang H 2016Plasma Sci.Technol.18 732

[29]Rat V,Murphy A B,Aubreton J,Elchinger M F,Fauchais P 2008J.Phys.D:Appl.Phys.41 183001

[30]Zhang X N,Li H P,Murphy A B,Xia W D 2013Phys.Plasmas20 033508

[31]Li H P,Zhang X N,Xia W D 2013Phys.Plasmas20 033509

[32]Zhang X N,Li H P,Murphy A B,Xia W D 2015Plasma Sources Sci.Technol.24 035011

[33]Zhang X N,Li H P,Xia W D 2013High Voltage Engineering39 1640(in Chinese)[张晓宁,李和平,夏维东2013高电压技术39 1640]

[34]Zhang X N 2015Ph.D.Dissertation(Hefei:University of Science and Technology of China)(in Chinese)[张晓宁2015博士学位论文(合肥:中国科学技术大学)]

[35]Tong B G,Kong X Y,Deng G H 1990Aerodynamics(Beijing:Higher Education Press)p73(in Chinese)[童秉纲,孔祥言,邓国华1990气体动力学 (北京:高等教育出版社)第73页]

[36]Fang M,Li Z H,Li Z H,Tian Y 2017Acta Aerodyn.Sin.35 39(in Chinese)[方明,李志辉,李中华,田颖2017空气动力学学报35 39]

[37]Li G,Xu Y J,Mu K J,Nie C Q,Zhu J Q,Zhang Y,Li H M 2008Acta Phys.Sin.57 6444(in Chinese)[李钢,徐燕骥,穆克进,聂超群,朱俊强,张翼,李汉明 2008物理学报57 6444]

[38]Meng X,Pan W X,Wu C K 2004J.Eng.Thermophys.25 490(in Chinese)[孟显,潘文霞,吴承康2004工程热物理学报25 490]