基于布洛赫方程的多色信标回波光子数数值仿真

王功长 魏凯 李岩

1)(清华大学精密仪器系,北京 100084)

2)(中国科学院光电技术研究所,自适应光学重点实验室,成都 610209)

(2017年9月1日收到;2017年11月13日收到修改稿)

1 引 言

在天文目标观测中,地基大口径光学望远镜常采用自适应光学系统实时探测并补偿光波受大气湍流影响所造成的波前畸变,从而得到接近衍射极限的目标图像[1].自适应光学系统工作时,须用天空中的亮星作为信标来获取大气湍流造成的波前畸变信息.天文自适应光学系统早期采用恒星作为信标即自然信标,但是能达到自适应校正所需的亮度很少,并且一个信标只能对其等晕区的目标进行校正,这就使得天文自适应光学系统的天空覆盖率很低,即便在近红外波段成像,天空覆盖率仍不足1%[2].为了解决自然信标自适应光学系统天空覆盖率低的问题,人们提出了人造激光信标技术.产生人造信标的方法有两种:一种是利用激光激发大气中的气体分子,利用气体分子的后向瑞利散射产生人造信标,即瑞利信标[2];另一种是通过激光共振激发大气中间层约90 km高度分布的钠原子,利用钠原子的共振散射产生人造信标,即钠信标[3].而后为了获得更大的高分辨力成像视场,又发展了多颗信标构成信标阵列技术来进一步消除非等晕误差.

虽然人造信标的应用使得大型地基天文望远镜自适应光学系统的天空覆盖率有了很大的提高[4−6],但是不管是单颗人造信标还是多颗人造信标,都只能用来探测大气波前的高阶像差,而不能用来获得大气波前的倾斜像差[7].当今国际上采用人造信标的地基望远镜[8−11],一般是在利用激光信标校正高阶像差的同时,还必须寻找一颗较低亮度的自然导星来探测倾斜像差.虽然找到这样亮度的自然信标的概率大幅增加,K波段可达30%—60%[9,12],但仍不能实现真正意义上的100%天空覆盖率.

1995年,法国科学家Foy等[13]提出了采用多色信标进行倾斜信息探测的方法,即采用两束激光(589 nm,569 nm)级联激发中间钠层,使钠原子由基能级3S1/2能级激发至3P3/2能级,再由3P3/2能级激发至4D5/2能级,处于4D5/2能级的钠原子由于自发辐射会产生不同波段的光(330 nm,569 nm),不同波段的光经过大气时折射率的不同而产生不同的角度偏转,从而差分计算出大气湍流倾斜像差,如(1)式所示:

式中θ(λ)为λ波段大气湍流倾斜像差,n(λ)为λ波段大气折射率,Δn330,569为330 nm与569 nm大气折射率之差,Δθ330,569为330 nm与569 nm倾斜角度之差.

Foy等[14−19]对多色信标多个波段回光强度进行了探测,并根据回光强度分析多色信标进行倾斜探测是可行的[20,21].2006年,Pique等[22,23]又提出了一级激发钠原子产生多色信标的方法,即采用一束激光(330 nm)直接将处于基能级3S1/2能级的钠原子激发至4P3/2能级,处于4P3/2能级的钠原子由于自发辐射产生不同波段的光,并提出该方法激发330 nm回波光子数要高于级联激发的回波光子数.目前多色信标发展的主要限制是现有的激光器功率条件下330 nm的回波光子数,仍然无法满足倾斜探测精度的需求[24],然而数十瓦、高光束质量的330 nm波段激光器研制难度大、费用高,如何在设计之初即明确激光器的最优参数,使得330 nm的回波光子数达到最大,是多色信标研究的一项重要内容,急需准确模拟激光与中间层钠原子相互作用产生多色信标的物理过程.

现阶段多色信标仿真模型都存在一定的不足.BEACON程序[25]采用求解布洛赫方程的方法,模拟仿真级联激发钠原子产生多色信标,但BEACON程序没有考虑中间层原子间以及原子与分子间的碰撞,也没有考虑原子吸收光子后的反冲作用,而碰撞与反冲又被认为在激光与原子相互作用时起着非常重要的作用[26−29].而且BEACON程序模拟受激吸收和自发辐射时,在受激吸收时无自发辐射产生,在自发辐射时又没有考虑受激吸收作用[24],所以BEACON程序只能仿真短脉冲激光器,而不能仿真长脉冲或者连续激光器.Pique等[23]采用速率方程建立一级激发钠原子形成多色信标仿真模型,但该模型采用的吸收截面被认为是不够准确[30,31]以及该模型对相位调制激光器的仿真与Morris[32]以及Bellanger等[25]基于布洛赫方程的仿真模型不一致[30,31],而无法准确计算出回波光子数.本文针对一级激发中间层钠原子产生多色信标的物理过程,提出了基于布洛赫方程的仿真模型,充分考虑中间层钠原子的多普勒展宽、钠原子间及钠原子与分子(O2,N2)间的碰撞、钠原子进出作用场以及钠原子吸收光子后反冲作用的影响,并对各波段回波光子数以及激光器参数对回波光子数的影响进行仿真分析.

2 物理过程

一级激发钠原子产生多色信标的能级结构图如图1所示,一束330 nm的激光将中间层钠原子由基能级3S1/2能级激发至4P3/2能级,处于4P3/2能级的钠原子向3S1/2能级和4S1/2能级自发辐射产生330 nm和2206 nm的光,处于4S1/2能级的钠原子向3P3/2能级和3P1/2能级自发辐射产生1140 nm和1138 nm的光,处于3P3/2能级的钠原子向3S1/2能级自发辐射产生589 nm的光,处于3P1/2能级的钠原子向3S1/2能级自发辐射产生589.6 nm的光,这时就可以采用自发辐射的330,589 nm回光经过大气时折射率的不同进行倾斜探测[23].图1中各能级自发辐射波长及寿命数据来源于Sansonetti的收集[33].4P3/2能级的钠原子自发辐射的过程中,本文只考虑向3S1/2和4S1/2能级的自发辐射,根据Sansonetti的收集[33]及NIST database[34]的数据,向3P1/2,3P3/2,3D3/2和3D5/2能级的自发辐射概率很小,故而本文予以忽略.

图1 一级激发钠原子产生多色信标的能级结构图Fig.1.Energy diagram of polychromatic laser guide stars with one-photon excitation of sodium.

在分析激光与钠原子作用的物理过程时,根据半经典理论,将激光看作经典的电磁波用麦克斯韦方程表示,将钠原子看作被量子化的系统用布洛赫方程表示,入射激光与钠原子的相互作用过程可通过求解光学布洛赫方程得出.但是真实的激光与中间层钠原子的作用过程除分析光与物质相互作用外,还需要考虑外部环境的影响,如中间层温度带来的多普勒展宽以及如图2所示原子进出激光束速率、碰撞、反冲等因素对整个作用过程的影响.

图2 激光与中间层钠原子作用需考虑的因素Fig.2.The factors should be considered of laser interaction with mesospheric sodium atoms.

3 方程的建立

为了计算一级激发钠原子多色信标的回光光子数,本文采用光学布洛赫方程来描述激光与钠原子作用时钠原子的状态演变,在方程的建立过程中充分考虑了多普勒展宽、原子进出激光束速率、碰撞、反冲等因素对钠原子状态演变的影响.

3.1 初始方程

描述激光与钠原子相互作用,首先从Liouville方程[35]来推导:

为密度矩阵,用来表示钠原子系综状态. 如图1所示,采用|1〉,|2〉,|3〉,|4〉,|5〉表 示 钠 原 子3S1/2,3P1/2,3P3/2,4S1/2,4P3/2能态. ħ =h/(2π),h为布朗克常量;H为总哈密顿量,本文中H可表示为H0+He;H0为原子内部电子-原子核库仑相互作用的哈密顿量;ω1,ω2,ω3,ω4,ω5为钠原子3S1/2,3P1/2,3P3/2,4S1/2,4P3/2能态本征能量对应的角频率.

He为激光场与钠原子相互作用的哈密顿量,He=d·E,其中d为电偶极子算符,E为激光场对应的电场强度.

ˆΓ为弛豫矩阵,弛豫矩阵是对角矩阵,对角线上元素为每个能级的衰减速率,对于自发辐射,

Γb,a为b能级向a能级自发辐射速率.

Λ为粒子数再生矩阵,密度矩阵中上能级ρrs因自发辐射对下能级ρmn产生的变化为[35]

功率密度为I、角频率为ωL、沿Z方向传播的激光激发钠原子时,光场振幅为光速,ε0为介电常数,频率偏移为ΔL=ωL−(ω5−ω1),将哈密顿量进行旋转波近似后,方程(2)可以写成:

〈1‖d‖5〉为能级1与能级5间电偶极子:

(8)式中J1,J5为钠原子3S1/2,4P3/2能级的角动量,方程组(7)为线性微分方程组,也被称作光学布洛赫方程组.

3.2 多普勒展宽

3.1节的分析是认为中间层钠原子是静止的或者在激光传输方向上是没有速度的,但是实际中中间层是有温度的,钠原子存在热运动,产生多普勒展宽,使得钠原子的分布随速度大小发生变化.

在激光传输方向钠原子的速度分布满足Maxwell-Boltzmann分布:

式中m为原子质量,kB为玻尔兹曼常数,T为温度,υ激光传输方向钠原子的速度.

因为原子存在速度就会产生多普勒频移,ΔD=−kυ,k为波数.这样多普勒频移的分布也服从Maxwell-Boltzmann分布:

钠原子3S1/2→4P3/2激发过程在温度为185 K的多普勒展宽如图3所示.为了便于计算多普勒展宽的影响,将钠原子按照速度分布划分为许多速度组,速度组越多,对多普勒展宽的影响计算越准确.对于特定的速度组i,如图3所示频率偏移范围为[a,b],则

Pi为钠原子处于速度组i的概率,ΔD,i为速度组i的多普勒频率频移.这时,激光与速度组i的钠原子作用时的整体频率偏移为

图3 钠原子3S1/2→ 4P3/2激发过程在温度为185 K时的多普勒展宽Fig.3.Doppler-broaden of sodium 3S1/2→4P3/2line for temperature of 185 K.

3.3 进出作用场

中间层钠原子存在着热运动以及风速等因素的影响,就会存在钠原子进出激光作用场如图2所示,造成粒子数再生发生变化.

设钠原子进出作用场的速率为γ进出,那么对于特定的速度组i,钠原子进出速度组i的速率为Piγ进出,则速度组i的弛豫矩阵及粒子数再生矩阵应为:

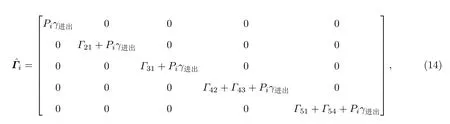
3.4 碰 撞

中间层钠原子与其他分子(N2,O2)的热运动,也使得钠原子之间以及钠原子与分子间存在不停地相互碰撞,产生能量和动量的交换,使得钠原子的速度发生改变.

假设钠原子与钠原子以及钠原子与分子碰撞后,钠原子的速度分布仍然服从Maxwell-Boltzmann分布与碰撞前钠原子的速度无关,假设碰撞发生的速率为γ碰撞,那么对特定的速度组i,因碰撞出该速度组的速率为γi=(1−Pi)γ碰撞,其他速度组因碰撞进入速度组i的速率为γ′i=Piγ碰撞,这时对速度组i,弛豫矩阵和粒子数再生的矩阵为

3.5 反 冲

当钠原子受激吸收光子时,能量增加hν,动量改变ħk,则速度在激光光束方向增加υr=ħk/m,即反冲作用.而自发辐射在各个方向都是均匀的,平均后自发辐射引起的速度改变为0.

对特定的速度组i,速度组范围Δυi(υr＜Δυi),吸收光子后的钠原子有υr/Δυi部分进入i+1组,吸收光子后的钠原子有1−υr/Δυi部分还在i速度组.此时速度组i的粒子数再生矩阵应写为

3.6 总方程

综合原始方程、多普勒展宽、进出作用场、碰撞、反冲的影响,根据方程(2),特定速度组i的布洛赫方程表达出来,如果是连续激光器作用时,平衡状态下则

又因为Λi包含常数项,则布洛赫方程组可以写成矩阵形式:

那么对于N个速度组的总方程应为

根据之前的分析,容易看出系数矩阵为满秩矩阵,则方程存在惟一解.则各波段的自发辐射的光子数应为

关于速度组的划分,本文采用Holzlöhner等[28]以及LGSBloch程序包[36]的划分方法,将整个频率区间划分为800个速度组.

关于激光器线宽的仿真,本文采用Holzlöhner等[28]和Kane等[37]提到的方法,即采用两束相位相差为π的激光同时激发原子模拟激光器线宽,并且两束激光束间的转换速率正比于激光器线宽.

另外,本文只计算了连续型激光器的激发过程,关于脉冲型激光器的仿真可以采用Holzlöhner等[38]提出的方法进行仿真,将未饱和脉冲型激光器仿真转换为连续型激光器的仿真,或者将脉冲形状离散化采用(21)式计算出整个脉冲持续时间内的回波光子数.

式中,Δt为离散化后某一激光器强度持续时间,A为该激光器强度下的系数矩阵,ρcw为该强度下连续型激光作用时的解.

因为脉冲型可以转化为连续型求解,或者将连续型解代入(21)式进行求解,本文先重点分析连续型激光器的作用过程.

4 仿真参数的选择

本文采用的一些基本物理常量以及钠原子质量来源于Steck[39]的整理和计算,钠层基本信息来源于Holzlöhner等[28]的分析,钠层的平均高度为92 km,中间层温度为185 K,钠层柱密度为4.0×1013m−2.

根据Holzlöhner等[28]的计算,进出作用场的速度与钠原子在中间层的扩散速度、中间层的风速、传输过程中的光束弯曲、望远镜的跟踪速度有关,而这几项中起主要作用的为钠原子在中间层的扩散速度,该速度与光斑大小成反比.进出作用场的速率为进出作用场的速度与光斑大小的比值,又光斑大小正比于激光波长,所以我们估计330 nm激光作用中间层钠原子时进出作用场的速率为589 nm激光作用中间层钠原子时进出作用场的速率的(589/330)2倍,文献[25]估计589 nm激光作用中间层钠原子时进出作用场的速率为1/(6 ms),则330 nm激光作用中间层钠原子时进出作用场的速率为1/(1.833 ms).

文献[26]提出中间层钠原子在Δt时间内与其他原子或者分子碰撞发生的概率为

式中

T为温度,ns为与钠原子发生碰撞的分子或原子的密度,σs为碰撞的散射截面,ms为碰撞分子或原子的质量,υ为钠原子的运动速度.

钠原子在中间层的速度分布满足Maxwell-Boltzmann分布为

由以上两式,并在钠原子的速度上积分,可以得出钠原子的平均碰撞速率为

由于缺少对大气中间层温度的变化以及缺少对中间层相关气体参数的测量,对于钠原子的碰撞速率目前只能粗略的估算.根据Holzlöhner等[28]提供的估算结果,在92 km处钠原子与气体分子的平均碰撞速率为1/(35µs),Milonni等[26]给出的估算则是1/(100µs).本文采用Holzlöhner的估算结果1/(35µs),对碰撞速率对回光效率的影响进行了分析.

当原子吸收光子时,能量增加hν,动量改变ħk,则速度增加υr=ħk/m,即反冲作用.对于激发钠原子4P3/2能级而言,速度增加υr=ħk/mNa=5.25 cm/s,则由反冲引起的多普勒频移为

即在钠原子3S1/2→4P3/2的激发过程中,钠原子吸收光子之后,因反冲作用的影响多普勒频移会增加159 kHz.

5 仿真结果分析

根据第3节给出的计算方法以及第4节的参数,利用Atomic Density Matrix仿真平台[40],编写了基于布洛赫方程的一级激发钠原子多色信标仿真程序,对回光效率进行了仿真,并对各个因素对回光效率的影响进行了分析.

5.1 回光效率

采用不同的功率密度进行回光效率的仿真计算,得到功率密度与各波段回光效率的曲线如图4所示.由图4可以看出:330 nm的回光效率最低,在功率密度为2 W/m2时,回光效率为0.87 Photons/[s·sr·atom·(W/m2)]; 而 2206 nm 的回光效率最高,在功率密度为2 W/m2时,回光效率为2.78 Photons/[s·sr·atom·(W/m2)]; 连续激光器作用时,达到平衡状态后进出3P3/2能级和3P1/2能级的粒子数相等,即图中589 nm回光效率与1140 nm回光效率基本相同,589.6 nm的回光效率与1138 nm的回光效率基本相同;而进出3S1/2能级的粒子数相等,则2206 nm的回光效率基本上为1138 nm与1140 nm的回光效率之和;各波段的回光效率与功率密度曲线的趋势基本一致,即在功率密度较低时(＜1 W/m2),回光效率变化不大,但是在功率密度大于2 W/m2时回光效率随着功率密度增加呈逐渐下降的趋势,这主要是饱和作用的影响.

图4 功率密度与回光效率曲线Fig.4.Curves of the power density and the return flux efficiency.

5.2 各能级的粒子数布居

分别采用功率密度为1,5,10,20 W/m2仿真不同频率偏移下各能级的粒子数布居,仿真结果如图5所示.在一定的功率密度范围内,各能级粒子数布居随着功率密度的增大而增大;在功率密度一定时,随着频率的偏移,各能级的粒子数布居逐渐降低,其分布基本与钠原子z方向上的速度分布基本相同;在相同的功率密度和频率偏移下,4P3/2能级粒子数布居最大,这是由一级激发钠原子产生多色信标的物理机制决定的,只有处于4P3/2能级的钠原子自发辐射后,除基极以外的低能级才能存在粒子数布居.

图5 3P1/2,3P3/2,4S1/2,4P3/2能级粒子数布居Fig.5.Population of 3P1/2,3P3/2,4S1/2,4P3/2levels of sodium.

5.3 各参数对回光效率的影响

以330 nm的回光效率为例分析进出作用场速率、碰撞、反冲等对回光效率的影响.

由图6(a)可以看出进出场速率为1/ms和1/10 ms量级时,对回光效率的影响不大,从图形中几乎看不出变化,但是当增大到1/(100µs)量级时,将会使回光效率曲线的整体趋势向右移动,即其饱和功率密度会增加.从图6(b)碰撞的图形上看,碰撞的速率越大,回光效率曲线向右平移的整体趋势越明显,如碰撞速率从1/(35µs)增大至1/µs时,回光效率曲线下降较明显的点由1 W/m2增大至约10 W/m2,这说明碰撞也会使饱和功率密度增大,并且速率越大增大得越多.图6(c)表明反冲会使回光效率的整体趋势左移,不考虑反冲时,回光效率曲线下降较明显的点由1 W/m2增大至约10 W/m2,即反冲作用会使得饱和功率密度减小.图6(d)为功率密度10 W/m2时考虑反冲作用和未考虑反冲作用的基能级粒子数速度分布,可以看出考虑反冲作用时的孔烧效应远大于未考虑反冲作用的孔烧效应,考虑反冲作用后,中心频率基能级粒子分布变为原来的44%,并且反冲作用还会引起基能级的粒子数在一定的范围内右移.增大激光器线宽会使考虑反冲作用后的孔烧效应形状变得扁平.

5.4 激光器线宽优化回光效率

图7所示为单模激光器不同线宽(洛伦兹线型)、不同功率密度时330 nm的回光效率,可以看出不同的功率密度存在一个最优的线宽,使得回光效率达到最高.如当功率密度为10 W/m2时,随着线宽的增加,回光效率也增加,当线宽增加到约18 MHz时,回光效率达到最大,约为0.907 Photons/[s·sr·atom·(W/m2)], 当继续增加线宽时, 回光效率将逐渐下降.随着功率密度的增大,使得回光效率最大的最佳线宽也逐渐增大,而最大回光效率的数值则逐渐降低.

图6 (a)进出作用场,(b)碰撞,(c)反冲对回光效率的影响以及(d)反冲作用对基能级粒子数分布的影响Fig.6.Effects of(a)beam atom exchange,(b)collision,(c)recoil on return flux efficiency and(d)effect of recoil on the population of ground-state.

图7 回光效率与功率密度、线宽等高线图Fig.7.Contour plot of Ψ(I,linewidth).

6 结 论

充分考虑中间层钠原子多普勒展宽、进出作用场速率、碰撞、反冲等因素,建立了基于布洛赫方程的激光一级激发钠原子产生多色信标的仿真模型,计算多色信标的回波光子数,并对描述回波光子数大小的回光效率进行了仿真计算,详细分析了进出作用场速率、碰撞、反冲等因素以及激光器线宽对回光效率的影响.得到以下结论:

1)一级激发钠原子产生多色信标时,330 nm的回光效率最低,而2206 nm的回光效率最高,589 nm回光效率与1140 nm回光效率基本相同,589.6 nm的回光效率与1138 nm的回光效率基本相同,并且随着激光器功率的增大,回光效率逐渐下降,这主要是饱和效应的影响;

2)进出作用场速率在小范围内变化对整个回光效率功率密度曲线几乎没有影响,碰撞速率的增大会导致整个回光效率功率密度曲线整体趋势向右平移,即饱和功率密度增大,而反冲会使得整个回光效率功率密度曲线整体趋势向左平移,即反冲作用会使饱和功率密度减小;

3)不同的功率密度都存在一个最优的激光器线宽,而并不是激光器线宽越大越好,当功率密度为10 W/m2时,最优线宽约为18 MHz.

本文在钠原子能级结构建模时暂没有考虑超精细结构以及塞曼分裂,还需进一步分析地磁场、碰撞引起的自旋交换等对整个作用过程的影响.

感谢中国科学院光电技术研究所晋凯博士以及黄建博士对本文的有益讨论.

[1]Babcock H W 1953Publ.Astron.Soc.Pac.65 229

[2]Hardy J W 1998Adaptive Optics for Astronomical Telescopes(New York:Oxford University Press)pp216–265

[3]Happer W,Macdonald G,Max C 1994J.Opt.Soc.Am.A11 263

[4]Thompson L A,Gardner C S 1987Nature328 229

[5]Greenwood D P,Primmerman C A 1992LLabJ5 3

[6]Fugate R Q,Spinhirne J M,Moroney J F,Cleis R A,Oliker M D,Boeke B R,Ellerbroek B L,Higgins C H,Ruane R E,Swindle D W,Jelonek M P,Lange W J,Slavin A C,Wild W J,Winker D M,Wynia J M 1994J.Opt.Soc.Am.A11 310

[7]Rigaut F,Gendron E 1992Astron.Astrophys.261 677

[8]Correia C M,Neichel B,Conan J M,Petit C,Sauvage J F,Fusco T,Vernet J D R,Thatte N 2016SPIE Astronomical Telescopes+InstrumentationEdinburgh,June 26–July 1,2016 p99094H

[9]Boyer C,Adkins S,Andersen D R,Atwood J,Byrnes P,Cavaco J,Ellerbroek B,Gilles L,Gregory J,Herriot G 2014SPIE Astronomical Telescopes+InstrumentationPalais des Congrès de Montréal,June 22–27,2014 p91480X

[10]Bouchez A H,Acton D S,Biasi R,Conan R,Espeland B,Esposito S,Filgueira J M,Gallieni D,Mcleod B A,Pinna E 2014SPIE Astronomical Telescopes+InstrumentationPalais des Congrès de Montréal,June 22–27,2014 p91480W

[11]Wizinowich P L,Le Mignant D,Bouchez A H,Campbell R D,Chin J C Y,Contos A R,van Dam M A,Hartman S K,Johansson E M,Lafon R E,Lewis H,Stomski P J,Summers D M 2006Publ.Astron.Soc.Pac.118 297

[12]Meilard N,Foy R,Langlois M,Tallon M,Thiébaut E,Petit A,Blazit A,Blanc P E,Chombart J,Fouche O 2010SPIE Astronomical Telescopes and Instrumentation,San Diego,June 27–July 2,2010 p77361W

[13]Foy R,Migus A,Biraben F,Grynberg G,Mccullough P R,Tallon M 1995A&AS111 569

[14]Friedman H,Foy R,Tallon M,Migus A 1996Office of Scientific&Technical Information Technical Reports

[15]Schoeck M,Foy R,Pique J P,Chevrou P,Ageorges N,Petit A D,Bellanger V,Fews H,Foy F C,Hoegemann C K 2000Proc.SPIE4007 296

[16]Froc G,Rosencher E,Attal-Trétout B,Michau V 2000Opt.Commun.178 405

[17]Foy R,Tallon M,Tallonbosc I,Thiébaut E,Vaillant J,Foy F,Robert D,Friedman H,Biraben F,Grynberg G 2000J.Opt.Soc.Am.A17 2236

[18]Foy R,Tallon M,Thiebaut E,Vaillant J,Pique J P,Mueller D,D’Orgeville C,Segonds P,Petit A D,Chevrou P 2000Proc.SPIE4007 284

[19]Schoeck M,Foy R,Pique J P,Tallon M,Laubscher M 1999Proc.SPIE3762 321

[20]Foy R,Pique J P,Bellanger V,Petit A D,Hogemann C K,Noethe L,Schock M,Tallon M,Thiebaut E,Vaillant J 2003Proc.SPIE4839 484

[21]Foy R,Pique J P,Petit A D,Michau V,Bellanger V,Deron R,Hoegemann C K,Laubscher M,D’Orgeville C,Schoeck M 2000Proc.SPIE4065 312

[22]Pique J P,Moldovan I C,Fesquet V,Chatellus H G D,Marc F 2006Proc.SPIE6272 62723D

[23]Pique J P,Moldovan I C,Fesquet V 2006J.Opt.Soc.Am.A23 2817

[24]Guillet D C H,Pique J P,Moldovan I C 2008J.Opt.Soc.Am.A25 400

[25]Bellanger V,Courcelle A,Petit A 2004Comput.Phys.Commun.162 143

[26]Milonni P W,Fearn H,Telle J M,Fugate R Q 1999J.Opt.Soc.Am.A16 2555

[27]Hillman P D,Drummond J D,Denman C A,Fugate R Q 2008Proc.SPIE7015 70150L

[28]Holzlöhner R,Rochester S M,Calia D B,Budker D,Higbie J M,Hackenberg W 2010Astron.Astrophys.510 1109

[29]Feng L,Jin K,Shen Z,Wei K 2015Applied Optics and PhotonBeijing,China,May 5–7,2015 p96781B

[30]Foy R,Fusco T,Suu A L V,Perruchot S,Petit A,Tallon M,Thiébaut É,Boër M 2008Proc.SPIE7015 135

[31]Herman J R,Bass P 2008Proc.SPIE172 135

[32]Morris J R 1994J.Opt.Soc.Am.A11 832

[33]Sansonetti J E 2008J.Phys.Chem.Ref.Data37 1659

[34]Kramida A,Ralchenko Y,Reader J NIST Atomic Spectra Database http://physics nist gov/asd[2017-6-7]

[35]Auzinsh M,Budker D,Rochester S M 2010Optically Polarized Atoms(New York:Oxford University Press)pp198–252

[36]RochesterS M,HolzlöhnerR LGSBloch http://rochesterscientific/A D M/[2015-4-27]

[37]Kane T J,Hillman P D,Denman C A 2014SPIE Astronomical Telescopes+InstrumentationPalais des Congrès de Montréal,June 22–27,2014 p91483G

[38]Holzlöhner R,Calia D B,Budker D,Pfrommer T,Higbie J M 2012SPIE Astronomical Telescopes+Instrumentation,Amsterdam,July 1-6,2012 84470H

[39]Steck D A,Sodium D Line Data http://steck us/alkalidata[2010-12-23]

[40]Rochester S M,Atomic Density Matrix Package for Mathematica http://rochesterscientific/A D M/[2015-8-27]