对一道“绳联物体”运动的力学问题研究

陈玺君

(丹阳市吕叔湘中学 江苏 镇江 212300;

广西师范大学物理科学与技术学院 广西 桂林 541004)

1 引言

“绳联物体”指物体拉绳(杆)或绳(杆)拉物体的问题. “绳联物体”是高中物理一个较难的知识点，学生学习困难较大，也是各地高考、模拟、竞赛试题出题的热点.本文从一道“绳联物体”典例出发，剖析其中原理以期和读者共享.

2 问题引出

高一物理在运动的合成与分解问题这一节，教师往往都会举出这样一个“绳联物体”典型例题：

如图1所示，物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右做匀速直线运动的过程中，则( )

A.物体A也做匀速直线运动

B.绳子拉力始终大于物体A所受重力(0<

α<90°)

C.绳子对物体A的拉力逐渐增大

D.绳子对物体A的拉力逐渐减小

图1 题图

这是一道典型的绳的末端速度分解问题，处理上述问题的关键步骤是：

(1)找到物体B运动的合运动(如合速度、合位移、合加速度等，难易程度一般).

(2)寻找合运动的两个有效的分运动.(较难)

(3)使用平行四边形定则处理合运动与分运动的关系.

而高中物理教材(如人教版教材)中没有关于合运动的明确定义，这给学生寻找合运动造成一定困扰.笔者建议合运动可以这样感性地定义：眼睛观察到的物体的实际运动为合运动.如上题中眼睛观察到物体B是水平向右运动，因此物体B的合运动合速度水平向右.紧接着是如何将物体B的速度vB进行有效分解.绳的末端B点(即物体B的运动)可等效为参与了如下两个分运动：

(1)绳的末端B点绕滑轮(圆心)转动(做圆周运动).

(2)绳的末端B点沿绳方向伸长(或收缩)的直线运动.

有了这两个分运动的方向使用平行四边形定则分解唯一，如图2所示.

图2 用平行四边形定则分析图示

由图可知

v∥=vA=vBcosα

v⊥=vBsinα

则α减小，vA增大(单调递增)，故A向上加速运动，具有竖直向上的加速度，由牛顿第二定律可知

T-mg=maA

拉力T>mg，选项A错误，B正确.在处理C,D选项拉力的变化规律时，由于是变力，遇到了很大的挑战.笔者见到这样一种解法,受力分析如图3所示.由正交分解法可得

解得

由于α减小，因此拉力T减小.

图3 用正交分解法分析受力图示

这种解法看似完美，虽然拉力T减小的结论是正确的，但由于题目并未交代物体B与地面的动摩擦因数μ为定值，显然这种解法是不严谨的.

下面给出这道题定量细致的推导过程，以期获得教学方面的理论指导.

3 研究过程

3.1 速度关系和角速度关系

v∥=vA=vBcosα

(1)

v⊥=vBsinα

(2)

而

(3)

所以

(4)

式(1)、(2)、(4)表明，当α减小时，vA增大，v⊥和ω均减小.

若设m=0.1 kg,vB=2 m/s,h=5 m，则

在几何画板作图如图4所示.

图4 ω-α关系图

3.2 加速度关系

B向右运动过程中，α减小，故

(5)

(6)

将式(5)代入式(6)得

(7)

式(7)表明，当α减小时，aA减小.

若设m=0.1 kg,vB=2 m/s,h=5 m,则

在几何画板作图如图5所示.

图5 aA-α关系图

3.3 角加速度关系

(8)

式(8)表明，当α减小时，角加速度β先增大后减小.

若设m=0.1 kg,vB=2 m/s,h=5 m, 则

在几何画板作图如图6所示.

图6 β-α关系图

由以上分析可知：垂直于绳方向做的是线速度v⊥减小，角速度ω减小，角加速度β先增大后减小的变加速圆周运动.

3.4 位移关系

(9)

对式(9)积分有

(10)

可得

(11)

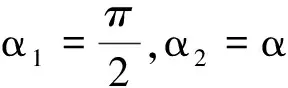
(12)

式(12)由几何关系亦可求出，结论一致.

若设m=0.1 kg,vB=2 m/s,h=5 m,则

在几何画板作图如图7所示.

图7 xA-α关系图

3.5 拉力(变力)关系

由牛顿第二定律知

T-mg=maA

(13)

故

(14)

可知，拉力T随α角的减小而减小.

若设m=0.1 kg,g=10 m/s2,vB=2 m/s,h=5 m,则

在几何画板作图如图8所示.

图8 T-α关系图

3.6 拉力(变力)做功关系

dWA=TdxA=

(15)

积分

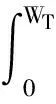
(16)

得

(17)

若设m=0.1 kg,g=10 m/s2,vB=2 m/s,h=5 m, 得

在几何画板作图如图9所示.

图9 WT-α关系图

此结论由功能关系亦可求得，结论一致，此处不再赘述.

通过以上分析可知，从运动的合成与分解的角度来看，物体B水平向右的匀速直线运动可等效为变加速圆周运动与变加速直线运动的合运动.

物体A做的是vA增大，aA减小的竖直向上的变加速直线运动,物体A发生超重现象.不仅拉力T大于重力mg，且拉力T随α角的减小而减小.

本题答案B,D.

4 其他思考

高中物理有没有什么方法来解决上述题目中拉力大小的变化规律呢？笔者见到不少高考复习资料上是这样解答的：若从极限的角度去理解，当α→0时，vA→vB，由此可推断A的速度越来越大，物体A最后做匀速运动，A的加速度为零，从而判断A的加速度随α角的减小而减小，似乎可以完美解决，但又带来一个思考，A的加速度是不是随着vA的增大而单调递减这个结论无法得知，显然不够严谨.

5 综述

5.1 处理方法

上述研究采用的主要物理方法有隔离法、理想模型法、运动的合成与分解法、微分法、积分法.

5.2 教学指导

“绳联物体”运动模型题是高中学生比较怕做的一类题型，教师在指导学生处理这一类问题时，务必要培养学生能够独立寻找合运动以及它的两个有效的分运动方法的能力.高中物理对于处理变力问题时要用到高等数学知识往往显得力不从心，如以上采用了正交分解法、极限思想等方法来变换处理，虽很巧妙，但思维不够严谨，假如教师能够从普通物理微分和积分的角度认清这类问题的本质和结论，然后再对上述模型进行特殊处理和加工，如以上正交分解法中可假设动摩擦因数μ恒定来分析，如此一来，既可以方便讨论，简化问题，又可以减轻学生负担，培养学生解题思维能力，对高中物理教学可以起到很好的理论指导的作用，真正促进高效物理课堂教学.

6 结束语

本文以“绳联物体”运动模型为例详实、细致地研究了这个力学问题，获得了这个问题的速度、加速度、力、功的关系，加深了对处理这一类问题的心理预期，使之不再停留在感性的认知上，通过理论分析产生对这一类问题的实践指导，为这一类问题的解答提供了一个理论指导，不足之处请指正.

1 漆安慎.普通物理学教程 力学学习指导书(第2版).北京：高等教育出版社，2009

2 王朝银.创新设计.昆明：云南人民出版社，2016.06

3 江苏省物理学会.物理学奥赛教程(增订本).南京:南京大学出版社,2004.06