追寻本真的数学课堂

张秀花

【摘要】 数学课堂应基于儿童认知、基于数学内容回归数学教育的本原以及体现数学教学的本质，重视培育学生的真兴趣，引导学生真探究，促进学生真建构，创建充满童趣和数学味的“本真课堂”，促进学生数学核心素养的形成，从而促进学生全面发展。

【关键词】本真；探究；建构；小学数学

随着新课改向纵深发展，追求真实有效的数学课堂已成为应然要求，老师们应基于儿童认知、基于数学内容回归数学教育的本原，体现数学教学的本质。创设丰富的活动，引导学生经历数学化的过程，重视数学思考，积累活动经验，渗透数学文化和数学思想方法，探究本真的数学课堂。一方面要充分利用并体现数学的学科特点，即数学课堂要充满“数学味”，让学生在学习过程中获得知识、能力、思想与方法等最为本真的东西；另一方面要依据并实现数学课程的真实目标，即重视培养“四基”，关注学生核心素养的形成，以真实、朴实、扎实的课堂培养身心健康、习惯良好、乐学善思、追求真理的“真人”，促进学生发展应成为数学教学的最终也是唯一的目标。

一、培育真兴趣

“兴趣是最好的老师。”数学课堂应培育学生的真兴趣，让学生真喜欢数学，真爱上数学。心理学认为，兴趣是直接推动学习的内在动力，是获取智能的开端、追求的先导、理想的桥梁，在人们认识和研究某种事物中起着十分重要的作用。正如赞科夫指出的：“兴趣是学习知识的能源，是发展智力的原动力。”激发学生的学习兴趣是调动学生学习的积极性、主动性的重要方面，是实现优质教学的有力保障。先来看一位老师执教《认识11—20各数》的精彩片段。

师：小朋友们，在上课之前，我们先来看一段动画片，还有10秒钟开始，我们一起来倒计时吧……（观看《爱探险的朵拉》视频，通过倒数10秒，帮助孩子复习10以内的数）

【第一环节： 认识计数单位“十”】

通过朵拉和智慧树的对话，引出树上一共有几颗星星。（播放录音）

1. 追问学生是怎样数的，掌握边数边做记号的方法。

2.摆小棒，认识几个一和1个十。

①用小棒摆一摆。提问：一根一根的摆了几个一根？

②老师再在黑板上摆，学生一起数。（板书：10个一）

③朵拉讲解：为了数得快，拿起来方便，我们通常将这样散开的10根小棒捆成1捆，它还有一个名字叫作1个十。（课件演示动态过程）

请大家将桌上的10根小棒捆成1捆，并举起来说是几个十。

提问：（左手拿一根）这是几根？（右手拿一捆）这是几捆？反复强调多说。 一捆就是一個十。（贴图板书）

接下来观察黑板上板书思考：10个1是几根小棒，1个十是几根小棒，它们相等吗？（板书：10个一就是1个十）追问：1个十里有几个一？（板书）

3.深化对计数单位“十”的认识。

认识计数单位“十”应用的广泛性和简便性。（课件演示，教师旁白）

朵拉：在生活中，我们也常常见到10。

师：10根羽毛球可以装成1筒，叫1个十，10支铅笔可以包成1包，也是1个十。如果王老师要买10个羽毛球或买10支铅笔，售货员可以怎样拿？有什么好处？（直接拿1筒或1包很方便）

4.认识“十”的另一种数学表现形式。（10个圈成一个圈）

师：刚才智慧树上的10颗星不好捆成1捆，我们可以用1个圈把它们合在一起也表示1个十。（课件显示）

【第二环节：认识十几的数】

1.认识12：通过帮蓝鸟找妈妈，朵拉又获得了两颗星星，现在朵拉有几颗星星？你会摆12根小棒吗？

学生比赛，动手操作，找学生展示摆法，并说一说是怎样想的。（通过预习，部分学生能很快地摆出一捆带两根的摆法）追问：为什么有一些学生没有摆好？（学生自己说可能是一根一根摆的，可能是把12根捆成一大捆）（通过比赛操作，让学生自己感受一捆带两根这种方便摆法）

2.运用方法，认识其他十几的数。

想不想接受朵拉的挑战？（这时孩子的兴趣非常浓厚）摆11和13，多让孩子说一说摆的方法。接下来让学生自己从14-19这些数中，选一个自己喜欢的数摆出来。观察所有小棒图，讨论：在用小棒摆11-19时，有什么相同点和不同点？

上述课堂教学过程中，教者先播放《爱探险的朵拉》的视频，将学生的积极性充分调动起来了，在整节课中将这个情境贯穿到底，使整个教学过程非常的完整。在教学过程中，教者给每个学生都准备了学具和资料，通过学生的动手操作，让学生亲身体验。通过摆一摆、数一数、说一说，把操作、观察语言表达紧密结合起来，突破了教学难点，使学生很好地建立了数位的概念，充分体现了数学学习的过程性和体验性。另外，整节课非常关注课堂的活跃性，让学生在玩中学，在乐中悟。教者为学生提供了许多有趣的活动，自主、合作等学习方式贯穿整节课，这样激趣的情境“润物无声”，构建了一个充满生机与活力的数学课堂。

二、亲历真探究

新课标指出，通过数学学习，学生要能获得必备的数学基础知识、基本技能、基本思想、基本活动经验；增强发现和提出、分析和解决问题的能力。数学课堂，应让学生在各自不同的知识基础，不同的生态位，丰盈知识的形成过程，让学生亲历真探究的过程，真正落实新课标提出的四基四能。如一位老师执教《认识厘米》时，让学生亲历了如下几个实践探究活动。

首先，量几厘米。（1）1号运动员跳了几厘米？（2）2号呢？展示三种不同测量方法，学生辨析。（3）问：在测量物体长度时，我们要注意些什么？

接着，量大约几厘米（课件呈现）。测量3、4、5号运动员跳远的长度，说明4号和5号都最接近7厘米，所以我们就可以说是大约7厘米。

试一试，身体尺大约几厘米。（1）尺子，真是个好工具！可是在古代没有尺子，人们怎么测量呢？想知道吗？古人很聪明，他们用的是身体上的尺子（课件呈现：一步、一拃、一庹。）然后，课件出示食指的宽大约是1厘米，这也是一把身体尺。手掌宽大约几厘米？课件出示测量方法，学生量一量。一拃呢？

然后，画几厘米。教者课件呈现场景，回到比赛现场，最后一名运动员上场了，它要冲刺冠军宝座，那它要跳几厘米才行？出示9厘米，学生画线段，再同桌之间交换检查。

最后，断尺量几厘米……

上述教学片断，教者以“跳远比赛”的情境为主线，把度量整厘米的长度、度量大约几厘米、估测几厘米和画几厘米的线段的教学串联起来，让学生经历观察、操作、想象、实践、交流等丰富多彩的体验活动，亲历真实的探究过程，在开放愉悦的课堂氛围中，通过看、找、比、量、画等学习活动形成1厘米的长度表象，进而认识几厘米，并引导学生在活动中掌握一些基本的测量方法和技能，快乐地解决一个个问题，生动且深刻地认识厘米。

三、促进真建构

皮亚杰的建构主义认为，知识不是通过教师传授得到，而是学习者在一定的情境即社会文化背景下借助学习是获取知识的过程其他人（包括教师和学习伙伴）的帮助，利用必要的学习资料通过意义建构的方式而获得。因此，数学课堂需要回到儿童学习本身，始终坚定儿童立场，坚持儿童学习取向，一切为了儿童发展，追求学习真正发生，有效建构数学知识。如一位老师执教《认识小数》时，呈现如下板块。

【板块一：“分”，小数出现了】

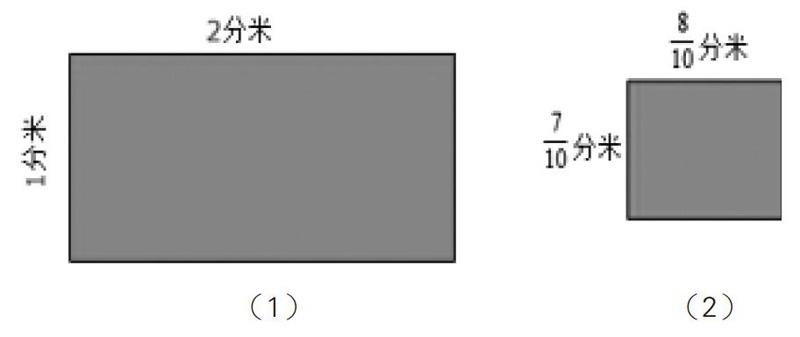
教者首先出示长方形（1），师生共同量出它的长和宽。接着出示长方形（2）。

提问：你还能像刚才那样一口报出它的准确长度吗？为什么不能？（因为长不足一分米）不足1分米时，我们可以用什么办法表示出它的准确长度呢？（生：以厘米为单位。生：可以用分数来表示）

提问：不管是以厘米为单位，还是用分数来表示，我们都是把这1分米怎样？（把1分米平均分成10份）为什么平均分成10份？（1分米等于10厘米）

长是多少？如果用分米做单位呢？可以用我們学过的哪个数来表示？宽呢？

比较：刚才我们测量了两个长方形的长和宽，都是以分米为单位，为什么第一个长方形的长和宽可以用整数表示，而第二个长方形的长度却要用分数来表示？当不足1分米的时候，整数就不好用了。我们就把1分米分一分，用分数来表示。我们的祖先很聪明，除了分数，还创造了新的数——小数。

【板块二：“合”，小数变大了】

0.8、0.2都小于1，小数都比1小吗？出示固体胶1元2角，提问：固体胶是多少元？你能试着用小数表示吗？（1.2元）你是怎么想到1.2元的？2角为什么是0.2元？

小结：1元和0.2元合起来就是1.2元。我们用一种新方法找到小数了！（课件出示：合）把整数1元和小数0.2元合起来得到一个新的小数1.2 元。

同学们能画图表示1.2吗？先出示一个正方形，提问：如果这个正方形表示1元，用它表示出1.2元行吗？再出示第2个正方形，现在呢？（够了）你打算怎么涂色表示，和你的同桌商量一下。

根据图，谁再来说一说1.2是怎样合成的？（1.2是由1和0.2合起来的）在1.2的基础上课件演示逐个增加一份，让学生说出小数，1.3、1.4、1.5、1.6……2，10个0.1又合成了1，加上前面的整数1，所以是2。如何用涂色部分表示出2.1元呢？（图形表示：整数2和小数0.1又合成一个小数2.1）

上述教学片段，首先通过“看图说小数”活动，将小数、分数知识有机地融为一体。通过数形结合，学生在对图形的比较、争论中，慢慢逼近小数的本质，深刻感受到小数与分数间的联系。第二板块中突出关键词“合”。教者紧扣分数和小数对应改写，突出小数意义的概括性理解。学生自主发现，把整数和纯小数合起来。在这个板块，通过“合”，从纯小数到带小数，进一步丰富了学生对小数的认识，让学生感受到数学的统一与和谐，逐步展现了一个全面而丰富的客观世界，在这当中，促进学生有效建构了“整数、分数、小数”数学知识网。

总之，数学课堂需要基于儿童年龄特征和认知发展规律，抓住数学学科本质，创设有趣的情境，引导学生真探究，促进知识真建构，创建充满童趣和数学味的课堂，促进学生数学核心素养的形成，从而促进学生全面发展。