基于干扰观测器的坦克炮控系统滑模控制

胡继辉， 侯远龙， 高 强， 陈宇政， 瞿生鹏

(南京理工大学机械工程学院，南京 210094)

0 引言

全电式坦克炮控系统是一种复杂的伺服系统，内部存在诸多非线性环节[1]，其中火炮身管和耳轴之间的摩擦力矩和负载扰动影响较大。在高机动作战时，摩擦转矩和负载转矩具有时变性，影响坦克炮控系统的稳定精度和低速性能[2-4]。主要体现在如下几个方面：低速情况下爬行现象显著；静摩擦具有多值性和离散性，速度过零时运动不稳定；系统的响应具有较大的静态误差和极限振荡现象[5]。现今坦克炮控系统大多被简化为线性定常系统进行建模[6]，采用经典控制理论进行控制，不能补偿摩擦非线性，控制效果达不到预期。文献[7]在研究摩擦模型的基础上，用基本滑模控制方法补偿摩擦非线性，虽然取得了较好的控制效果，但是由于简化的摩擦模型不具有实时性，因此控制策略有待完善;文献[8]采用自适应鲁棒控制策略对摩擦非线性进行补偿，既没有建立摩擦模型,也没有对摩擦转矩进行实时观测;文献[9]将摩擦转矩和负载转矩等外界扰动等效为有界总扰动，进行非线性补偿，缺乏对摩擦转矩和负载转矩补偿的精确性。针对当今研究存在的不足，对坦克炮控伺服系统进行建模，设计基于干扰观测器的滑模控制器。仿真表明，本文设计的控制策略既具有滑模控制对系统未建模动态强鲁棒性的优点，又削弱了抖振现象，且很好地补偿坦克高低向炮控系统的摩擦非线性和扰动负载转矩。

1 坦克炮控系统及其数学模型

1.1 坦克炮控系统结构

驱动坦克身管瞄准目标以及瞄准目标后维持身管的稳定是坦克炮控系统的主要功用[10]，由高低向和水平向伺服系统组成。按传动方式可分为电液式和全电式，电液式是传统的炮控系统，全电式是当今主流的发展方向[11]。全电式采用执行电机作为执行机构。本文对全电式坦克炮高低向伺服系统进行分析研究，被控装置主要包括交流电机、减速装置和身管，其结构框图如图1所示。

图1 全电式坦克炮高低向伺服系统结构框图Fig.1 Structure diagram of vertical servo system of all-electrical tank gun

1.2 坦克炮控系统的数学模型

传统的坦克炮控系统是由位置环、速度环和电流环组成的三闭环系统[12]，位置环响应速度慢导致系统稳态精度差，这是三闭环控制系统的固有缺点。本文研究的坦克炮控系统采用电流、转速双闭环控制系统，这也是当今坦克炮控系统的主流控制系统，其系统结构框图如图2所示。

图2 坦克炮控交流伺服系统结构框图Fig.2 Structure diagram of tank gun AC servo system

图2中:ωref为参考速度输入(角速度)；ω为坦克身管的角速度；GSR(s)为速度控制器；GCR(s)为电流控制器；uq为电流环输出电压；Ka为放大器增益(含功率放大器)；Ea为电机电枢反电动势；Ke为执行电机电磁转矩系数；L为电枢回路电感；Ki为q轴电流反馈系数；R为电枢回路电阻；Kω为身管角速度反馈系数；iq为q轴电流；Kt为执行电机力矩系数；Te为执行电机电磁转矩；Tf为摩擦转矩；TL为负载扰动力矩；ωm为电机角速度；B为粘性摩擦系数；J为电机转子上的总转动惯量；i为减速比。

根据图2的系统结构框图，可以得到坦克炮控系统的状态方程为

(1)

(2)

式中：TLS为摩擦转矩和变化的负载转矩。对式(1)进行拉普拉斯变换得

(3)

将式(3)代入式(2)得

(4)

(5)

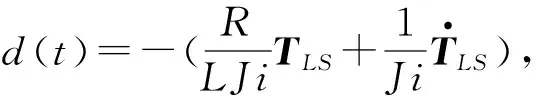
2 滑模变结构控制器设计

滑模变结构控制对系统外界扰动和系统内部参数变化具有好的鲁棒性[13]，因此在非线性系统控制方面具有很大的优越性。为了消除静差以及削弱抖振，设计滑模函数时引入了积分项。滑模函数设计为

(6)

式中：c1>0;c2>0。则

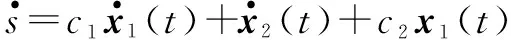
(7)

滑模运动包括沿着滑模面运动和趋近滑模面运动。趋近运动具体轨迹具有选择性，合理的趋近律不仅可以使系统以较快的响应速度运动到滑模面，而且到达滑模面时速度较小、抖振小。本文采用的指数趋近律具有以上优点，其表达式为

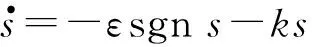
(8)

(9)

由式(7)和式(8)可得

(10)

将状态方程代入式(10)，进一步化简为

(11)

由式(11)可得控制量为

uq=b1(εsgns+ks+b2x1+b3x2+d(t))

(12)

3 干扰观测器设计

上述设计的控制量uq中含有摩擦转矩和负载转矩TLS，摩擦转矩和负载转矩是未知量，具有时变性，影响系统的动静态性能。设计干扰观测器观测TLS的变化，并反馈给控制量uq进行实时补偿。设计的干扰观测器结构框图如图3所示。

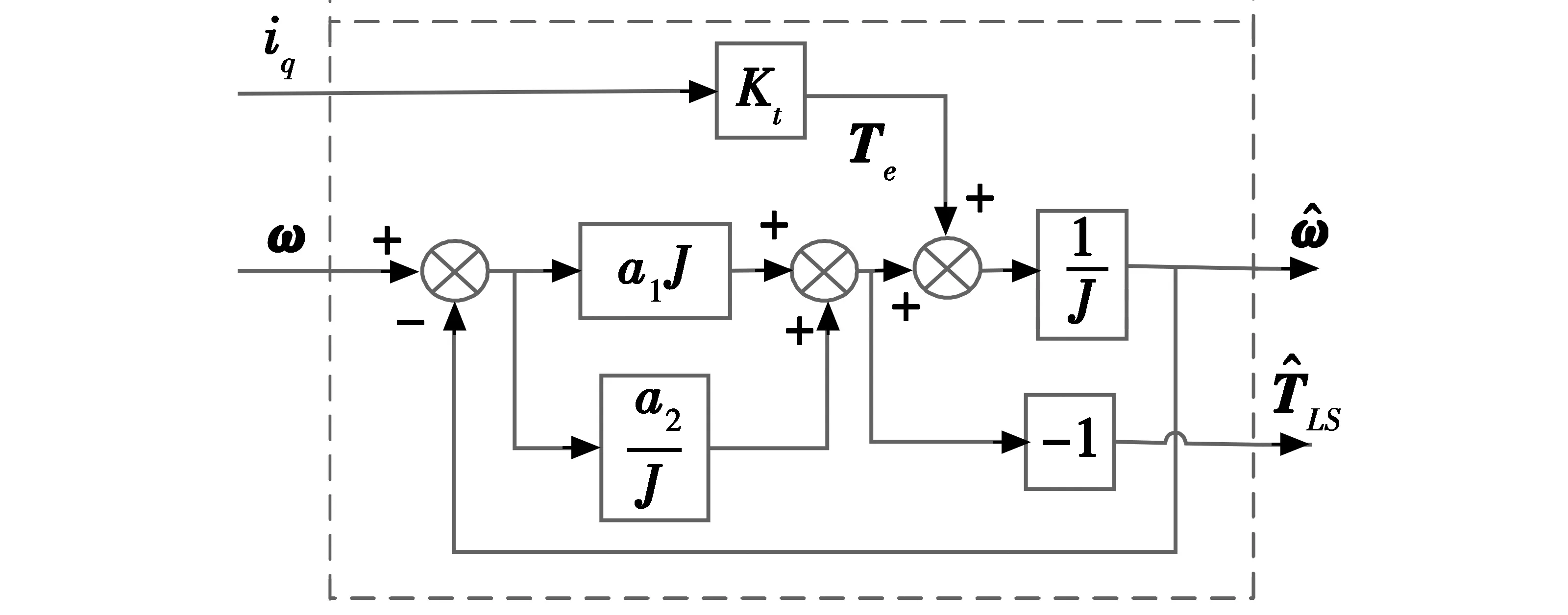
图3 干扰观测器结构框图Fig.3 Block diagram of disturbance observer

根据坦克炮控系统的结构框图，以及转矩平衡方程可得

J·dω/dt=Te-TLS。

(13)

设在较短时间内TLS的变化可以忽略，即

dTLS/dt=0 。

(14)

选取TLS和ω为观测变量，根据式(13)和式(14)可得

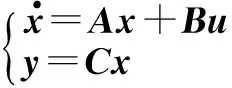
(15)

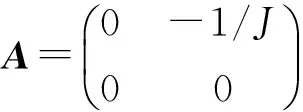
该干扰观测器的能观测性矩阵为

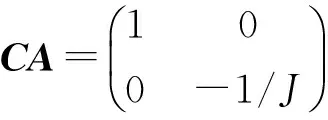
(16)

显然rank(CA)=2，和状态变量的个数相等，所以该系统完全可观。则系统的干扰观测器可以构造为

(17)

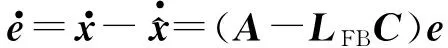
(18)

这里采用极点配置法来设计矩阵A-LFBC的特征值，使其具有负实部，从而能够保证观测误差最终趋近零。设配置的理想极点为a1，a2，此时特征方程可写为

s2-(a1+a2)s+a1a2=0 。

(19)

由式(18)和式(19)可得干扰观测器的特征方程为

(20)

由式(19)和式(20)可得

(21)

最终干扰观测器可表示为

(22)

4 仿真分析

本文提出的控制方法的有效性通过数值仿真来验证。仿真中用到的主要参数为：R=0.4 Ω，J=5239 kg·m2，i=1039，Kt=0.195 N·m/A，Ke=0.197 V/(rad·s-1)，L=2.907×10-3H。控制器中使用的参数如下：c1=20，c2=50，ε=0.03，k=0.005。干扰观测器的极点配置为：a1=-20+20i，a2=-20-20i。

为突显所设计控制策略的优越性，仿真比较了未对摩擦转矩和负载转矩补偿的简单滑模控制和基于干扰观测器的滑模控制在控制效果上的差别。图4是两种控制方法的系统速度阶跃响应；图5为系统静止时在4 s加入一个480 N·m的阶跃扰动的速度响应曲线；图6为简单滑模控制器的速度正弦跟踪曲线;图7为基于干扰观测器滑模控制器的速度正弦跟踪曲线。

从图4可知，未对摩擦转矩和负载转矩补偿的基本滑模控制在响应的初始阶段出现“停滞”现象，停滞时间大约为0.12 s。基于干扰观测器的滑模控制响应初始阶段未出现此现象，其响应时间为0.45 s，基本滑模控制的响应时间为0.92 s，设计的控制策略的阶跃响应远快于基本滑模控制。从局部放大图可以看出，基本滑模控制存在稳态误差且存在抖振现象，而基于干扰观测器的滑模控制削弱了抖振，稳态误差为零。从图5可知，在4 s加入一个480 N·m的阶跃扰动时，基于干扰观测器的滑模控制产生的速度偏差较小，且能够较快地恢复到目标速度，因此设计的控制策略具有更好的抗干扰能力。从图6基本滑模控制正弦跟踪曲线可知，由于未对摩擦转矩和负载转矩补偿，当速度过零时出现约为0.2 s的“爬行”现象，且跟踪性能较差。从图7可知，“爬行”现象被消除，且跟踪性能优越，因此提出的控制策略很好地补偿了摩擦非线性和负载扰动。

图4 控制系统速度阶跃响应曲线Fig.4 The speed step response curve of control system

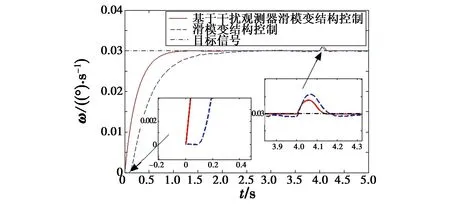
图5 加入负载扰动的速度阶跃响应曲线Fig.5 The speed step response curve with load disturbance

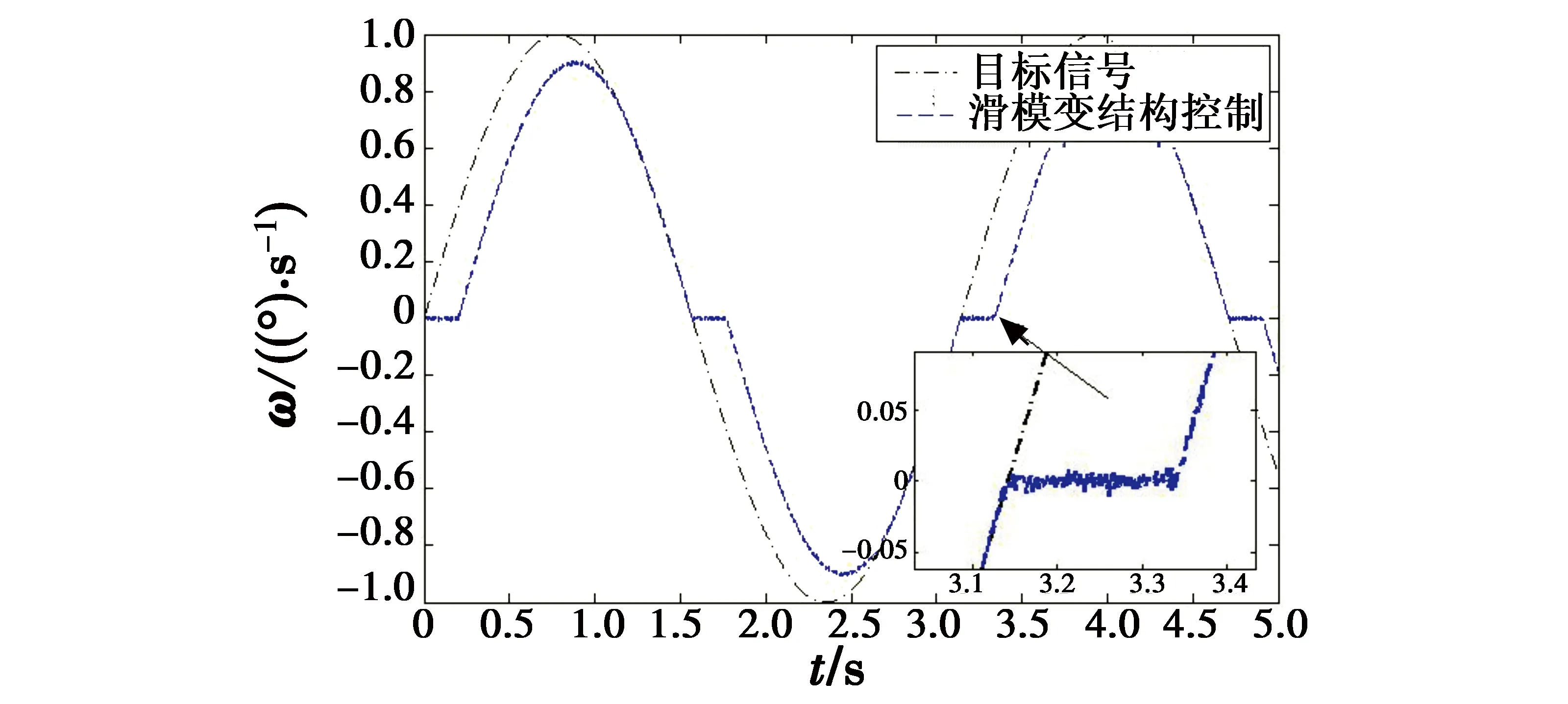
图6 滑模控制器的速度正弦跟踪曲线Fig.6 The sinusoidal velocity tracking curve of sliding mode controller

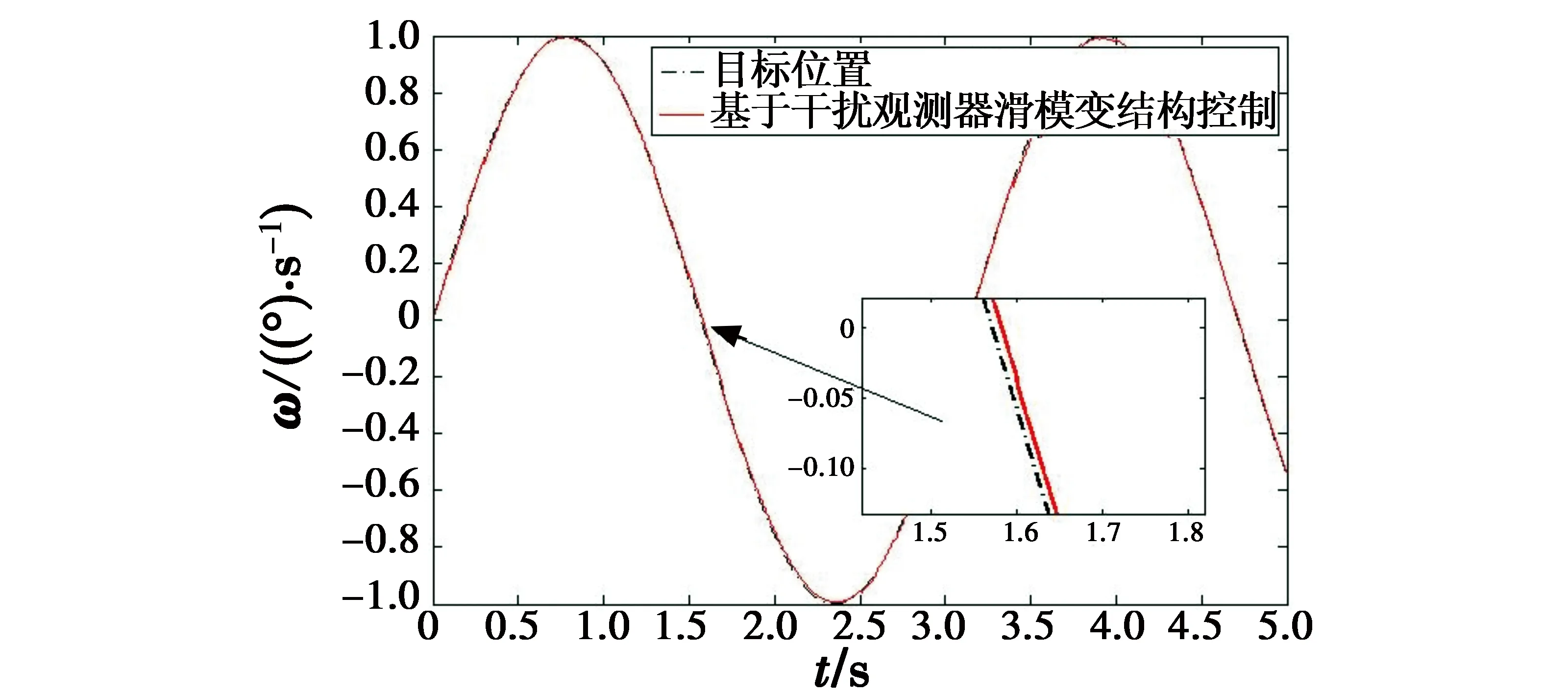
图7 基于干扰观测器的滑模控制器速度跟踪曲线Fig.7 The velocity tracking curve of sliding-mode controller based on disturbance observer

5 结论

针对坦克炮高低向系统存在的摩擦非线性和负载扰动的特征，提出基于干扰观测器的滑模变结构控制策略。通过仿真结果可以看出，设计的控制策略很好地补偿了坦克高低向炮控系统固有的摩擦非线性和时变负载转矩，基本消除了坦克身管在低速状态下的“爬行”现象。此外，干扰观测器对模型中未知量的观测，削弱了由于模型不确定性而引发的系统抖振现象。本文提出的控制策略具有实际应用前景，为坦克炮控系统补偿摩擦非线性和负载扰动提供了一个可行的方案。

[1] QIAO J H,WANG H Y.Backstepping control with nonlinear disturbance observer for tank gun control system[C]//Control and Decision Conference，IEEE,2011:251-254.

[2] WEI S,YUAN D,MA X,et al.Nonlinear backstepping sli-ding mode control for tank gun-control system[C]//The 2nd International Conference on Mechanic Automation and Control Engineering,IEEE,2011:7476-7478.

[3] 李娜,任一峰,赵敏.基于TC控制的坦克火炮系统的非线性研究[J].电子世界,2013(21):100-101.

[4] 沈陆娟,蔡建平.坦克炮控伺服系统的自适应鲁棒控制研究[J].数学的实践与认识,2012,42(7):170-175.

[5] ZHU Z K,MA X J,LI C B,et al.The analysis and control of low speed of all-electric tank gun control system[J].Acta Armamentarii,2011,32(8):1014-1018.

[6] 朱东旭,邱晓波,刘家健,等.坦克炮控系统摩擦扰动补偿研究[J].计算机测量与控制,2012,20(1):125-128.

[7] 冯亮,马晓军,冯东.坦克炮控伺服系统的滑模非线性摩擦补偿控制[J].火力与指挥控制,2008,33(12):63-65.

[8] 蔡建平,沈陆娟.坦克炮控伺服系统未知摩擦的自适应补偿控制[J].火力与指挥控制,2013,38(4):64-68.

[9] 黄志钢,翟明明.滑模变结构控制理论在坦克炮控系统上的应用[J].沈阳理工大学学报,2013,32(3):44-47.

[10] 马晓军,王福兴,袁东.全电式炮控系统非线性特性及其控制策略[J].装甲兵工程学院学报,2011,25(1):63-67，82.

[11] ZHU D,QIU X,WANG K,et al.Study on friction compensation for gun control system of tank based on ADRC[C]//The 2nd International Conference on Mechanic Automation and Control Engineering,IEEE,2011:1672-1675.

[12] 冯亮,马晓军,李华.基于扩张状态观测器滤波的坦克炮控系统模型参考自适应控制[J].兵工学报,2009,30(10):1375-1381.

[13] 王欢,王思明.带有干扰观测器的分数阶滑模控制[J].电光与控制,2015,22(5):89-92.