基于TSMC的四旋翼无人机抗风研究

王国贤， 随何虎

(武汉理工大学，武汉 430063)

0 引言

四旋翼无人机作为一种小型无人机，具有欠驱动、非线性、强耦合等特性，加之运行高度较低，易受风力干扰，其高控制精度的要求是目前研究面临的主要困难[1]。国内外科研人员对四旋翼无人机提出了多种控制方法方案，如PID控制、鲁棒控制、模糊控制、滑模控制和反步法等。文献[2-3]设计一种解耦PID四通道控制器，可实现有效的自稳定控制，但模型过于理想化，未考虑外界干扰；反步法需要精确的反馈控制才能满足系统稳定性[4];文献[5]采用传统滑模控制，取得了鲁棒性强、响应速度快的闭环控制系统,但将扰动作用在电机模块上模拟风场扰动难免会与实际情况存在一定误差。

本文建立四旋翼无人机在风场作用下的动力学模型，设计一种终端滑动模态控制器，并通过Matlab/Simulink软件进行仿真，验证了该控制器的鲁棒性与可靠性。

1 风场下的四旋翼无人机动力学模型

1.1 坐标系建立与变换

将无人机的飞行方向取为x轴，绕x,y,z轴旋转分别称为回转、俯仰与偏转，对应旋转角为α,β,γ，如图1所示。通过改变4个旋翼的转速，可以控制无人机实现偏转、回转和俯仰运动，使其以不同姿态进行飞行任务[6]。建立如图1所示的大地固定参考坐标系{G}OXYZ与机身坐标系{A}OAXAYAZA。机身坐标系{A}相对大地坐标系{G}的旋转变换矩阵为[7]

(1)

图1 四旋翼无人机模型结构图Fig.1 Structure of quad-rotor UAV model

1.2 风场下的四旋翼无人机受力分析

四旋翼无人机的飞行高度较低，易受到风场的干扰,其机身与旋翼的体积较小，可只考虑风力对旋翼旋转时空气流速的影响。无人机的升力来源为旋翼桨叶旋转时叶面上下空气流速不同产生的压强差，如图2所示。

图2 风场下旋翼的来流示意图Fig.2 The flow of a rotor in the wind field

各旋翼的拉力Fi的表达式为

(2)

式中：λ为升力系数；ni为各旋翼的旋转速率。

而风场环境会影响无人机的相对来流速度，改变旋翼上下叶面的压强差，故风场力的方向与升力方向相同，其表达式为

Fwi=2ρAVdiVw

(3)

(4)

式中：ρ表示空气密度；A表示桨叶扫过的面积;Vw表示各旋翼的诱导速度；Vdi表示风速；Fi表示各旋翼的拉力。

1.3 四旋翼无人机动力学模型建立

(5)

式中：m为无人机质量;E为3×3单位阵;I为三轴转动惯量矩阵。

借鉴前人的工作[8-10]并经过推导，可得四旋翼无人机在风场扰动作用下的动力学模型为

(6)

式中：Jr为旋翼旋转惯量；nr为各旋翼相对速率,nr=n2+n4-n1-n3;U1,U2,U3,U4为系统输入控制律，其表达式为

(7)

式中：l为质心到旋翼的距离；μ为阻力系数。

W为风场扰动向量，定义为

(8)

1.4 紊流风场模型的生成

通过成形滤波器将Gauss白噪声信号转化为大气紊流信号的Dryden模型模拟紊流风场[10],简化的成形滤波器的传递函数为

Gu(s)=Ku/(Tus+1)

(9)

Gv(s)=Kv/(Tvs+1)

(10)

Gw(s)=Kw/(Tws+1)

(11)

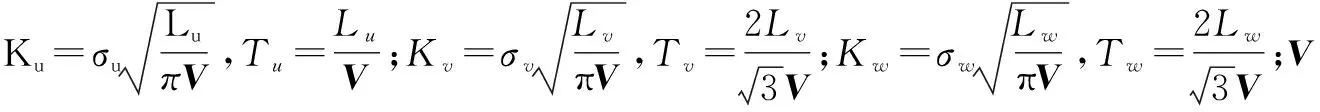
(12)

式中：h为无人机飞行高度；u为6.096 m高度的风速。

2 终端滑模控制器的建立

针对四旋翼无人机系统的欠驱动、非线性特点。设计一种快速TSMC的控制方法，具体为关于一种全局快速终端滑模控制器的设计。该控制方法具有以下优点：1) 综合了传统滑模控制与终端滑模控制的优点，不受外界干扰影响，并且适用于非线性系统；2) 可保证在有限时间内迅速到达滑模切换面，且收敛时间可进行调整；3) 该控制无切换项，有效消除了抖振。

(13)

其中过渡控制律为

(14)

图3所示为本文设计的控制系统结构图。设定四旋翼无人机的期望飞行参数(xd,yd,zd,αd，βd,γd)通过快速终端滑模控制器的算法计算出各个控制律，并将其输入至风场扰动作用下的四旋翼无人机的动力学模型中，产生的位置与姿态状态变量反馈至对应滑模切换面与控制律，从而控制四旋翼无人机的飞行。

图3 控制系统结构图Fig.3 Structure of control system

2.1 滑模切换面的设计

四旋翼无人机系统为二阶的非线性系统，以位置量x为例，设其预期和实际误差为ex=xd-x。根据全局快速终端滑模控制器定义取位置量x的误差滑模切换面为

(15)

设计全局快速滑模控制律为

(16)

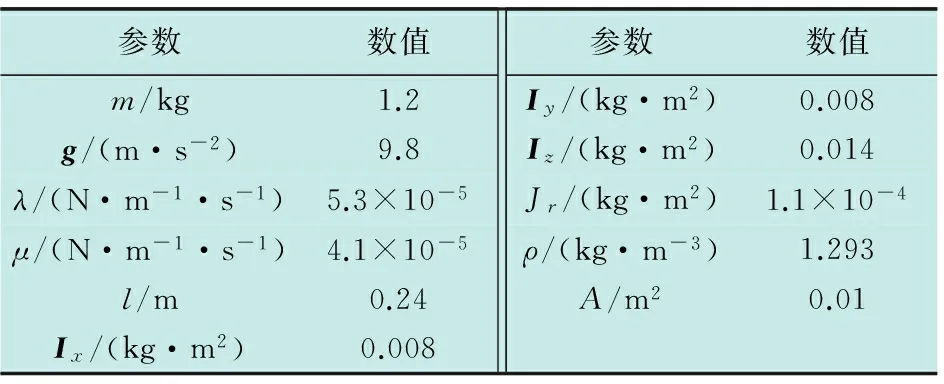
式中：i,j,h,k皆大于0；p

利用Lyapunov定律验证该滑模控制器的稳定性，选取Lyapunov函数

(17)

(18)

通过上述可证该控制器稳定，符合设计要求。

2.2 滑模控制律的设计

同上所述可得其余各位置与姿态量的误差滑模切换面为

(19)

其余各量的输入控制律为

(20)

3 系统仿真与分析

利用Matlab/Simulink软件搭建四旋翼无人机在风场扰动下的仿真系统模块框图，如图4所示，并进行仿真试验。

图4 仿真系统模块框图Fig.4 Block diagram of simulation system module

查阅相关文献设计出四旋翼无人机仿真需要的参数，如表1所示。

表1 四旋翼无人机仿真参数

同时，设紊流风场中6.096 m高度下的风速为10 m/s，全局快速终端滑模控制器的参数分别设定为i=0.5,j=h=k=1,p=5,q=9,p′=11,q′=15。设定四旋翼无人机的初始空间状态量为X=(0,-1,0,-1,0,1,-π/3,π/6,-π/3,-π/6,-π/2,π/6);期望位置为(xd,yd,zd)=(6,8,10)；期望姿态为(αd,βd,γd)=(0,0,0)。根据以上参数与数据的设定，仿真时长定为10 s，通过仿真得到如图5和图6的位置与姿态曲线。

图5 位置曲线Fig.5 Position curves

图6 姿态曲线Fig.6 Posture curves

由图5可以看出，四旋翼无人机在全局快速终端滑模控制器下从初始位置坐标(0 m,0 m,0 m)飞行到目标位置坐标(6 m,8 m,10 m)，在1.5 s时到达指定高度，4 s左右达到稳定状态并消除了抖振影响，实现定点悬停。以高度姿态为例，本文与文献[4-5,10]中各自得到的曲线相比较，全局快速终端滑模控制算法可在更短的收敛时间内运行更大的高度。对比文献[5]可以看出,本文的控制算法无切换项，比传统滑模算法更加有效地消除了抖振，受到风扰时曲线不会产生大的波动影响;与文献[10]采用的PD控制方法相比，本文算法得到的6条位姿曲线图的线条更加平滑。与其他文献比对后可得，本文采用的全局快速终端滑模控制器具有较强的鲁棒性与可靠性，适用于四旋翼无人机控制系统的设计。

4 结论

本文分析了四旋翼无人机的飞行控制原理与在风场作用下的受力情况，建立四旋翼无人机在紊流风场作用下的动力学模型，采用可自动消除抖振的全局快速终端滑模的控制算法计算各个控制律，并引入过渡输入控制律实现欠驱动耦合控制。通过Matlab/Simulink软件的仿真结果表明，该控制器算法具有可靠性高、收敛速度较快和鲁棒性较强的特点，能够有效地实现四旋翼无人机的飞行任务。

[1] 王贞琪，马洁.四旋翼几种控制方法比较[J].北京信息科技大学学报，2016,31(2)：35-39.

[2] 孟佳东,赵志刚.小型四旋翼无人机建模与控制仿真[J].兰州交通大学学报,2013,32(1):63-57.

[3] 江杰,冯旭光,苏建彬.四旋翼无人机仿真控制系统设计[J].电光与控制,2015,22(2):27-30.

[4] 牛洪芳,吴怀宇,陈洋.基于反步法的四旋翼飞行器滑动模态控制[J].高技术通讯，2016,25(12):1083-1090.

[5] 许喆.基于SMC的四旋翼无人机抗风扰研究[J].电光与控制,2017,24(1):67-71.

[6] 王小莉.面向桥梁检测的四旋翼飞行器控制系统研究[D].重庆:重庆交通大学,2013.

[7] NIKOLA G S,ANDON V T,OKYAY K.Comparative results on stabilization of the quad-rotor rotorcraft using bounded feedback controllers[J].Journal of Intelligent & Robotic Systems,2012,65(1):389-408.

[8] 孙妙平,刘静静,年晓红.基于区间矩阵的四旋翼无人机鲁棒跟踪控制[J].控制理论与应用,2017,34(2):1-11.

[9] BENALLEGUE A,MOKHTARI A,FRIDMAN L.High-order sliding-mode observer for a quadrotor UAV[J].International Journal of Robust and Nonlinear Control,2008,18(3):427-440.

[10] 吴翰文.四旋翼飞行器抗风控制研究[D].哈尔滨:哈尔滨工业大学,2016.