一种基于Red-Black小波的图像融合的改进算法

王虹元

(大连工业大学信息科学与工程学院，辽宁 大连 116034)

0 引言

为满足对一种场景的精确描述，一般会使用几种不同工作机理的图像传感器对场景进行成像，然后对这些成像信息进行特定算法的联合处理，即图像融合[1]。在遥感卫星图像融合方面，多光谱图像和SPOT全色图像的融合是目前研究热点，前者可以很好地保留图像的光谱信息，但空间分辨率较低，而后者则具有较好的空间分辨率特性，可弥补前者的缺点，所以将这两种图像进行融合一直是遥感图像融合领域的一个研究热点。

图像融合按照信息抽象程度可以分为像素级、特征级和决策级3个层次[2]。目前应用比较广泛的是基于像素级的融合算法，常见的有主成分分析法(PCA)[3]、分数阶样条小波(IHS)变换法[4]、小波变换法[5]及Brovey变换法[6]、离散小波变换法(DWT)[7-8]等。这几种算法在实际应用中均会存在一定的缺点，IHS变换法是最基础的算法之一，实现简单，但得到的融合图像的光谱信息损失很明显，这与融合图像应包含丰富信息的初衷相差较远。主成分分析法(PCA)可适用于遥感图像的所有波段，但在图像融合应用中，虽然可以增强图像的空间表现力，但计算量大，损失光谱分辨率较多。离散小波变换法应用于图像融合，由于对图像分解和重构的抽样处理，使得融合后的图像存在明显的方块效应，空间分辨率也较低。

近年来，图像融合的热点集中在对传统算法的改进以及将两种算法的结合上，如基于IHS变换和小波变换[8-9]的融合算法、小波变换和PCA相结合算法[10]、基于提升小波的融合方法[11-12]等，这些方法属于二维可分离小波，实现简单易操作，应用广泛。但是这类小波只能对图像的水平和垂直方向进行处理，并不能较好地提取图像的关键信息。GEERT[13]提出了一种不可分离小波，称为Red-Black小波变换，它是一种二维提升小波。

综上所述，本文将Red-Black小波和PCA相结合，用于遥感图像的融合。首先使用PCA提取图像的整体特征，即图像的主成分，然后对主成分进行Red-Black小波变换，并分别对小波变换后得到的高频和低频分量采用不同的方法进行融合。由于PCA将多个相关变量转换为少数几个变量，节省内存空间，而且对多光谱图像的所有波段都适用。Red-Black小波变换是将图像分解到不同的频域，而人的视网膜图像也是在不同的频率通道中进行处理的，这样就能获得更好的视觉效果。实验仿真表明，本文提出的算法既能提高图像清晰度，又可以较好地保留融合图像的光谱信息。

1 图像主分量的Red-Black小波变换

Red-Black小波变换分为水平/垂直和对角方向上的提升，每一个提升小波变换分为分解、预测和更新3个步骤[14]。

下面以8×8的图像X(i,j)说明Red-Black小波变换的基本原理。

1.1 水平/垂直提升

分解：将图像X(i,j)即λi+1分别按水平和垂直方向交叉分为红块λi和黑块γi,如图1a所示。

预测：利用水平和垂直方向4个邻域的红块来预测黑块的值，并且用此数值来替代黑块，那么图像的细节信息就存放在这个黑块中，如图1b所示，其算式为

(1)

更新：接下来利用水平和垂直方向4个邻域的黑块来预测红块的值，并且用此数值来替代红块，那么图像的近似信息就存放在这个红块之中，如图1c所示，其算式为

X(i,j+1)+X(i,j-1))imod 2=jmod 2。

(2)

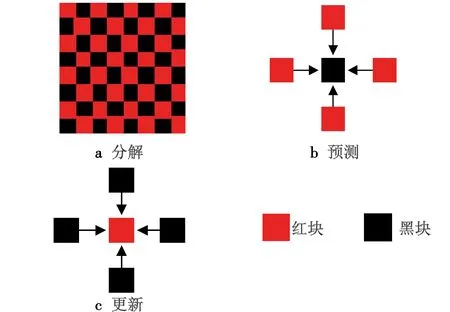
图1 水平/垂直提升Fig.1 Horizontal/vertical ascent

1.2 对角提升

分解：将水平/垂直提升步骤中的红块按照对角线方向交叉划分为蓝块系数和黄块系数两部分，见图2a。

图2 对角提升 Fig.2 Diagonal ascent

预测：由对角线方向4个邻域的蓝块系数值来预测黄块系数值，保存预测偏差到黄块中，如图2b所示,其算式为

X(i-1,j+1)+X(i+1,j-1))imod 2=1且jmod 2=1 。

(3)

更新：用预测偏差修正蓝块，使其保持原始图像的均值特性，如图2c所示,其算式为

X(i-1,j+1)+X(i+1,j-1))xmod 2=0且jmod 2=0 。

(4)

系数重排：为了图像更好地进行多分辨分析，在完成一次水平/垂直和对角提升步骤后，需要重新排列变换后的系数，如图3所示。

图3 系数重排Fig.3 Coefficient reordering

红黑小波的重构算法非常简单，只需要根据分解算法的变换系数交叉排列，对变换进行逆运算就可实现[14]。

2 基于Red-Black小波的遥感图像的改进融合算法

在对遥感图像的处理方面，多光谱MS图像可以很精细地保留图像的光谱信息，而SPOT全色PAN图像可以很好地保持图像的空间分辨率，因此这两种图像的融合一直备受关注。本文在对两种图像的融合算法上，采用PCA算法对图像的主成分进行处理，提取出图像的主要信息，然后再对主成分进行Red-Black小波变换。Red-Black小波变换作为不可分离小波，不仅可以消除行列方向的相关性，在水平和垂直方向上突出图像，而且可以消除对角线方向的相关性[15]，从而提取更多有用信息。经过红黑小波提升之后的图像信息被分成高频成分和低频成分，分别对其进行不同的算法处理，再进行红黑小波和PCA的逆变换，就可以得到带有更丰富信息的融合图像。

本文将Red-Black小波变换和PCA结合，综合Red-Black提升小波和PCA的优势，使用PCA进行图像融合的第一步，也即提取图像的主成分，再对主成分进行红黑小波变换，在节省计算量的同时，保证了图像的主要信息不丢失，而且还充分实现图像的细节信息的最优融合。

图4所示为PAN图像和MS图像的融合步骤，具体图像融合规则如下。

1) 首先将高分辨率PAN图像和MS图像进行预处理(包括几何校正以及精确配准等)，图像配准是不同遥感器、不同时相或不同方位的两幅或多幅图像之间建立起同名点间一一对应关系的过程，具体配准方法有多项式拟合法、共线方程法、随机场内插法等。

2) 分别对处理过的PAN图像和MS图像进行PCA变换，得到各自的第一主成分和第二、第三主成分：PC1，PC2，PC3和MC1，MC2，MC3。

3) 对第一主成分PC1和MC1进行Red-Black小波变换分别得到高频系数PSh,MSh以及低频系数PSl,MSl。

4) 在对低频成分进行处理时，一般采用加权平均的算法，但是该算法使得融合系数直接由单个系数的数值决定，这就导致融合后的图像存在边缘模糊现象。鉴于以上缺点，本文使用一种基于局域方差的融合规则，该算法可以很好地利用经过提升小波处理后的图像的低频系数的区域相关性，以能衡量区域相关性的区域方差为标准，得到融合后的图像的低频系数部分FFLW。

图4 基于Red-Black小波的遥感图像的改进融合算法Fig.4 The improved remote sensing image fusion algorithm based on Red-Black wavelet

首先对于权值α(d)满足

(5)

则局部方差为

(6)

式中：α(d)的大小和d点到b点的距离正相关，以此类推可以得到H(p,b)。

其次定义匹配矩阵为

(7)

式(7)中，低频图像的相关程度随着各点在[0,1]的取值范围内越大就越相关。若M(b)≤T，则

(8)

若M(b)>T，则

ψ(FFLW,b)=λMψ(M,b)+λPψ(P,d)

(9)

式中：T表示匹配阈值，取值范围为[0.5,1];λp=1/2-1/2((1-M(p)/(1-T));λM=1-λp。

5) 图像经提升小波变换后，高频分量反映图像的细节信息，包含了大量的图像边缘和纹理信息，对图像的清晰度有很大的影响。在各层的高频系数，采用基于极大值的选择规则[16]，得到融合后的高频系数FFH。

6) 利用上述步骤融合后的小波系数FFLW和FFH进行Red-Black小波重构，得到第K-1层的低频系数，然后将该系数与第K-1层的高频系数按照步骤4)和步骤5)进行融合，一直得到新的第一主成分FC1，其中小波分解级数K取3。

7) 将FC1代替步骤2)中的MC1，与图像的另外两个主成分MC2和MC3进行PCA反变换，得到最终的融合图像。

3 实验结果及分析

本文选取Land sat-TM多光谱图像与SPOT全色图像作为实验图像。图5、图6是实验结果。其中，图5a、图6a与图5b、图6b是MS图像、PAN图像的源图像，尺寸均为 512像素×512像素。图5c、图6c是利用PCA变换法[3]得到的融合图像;图5d、图6d是经IHS变换[4]得到的图像；图5e、图6e是利用加权平均(AVER)得到的图像，权值取0.5；图5f、图6f是利用小波变换法[17](WT)进行一级分解得到的图像；图5g、图6g是基于“Daubechies13”小波与PCA变换[18]相结合的算法(WT-PCA变换)得到的融合图像，分解级数为3级；图5h、图6h是基于本文的算法(RBWT-PCA变换)得到的融合图像，匹配阈值T取0.5。

图5 IKONOS融合图像Fig.5 IKONOS image fusion

图6 Land sat-TM和SPOT融合图像Fig.6 Land sat-TM and SPOT image fusion

3.1 主观评价

从视觉上看，经IHS和PCA变换得到的融合图像明显存在光谱信息扭曲、亮度不足，色彩发生了畸变；使用WT算法得到融合的图像较暗，存在方块效应；基于加权平均的图像融合方法得到的图像较为模糊，清晰度低，图像的轮廓和边缘细节表现上也存在明显不足；基于WT-PCA算法得到的图像亮度有所增加，使用RBWT-PCA变换得到的图像不仅具有良好的亮度，而且在图像边缘细节上都很清晰。

3.2 客观评价

由于人类视觉系统的缺陷及差异，所以有必要客观定量地分析融合后图像的效果。本文选取的评价指标有综合评价指数、扭曲度、清晰度、熵值[19-21]。表1和表2显示了各项指标的实验数据值。

表1 IKONOS多光谱图像与IKONOS全色图像

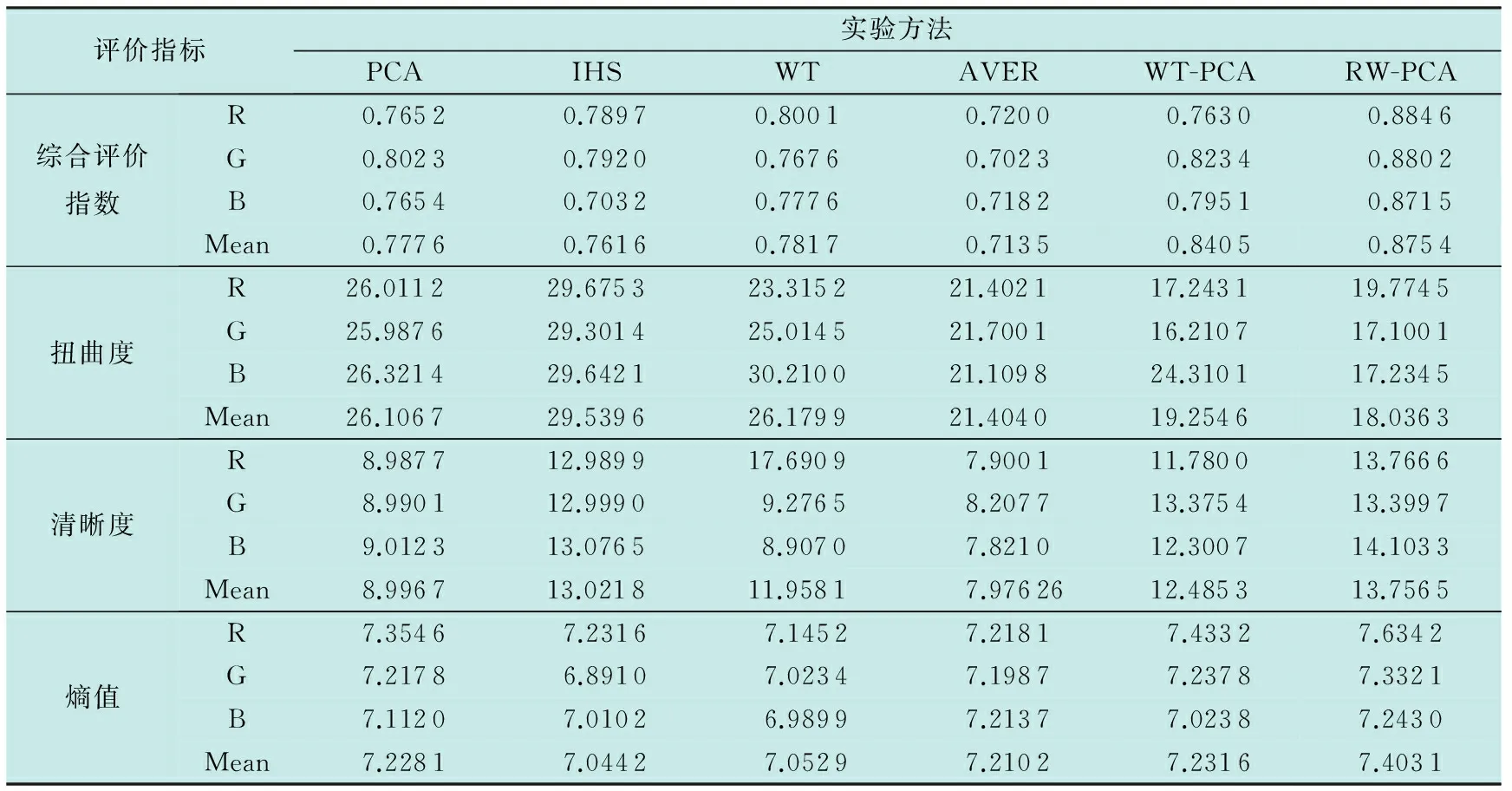
表2 Land sat-TM多光谱图像和SPOT融合图像

由表1和表2可以看出，利用本文算法得到的融合图像效果与其他方法相比,既保留了MS图像相对多的光谱信息,又表现了良好的清晰度，并且图像的熵值也是最大，表明图像包含了更多的信息。相比较而言，虽然加权平均算法扭曲度较低，但是融合后的图像的清晰度不高，这是因为加权平均同时模糊了两幅图像的细节部分，减少了原来图像轮廓和边缘的表现力，降低了图像的对比度；PCA变换则是用PAN图像的第一主成分替换掉MS图像的第一主成分，这样就使得融合后的图像的清晰度高，而扭曲度就比较大；IHS变换是将PAN图像直接置换MS图像的亮度分量，故融合后的图像产生了光谱退化现象；因此，综合考虑融合后图像的效果，本文算法在多光谱图像的融合方面具有显著改进。

4 实验结论

本文提出了一种基于Red-Black小波遥感图像的改进融合算法。该算法摒弃了传统小波依赖频率域、进行下采样、融合后的图像有方块效应等缺点，利用红黑小波具有同址运算优点，在具体实现时可省去大量存储的开销，而且提升小波在同等硬件条件下，对二维小波变换可节省3/4的时间，有利于系统实时处理。另外，该算法也结合了PCA可以对任意多个波段进行融合的优势。对于融合后的图像，从主观视觉上可以看出，利用本文的算法融合后的图像清晰，具有较多的光谱信息;从客观评价指标上看，该方法得到的融合图像信息熵优于其他算法，其在保持高分辨率信息和光谱信息的能力比基于PCA变换、IHS变换、WT-PCA变换算法都要优越。

[1] 陈立伟,蒋勇.图像融合算法的综合性能评价指标[J].计算机工程,2015,41(2):219-223.

[2] 余军.基于像素级的图像融合技术研究[D].上海:上海师范大学,2013.

[3] 魏旭.基于主成分分析的特征融合及其应用[D].成都：电子科技大学,2008.

[4] 刘红毅,韦志辉.基于分数阶样条小波与IHS变换的图像融合[J].南京理工大学学报:自然科学版,2006,30(1):81-84.

[5] 陈浩,王延杰.基于小波变换的图像融合技术研究[J].微电子学与计算机,2010,27(5):39-41.

[6] 聂倩,闫利,蔡元波.一种Brovey变换图像融合法的改进算法[J].测绘地理信息,2008,33(3):38-39.

[7] DESALE R P,VERMA S V.Study and analysis of PCA,DCT & DWT based image fusion techniques[C]//International Conference on Signal Processing Image Processing & Pattern Recognition， IEEE,2013:66-69.

[8] 刘贵喜,刘纯虎,凌文杰.一种基于小波多分辨率分解的图像融合新算法[J].光电子·激光,2004,15(3):344-347.

[9] CHEN S H,ZHANG R H,SU H B,et al.SAR and multispectral image fusion using generalized IHS transform based on à trous wavelet and EMD decompositions[J].IEEE Sensors Journal,2010,10 (3):737-745.

[10] 伊力哈木·亚尔买买提,谢丽蓉,孔军.基于PCA变换与小波变换的遥感图像融合方法[J].红外与激光工程,2014,43(7):2335-2340.

[11] ZHANG W,YANG J Z,WANG X H,et al.The fusion of remote image based on lifting wavelet transformation[J].Computer Information Science,2009，2(1):65-75.

[12] SUN F X,SUN D,YU Z X,et al.The fast image fusion based on a lifting wavelet algorithm[J].Intelligent Control and Automation,2004,5:4112-4116.

[13] GEERT U,ADHEMAR B.The red-black wavelet transform[C]//Signal Processing Symposium,IEEE,1998:191-194.

[14] 刘斌,祝青,彭嘉雄.基于Red-Black小波变换的多光谱图像融合方法[J].仪器仪表学报,2011,32(2):408-414.

[15] MOORTHI S M,GAMBHIR R K,MISRA I,et al.Adaptive stochastic gradient descent optimization in multi temporal satellite image registration[C]//Recent Advances in Intelligent Computational Systems,IEEE,2011:373-377.

[16] 李亚春，武金岗.小波变换图像融合规则性能的分研究[J].计算机工程与应用，2010,46(8):180-182.

[17] WU S,ZHAO B,BIAN M.A new fusion method of remote sensing images based on wavelet transform[C]//International Conference on Signal Processing,IEEE,2013:829-832.

[18] NAIDU V,RAOL J R.Pixel-level image fusion using wavelets and principal component analysis[J].Defence Science Journal,2008,58(3):338-352.

[19] LI S,YANG B,HU J.Performance comparison of diffe-rent multi-resolution transforms for image fusion[J].Information Fusion,2011,12(2):74-84.

[20] WANG Z,BOVIK A C.A universal image quality index[J].IEEE Signal Processing Letters,2002,9(3):81-84.

[21] LEUNG L W,KING B,VOHORA V.Comparison of image data fusion techniques using entropy and INI[C]//The 22nd Asian Conference on Remote Sensing,2001:132-139.