基于虚拟孔径扩展的非均匀稀疏阵DOA估计

韩佳辉， 毕大平， 陈 璐

(国防科技大学电子对抗学院，合肥 230037)

0 引言

波达方向(Direction of Arrival，DOA)估计是雷达对抗侦察领域的一重要研究方向。随着战场电磁环境日益复杂，传统的超分辨算法如MUSIC(Multiple Signal Classification)[1]算法已经不能满足作战要求。研究表明阵列DOA估计性能取决于阵列孔径的大小[2]，稀疏阵可以有效增加阵列孔径[3]。但当阵元间距大于信源半波长时会产生DOA估计模糊问题[4-5]。文献[6-8]提出利用Khatri-Rao(KR)积估计方法，可以估计大于阵元数目的信源，但是只适用于均匀线阵;文献[9-11]提出了稀疏嵌套阵列形式，但是阵列结构复杂，运算量大，实时性不好。针对以上问题，本文提出了基于虚拟孔径扩展的非均匀稀疏测向算法,该算法适用多种阵列形式，并且在进行虚拟孔径扩展的同时，将多快拍数据转换为单快拍数据，提高了计算速度。

1 MUSIC算法模型

如图1所示，考虑阵元数目为M的非均匀稀疏线阵，阵元位置坐标为z=(z1,z2,…,zM)。并且gcd(z1,z2,z3,…,zM)≤λ/2，gcd(·)表示求解最大公约数，λ为信号的工作波长。那么此阵列不存在角度模糊[12]。P个远场窄带不相关的信源以来波方向θi(i=1,2,…,P)入射到该阵列上，阵列的接收信号为

y(t)=Ax(t)+n(t)

(1)

(2)

(3)

由式(3)使θ变化，可通过寻找波峰来估计到达角。

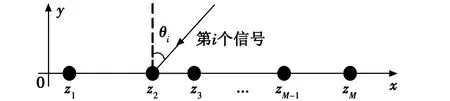
图1 非均匀线阵Fig.1 Non-uniform linear array

2 基于虚拟孔径扩展的DOA估计

2.1 虚拟孔径扩展思想

若信号与噪声之间互不相关，式(2)的阵列协方差矩阵可以写为

(4)

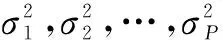
(5)

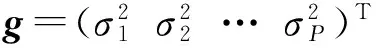
(6)

式中:⊗代表Kronecker积运算，导向矢量

a*(θi)⊗a(θi)=(ejωi(z1-z1)ejωi(z2-z1)…ejωi(zk-zj)…ejωi(zM-zM))T

(7)

式中:k=1,2,…,M;j=1,2,…,M。由此看出，经过KR积运算后，增加了大量虚拟阵元，阵元位置为集合{zk-zj,1≤k,j≤M}中不同的值，且不同值的个数远大于原阵元数M。比较扩展前的导向矢量，可知阵列孔径得到很大的扩展，阵列自由度增大。

(8)

(9)

2.2 任意阵列下的空间平滑算法

任意阵列下解决相干信号的空间平滑算法是基于阵列映射的思想，通过设计映射矩阵，将非均匀线阵映射为虚拟均匀线阵，然后使用空间平滑算法进行DOA估计。阵列映射的关键在于设计映射函数f(·)，使

(10)

(11)

(12)

(13)

(14)

xfl(t)=(xl(t)xl+1(t) …xl+N-1(t))T=
ANDl-1s(t)+nl(t) 1≤l≤L

(15)

式中：D=diag(ejω1ejω2… ejωP)为P×P维矩阵；AN=(aN(θ1)aN(θ2) …aN(θP))为N×P维的子阵阵列流形矩阵，其中,aN(θi)=(ejωiz1ejωiz2… ejωizM)T,i=1,2,…,P；nl(t)表示噪声矢量。则第l个前向子阵的协方差矩阵为

(16)

式中:RS为空间平滑前阵列协方差矩阵；σ2为噪声方差;IN为N×N维的单位矩阵。对L的子阵的协方差矩阵加权平均后，可得前向空间平滑协方差矩阵为

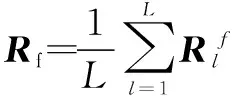
(17)

后向空间平滑的协方差矩阵为

Rb=J(Rf)*J

(18)

式中:(·)*代表复共轭;J是N×N维的反对角线元素为1其余元素均为0的置换矩阵。因此，可以前后向空间平滑协方差矩阵为

(19)

2.3 算法步骤

3 仿真实验

3.1 DOA估计分辨率性能

采用非均匀稀疏线阵，阵元数目M=4，阵元位置坐标z=[0,3,7,13]，两不相关窄带信号分别以θ1=-20°,θ2=20°两角度入射，信号波长λ=2。信噪比(SNR)为10 dB，快拍数500，采用本文算法与MUSIC算法得到的结果如图2所示。

从图2可以看出，对于来自θ1,θ2的两个窄带不相关信号，两种算法都能实现角度估计，但本文算法空间谱较MUSIC算法拥有更低的旁瓣，估计结果更好。

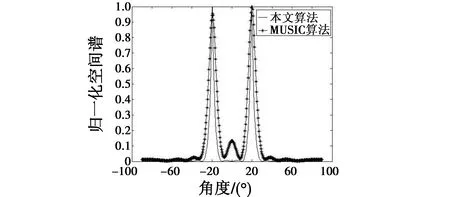
图2 本文算法与MUSIC算法DOA估计结果Fig.2 DOA estimation result of our algorithm and MUSIC algorithm

3.2 可估计信号个数

MUSIC算法采用阵元数目M=8，阵元位置坐标为z=[0,1,2,3,4,5,6,7]的均匀线阵。本文算法采用阵元数目M=4，阵元位置坐标z=[0,3,7,13]的非均匀稀疏线阵。信源数目P=6，窄带不相关信源分别以角度[-30°,-20°,-10°,0°,15°,25°]入射到这两个阵列上，信号波长λ=2。信噪比(SNR)为10 dB，快拍数500，两种算法得到的结果如图3和图4所示。

图3 MUSIC算法DOA估计结果(M=8,P=6)Fig.3 The DOA estimation result of MUSIC algorithm (M=8,P=6)

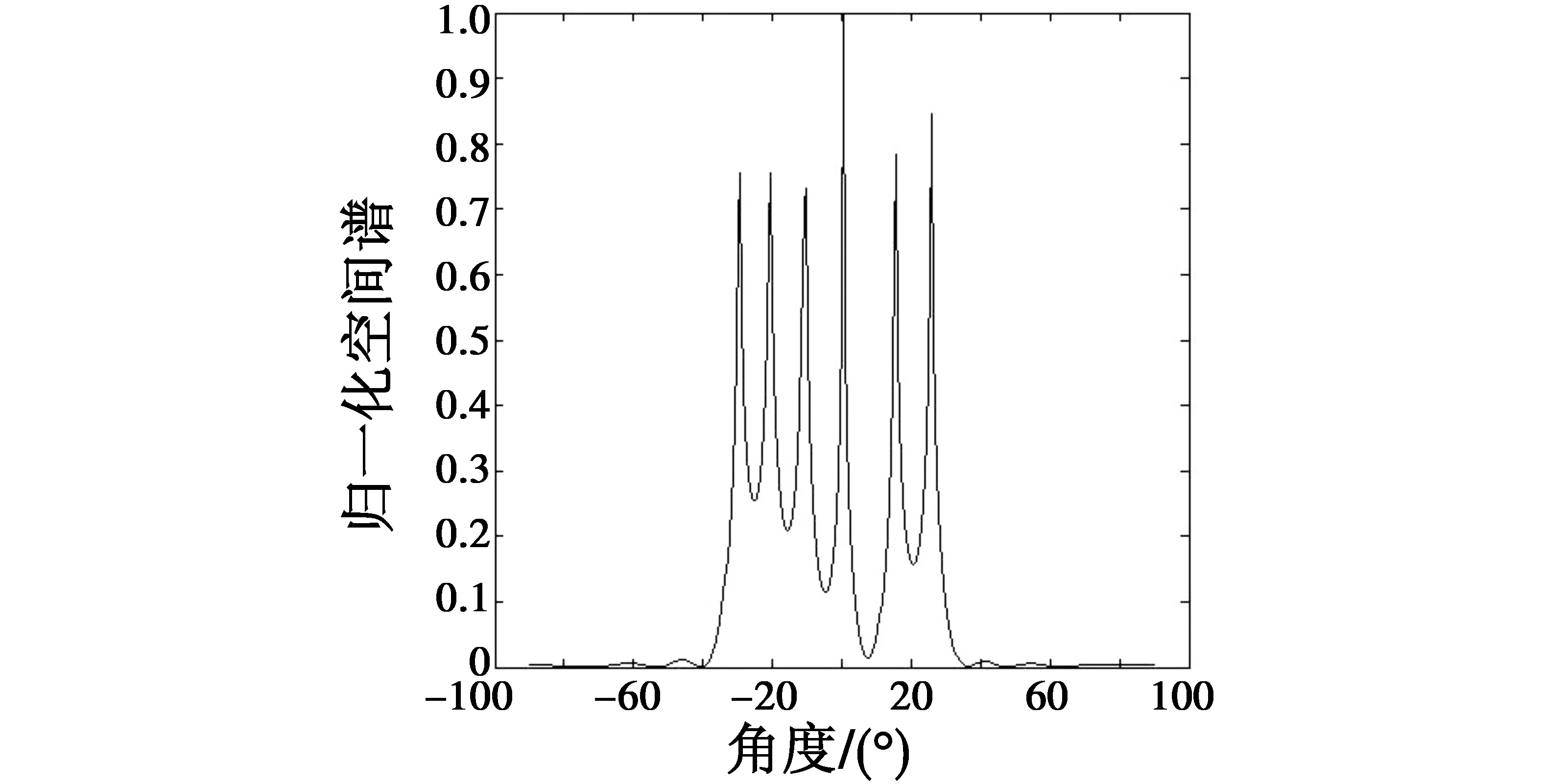
图4 本文算法DOA估计结果(M=4,P=6)Fig.4 The DOA estimation result of our algorithm (M=4,P=6)

从图3可以看出，在阵元数目小于信源数目的情况下， MUSIC算法不能有效地实现DOA估计。从图4结果可以看出，在信源数目大于阵元数目的情况下，本文算法可以无模糊地估计出信源DOA，并且空间谱旁瓣很低，角度分辨率很高。

3.3 均方根误差

采用非均匀稀疏线阵，阵元数目M=4，阵元位置坐标z=[0,3,7,13]。信号以θ=10°入射，信号波长λ=2。信噪比从-12 dB变化到6 dB，每2 dB做300次Monte-Carlo实验,快拍数500。比较信噪比对本文算法和MUSIC算法影响,结果如图5所示。

图5 均方根误差随信噪比变化Fig.5 Change of RMSE with SNR

从图5可以看出，当信噪比小于-8 dB时，本文算法仍然能够有效地实现DOA估计，而MUSIC算法性能急剧下降;当信噪比较高时，本文算法相较于空间平滑算法具有更低的均方根误差。

信噪比为0 dB，快拍数从0变化到300,其他条件同上。比较快拍数对本文算法和MUSIC算法影响，结果如图6所示。

图6 均方根误差随快拍数变化Fig.6 Change of RMSE with number of snapshots

从图6可以看出:在快拍数小于100大于50时，MUSIC算法性能急剧下降，本文算法能保持良好的估计性能;当快拍数大于100时，本文算法相较于MUSIC算法拥有更小的均方根误差，估计性能更好。

4 结论

本文针对常规均匀线阵DOA估计中可测信源数目不足的问题，提出了一种基于虚拟孔径扩展的非均匀稀疏阵测向算法。通过虚拟孔径扩展的原理，重构阵列接收信号协方差矩阵，然后结合任意阵列下的空间平滑算法实现DOA估计。仿真实验证明，相较于传统的MUSIC算法，本文算法有效扩展了阵列孔径，增加了阵列自由度，从而增加了可估计信源数目，在信源数大于阵元数时可以实现DOA估计。与传统MUSIC算法相比，角度分辨率有所提升，同时在低信噪比和小快拍情况下，具有较好的估计性能，并且本文算法对阵列形式限制较少，减少了天线设计难度，具有很高的应用价值。

[1] 司建伟.MUSIC算法多值模糊问题研究[J].系统工程与电子技术,2004,26(7):960-962.

[2] 邓佳欣,廖桂生,杨志伟,等.基于虚拟孔径扩展的子带信息融合宽带DOA估计[J].系统工程与电子技术,2016,38(2):245-250.

[3] ENGDABL C,SUNNERGREN P.Model-based adaptive detection and DOA estimation using separated sub-arrays[C]//IEEE Radar Conference,2004:104-109.

[4] 郭跃,王宏远,周陬.阵元间距对MUSIC算法的影响[J].电子学报,2007,35(9):1675-1679.

[5] 冷文,王安国.矢量修正解决DOA估计模糊问题[J].弹箭与制导学报,2010,30(3):155-158.

[6] 潘捷,周建江.基于凸优化的Khatri-Rao子空间宽带DOA估计[J].电子与信息学报,2013,35(1):80-84.

[7] PAL P,VAIDYANATHAN P P.Nested arrays:a novel approach to array processing with enhanced degrees of freedom[J].IEEE Transactions on Signal Processing,2010,58(8):4167-4181.

[8] 蔡晶晶,宗汝,蔡晖.基于空域平滑稀疏重构的DOA估计算法[J].电子与信息学报,2016,38(1):168-178.

[9] 谭伟杰,冯西安,张杨梅.基于Hankel矩阵分解的互素阵列高分辨目标定向[J].西南大学学报：自然科学版,2016,38(7):191-198.

[10] 王毅,陈伯孝,杨明磊,等.分布式nested阵列及其高精度DOA估计[J].系统工程与电子技术,2015,37(2):253-258.

[11] 邵华,苏卫民,顾红,等.多级嵌套L型阵列及其测向算法[J].宇航学报,2013,34(2):254-261.

[12] VAIDYANATHAN P P,PIYA P.Direct-MUSIC on sparse arrays[C]//International Conference on Signal Processing and Communications,IEEE,2012:1-5.

[13] 张聪,胡谋法,卢焕章.基于虚拟阵列空间平滑的相干信号DOA估计[J].电子学报,2010,38(4):929-933.