传输线多分支结构的阻抗匹配技术研究

付在明，王厚军，黄建国

(电子科技大学自动化工程学院 成都 611731)

无论对于高速数字信号的传输还是高频模拟信号的传输，其阻抗匹配是影响高频信号质量的主要因素之一[1]。阻抗匹配可以提高数字信号传输系统的可靠性和通信稳定性，而对于高频模拟信号(如矩形脉冲)而言，阻抗匹配能最大程度地降低信号失真[2-3]。其中，传输线技术的研究成为阻抗匹配技术的关键。文献[4]的“传输线基础”成为传输线技术的重要文献，促进了国内外传输线技术的飞速发展。平坦传输线结构、有损传输线、非线性传输线等的提出和研究不断丰富传输线理论，高频系统的应用使传输线阻抗匹配技术不断扩展和丰富[5-12]。而具有多分支结构特征的电路和传输线，在射频系统、微波系统中十分常见[13]。但在现有的文献中，基于阻抗匹配的基础理论体系和深入讨论这种特殊结构对信号的影响和精确的匹配计算却没有。因此，本文根据在高性能脉冲信号发生器研究过程中，对于射频通道模块的设计实践的总结，对该特殊结构的电路的阻抗匹配进行了深入分析。从传输线阻抗匹配的基本原理出发，分析研究了信号多分支结构的传输线特性和阻抗匹配条件，并对具有3个分支的传输线结构实例进行了仿真分析，并结合设计实践中的电流倍增电路(双分支)的实验结果，进一步总结了其他的影响因素，提出了传输线多分支结构阻抗匹配的基本解决方案和参数计算方法。

1 阻抗匹配原理

阻抗匹配是为了确保信号从源端传输到负载端整个路径上的阻抗连续性，以避免由于阻抗突变引起的信号反射，从而最大程度上解决过冲、振铃、上升沿退化等问题，同时满足输出功率最大化。阻抗连续是指源端输出阻抗、传输线特性阻抗、负载阻抗(接收器输入阻抗)相等。图1为一个典型的信号传输路径图[4]，它由驱动器、传输线、接收器组成。要保证阻抗连续，则需要满足条件信号才不会发生反射。其中RS表示源端输出阻抗，它由驱动器的电路结构决定，可以通过近端串联电阻的方式增大该值；Z0为传输线的特征阻抗，表示传输线恒定的瞬态阻抗，它仅与传输线的材料特性、介电常数和单位长度电容量有关系，与线长无关；为接收器输入阻抗。

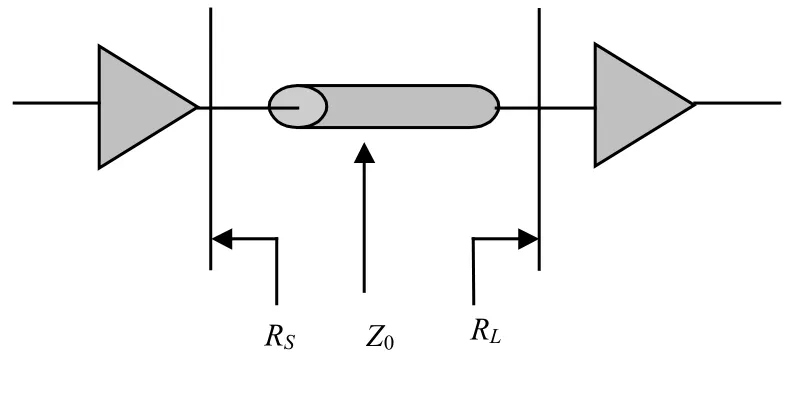
图1 信号传输路径示意图

当需要将源信号送到多个接收器(终端)时，信号传输路径将出现分支[13]。分支结构的阻抗匹配是以信号传输路径上阻抗的连续性为设计目标。在多分支结构的阻抗匹配中，由于信号传输路径上电路分支的存在，使得实现传输线上阻抗连续变得更加困难。在实际电路中，各分支点的反射情况比单点反射情况要复杂得多，同时各分支的拓扑结构或传输线长度的不同都会带来许多问题。

2 多分支结构特性

信号多分支结构是指一个驱动器或者信号源的输出被连接到多个驱动器或者负载上的一种特殊的信号传输路径结构。当信号频率高、上升时间短、传输线超过临界长度时，就必须对这种信号传输多分支结构中各支路的阻抗进行匹配。如图2所示的一个实例，一个驱动器输出被连接到3个接收器的多分支结构电路中，表示信号传输路径上的节点，则分别表示各节点之间传输线的特性阻抗，分别表示3个接收器的输入阻抗或者负载阻抗。当信号从驱动器输出，信号通过传输线网络时，不断感受到传输线上的瞬态阻抗的变化情况，一旦瞬态阻抗发生突变，信号就会在变化处发生反射，从而使接收端获得的信号失真。

图2所示的多分支结构中，信号通过节点A0到达节点A1处，信号出现分支，两个分支路径带来的阻抗突变(整体效果)将决定信号向A3、A2传播的总能量和从A1反射回去的能量，而传输给两个分支的能量分配则决定于分支的负载阻抗与传输线特性阻抗情况；在A2节点处信号表现出的传输特性与A1处相似。当任何一个支路的传输线特性阻抗与负载阻抗不相等时，该支路就会发生信号反射，反射信号回到前一个节点，向所有的其他支路传输，形成反射震荡。因此，任何一个支路阻抗失配引起的信号反射，会叠加到每一个支路信号上。

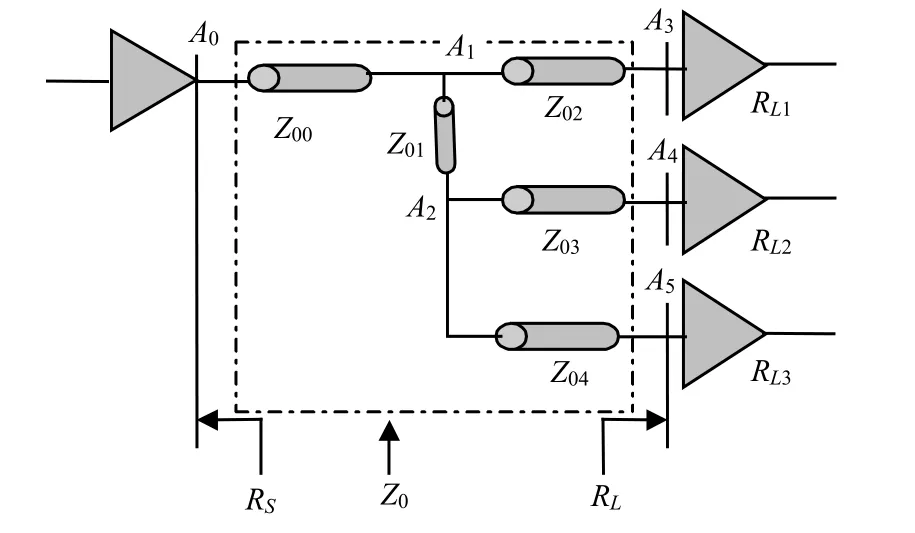
图2 三路传输分支的结构模型

3 多分支结构阻抗分析

多分支结构的阻抗匹配中，驱动器的输出阻抗为Rs，负载阻抗则为各分支端接收器输入阻抗的并联分支结构中由于多支路的存在，也就存在多段不同的传输线，每两个不同节点之间的连接线都是一段独立的传输线[13]。每一段传输线的特性阻抗需要根据节点两端阻抗连续的原则进行阻抗控制。在信号传输出现分支的节点处，分支电路表现出来的总体特性阻抗需要根据具体的分支与节点分布情况进行计算，本文以图2的三分支结构模型为例进行说明。根据文献[14]的研究成果，如果用传输线的零阶模型来计算特性阻抗，则该值为：

式中，Z0为传输线特性阻抗；CL为传输线单位长度电容量；εr为材料的介电常数。出现分支节点处，如图2中的节点，信号在到达A1前一瞬间遇到的传输线瞬态阻抗为Z00，过A1后的一瞬间遇到的瞬态阻抗为Z01与Z02的共同作用。传输线Z01、Z02是均匀的，则在A1的分界面两个分支对原信号的瞬态阻抗可以用它们各自特性阻抗Z01和Z02来表示。分界面处的瞬态阻抗设为Z0A1+，分界面之后单位长度的电容量设为CL′，两条支路的传输线单位长度电容量分别为CL1与CL2。顺着信号路径方向，从A1向后看过去，两支路传输线单位长度电容量CL1与CL2为并联结构，因此得到式(2)。由式(2)和式(3)可以看出，节点A1后的瞬态阻抗为

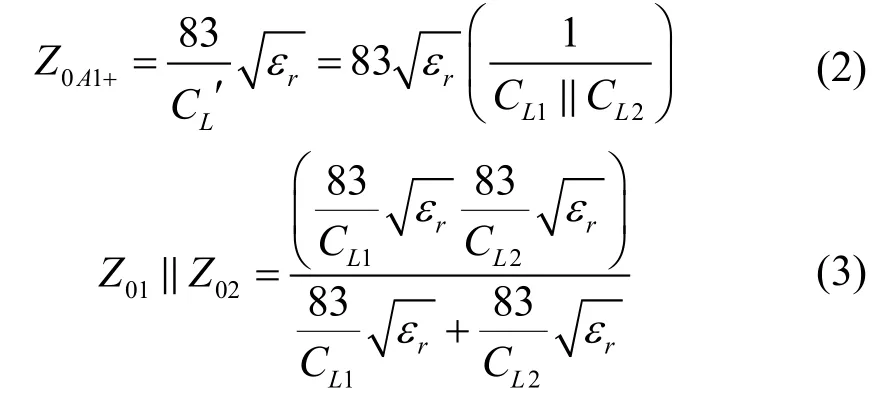
因此，图2中多分支结构模型的阻抗匹配必须满足式(4)和式(5)：

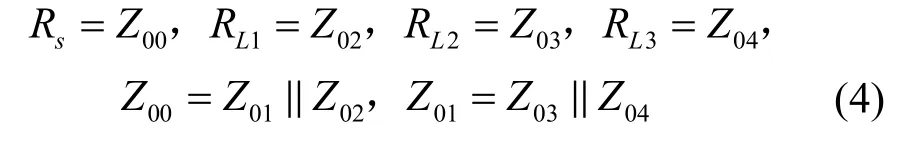
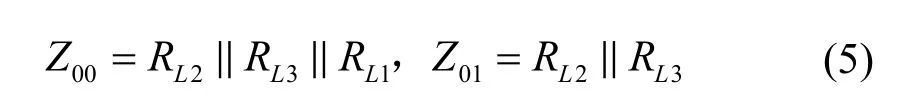
4 多分支结构信号仿真

以图2中所示三分支结构的分析为例，假设一个具有较低输出阻抗的信号源需要同时驱动3个同为90 Ω的负载，则按照第3节所述计算各分支传输线的阻抗匹配。由于负载是阻抗匹配的起点，因此传输线阻抗的推导应按节点从负载端逐次向源端进行计算。根据式(4)得到各分支的传输线阻抗应等于该分支的负载，因此设定图3中3个分支的传输线阻抗同为90 Ω，进而根据所选板材等参数计算得到具体的传输线宽度和厚度，同时必须保证同一面微带线的厚度相同，以便于加工。

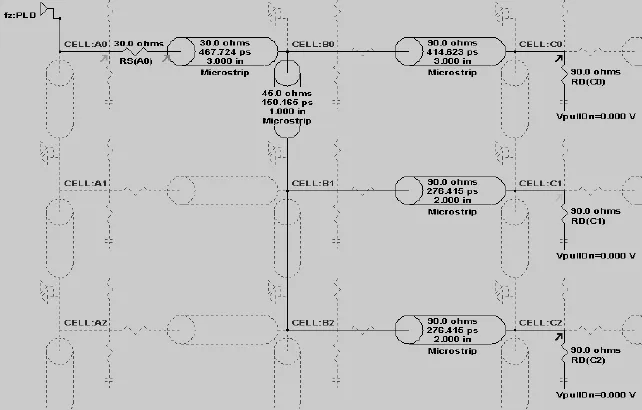
图3 多分支结构仿真电路图

图3中，第2分支(CELL：B1)、第3分支(CELL：B2)汇于一个节点后再与分支1汇合于另一节点，因此在计算这两个节点之间的传输线阻抗时，必须将分支2、分支3作为一个整体并按式(5)中的计算方法得到为45 Ω(即90 Ω∥90 Ω=45 Ω)计算。计算从源端到第一个节点(分支节点)之间的传输线阻抗时，把节点后的所有负载作为一个整体，计算结果为30 Ω(即90 Ω∥45 Ω=30 Ω)。由于源端输出阻抗较低，为了实现源端阻抗的匹配须串接一个电阻达到式(4)所示条件。因此，根据可计算得到源端串联电阻的值，其中RS为所需源端阻抗，R0为实际输出阻抗。另外，为了更好地保证信号不失真，减小分支反射的多重叠加，各分支与源端的延迟应尽量保持一致，如图3中传输线长度设置。利用Hyperlynx的LineSim对图3中信号多分支结构进行信号传输仿真，仿真信号为400 MHz的矩形波，仿真结果如图4所示。另外，如果改变图3中的各支路的传输线阻抗为60 Ω，则得到不满足匹配条件的多分支结构仿真波形如图5所示。

图4中波形“∆”为图3中A0点测得的源信号，波形“×”为负载上测得的重叠信号(因为每个支路的传输线长度相等)。从图4中可以看到，负载端信号上升沿基本保持了线性，高低电平非常平坦，具有较小过冲和振铃。将图3中第一个支路的传输线阻抗由90 Ω改为60 Ω后则得到图5所示仿真波形，负载所获得的脉冲波形失真严重，同时其他两条支路上也产生了信号失真。对比图4和图5，当多分支结构满足式(4)、式(5)的条件时，信号传输线阻抗匹配良好。

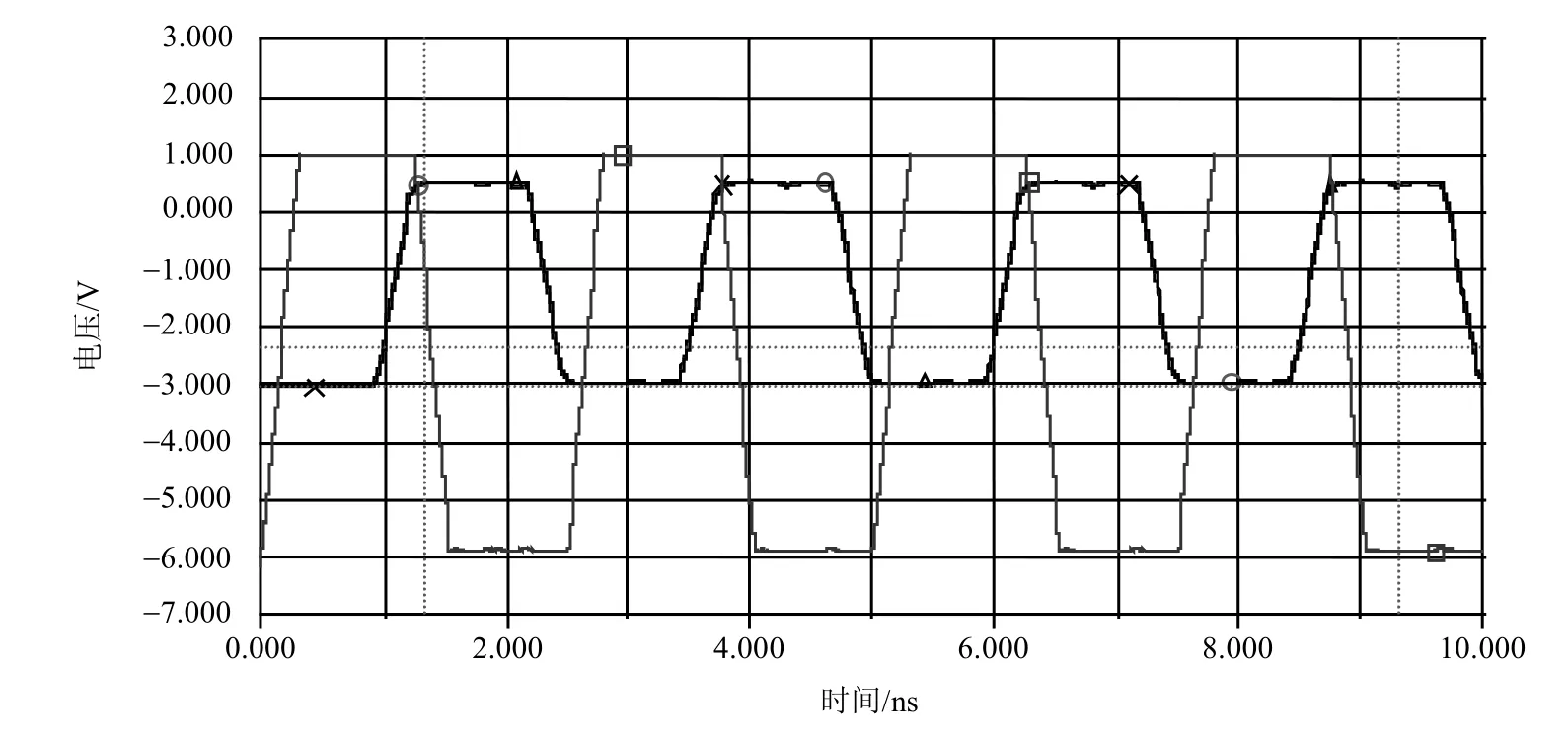
图4 满足匹配条件的多分支结构仿真波形

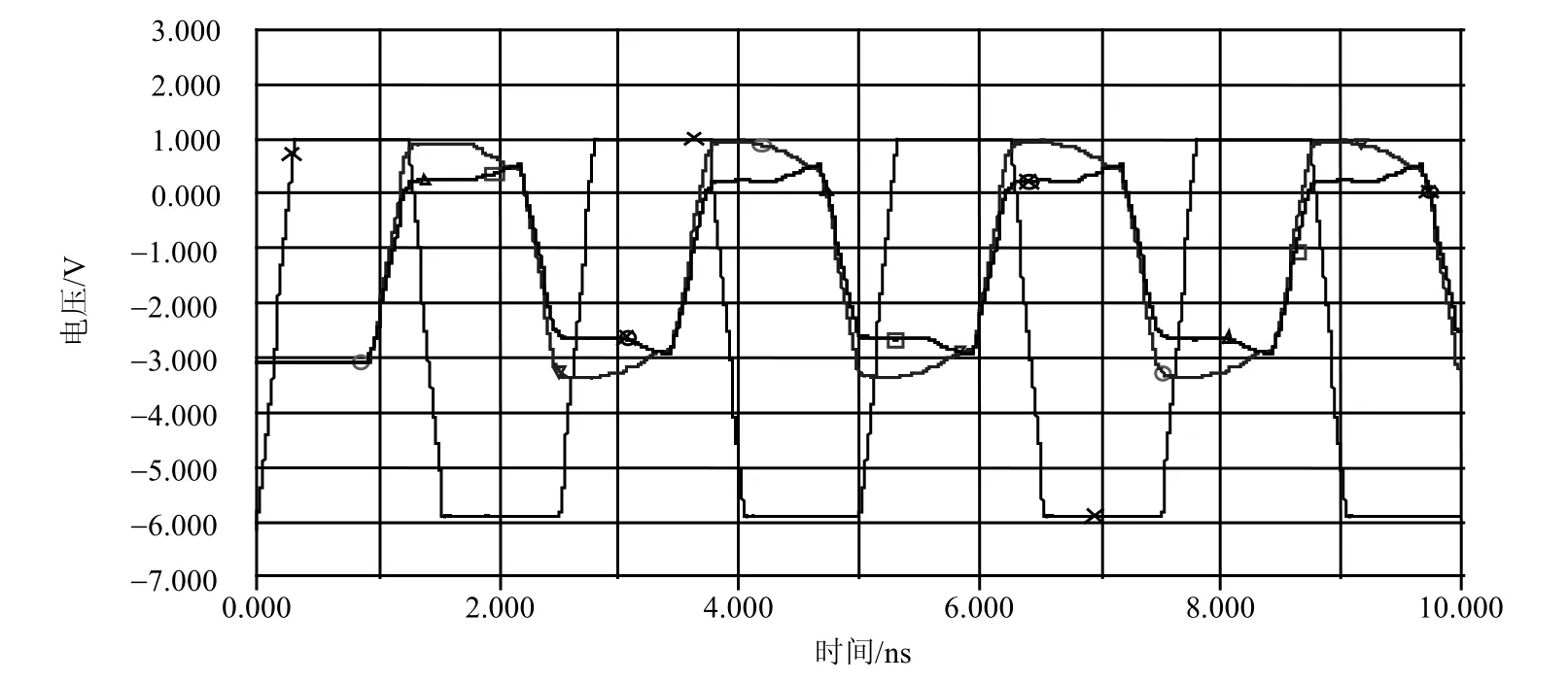
图5 不满足匹配条件的多分支结构仿真波形

5 结束语

经过不同条件下的多分支结构信号进行仿真和试验比较，并通过在非线性脉冲放大电路中的应用分析，在采用多分支结构的电路中可以按照以下方法完成阻抗匹配。首先根据接收端的幅度要求计算得到驱动器源端阻抗与接收端之间的阻抗比例，通过源端串联阻抗、接收端并联阻抗(或者串联)的方式使得源端阻抗与各分支的并联阻抗相等，并尽量使各支路的负载相等。然后根据各支路的负载计算该支路的传输线特性阻抗，继而得到分支点之前各段传输线的特性阻抗，并尽量使各段传输线长度小于临界长度，否则为了减小局部反射给其他支路带来的影响应该使各支路传输线长度相等(图2中A1到A4长度等于A1到A3长度)。如果某条支路连接线长度小于临界长度，分支节点前的传输线特性阻抗值需要式(5)来计算。如果某条支路的负载远大于RS，该支路需要作为桩线来考虑，传输线必须要小于临界长度。

[1]陈建华.PCB传输线信号完整性及电磁兼容特性研究[D].西安: 西安电子科技大学, 2010.CHEN Jian-hua.Study on singal integrity and EMC characteristics of PCB transmission lines[D].Xi’an: Xidian University, 2010.

[2]何彭, 何为, 苏新虹, 等.基于HFSS研究PCB传输线的信号完整性分析[C]//2014中日电子电路秋季大会暨秋季国际PCB技术/信息论坛论文集.东莞, 广东: 中国音质电路行业协会, 2014: 10-15.HE Peng, HE Wei, SU Xin-hong, et al.Research about signal integrity problem of high-speed PCB based on HFSS[C]//2014 China-Japan Electronics Fall Conference &Autumn International PCB Technology/Information Forum Proceedings.Dongguan, Guangdong: China Sound Quality Circuit Industry Association, 2014: 10-15.

[3]杨清熙，王庆国，周星, 等.基于PSPICE建模仿真方法研究传输线网络时域响应[C]//中国物理学会第十九届全国静电学术会议论文集.太原: 中国物理学会静电专业委员会, 2014: 254-261.YANG Qing-xi, WANG Qing-guo, ZHOU Xing, et al.PSPICE simulation method of transmission-line networks responses to electromagmetic pluse[C]//The Nineteenth National Academic Conference of electrostatic of China Physical Society.Taiyuan: Chinese Physics Society Electrostatic Professional Committee, 2014: 254-261.

[4]ANDERSON E M.Eletric transmission line fundamentals reston[M].Reston, VA: Reston Pulbishing Company Inc,1985: 1-4.

[5]ITOH T.Planar transmission line structures[M].Piscataway,NJ: IEEE, 1987: 1-3.

[6]GARDIAL F.Lossy transmission lines[M].Norwood, MA:Artech House, 1987: 6-32.

[7]HALL S H, HALL GW, MCCALL J A.High speed digital system design[M].Hoboken, NJ: John Wiley and Sons,2000: 1-48.

[8]CHIPMAN R A.Signal and power intergrity in digital systems[M].Columbus, OH: McGraw-Hill Book Company,1995: 35-78.

[9]LOBOS T, REZMER J.Waelet transforms for real-time estimation of transmission line impedance under transient conditions[J].Electrical Engineering, 2002, 84(2): 63-67.

[10]GARCIA N, ACHA E.Transmission line model with frequency dependency and propagation effects: a model order reduction and state-space approch[C]//Power &Energy Society General Meeting-Conversion & Delivery of Electrical Energy in the Century.Pittsburgh, PA, USA:IEEE, 2008: 1-7.

[11]STEVEN R.Best, shunt-stub-line impedance matching: a wave reflection analysis tutorial[J].IEEE Antennas &Propagation Magazine, 2002, 44(1): 76-86.

[12]LIAO Yong, XU Gang, XIE Ping.Numerical simulation of non-linear transmission line[J].High Power Laser and Particle Beams, 2015, 27(8): 1-5.

[13]BROOKS D.Controlling impedances when nets branch out[R].[S.l.]: UltraCAD Design Inc, 2005: 1-6.

[14]BOGATIN E.Signal integrity：Simplified[M].Upper Saddle River, NJ, USA: Pretice Hall PTR, 2003: 235-312.