多元伪泊松混合分布模型的理论研究

陈奕延 李 晔, 张淑芬

1(英国系统科学学会 伦敦 CR82AD)

2(北京理工大学自动化学院 北京 100081)

3(华北理工大学 河北省数据科学与应用重点实验室 唐山 063210)

1 引 言

混合分布模型是一类源于数理统计知识理论的数学模型，在股票、期货、风险管理、健康产业、保费厘定、电力工业、生物医疗、地质勘探等领域中均有广泛的应用[1-11]。在场景识别[12]、TSP 问题[13]、人脸识别[14]、云计算[15]、计算机视觉[16]等计算机相关领域内亦有广泛应用，特别是在机器学习领域。混合分布模型主要为各类算法的设计提供理论基础，如蜂群算法[17]、人工鱼群算法[18]、免疫算法[19]、蚁群算法[20]和遗传算法[21]等。

在机器学习中，常用的连续型随机变量的混合分布及变型有：指数混合分布及其变型[22]、高斯混合分布及其变型[23]、Gamma 混合分布及其变型[24]、t混合分布及其变型[25]等。对于离散型随机变量的混合分布而言，则通常研究泊松混合分布(或称混合泊松分布)及其在相关领域的应用。冯杭和王胜兵[26]利用 EM 算法求解泊松混合分布模型中的参数向量，并结合算例指出该算法对初值敏感的缺陷，最终引入智能优化算法对算例进行改进。该研究使用泰国北部地区学龄前儿童 1982－1985 年发烧、咳嗽或两者皆有的患病频次作为算例，用 EM 算法通过迭代优化估计出该泊松混合分布的权值(该文称之“权重”)。罗修辉等[27]运用 EM 算法对一种新的系统寿命分布——混合指数-泊松分布进行参数估计，并通过随机模拟，验证了 EM 算法在混合模型参数估计的收敛性和有效性。该研究对象是混合指数-泊松分布，通过 100 个来自指数分布分量的数以及 150 个来自泊松分布分量的数，使用 EM 算法随机模拟出分布的权值。虞欢欢[28]为优化金融管理风险，针对资产组合的相关性结构和组合风险计算的复杂性两方面做出实证研究，用混合泊松分布构建资产组合信用风险模型，利用 85 家上市公司的相关数据估算出泊松混合分布的权值(该文称之为“系数”)，并对模型进行了说明。高迎心等[29]引入了基于变异位点的先验概率分布模型，运用基于混合泊松分布的期望最大化(EM)算法对新生突变识别算法进行改进与优化，研究了有亲缘关系的新生突变的识别，并在识别精度与运算速度方面与已有算法进行对比。该研究结果表明，基于混合泊松分布的期望最大化算法在提高运算速度的同时降低了假阳性比率，具有良好的识别效果。

上述研究均存在一个问题，即混合分布的权值往往依赖于已知或未知的参数，而对未知参数的估计又需要使用经验数据或仿真模拟。由于参数估计方法的不同，造成的估计结果也各有差异，数据的获得往往并非一帆风顺，故这种参数依赖性的问题给混合分布的研究造成了障碍。

为解决混合分布中分量参数依赖性的问题，本文基于多元泊松混合分布的一种变型来进行研究。该混合分布由多元泊松分布经过截断和均化处理后得到伪多元泊松分布，通过集函数矩阵多线性形式的 Pseudo-Boolean 函数矩阵及其相应的Frobenius 范数得到的权值有限混合而成。该多元混合分布的权值在满足有效市场假说，即算术平均合理性的情况下不依赖于任何参数，仅与混合分布中的分量个数有关。

2 研究步骤

多元伪泊松混合分布模型的设计按以下 8 个步骤进行：

(1)设定范式及约束条件；

(2)对多元泊松分布进行截断处理；

(3)在截断处理的基础上，再对其进行均化处理，得到伪多元泊松分布；

(4)定义伪多元泊松混合分布的集函数矩阵；

(5)根据集函数矩阵，写出相应的多线性Pseudo-Boolean 函数矩阵；

(6)根据 Lovász 延拓计算出 Frobenius 范数，构造新的权值；

(7)根据新的权值，写出多元伪泊松混合分布模型的数学表达式；

(8)根据混合分布权值的归一性及非负性，证明其数学表达式正确。

3 分布模型的设计

3.1 范式设定及约束条件

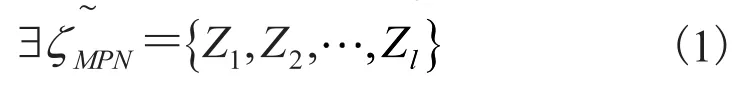
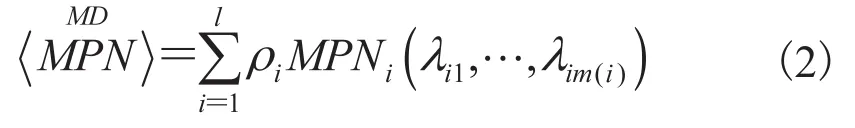
其中，MD为英文 Multivariate Mixture Distribution 的缩写；则称为有限可列的多元泊松混合分布。

(6) 随机变量满足有效市场假说。

3.2 多元泊松分布的截断处理

截断即设定阈值来限制调查对象的范围，超过阈值的对象不做调查，但需将其录入总体分布中，以保证随机分布的完整性。例如，对收入进行调查，小于 5 000 元的用实际收入表示，大于5 000 元不作调查，但需将其作为全部收入分布的一部分，这就是截断。

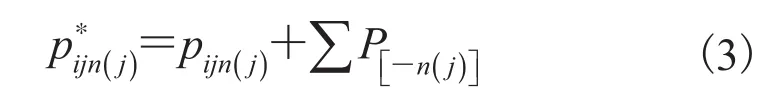
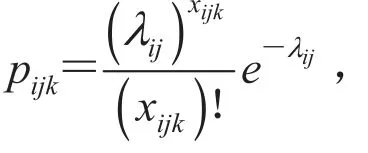
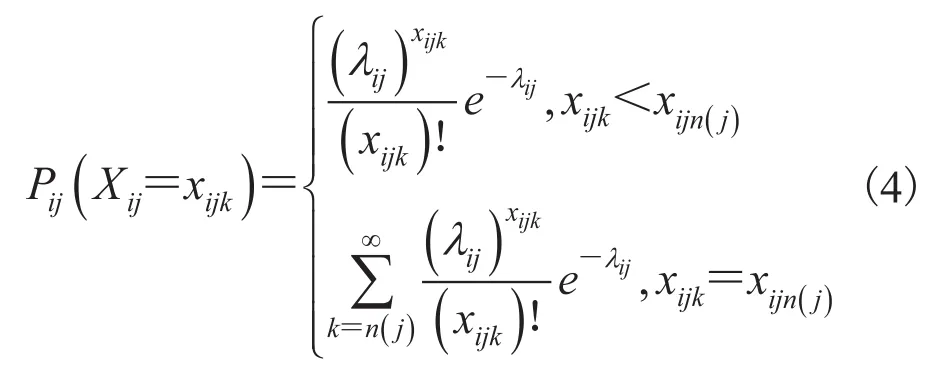
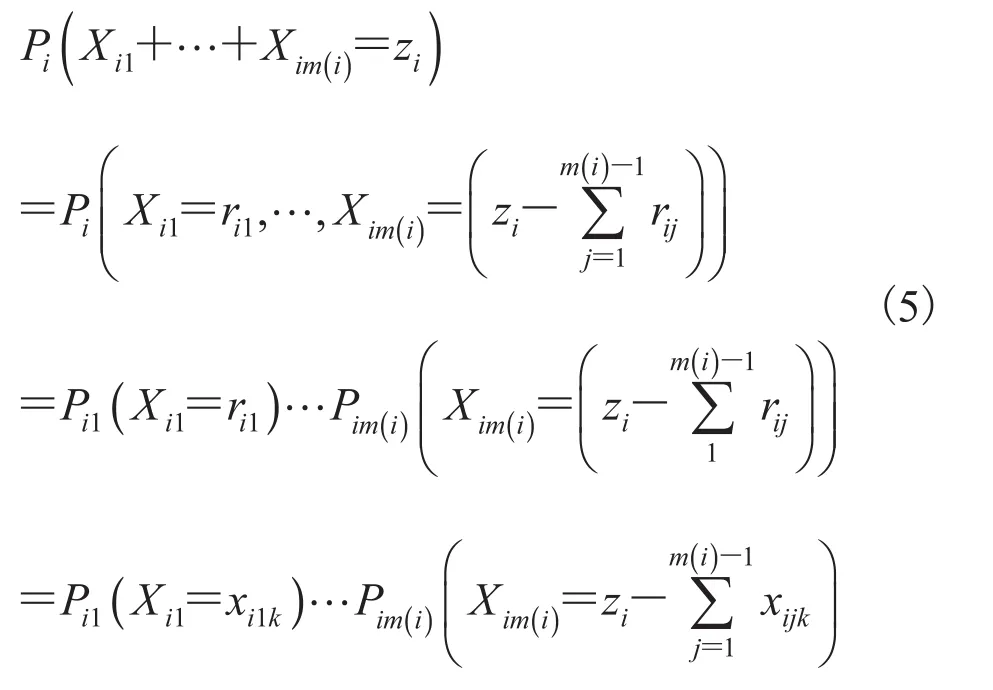
将公式(4)代入公式(5)，可得：

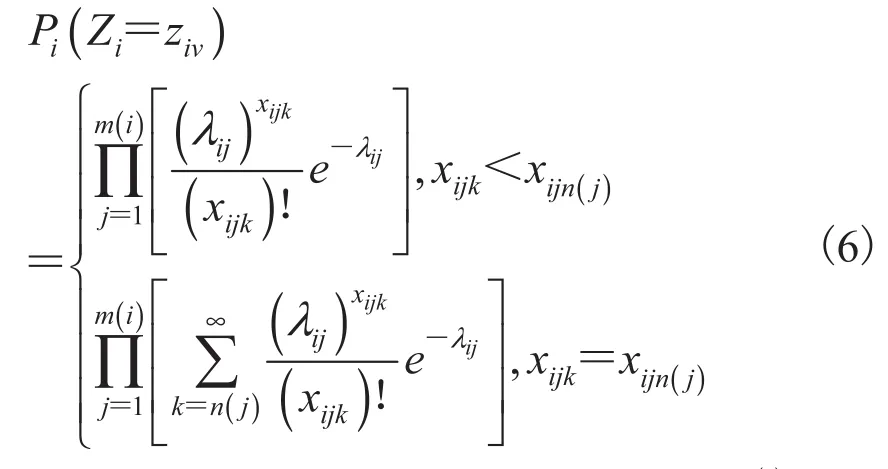
通过截断处理，可将不可数取值的多元离散随机变量ziv的值限定在一个有限域内。但这样的处理会产生一些问题，故对此还需进行均化处理。

3.3 多元泊松分布的均化处理

泊松分布的取值遍布自然数域，即取值有无穷多项，故完成截断处理后的分布在点处有一个相对前个点的概率而言非常巨大的概率值这会造成概率在某一点处的过度堆积，以致于且同时导致为保证随机变量波动的均匀性，须在截断后对其进行均化处理。

均化原本是化学工业上的一个概念，狭义的均化特指通过采用一定的工艺措施，使物料化学成分的波动振幅降低，达到物料化学成分均匀一致的过程。这种方法多用于化工作业的操作中。这里的均化是指广义的均化，特指为了防止离散随机波动过于极端而将极端的概率值进行处理后均匀(算术平均、几何平均等)分散到其余各点的行为。在离散条件下，若有l个极端概率，则舍弃这l个概率值对应的点，将这l个点的概率累积后再进行均化处理。

特别注意，对泊松分布而言，其随机变量取值有无穷多项，从某一项处进行截断处理，显然剩余的项依然是无穷多项，且是单调非减的，则显然可知

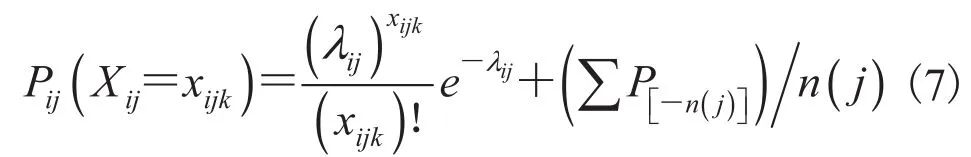
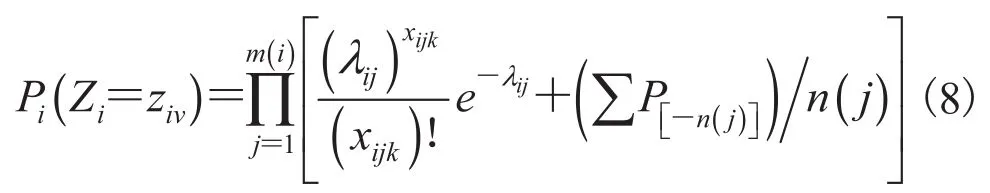
截断处理和均化处理的目的是在原有泊松分布的基础上得到新的分布，即得到新的多元伪泊松分布。为使图中文字公式清晰便于查阅，本文更改一下表示符，设生成多元伪泊松分布的具体操作流程如图 1 所示。

3.4 有限可列的多元伪泊松混合分布

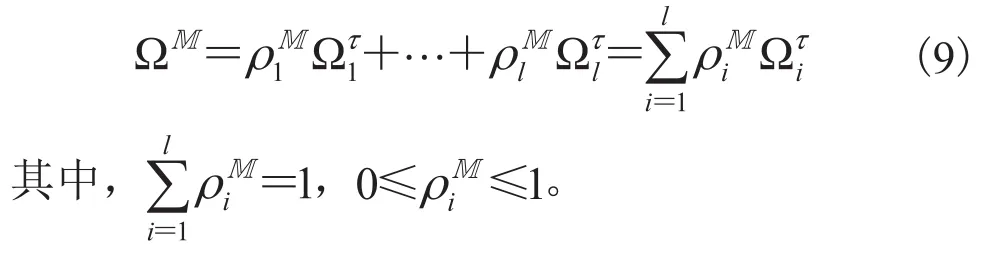
3.5 多元伪泊松分布的集函数矩阵

集函数是计算机技术领域内常用的一类函数，国内外对其也有一定研究[30-35]。离散型随机变量，设的全体取值为则若为的任意子集，则对使得为集函数，设且首先求的集函数。假设空集的集函数继续定义其余子集的集函数，设令：

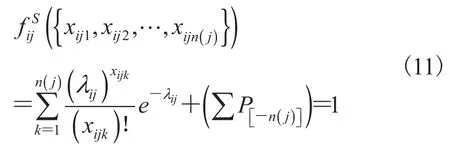
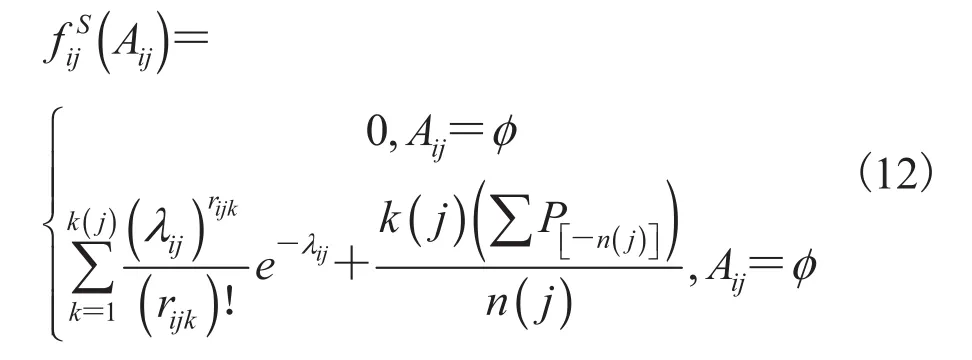
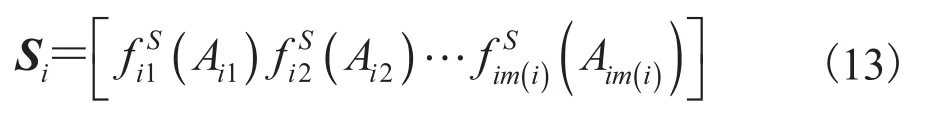
Si为多元随机变量Zi的集函数矩阵。

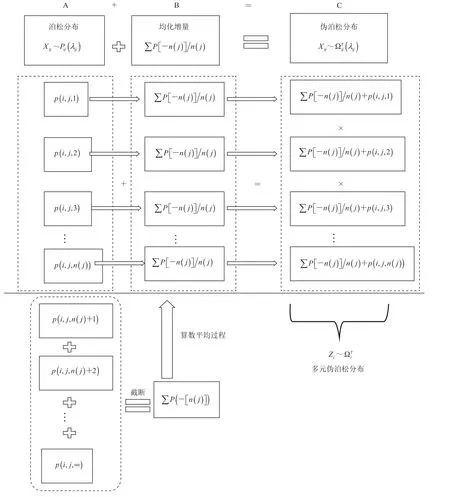
图1 生成多元伪泊松分布的流程图Fig. 1 Flow chart of multivariate pseudo-poisson distribution generating

3.6 多线性 Pseudo-Boolean 函数矩阵

Pseudo-Boolean 函数也是一种计算机技术领域常用的函数[36-38]，其定义域为 0～1 变量且对应到实数域上的函数其中，设则相应的多线性 Pseudo-Boolean函数的表达式为：

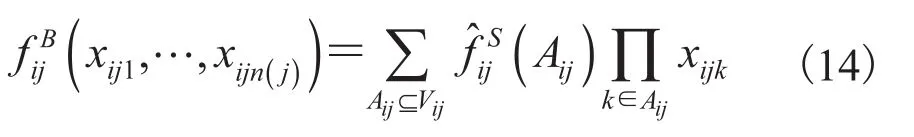
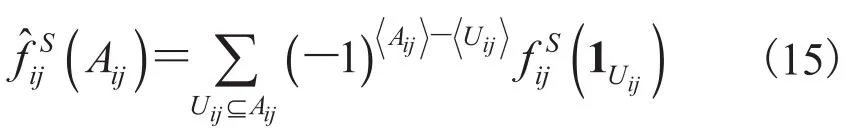
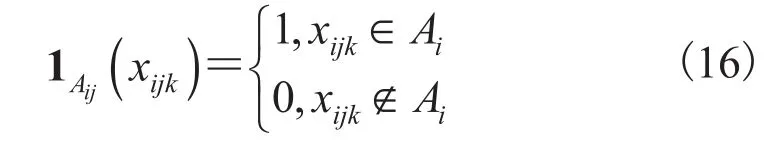
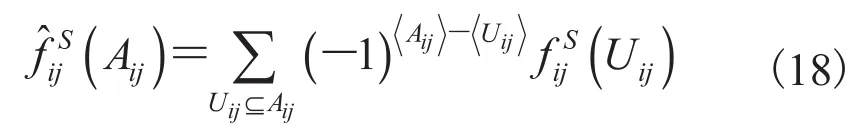
然后将公式(18)代入公式(14)中，可得：

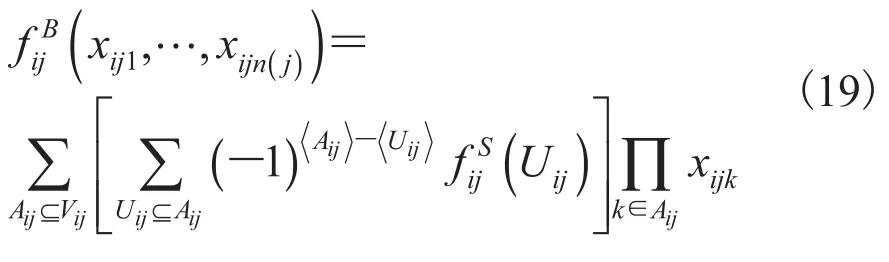
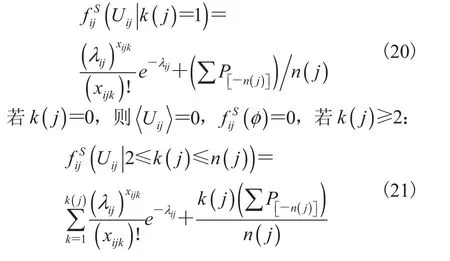
由此可知：

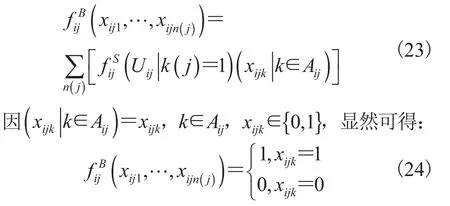
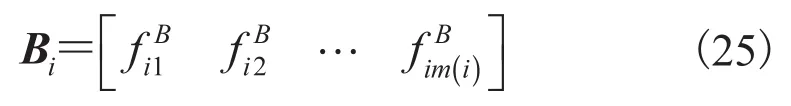
Bi称为多元随机变量Zi的 Pseudo-Boolean 函数矩阵。

3.7 Frobenius 范数

Frobenius 范数作为范数的一种，在计算机领域中有很好的运用[39-43]。运用 Frobenius 范数可得到一个由矩阵中的元素组成的代数式，其定义为：

其中，A为m×n阶矩阵；aij为矩阵中的元素；表示矩阵A的 Frobenius 范数。对于矩阵其 Frobenius 范数的表达式为：

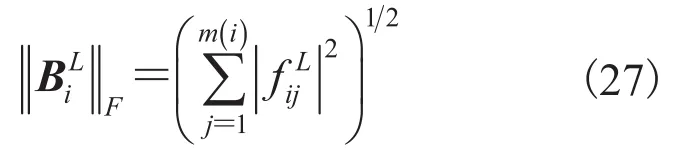
由此可根据 Frobenius 范数来构造多元伪泊松混合分布的权值。

3.8 根据 Frobenius 范数构建的权值

根据公式(27)，可构建由 Frobenius 范数构成的权值，设一共有l个多元伪泊松分布进行混合，则：

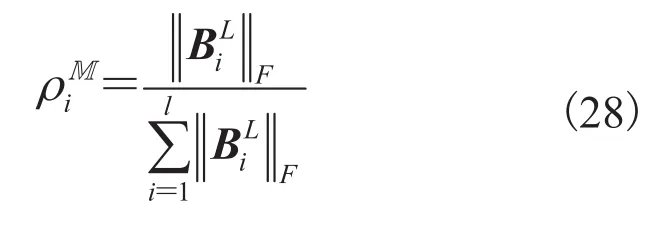
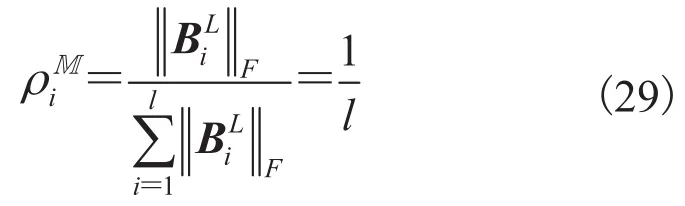
3.9 基于 Frobenius 范数权值的多元伪泊松混合分布模型

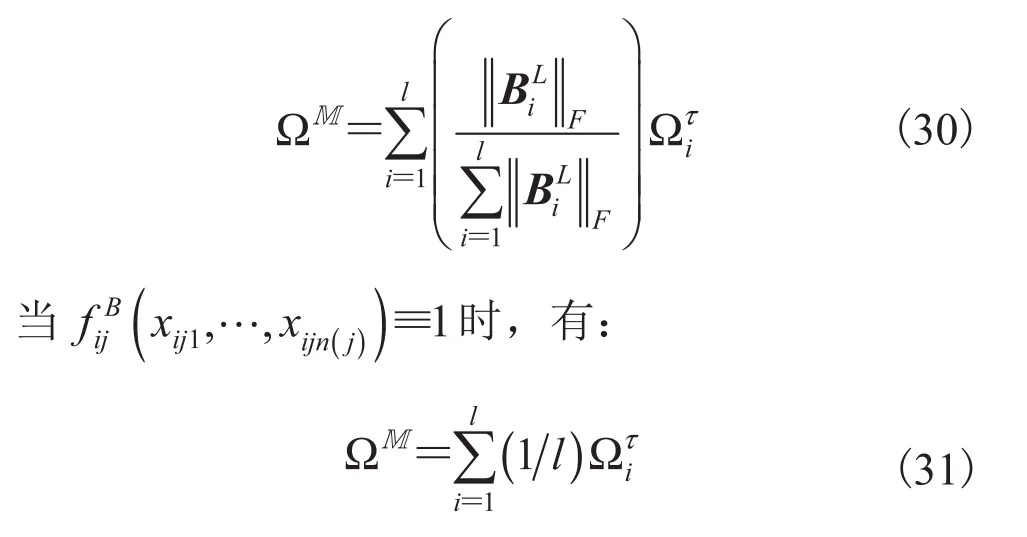
4 仿真实验

模型可用来解决软件工程领域的问题，为突出模型的计算层次以及逻辑推理步骤，本文不会直接令而是根据计算层次来推导得出这一结论。另外由于获取现实数据存在难度，本文通过仿真实验的方式来进行模拟，所有程序均在 R 中完成编辑和运行。

某工业园有A、B、C三家软件研发企业，三家企业均在一年内开发了多款软件，每款软件的开发过程均满足瀑布模型。在开发过程中，每个阶段(可行性研究、需求分析、需要设计、详细设计、编码调试、单元测试、集成测试、确认测试、运行维护、退役)的风险损失次数满足相互独立，且风险损失次数满足，即损失超过 4 次以后就需要进行截断和均化处理，为参数的从第 4 项后开始进行截断和算术均化处理的伪泊松分布。每个企业一年内软件开发过程全部软件的总风险损失次数为为多元伪泊松分布。设三家软件研发企业一年内的混合总风险损失次数满足伪泊松混合分布且假设损失次数满足有效市场假说，求三家软件研发企业的平均总混合风险损失次数，相实验关数据如表1 所示。

使用 R 语言进行程序汇编，按照建模的步骤对基于 Frobenius 范数权值的多元伪泊松混合分布模型编程，然后代入表1 中的数据进行仿真运算，得到结果后将其输出，结果如表2 所示。

由实验结果可知，三家企业一年内总共开发的 377 款软件中，任意一款软件在满足瀑布模型的开发过程中发生的平均总混合风险损失次数为6.562 619 次，显然可知Zmax＝40，Zmix＝0，较小4 分位数表明工业园内三家企业一年内开发的 377 款软件产品的平均质量较好，平均可靠性较高，且混合分布的权值均为 0.333 333 3，满足了有效市场假说，即间接证明了算术平均的合理性。

5 模型比较与优缺点

虞欢欢[28]与本文均以泊松混合分布为基础，且均应用于风险分析领域，但虞欢欢[28]使用混合泊松模型来代替广泛使用的 Copula 模型对资产组合的相关性结构和组合风险计算的复杂性两方面做出实证研究。该研究与本文研究有相近之处，抛开研究目的不同这一点，两者主要有以下几点不同：

(1)权值的构造不同。虞欢欢[28]提出的模型通过结构模型求出债务人历史违约概率来得到混合泊松分布模型的权值。该权值通过历史经验数据求得，而本文是通过多线性 Pseudo-Boolean 函数矩阵的 Frobenius 范数构造混合分布的权值，权值的构造可以使用往期的历史数据，也可以用当期观察数据，构造的方法并不完全依赖于历史经验数据。

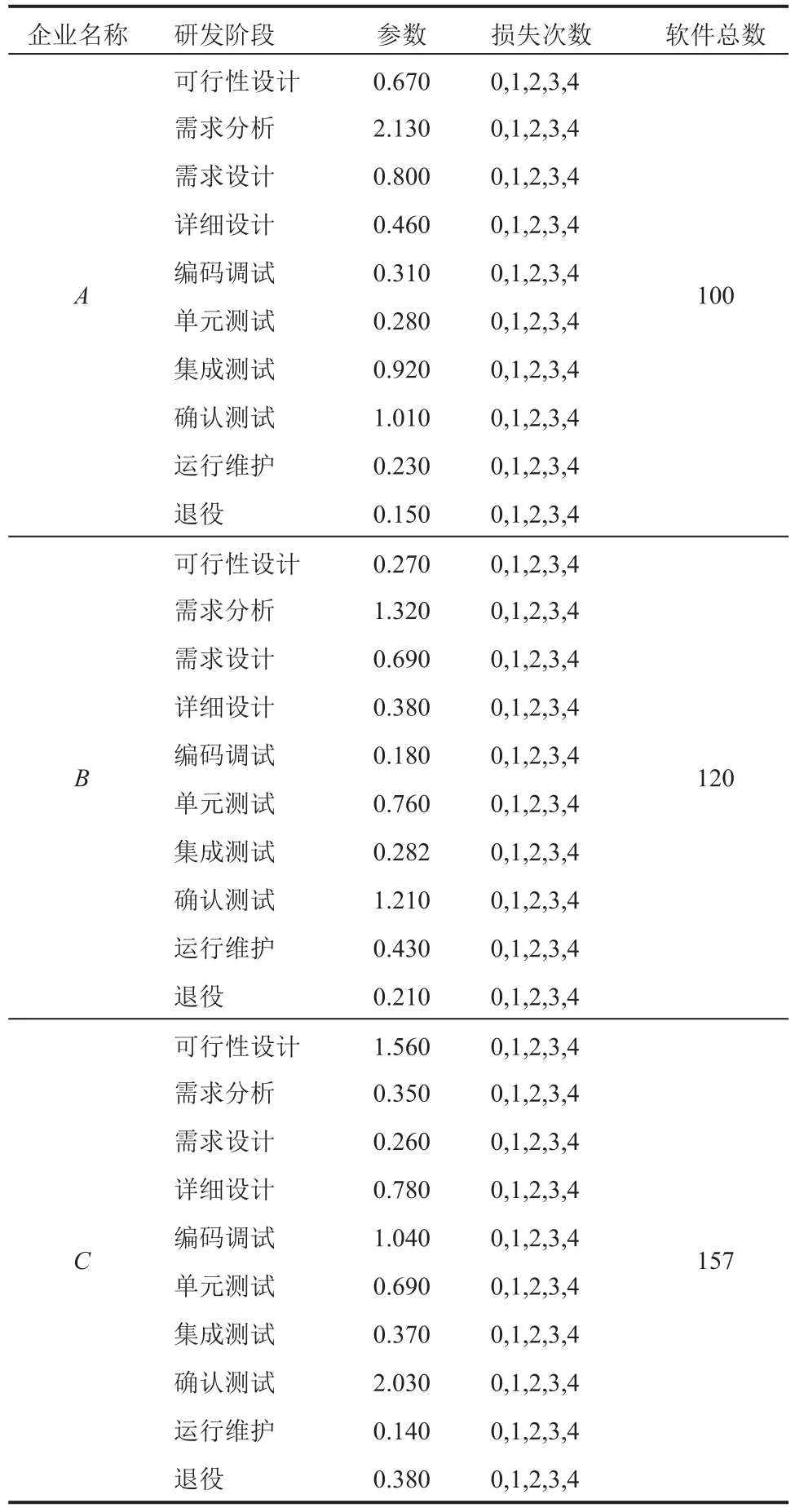
表1 仿真实验的相关数据图Table 1 Data graph of simulation experiment

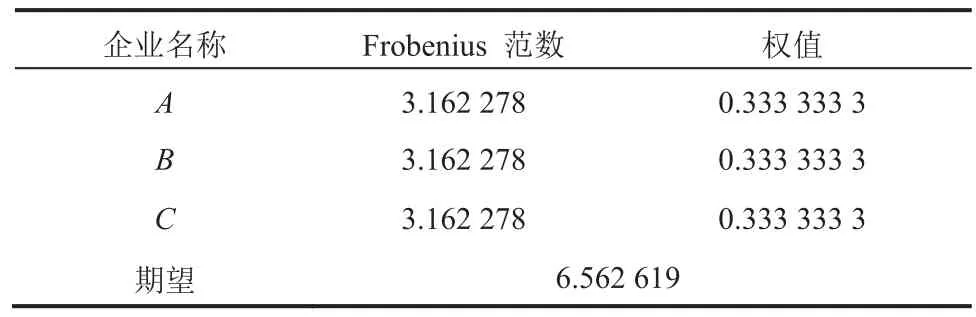
表2 仿真实验运算输出结果Table 2 Output of simulation experiment

(2)模型结构不同。虞欢欢[28]的研究实际是一种风险分析方法，该方法主要包含信用风险结构模型、混合泊松模型两个模型。其中，信用风险结构模型用来构建混合分布模型的权数，因此虞欢欢[28]的研究方法实际上是两个模型，或者可认为是一个组合式模型。而本文自始至终只有一个模型，每一步研究得出的量均是模型的一部分。

(3)研究对象不同。虞欢欢[28]主要针对的是信用资产的风险组合，而本文研究的是一般风险，并没有特殊的约定，仅在仿真实验中使用软件工程中软件开发瀑布模型的风险及风险值对模型进行了实现。

(4)适用度不同。虞欢欢[28]提出的模型更适用于研究信用违约造成的风险，针对性强但普适性稍弱，尤其在缺少违约回收率数据时，使用该模型进行风险分析的精度会受到影响。而本文研究的模型可用于所有风险，只要风险满足或近似满足于多元伪泊松混合分布便可使用模型进行风险分析，但针对性并不强。

(5)模型分量不同。虞欢欢[28]模型的分量均为泊松分布，而本文研究的混合模型中的分量是伪泊松分布，即经过了截断与均化处理的泊松分布。

但是，本文所提模型同样存在不足之处：

①模型的计算复杂度较大，映射关系层层叠加，操作过程中容易产生非系统风险；

②约束条件过多，模型的适用范围由此缩小；

③仅考虑各分布线性有限混合的情况，未考虑无限混合以及非线性情况。

6 总结与未来展望

多元伪泊松分布模型是一种特殊的混合分布模型，它能有效解决复杂的统计计算问题，同时可通过调整混合分布中分布的个数、截断的位置、随机变量的元数等数值型属性，满足不同人群解决不同问题的需求。

未来可继续深入研究这一问题，如将多线性Pseudo-Boolean 函数进行 Lovász 延拓，将定义域从拓展到或者从减少约束条件、模型复杂程度的角度上着手，同时可引入更多专业情景，在符合研究对象所属学科知识的客观条件下对模型进行改良。

[1]曾裕峰, 向修海. 随机波动模型的扩展: 理论与中国股市的实证 [J]. 经济学, 2016, 16(1): 205-228.

[2]肖佳文, 杨政. 混合分布的 VaR 非参数估计: 对期货市场的实证分析 [J]. 系统工程学报, 2016,31(4): 471-480.

[3]肖佳文. 基于混合分布的 VaR 估计及其应用 [D].成都: 电子科技大学, 2015.

[4]张中文. 基于缺失数据的两正态混合分布的参数估计 [D]. 大连: 大连理工大学, 2008.

[5]杨彬. 沪市 A 股交易量与收益率及波动性的关系—基于混合分布模型的实证研究 [J]. 统计与决策, 2005, (8): 91-93.

[6]凌士勤, 杨波, 袁开洪, 等. 基于高频数据的分类信息混合分布 GARCH 模型研究 [J]. 数量经济技术经济研究, 2005, 22(3): 72-77.

[7]杨维维. 贝叶斯模型在老年人健康管理效果评价中的应用 [D]. 南京: 东南大学, 2016.

[8]孙维伟, 陈伟珂. 有限混合分布在车险费率厘定中的应用 [J]. 系统工程, 2016 (5): 144-153.

[9]李程昊. 混合直流输电系统拓扑结构及关键技术研究 [D]. 武汉: 华中科技大学, 2015.

[10]栾途. 透明质酸粘多糖的分子表征、流变学性质及其物理凝胶的研究 [D]. 上海: 上海交通大学,2011.

[11]刘向冲, 侯翠霞, 申维, 等. MML-EM 方法及其在化探数据混合分布中的应用 [J]. 地球科学(中国地质大学学报), 2011, 36(2): 355-359.

[12]胡昭华, 姜啸远, 王珏, 等. 混合深度网络在场景识别技术中的应用 [J]. 小型微型计算机系统,2017, 38(6): 1387-1393.

[13]何广才. 基于云平台的遗传—蚁群混合型算法的研究及在 TSP 中的应用 [D]. 呼和浩特: 内蒙古农业大学, 2016.

[14]周颖. 标记分布在人脸图像属性识别上的应用[D]. 南京: 东南大学, 2016.

[15]降国栋. 基于云计算的计算机辅助诊断及远程诊断平台研究 [D]. 杭州: 杭州电子科技大学, 2016.

[16]张晓庆. 基于计算机视觉的颜色恒常性算法研究[D]. 天津: 天津科技大学, 2016.

[17]赵挺. 蜂群算法及其仿生策略研究 [D]. 杭州: 浙江大学, 2016.

[18]陈新. 基于人工鱼群算法的柔性作业车间调度研究 [D]. 大连: 大连理工大学, 2015.

[19]吴建辉. 混合免疫优化理论与算法及其应用研究[D]. 长沙: 湖南大学, 2013.

[20]黄情操, 余达祥. 单变量边缘分布算法与蚁群算法的混合算法收敛性分析 [J]. 现代电子技术,2012, 35(6): 74-77.

[21]冯巍巍, 魏庆农, 汪世美, 等. 基于混合遗传算法的偏振双向反射分布函数优化建模 [J]. 红外与激光工程, 2008, 37(4): 743-747.

[22]全星澄, 李巍. 基于 EM 算法的有限维混合分布参数估计研究 [J]. 统计与决策, 2017 (12): 25-29.

[23]成英超, 王瑞胡, 胡章平. 一种基于高斯混合模型的协同过滤算法 [J]. 计算机科学, 2017, 44(S1):451-454.

[24]唐绩, 朱峰, 路彬彬, 等. 一种基于混合 Gamma 分布的自动目标识别混合 EM 算法 [J]. 现代雷达,2017, 39(4): 45-49.

[25]李保珠, 董云龙, 李秀友, 等. 基于t分布混合模型的抗差关联算法 [J]. 电子与信息学报, 2017,39(7): 1774-1778.

[26]冯杭, 王胜兵. 有限混合泊松分布参数优化的改进 EM 算法 [J]. 兵工自动化, 2017, 36(1): 80-82.

[27]罗修辉, 韦程东, 王一茸. EM 算法在混合分布模型参数估计中的应用研究 [J]. 广西师范学院学报(自然科学版), 2016, 33(3): 35-39.

[28]虞欢欢. 基于违约强度为混合泊松分布情形的信用资产组合集成风险度量研究 [D]. 杭州: 浙江财经大学, 2015.

[29]高迎心, 温佳威, 徐尔, 等. 基于混合泊松分布的新生突变识别算法 [J]. 中国生物化学与分子生物学报, 2017 (11): 1168-1174.

[30]Wang DW. Fast hybrid level set model for non-homogenous image segmentation solving by algebraic multigrid [J]. Engineering and Technology Research, 2016, doi: 10.12783/dtetr/iceea2016/6727.

[31]Jiang D, Han DF, Hu XL. The shape optimization of the arterial graft design by level set methods[J]. Applied Mathematics: A Journal of Chinese Universities, 2016, 31(2): 205-218.

[32]师肖静, 张兴芳. 概率逻辑、不确定逻辑和模糊逻辑之比较 [J]. 计算机工程与应用, 2017, 53(12):50-52, 69.

[33]钱玲, 张慧, 张化朋. 非可加测度空间上 Egoroff 定理的伪条件 [J]. 模糊系统与数学, 2016 (1): 77-83.

[34]杨勇, 潘伟民, 徐春. 水平集函数规则化的 C-V 主动轮廓模型 [J]. 计算机工程与应用, 2008, 44(34):166-168.

[35]欧阳耀, 李军. Choquet 积分定义的单调集函数的几个遗传性质(英文) [J]. 东南大学学报(英文版),2003, 19(4): 423-426.

[36]李劲, 岳昆, 张德海, 等. 社会网络中影响力传播的鲁棒抑制方法 [J]. 计算机研究与发展, 2016,53(3): 601-610.

[37]Zhao Y, Cheng DZ. Calculus of Pseudo-Boolean functions [C]// Technical Committee on Control Theory of Chinese Association of Automation,Systems Engineering Society of China, 2012.

[38]Marques Silva J. On applying lower bound estimates in Pseudo-Boolean optimization [C]// Proceedings of Guangzhou Symposium on Satis fi ability and Its Applications, 2004.

[39]傅文进, 吴小俊, 董文华, 等. 基于协同表示的子空间聚类 [J]. 模式识别与人工智能, 2017, 30(3):251-259.

[40]吴萱. 基于变分正则化的彩色滤波阵列(CFA)图像去马赛克方法研究 [D]. 南京: 南京理工大学,2016.

[41]张语涵. 鲁棒人脸正面化方法研究 [D]. 南京: 南京理工大学, 2016.

[42]石聪聪. 矩阵 Frobenius 范数不等式及次可加性研究 [D]. 重庆: 重庆大学, 2016.

[43]翁小清, 沈钧毅. 基于滑动窗口的多变量时间序列异常数据的挖掘 [J]. 计算机工程, 2007, 33(12):102-104.

[44]Mankiw GN. 经济学原理: 宏观经济学分册第 7版 [M]. 北京: 北京大学出版社, 2012.