中国生产性服务业发展的影响因素分析——基于贝叶斯模型平均(BMA)方法的实证研究

张 超，郑长娟

(宁波大红鹰学院金融贸易学院，浙江宁波 315175)

一、引言及文献综述

生产性服务业(Producer Services)被Mabry等[1]最先提及，之后经众多学者的深化发展，对其内涵已达成一致，即为其他产品或服务生产提供中间投入的服务行业，它是一种服务形式的生产资料[2]。在2016年我国政府工作报告中，“服务业”被先后提到14次，出现频率远远超过城镇化、小康社会、改革开放、创业创新等热门经济学词汇，可见，在十三五时期我国经济社会发展战略中，服务业占有关键的战略地位，在供给侧结构改革过程中，特别是生产性服务业，已经发挥和将要起到极为重要的促进作用[3]。从20世纪80年代至今，我国服务业也取得了较快发展，服务业产值占同期GDP的份额由1978年的23.9%增至2016年的51.6%，服务业已占据我国经济总量的半壁江山，成为我国第一大产业，服务业俨然已成为我国经济发展的“稳定器”和“助推器”。作为现代服务业的关键构成要素，生产性服务业发展已经牵涉我国产业结构的转型升级，它将成为我国经济发展新动能[4]。现阶段众多发达国家服务业已达4个“70%”水准，对比中国，生产性服务业却仅占GDP的15%-20%，未及发达国家二分之一。不难发现，纵然近几年中国生产性服务业得到快速增长，但较西方国家仍差距甚大，生产性服务业发展薄弱，俨然已成为我国经济转型升级的“短板”。伴随着信息化加速推进，影响其发展的因素显现出多而复杂的趋势，科学辨别主导影响因素以及知晓这些因素影响如何，这对于补齐我国生产性服务业发展“短板”和加快经济转型升级起到关键作用。

生产性服务业是全世界产业竞争的战略制高点，它的迅速突起受到了国内外不少研究者的关注，众多研究者对影响其发展的因素进行了探讨。Solo[5]提出生产性服务业由制造业规模和业务范畴扩张而产生的一种需求，其发展受制造业的影响；Illeris[6]和方慧[7]的研究表明人力资本的加入是保障生产性服务业得以生存的关键；Francois[8]实证得出西方发达国家经济状况以及它们产业结构都会影响生产性服务业；Stare[9]实证研究促进斯洛文尼亚生产性服务业发展的因子，结果发现交通设备、通信设施、人力资本、市场化程度等均产生了显著影响。Micucci等[10]规模报酬递增的特点出发，分析得到生产性服务业增长与产业集聚间存在紧密联系。韩德超等[11]、刘纯彬等[12]、毕斗斗等[13]利用省际面板数据，经实证发现专业化程度、服务效率、政府规模、信息技术、城市化水平等与生产性服务业发展呈正向关系；胡国平等[14]、盛龙等[15]使用中国城市面板数据分析表明对外开放度、经济发展水平、制造业集聚、人力资本、地方保护等都会产生明显作用；翁春颖[16]依据浙江省时间序列数据研究得出经济发展状况、市场化程度、对外开放度、技术进步对生产性服务业作用明显，工业化发展对其影响不显著；万千欢等[17]基于广州市时间序列数据，研究发现政府作用与工业发展水平是关键影响要素；余得生等[18]采用江西省时间序列数据，实证得出政府宏观调控与市场机制对生产性服务业增长起正向效应。

国内外学术界对生产性服务业发展的影响因素做了大量实证研究，并得到了一些富有价值的成果。然而，从这些研究成果不难看出，若研究的方法不一样或者选择的变量不全面时，不同学者的研究得出了不一致甚至对立的结果，可见现有的研究仍然存在一些不足。总体来说，存在以下两方面的局限:(1)影响因素考虑不全面。影响生产性服务业发展的因素众多，但现有的研究大多数都是将重心置于一个或几个解释变量上，综合考虑各个因素的研究较少。(2)没有考虑模型的不确定性。由于经济系统的开放性和复杂性，影响因素相当多元，研究者无法确定应该将哪些指标作为解释变量，意味着研究者们在构建回归模型时忽视了模型的不确定性。而BMA方法在解决以上两个问题上具有较强优势:第一，尽管神经网络分析等模型也可以对大样本影响因素进行重要性识别，但它们不能确定影响因素的作用方向[19]，因此，考虑到本文的研究目的，BMA方法较为适合。第二，Raftery等[20]、Fernandez等[21]通过研究证明贝叶斯模型平均(BMA)方法可以解决模型不确定性问题，且由于BMA方法在处理模型不确定性问题上的优越表现被广泛用于诸多领域，国外学者主要将该方法用来研究通货膨胀、经济增长、教育回报、能源估算的影响因素等多个领域[22-26]，而少数的国内学者也将该方法用于研究我国经济增长、通货膨胀、房地产价格的影响因素等领域[27-29]，但国内鲜有人将BMA方法运用于生产性服务业影响因素研究中。

基于此，本文摒弃人为事先设定模型及变量的传统，引入模型的不确定性，采用贝叶斯模型平均(BMA)方法对所有可能影响我国生产性服务业发展的因素依据其重要性进行分类和排序，以此确定主导影响因素，并探讨经济新常态下加快生产性服务业发展的政策性建议。

二、模型、方法和数据

(一)模型设定和估计方法

1.单一模型设定

本文采用Moral-Benito[30]和Cuaresma等[31]的方式，且根据研究目标，将单一模型设置为个体固定效应模型，如下:

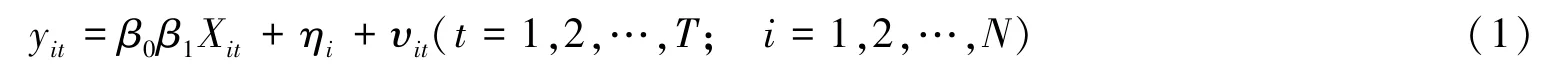
其中，yit表示i地区在t期的生产性服务业发展水平，以生产性服务业增加值比重表示；β1表示待估系数向量；Xit表示影响生产性服务业发展的因素；ηi表示不可观测的地区固定效应；υit表示独立同分布的随机误差项。使用上述面板模型能够有效地避免因遗漏重要解释变量而产生的偏差。

令M＝{M1，M2，…，MN}，即所有潜在解释变量经随意组合后构造的模型空间，若解释变量共有K个，因为解释变量的任意一种组合均会构成单一模型，故而模型空间M中共包括N＝2K个模型。依据2K个模型的估计结果，再利用BMA方法能够求得各个解释变量的后验概率及其系数的相关统计指标。具体计算如下。

Mj是模型空间M中第j个模型，p(Mj)为模型Mj的先验概率，利用贝叶斯理论，计算得到模型Mj的后验概率为:

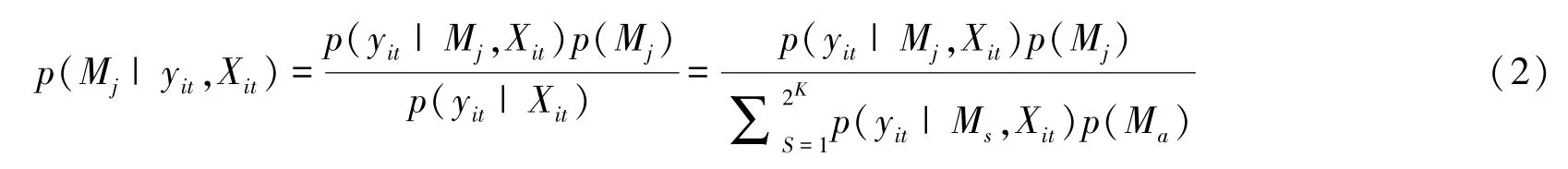
其中，p(yit｜Ms，Xit)＝ʃp(yit｜β1j，Mj，Xit)p(β1j｜Mt，Xit)dβ1j为Mj的边际似然值，p(yit｜β1j，Mj，Xit) 为Mj对应的似然函数，p(β1j｜Mt，Xit)为Mj中参数向量β1的先验概率分布。

将模型后验概率当作权重，使用加权平均便可算出参数向量β1的后验概率、均值以及方差为:

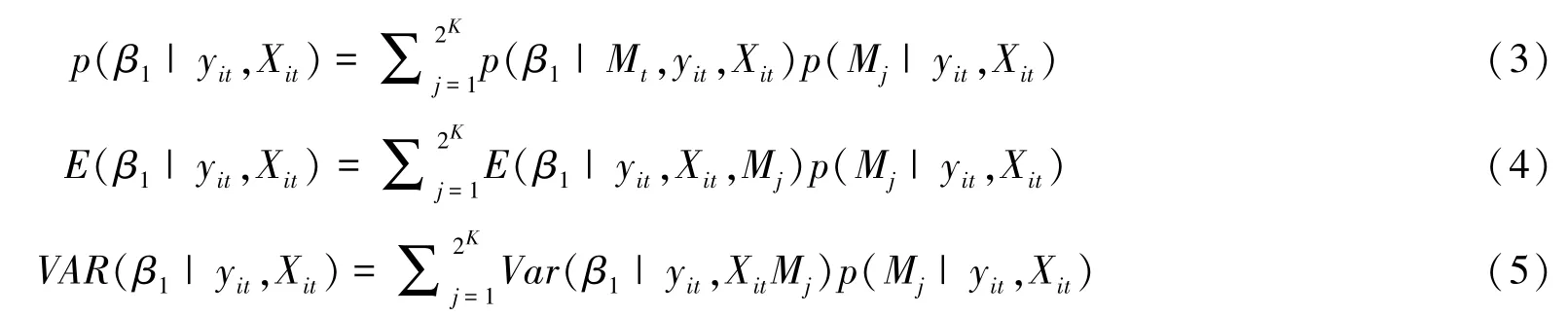
其中，p(β1｜Mj，yit，Xit) 表示在Mj条件下参数β1的后验概率，p(Mj｜yit，Xit) 为Mj后验概率，E(β1｜yit，Xit，Mj)与Var(β1｜yit，XitMj)为单一模型中参数向量的后验均值及方差。

2.参数和模型先验概率设定

使用BMA方法处理模型不确定性问题必须设置先验分布，且要求设置两个先验分布。其一，设定参数β1的先验分布:George等[32]认为把扩散单位信息先验分布(Diffused Unit Information Prior，简称DUIP)当作一类标准先验分布拥有很好的安全性和稳定性，因此本文将参数先验分布设定为“DUIP”。其二，设定模型的先验分布:此设定是彰显模型不确定性的重要环节。一个具有2K个单位的模型空间，往往设置所有模型都服从均匀先验分布，即:

(6)式说明增加(减去)某一变量的先验概率为1/2，即预先对变量和模型的选取没有偏向性，因而在先验信息匮乏的情况之下，均匀分布是模型先验分布的标准分布。

3.估计方法

在参数和模型的先验概率设定完成后，就可通过(2)～(5)式采取迭代的方法来计算参数和模型的后验概率。经George等[32]证实，当自变量数量较多时，采取迭代的方式计算后验概率的工作量非常之重。为了减轻计算工作量，本文将借鉴Madigan等[33]提出的马尔科夫蒙特卡罗模型综合(MC3)抽样技术对模型空间予以抽样，通过公式(2)～(5)对新样本进行迭代计算参数和模型的近似后验概率。MC3算法倾向于抽取较高后验概率的模型，当抽样数达到一定数量时，能够确保抽样结果收敛于迭代结果。

MC3抽样技术以指定的概率分布对模型空间M＝{M1，M2，…，MN}进行抽样获取备选模型M∗，然后以指定的概率接纳该备选模型。在第s次抽签中，倘若备选模型被接纳，则M∗＝M(S)，反之，则接纳上一次抽样模型，即M∗＝M(S-1)。第s次抽样备选模型存在如下三种选择:(1)前一次抽样模型M(S-1)，(2)基于M(S-1)去除一个变量的模型，(3)基于M(S-1)中添加一个变量的模型。最终会以下述概率确定备选模型:

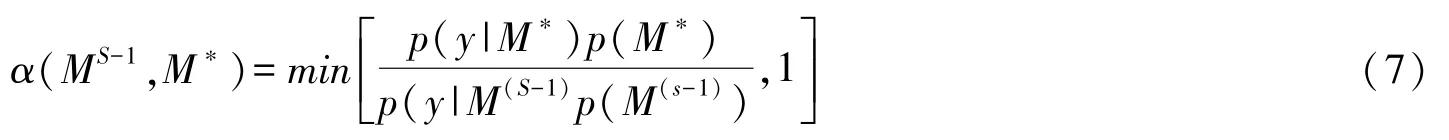
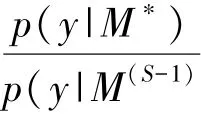
(二)数据来源及变量选取

本文采用中国2004-2015年30个省市自治区的面板数据，由于西藏资料缺失较多，故没有将其列入样本。本研究数据出自于对应年份的《中国统计年鉴》与中经网统计数据库。本研究所涉及的具体变量说明如下。

1.被解释变量选取

现有对生产性服务业发展的实证研究中，学者们往往选取增加值比重、就业比重、产业密度等指标，本文参照韩德超等[11]的做法，用生产性服务业增加值比重作为生产性服务业发展水平代理变量(由于我国省级统计口径和分类标准的不一样，无法获取狭义行业的相关数据，因此，本研究将使用广义行业的数据进行分析，即第三产业增加值扣除房地产业、住宿餐饮业等明显为消费性服务业的行业增加值)。

2.解释变量选取

在解释变量选取方面，本文综合文献[20][21][30][31]等的做法，参照两项准则(其一，所选取的变量皆是近年来在实证研究领域中经常出现，且被认为能够产生影响的解释变量；其二，所选取解释变量的数据具备较好的可得性)，选取了5个层面的16个变量，其中需求性因素有经济发展水平、专业化程度、工业化程度、制造业集聚度；供给性因素有物质资本投入、人力资本投入、劳动力投入、技术进步、服务效率；制度因素有市场化程度、对外开放度、政府宏观调控；其他外部性因素有城市化水平、人口老龄化、基础设施水平、产业融合程度。此16个解释变量基本上代表了中国生产性服务业发展的热门影响因素。具体指标描述详见表1，为了剔除异方差和量纲的干扰，本文对全部指标均作对数化处理。

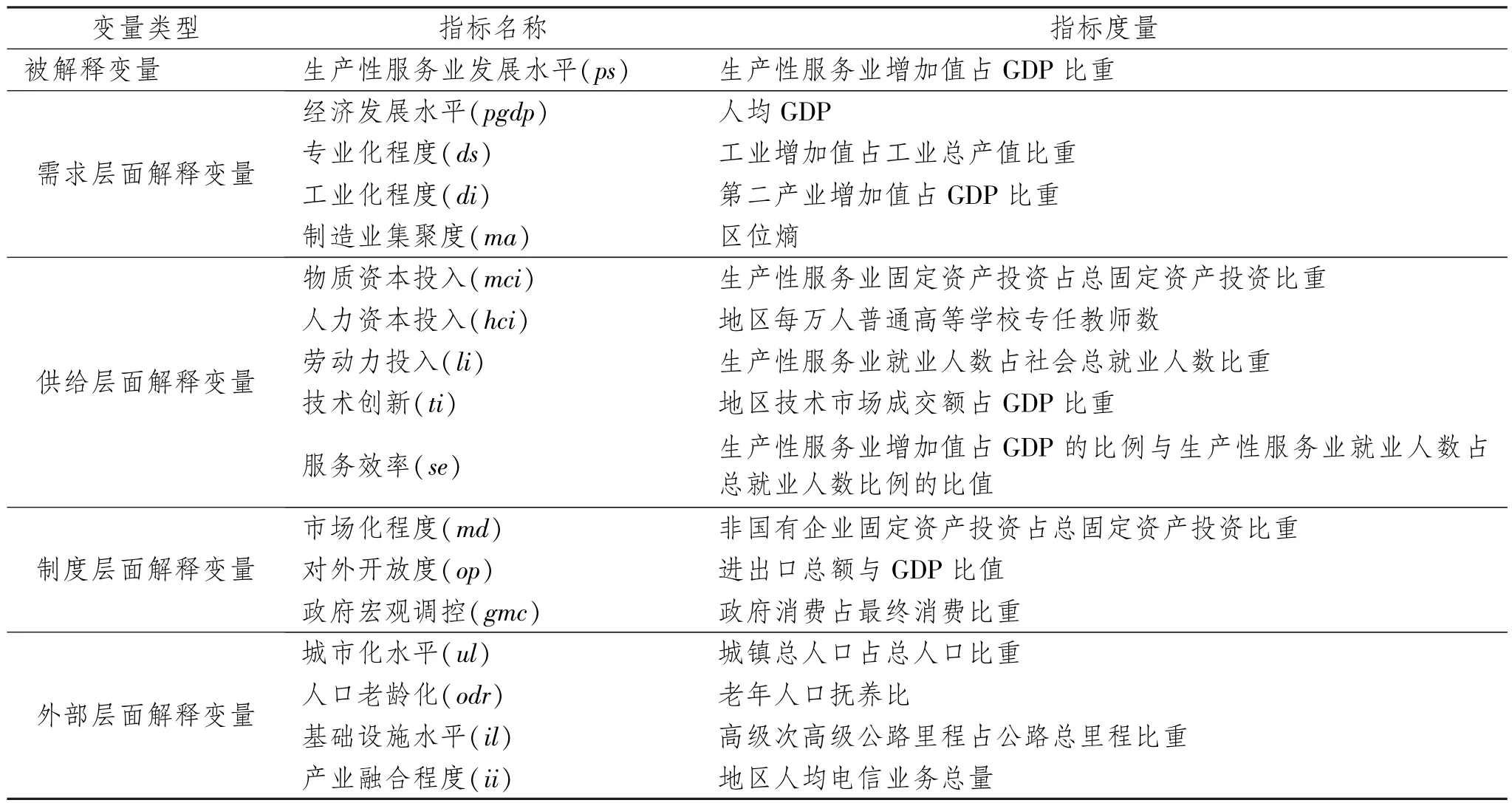
表1 指标描述

二、估计结果分析及有效性检验

在个体固定效应模型设定下，16个解释变量生成的备选模型共有216个，文章采取MC3抽样技术抽取所有模型中的65 500个。将前500次抽样当作预热实验，再将最后的65 000次抽样作为模拟样本。

(一)估计结果分析

本文使用R-3.1.1软件，调用BMS软件包，对模型进行估计。图1展示了生产性服务业后验模型规模分布均值图，不难看出模型先验概率的确为均匀分布，符合前文的先验假设；模型后验概率在横坐标取8.813 7处到达极大值，也就是后验模型规模分布均值为8.813 7，这意味着在抽到的65 000个模型中，所有单一模型平均约包含9个解释变量。

表2为贝叶斯模型平均估计结果。其中，第三列为后验概率，由公式(3)得到，表示影响因素的解释能力，且16个变量按照后验概率从小至大排列；第四列是后验均值，由公式(4)得到，其符号代表影响因子的作用方向；第五列为后验标准差，对公式(5)计算结果开方得来；第六列表征符号确定率，它表示出现某解释变量的全部模型回归结果当中，此变量的系数符号与后验均值符号相同的可能性，用来说明变量的稳健性。

图1 后验模型规模分布均值

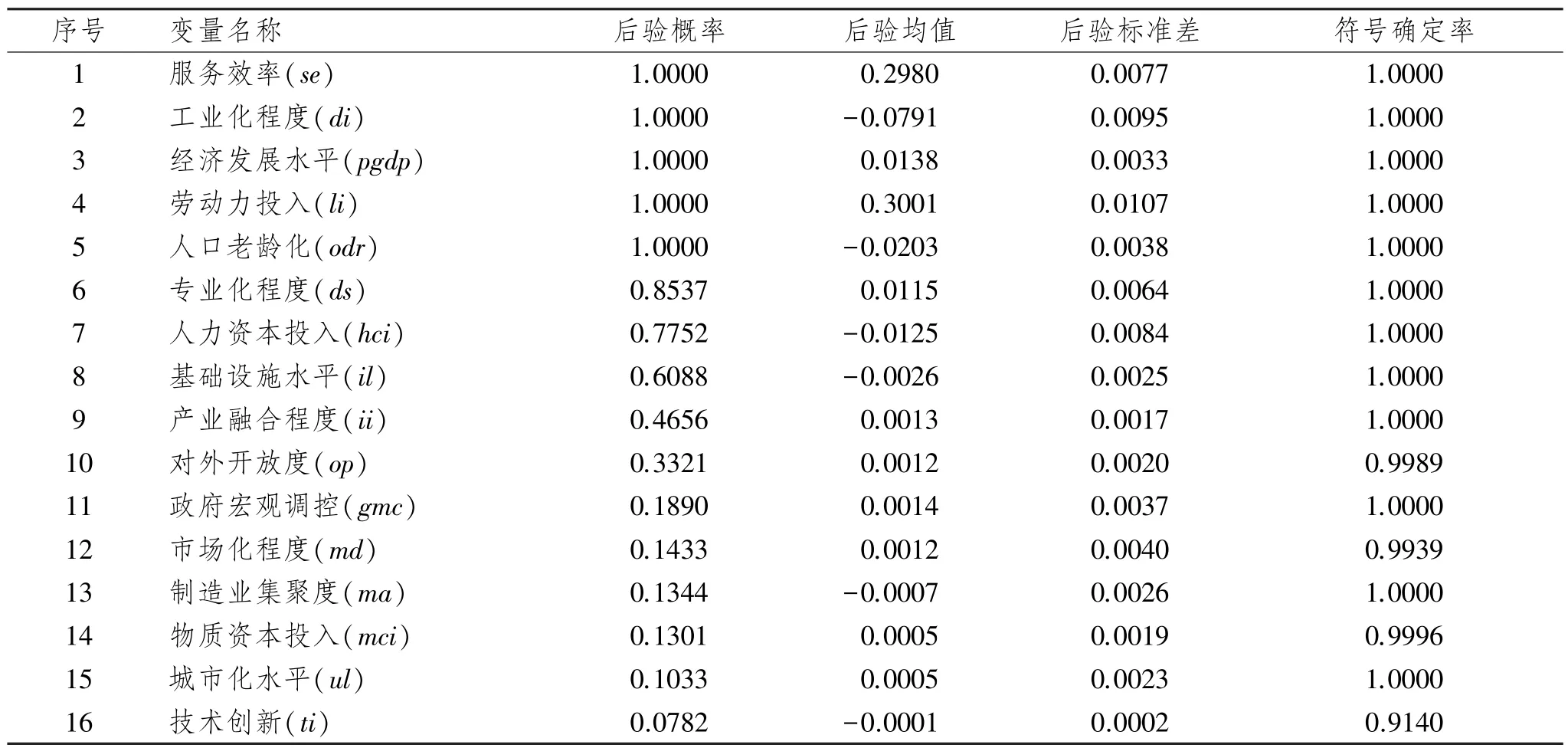
表2 解释变量BMA估计结果

根据表2的估计结果可以看出，服务效率、工业化程度、经济发展水平、劳动力投入以及人口老龄化5个变量的后验概率都达到1.000 0，意味着它们的解释能力最强，是最为重要的解释变量；专业化程度、人力资本投入以及基础设施水平3个变量的后验概率大于0.5且小于0.9，表明它们也具有较好的解释能力，但与服务效率等5个解释变量相比重要性稍弱一些；产业融合程度、对外开放度、政府宏观调控、市场化程度、制造业集聚度、物质资本投入以及城市化水平等7个变量的后验概率都是介于0.1与0.5之间，说明它们可以对生产性服务业发展进行一定的解释，但与产业融合程度等3个解释变量相比重要性又稍弱一些；技术创新变量后验概率不足0.1，表明它的解释力度最弱，除非有充分的理论依据或较为强烈的主观意念，不然不会将其引入模型当中。此外，观察表2容易发现所有变量的符号确定率都高于90%，表明这些变量的稳健性都非常好，意味着本文的基本结论是稳健的。

由此可见，服务效率、工业化程度、经济发展水平、劳动力投入以及人口老龄化这5个变量的后验概率均为1，远远高于其他变量，它们是我国生产性服务业发展最为密切的影响因子，具体解释如下。

服务效率对生产性服务业的影响为正，可能的解释为:第一，从行业关联面来看，服务效率提升减少了向下游企业供应中间服务的成本，强化了企业自身的竞争力，牢固了生产性服务业的市场基础，进而促进其增长；第二，从生产性服务业本身来看，服务效率的提升能够减少运营成本，直接导致盈利增加，使自身积累增多，进而会扩大投入力度，驱动自身发展。因此，务必要将提升服务业经济效率作为新时期中国经济转型升级的关键内容。

工业化程度对生产性服务业的影响为负，可能的解释为:现阶段我国服务业发展存在要素配置扭曲现象，一般制造业供给严重过剩与对生产性服务业的投资匮乏问题并存，体现为“总需求向服务业集中而总供给向制造业倾斜”的结构性矛盾，即在资源固定前提下，工业化发展所要求的资源投入霸占了生产性服务业发展所要求的资源投入，因挤出效应的干扰，现阶段我国工业化进程一定程度上阻碍了生产性服务业的发展。

经济发展水平对生产性服务业的影响为正，可能的解释为:经济水平是生产性服务业得以发展的有力支撑，经济水平越高，对生产性服务业的需求量更大、生产性服务业的供给能力更强，对应着生产性服务业发展状况会更好。目前全国各个省份都在积极适应经济稳增长的新常态，集中精力发展生产性服务业，不断推进产业结构调整升级。

劳动力投入对生产性服务业的影响为正，可能的解释为:劳动力对于所有行业来说，都是一个关键的投入要素，特别是对于服务业，劳动力的投入直接影响行业的规模。某一行业的劳动力数量愈庞大，其创造出的价值愈高，对于具备很强劳动力就业吸纳能力的生产性服务业格外如此。

人口老龄化对生产性服务业的影响为负，可能的解释为:基于供给层面，我国人口老龄化呈持续增长态势，导致人口红利逐渐消失，人口老龄化会改变了劳动力资源禀赋，致使劳动力短缺和成本上升，劳动力供给减少限制了生产性服务业的发展；基于需求层面，人口老龄化对生活性服务业特别是与相关的老年服务业的需求较大，像个人和家庭服务、健康照料和医疗服务、政府和社会公共部门提供的服务，而对生产性服务业的需求较少，因此，人口老龄化最终会妨碍生产性服务业发展。

(二)模型有效性检验

下文将从犯错率与参数显著性两个角度验证BMA方法在处理模型不确定性问题时发挥的作用。

1.基于模型犯错率的视角

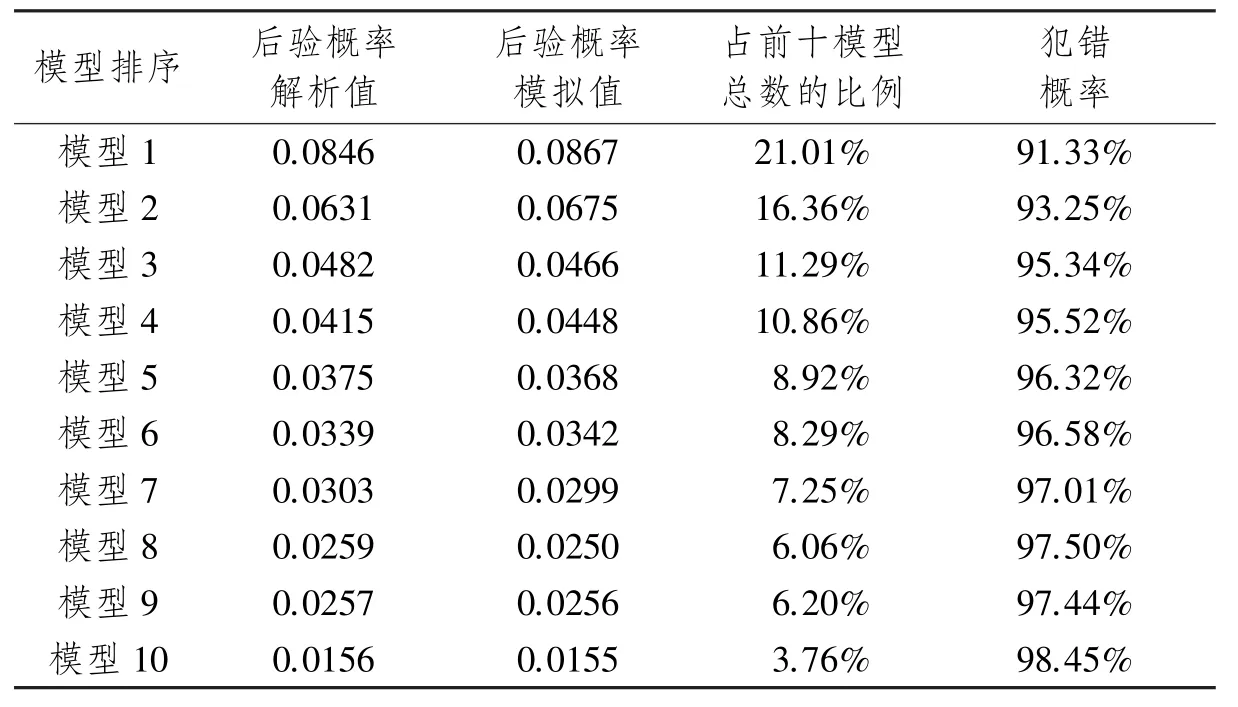
表3 排名前十的单一模型BMA后验概率

表3给出了后验概率排在前面的十个单一模型，且按照后验概率从大到小排列。第二列数据由公式(2)算得，第三列数据由单一模型被抽样次数占总抽样次数比重获得。由表3不难看出，后验概率解析值与MC3模拟值非常靠近，这说明MC3抽样结果收敛于迭代结果，意味着MC3方法是一个有效的抽样技术。此次抽样65 000次，占模型总数216的99.18%。由第四列可以看出，单一模型的后验概率呈发散分布，后验概率位列第一的模型1占总数比重的21.01%，排名前四的模型共占59.52%，排名第十的模型比重仅为3.76%，这说明利用MC3进行抽样时，模型链并没有在任何模型上停留太多时间。观察第五列，发现倘若把后验概率最高的模型1当作“真实模型”来进行实证研究，将导致犯错率达到91.33%，倘若把后验概率最低的模型10当作“真实模型”，犯错率则会更高，这表明单一模型在解释生产性服务业上存在严重的模型不确定问题，另一方面这也证明采用BMA方法解决模型不确定性的必要性。

2.基于参数显著性的视角

对BMA方法与单一模型参数显著性进行比照，同样能够判定单一模型的不确定性。表4给出了BMA方法与两个单一模型的对比回归结果。“BMA模型结果”选自于表2；单一最优模型为后验概率值最高的模型，且含有8个解释变量；根据图1，单一模型解释变量数均值为9，选取表2中后验概率最高的9个解释变量组成九变量模型。由于本文设定所有单一模型为个体固定效应模型，因此两个单一模型都使用固定效应模型进行估计，计算得到系数均值与标准差。

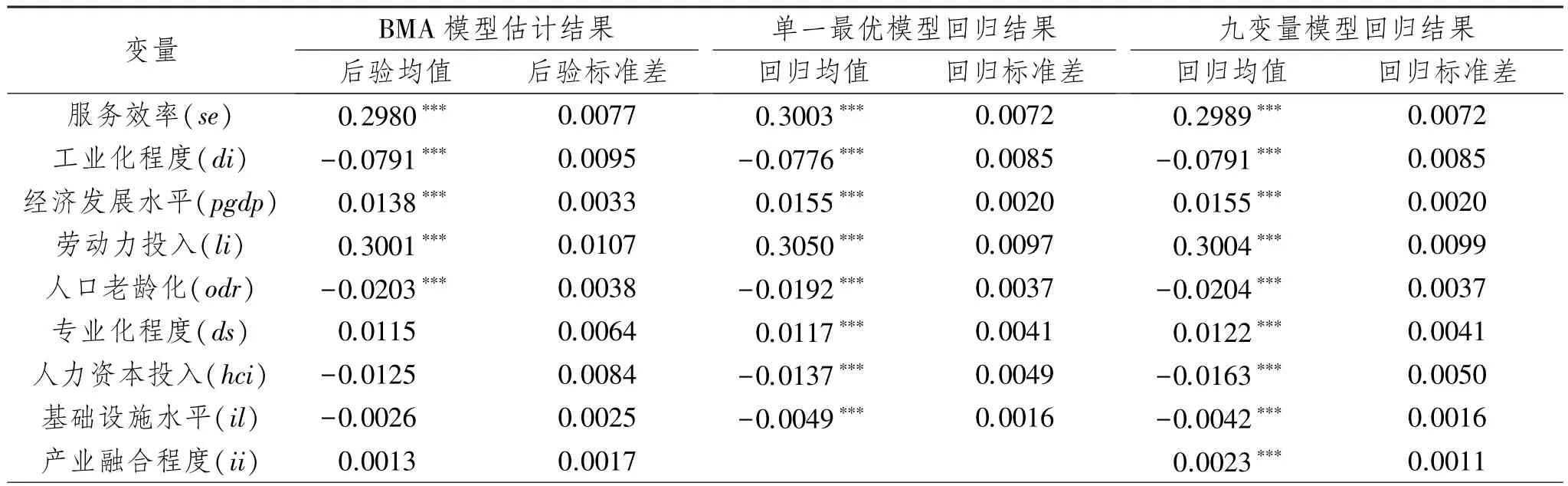
表4 BMA模型与单一模型回归结果比较

表4可以证明BMA方法的重要性。对于解释变量基础设施水平，它的BMA后验均值及标准差为0.002 26与0.002 5，单一最优模型结果为0.004 9和0.001 6，十变量模型结果为0.004 2和0.001 6。不难发现，两个单一模型参数回归均值均大于BMA方法下的均值，但回归标准差却小于BMA方法下的标准差。由此发现，某变量在单一模型中统计显著，但在BMA模型中却不具有显著性。因此，在假定单一模型正确的条件下对某些参数显著性做出的判断，在BMA方法中几乎都是不成立的。因此，所有解释变量对生产性服务业发展的解释能力不能由单一模型算得的统计量所决定，而应由BMA方法计算的后验均值与标准差来判定。对表4中其余变量同样能够得到相似的结论。

三、主要结论及政策启示

本研究采用贝叶斯模型平均方法，基于模型不确定性视角，对影响我国生产性服务业发展的众多因素的有效性及稳健性予以识别和检验，估计结果显示:在可能对我国生产性服务业发展产生影响的16个指标中，服务效率、工业化程度、经济发展水平、劳动力投入以及人口老龄化等5个变量的后验概率均达到1，意味着上述5个解释变量具有极强的解释能力，与我国生产性服务业发展的关系最为密切。其次，专业化程度、人力资本投入以及基础设施水平等3个解释变量的后验概率大于0.5且小于0.9，表明它们也具有一定的解释能力，但重要性程度弱于前5个解释变量。最后，余下的8个解释变量的后验概率都低于0.5，表明它们解释能力较差。这些结果在一定程度上包容并验证了现有众多国内学者采用单一模型所得到的不同甚至相反的研究结论。此外，本研究还基于犯错率和参数显著性两个角度验证了BMA方法确实具备处理模型不确定性的作用。

“十三五”期间，大力发展现代服务业，尤其是发展生产性服务业是我国迈入全面小康社会和开启基本实现现代化新进程的重要举措之一。因此，基于研究结论，本文就经济新常态下如何加快发展生产性服务业提出以下政策取向性建议:

第一，积极提升生产性服务业经济效率。在提高经济效率方面，不仅仅只重视工业制造业层面，还需多关注生产性服务业层面。首先，与生产性服务业结构调整、现代化改造以及体制机制改革等结合起来，统筹规划，切实促进生产性服务业演变成新的经济增长极和可持续增长动能；其次，与工业强国、工业强省联系起来，真正使它们得到有机互促，如抓工业一样，政府应建构并完善工作推进机制，定制和施行针对性规划、生成年度评价体系以及考核机制；最后，与政府经济管理理念与办法改进同步起来，继续降低市场准入体制，让市场主体的能动力与创造力得以更大程度释放。

第二，努力解决生产性服务业结构性矛盾。我国生产性服务业发展过程中存在严重的要素配置扭曲问题，一般制造业供给严重过剩与对生产性服务业的投资不足短板并存。为此，政府应把滥用在僵尸企业、过剩产能中的实物资源、信贷资源和市场空间，利用供给侧结构改革、剿灭僵尸企业、去除过剩产能的实际行动，渐渐市场化地迁移至生产性服务业。

第三，适时进行“简政放权”等制度改革。生产性服务业供给侧改革过程中，离不了制度改革。对生产性服务业适时实施“简政放权”“减税降负”等政策，有助于其健康可持续发展。生产性服务业是人力、知识和技术资本集聚行业，具有轻资产、“折旧”快等特征，致使其实际税负已重于制造业。除了做到简政放权、减少审批周期，还需完善财税、土地政策、拓宽融资渠道，督促有关部门加快制定配套措施，为生产性服务业营造良好发展环境。

第四，挖掘人口第二次红利，倒逼劳动力素质提升。随着中国老年人口比例的不断提高和刘易斯转折点的到来，人口红利渐渐消失。面对人口老龄化给生产性服务业部门带来的挑战与机遇，第一应驻足未来，密切关注我国人口老龄化带来的庞大服务需要，加快增强相关老年服务业供给质量；第二应努力学习美国等西方国家应付人口老龄化的成功经验，正视挖掘人口第二次红利，提升劳动者素质和效率，补全劳动力不足短板，持续推进生产性服务业供给迈向依托知识、技术和人力资本驱动的新阶段。

[1]MABRY F，JAMES J.The Production and Distribution of Knowledge In the United States.[M].Princeton:Princeton University Press，1962.

[2]DALY D J，GRUBEL H G，WALKER M A.Service Industry Growth:Causes and Effects[J].Canadian Public Policy，1990，16(1):114.

[3]刘志彪.现代服务业发展与供给侧结构改革[J].南京社会科学，2016(5):10-15.

[4]徐冠巨.生产性服务业是我国经济发展新动能[EB/OL].(2016-03-11)[2017-04-28].http://news.xinhuanet.com/politics/2016lh/2016-03/11/c-128792925.htm.

[5]SOLO R A.Manufacturing Matters:The Myth of the Postindustrial Economy[J].California Management Review，1989，29(3):9-26.

[6]ILLERIS S.Producer Services:the Key Sector for Future Economic Development?[J].Entrepreneurship ＆ Regional Development，1989，1(3):267-274.

[7]方慧.中国承接服务业国际转移的经济效应研究[M].北京:中国人民大学出版社，2015.

[8]FRANCOIS J F.Producer Services，Scale，and the Division of Labor[J].Oxford Economic Papers，1990，42(4):715-729.

[9]STARE M.Determinants of Producer Services Development in Slovenia[J].Eastern European Economics，1999，37(6):54-70.

[10]MICUCCI G，GIACINTO V D.The Producer Service Sector in Italy:Long-term Growth and Its Local Determinants[J].Spatial Economic Analysis，2009，4(4):391-425.

[11]韩德超，张建华.中国生产性服务业发展的影响因素研究[J].管理科学，2008(6):81-87.

[12]刘纯彬，杨仁发.中国生产性服务业发展的影响因素研究——基于地区和行业面板数据的分析[J].山西财经大学学报，2013(4):30-37.

[13]毕斗斗，方远平，JOHN B，等.中国生产性服务业发展水平的时空差异及其影响因素——基于省域的空间计量分析[J].经济地理，2015(8):104-113.

[14]胡国平，李广新，张丽.我国大城市生产性服务业内部扩散研究:基于行业差异性的视角[J].宏观经济研究，2012(12):74-79.

[15]盛龙，陆根尧.中国生产性服务业集聚及其影响因素研究——基于行业和地区层面的分析[J].南开经济研究，2013(5):115-129.

[16]翁春颖.浙江生产性服务业发展影响因素的实证研究[J].企业经济，2013(4):123-126.

[17]万千欢，千庆兰，陈颖彪.广州市生产性服务业影响因素研究[J].经济地理，2014(1):89-93.

[18]余得生，刘俊.欠发达地区生产性服务业发展的影响因素研究——以江西省为例[J].企业经济，2017(1):135-141.

[19]尹海洁，高云红.神经网络分析与相关分析、回归分析的比较——基于大学毕业生的成就性水平及其影响因素的研究[J].江苏社会科学，2014(6):24-31.

[20]RAFTERY A E，MADIGAN D，HOETING J A.Bayesian Model Averaging for Linear Regression Models[J].Journal of the American Statistical Association，1997，92(437):179-191.

[21]FERNANDEZ C，LEY E，STEEL M.Benchmark Priors for Bayesian Model Averaging[J].Journal of Econometrics，1998，100(2):381-427.

[22]COGLEY T，SARGENT T J.The Conquest of US Inflation:Learning and Robustness to Model Uncertainty[J].Review of Economic Dynamics，2005，8(2):528-563.

[23]KOOP G，KOROBILIS D.Forecasting Inflation Using Dynamic Model Averaging[J].International Economic Review，2012，53(3):867-886.

[24]LEY E，STEEL M F J.On the Effect of Prior Assumptions in Bayesian Model Averaging with Applications to Growth Regression[J].Journal of Applied Econometrics，2009，24(4):651-674.

[25]LEY E，STEEL M F J.Mixtures of G-priors for Bayesian Model Averaging with Economic Applications[J].Journal of Econometrics，2012，171(2):251-266.

[26]CULKA M.Applying Bayesian Model Averaging for Uncertainty Estimation of Input Data in Energy Modelling[J].Energy，Sustainability and Society，2014，4(1):1-17.

[27]王亮，刘金全.中国经济增长的决定因素分析——基于贝叶斯模型平均(BMA)方法的实证研究[J].统计与信息论坛，2010(9):3-7.

[28]陈伟，牛霖琳.基于贝叶斯模型平均(BMA)方法的中国通货膨胀的建模及预测[J].金融研究，2013(11):15-27.

[29]卢二坡，张超.基于贝叶斯模型平均(BMA)方法的中国房地产价格影响因素分析[J].长安大学学报(社会科学版)，2016(4):68-76.

[30]MORAL-BENITO E.Determinants of Economic Growth:a Bayesian Panel Data Approach[J].Review of Economics and Statistics，2012，94(2):566-579.

[31]CUARESMA J C，DOPPELHOFER G，FELDKIRCHER M.The Determinants of Economic Growth in European Regions[J].Regional Studies，2014，48(1):44-67.

[32]GEORGE E I，MCCULLOCH R E.Approaches for Bayesian Variable Selection[J].Statistica Sinica，1997，7(2):339-373.

[33]MADIGAN D，YORK J，ALLARD D.Bayesian Graphical Models for Discrete Data[J].International Statistical Review，1999，63(2):215-232.