加权填充与兴趣相融合的相似度改进算法

黄迪　吴静

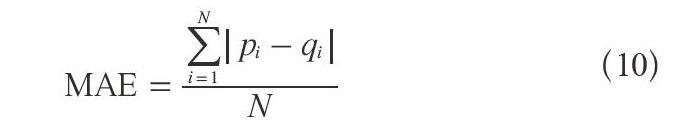
摘 要：针对传统协同过滤推荐算法在面临用户评分矩阵极端稀疏而导致推荐结果不佳的问题，文中提出了一种改进的协同过滤推荐算法。该算法的相似度值由用户评分相似度值和用户兴趣相似度值组成，其中用户兴趣相似度用来拟补单独填充值导致用户个性化不足的问题。用户评分相似度值采用混合加权填充值对用户评分矩阵进行填充，即在原用户评分矩阵上采用由用户评分矩阵行和列的平均数、众数、中位数等混合加权拟合成的最终值对未评分项目进行填充，加权值的权重取决于这三种值单独填充的实验结果。首先将加权填充后的矩阵作为伪矩阵，在伪矩阵上进行相似度计算。然后通过用户兴趣相似度值建立用户兴趣矩阵，拟采用用户对项目属性评价的次数来衡量用户对不同项目属性的偏好度，利用相似度计算公式计算用户间的兴趣相似度值。最后对Movielens电影数据集进行仿真实验。实验结果表明，相比传统的协同过滤推荐算法，改进的评分矩阵混和加权填充与用户兴趣相结合的协同过滤推荐算法不仅有效缓解了数据稀疏问题的影响，同时也提高了推荐精度。

关键词：推荐系统；相似度融合；协同过滤；混合加权填充 ；稀疏性；兴趣

中图分类号：TP391 文献标识码：A 文章编号：2095-1302（2018）03-00-04

0 引 言

电子商务和社交网络的快速发展，极大地改变了人们的生活方式，但同时网络用户量每年呈指数级的增长也造就了信息量的急速增长和膨胀，出现了“信息过载”现象[1]。为解决这一问题，多种方法已被提出。众所周知，信息检索技术需要手动输入关键字，虽在一定程度上节约了大量时间，但该技术需要用户明确查找的信息。而网络信息量的增大，导致检索的信息亦数量巨大，因此该项技术也面临着越来越严峻的挑战：如果无法准确给出检索内容，那么查找目标内容就比较困难。推荐技术依赖于对用户以往数据的分析，同时参考用户的喜好和行为习惯[2]，可主动为用户推荐，相当于智能推荐。然而个性化的推荐技术依赖于用户的行为信息，推荐精度也取决于用户所遗留信息轨迹的多寡。现有推荐算法主要面对的是数据稀疏性[2]、冷启动 [3，4]以及可扩展性问题。

当前各种改进算法层出不穷。李颖[5]等人利用稀疏的用户项目评分矩阵，分析近邻用户组与推荐精度间的关系，提出一种基于双重阈值近邻查找的协同过滤算法；Sarwar[6]等人提出SVD分解技术降低稀疏矩阵的维数，提高了项目或用户间的相似度，在一定程度上提高了推荐精度，但需注意，降维技术会损失部分信息；于世华[7]等人提出用户-项目类别评分和用户-项目类别兴趣相似度融合的算法，提高了推荐精度，该算法对合适权值的选取会直接影响用户的最终相似度值，影响推荐的质量；黄创光[8]等提出不确定近邻因子来预测评分产生推荐；陈宗言等人[9]提出一种基于项目特征属性的稀疏数据预处理方法来提高推荐精度，该方法只对数据预处理进行了改进，并未对协同过滤算法进行改进，因此有待进一步研究。

本文在上述研究的基础上，提出一种改进的协同过滤推荐算法。该算法首先在解决数据稀疏的问题上充分考虑了填充值对推荐质量的影响，采用加权填充的方式，缓解矩阵的稀疏性。在预测精度上，充分利用用户个性化的兴趣信息，将融入的伪矩阵和兴趣矩阵相似度值作为最终相似度值，最后把得到的相似度值在原矩阵上进行评分预测，采用Top-N算法筛选，利用平均绝对误差值来衡量算法的优劣。

1 混合加权填充方法和用户喜好矩阵的建立

1.1 协同过滤推荐算法介绍

表1所列是一个用户-项目评分矩阵R={rij}m×n。该评分矩阵中的m代表用户数目，n代表项目数目。元素rij代表用户i对项目j的评分，空缺值代表该项目没有被评分。一般的协同过滤推荐算法主要分析用户-项目矩阵，预测未评分项目值，向目标用户推荐，基于用户的协同过滤算法计算目标用户与所有用户的相似度值，找出最为相似的用户集，选择对目标项目评过分且相似度最大的前k个用户作为目标用户的邻居集。通过评分预测公式计算出未评分项目评分。

常用的相似度计算方法包括余弦相似性[10]、Pearson相关相似性以及修正的余弦相似性[10]。这里采用Pearson相关相似性进行计算。

Pearson相关相似性公式如下：

1.2 各项填充值的计算以及混合加权方法

可采用填充值的办法解决矩阵稀疏的問题。考虑到单独值的填充过于单一且不具有代表性，则采用三种值混合填充，这里采用每行和每列的平均值、众数值以及中位数值混合，这三个值分别用Fa，Fp，Fm表示。

（假设用户u没有对项目v评过分，Iu表示已被用户u评过分的项目，而Uv表示已被评过分的用户集合）

（1）评分矩阵行和列的平均值计算

（4）混合加权值计算

过于单一的值不具有代表性，相比单独值，混合所有值考虑到了三种值的所有情况，更具说服力。在用户-项目评分矩阵中将评分矩阵计算的三种值[11]（平均值，众数，中位数）全部分配一定的权值（权值都小于1），即α，β，χ且α+β+χ=1，各种权值的大小取决于单独填充实验的准确度。

混和加权填充值的计算公式如下：

1.3 用户喜好相似度的概述

单独的矩阵填充能够缓解数据的稀疏性，但填充值并未考虑到用户的兴趣，无法体现个性化用户的偏好程度。因此，为拟补填充值缓解用户数据稀疏带来的用户个性化问题的不足，引入了用户-项目属性的兴趣相似度。可以通过统计用户评价的项目属性次数之和来定义用户-项目兴趣的程度。例如，一个人看过很多电影（一部电影包含不止一个属性），如果想对这个人看过的爱情属性的电影进行统计，那么就可以从评价过的电影中包含爱情属性的次数来衡量这个人对爱情电影的偏好程度，次数越高代表兴趣程度越大。建立一个兴趣矩阵sm×k，用以表示用户对各项目属性的感兴趣程度。

其中：Cuv表示用户u和用户v评价过的所有项目属性的集合，tu，c表示用户u评价的项目包含属性c的总次数，tv，c表示用户v评价过的项目包含属性c的总次数，和分别表示用户u和用户v评价所有项目属性次数的平均值。

2 改进的协同过滤推荐算法

2.1 相似度融合

由 （1）式可知用户评分的相似性，用户评分相似度用simR（u，v）表示，而用户对项目属性偏好相似度用（8）式的simI（u，v）表示，将这两种相似度融合得到最终相似度sim（u，v），这里引入一个权重参数w，。

sim（u，v）=wsimI（u，v）+（1-w）simR（u，v） （9）

2.2 混合加权填充和用户兴趣相结合的协同过滤推荐算法流程

输入用户评分信息，项目评分矩阵R={rij}m×n，项目属性矩阵sm×k，邻居数目k，输出目标用户的预测评分。算法简要的步骤如下：

（1）通过扫描用户评分矩阵R={rij}m×n，计算行和列的平均值、众数、中位数等值，依次添加到空缺值部分，形成对应的伪矩阵。

（2）在形成的伪矩阵上利用式（1）计算与目标用户的相似度值，根据设定邻居数目k选出各邻居集合。

（3）利用评分预测式（2）在原矩阵上预测根据设定的k个邻居用户预测目标用户评分，根据MAE比较各项填充实验的精度大小。

（4）根据步骤（3）得到的实验结果，分配三种值的权重，利用式（6）计算得到混合加权值，再重复步骤（2）得到用户评分相似度值和邻居集。

（5）扫描项目属性矩阵sm×k，利用式（8）计算用户间的偏好相似度值。

（6）融合步骤（4）和步骤（5）计算的相似度值（融合参数实验部分包括如何选取）。

（7）重复步骤（3）得到预测评分以及MAE值。

3 实验结果与分析

3.1 实验所用的数据集

采用著名的Movielens数据集[12]进行实验，该数据集可以在线获得，它提供了用户信息表、电影信息表和评分信息表。用户信息表包含用户的年龄、国籍、性别等，评分信息表包括943位用户、1 682部电影以及100 000条评分，评分范围为1～5分，電影信息表包含电影的发布时间以及电影类型等。每个用户至少对20部电影有过评分。我们用x表示该数据集稀疏程度：x=1-100 000/（943×1 682）=0.936 9。将数据集随机分为训练集和测试集，比例为4∶1。训练集用来进行算法实验与预测估算，测试集用来比对预测估算的结果。

3.2 实验评估标准

本实验为验证混合加权填充值，结合用户喜好的改进算法的推荐效率比未填充以及单独填充的传统协同过滤推荐效率高，采用平均绝对误差（MAE）衡量其推荐精度。这种衡量推荐精度的办法比较容易理解，其实质是计算预测值和真实值之间的平均偏差。用pi表示预测值，qi表示真实值，那么MAE的表达式如下：

平均绝对误差值越小，推荐的结果就越准确，推荐算法性能就越好。

3.3 实验结果

3.3.1 混合加权填充值α，β，χ的确定

为确定混合加权填充值权值关系的大小，可分别进行单独的填充实验，即平均数、众数、中位数填充实验。为保证实验的准确性，可采用多次实验得到的MAE计算平均值（即5-交叉测试方法）。邻居集的大小从5增加到40，比较三种填充值实验得出的推荐精度的大小关系，精度越好给它的混合权重就越大。实验采用Person相关相似性在各填充后的伪矩阵上计算相似度，评分预测在原矩阵上进行。实验结果如图1所示。

观察图1可知，平均数、众数、中位数作为填充值会生成不同的伪矩阵，并以伪矩阵作为信息矩阵，计算各用户的相似度，然后，在原矩阵上进行评分预测。实验结果表明，相比较传统的协同过滤算法，三种填充实验均有效改善了推荐精度，并且可知，选择中位数填充得到的推荐精度依次好于众数和平均数填充。因此，对于混合加权填充权重的大小关系有χ>β>α>0，且，这三种填充值均满足式（6）条件。

3.3.2 相似度融合参数ω的确定

式（9）中的相似度参数ω会直接影响最终相似度值的大小，即最终的推荐质量。为确保融合参数的可靠性，将数据集按1∶4的比例随机分成两组不同的测试集和训练集，分别用D1和D2表示。分别在D1和D2数据集上进行仿真实验，将最近邻居用户数k设为15，25，35，参数ω的步长设为0.1，，实验同样采用5-交叉测试方法，取5次测试实验的平均值作为最后结果。D1数据集上MAE的仿真结果如图2所示，D2数据集上MAE的仿真结果如图3所示。

从图2和图3 可知，不同的用户邻居集影响最终的平均绝对误差，当实验中邻居集中的用户个数为35时，相比邻居用户个数为15或25的情况，可取得较精确的推荐结果。同时从两组图中可以观察到，当相似度融合因子为0.3时，推荐系统的MAE取得最小值，表明最合适的相似度融合参数为0.3。因此对于式（9），在用户总的相似度计算过程中，用户评分相似度所占的权重为0.7，用户兴趣相似度权重为0.3。

3.3.3 填充值和用户兴趣相结合实验结果

从图2和图3的实验结果可知混合加权填充值之间的关系，即χ>β>α>0，用户评分相似度和用户兴趣相似度融合参数为w=0.3。因此，实验随机选取满足条件的混合加权值权重即可，这里取中位数权重为0.5，众数权重为0.3，平均数权重为0.2，将得到的混合加权填充值与用户兴趣相似度相结合进行实验，并与传统的协同过滤算法实验进行比较，实验结果如图4、图5所示。

由图4和图5的实验结果可知，混和加权填充原始矩阵与用户兴趣相结合的算法比传统的基于Pearson相关相似性的协同过滤推荐算法推荐精度有明显改善。说明混合加权填充和用户兴趣相结合的推荐算法在改善了数据稀疏性的情况下，更近一步提高了推荐质量。

4 结 语

本文主要针对传统的协同过滤推荐中数据稀疏问题进行了研究。考虑到数据稀疏问题的解决一般都采用填充数值的办法，而过于单一的数值不具有代表性，且忽略了用户的个性化兴趣。因此，本文从数据稀疏和用户个性化兴趣两方面入手，在缓解用户项目数据稀疏性方面采用混合加权填充值的办法丰富了填充值的多样性，其中，混合加权值权重依赖于各项填充值单独实验的预测效果。为进一步提高用户间相似度计算的精度，引入了用户兴趣模型，将用户评分相似度和用户兴趣相似度通过单独的实验找到合适的拟合参数，得到最终的相似度值，经实验验证了该方法的可靠性。未来将进行如何在合理的加权值中找到最优权值与用户兴趣受多种因素影响的研究。

参考文献

[1]刘鲁，任晓丽.推荐系统研究进展及展望[J].信息系统学报，2008，4（1）：82-90

[2]吴杰，冯峰.综合用户偏好和优先新品推荐的协同过滤推荐算法[J].计算机应用与软件，2014，10（31）：285-287.

[3] MOSHFEGHI Y，PIWOWARSKI B，JOSE JM.Handing data sparsity in collaborative filtering using emotion and semantic based features[C].In proceeding of the 34th international ACM SIGIR conference on research and development in information retrieval，2011，Bejing，China：625-634.

[4] PARK S，PENNOCK D，MADANI O，et al.Naive filterbots for robust cold-start reco-recommendations[C].In proceedings of the 12th ACM SIGKDD international conference on knowledge discovery and data mining，2006，Philadelphia，PA，USA：699-705.

[5]李穎，李永丽，蔡观洋.基于双重阈值近邻查找的协同过滤推荐算法[J].吉林大学学报（信息科学版）2013，31（6）：647-653.

[6] SARWAR B，KAPYPIS G，KONSTAN J，et al.Application of dimensionality reduction in recommender system：a case study [C] //Proceeding of the ACM Web KDD Workshop on Web Mining for E Commerce.New York，USA：ACM，2000：82-90.

[7]于世彩，谢颖华，王巧.协同过滤的相似度融合改进算法[J].计算机系统应用，2017，26（1）：135-140.

[8]黄创光，印鉴，汪静，等.不确定近邻的协同过滤推荐算法[J].计算机学报，2010，33（8）：1369-1377.

[9]陈宗言，颜俊.基于稀疏数据预处理的协同过滤推荐算法[J].计算机技术与发展，2016，26（7）：59-64.

[10]任看看，钱雪忠.协同过滤算法中的用户相似性度量方法的研究[J].计算机工程，2015，41（8）：18-22，31.

[11]夏建勋，吴非，谢长生.应用数据填充缓解稀疏问题实现个性化推荐[J].计算机工程与科学，2013，35（5）：15-19.

[12] ZHAO K， LU P Y. Improved collaborative filtering approach based on user similarity combination [C].International conference on management science & engineering，2014：238–243.