基于L1惩罚Logit模型的P2P网络借贷信用违约识别与预测
阮素梅 周泽林
(安徽财经大学1.金融学院 2.安徽经济社会发展研究院, 安徽 蚌埠 233000)
一、引言及相关文献综述
P2P网络借贷能够缓解资金供求双方的矛盾,然而贷款人信息的高度不对称性加大了贷款违约风险。大数据环境下,建立合理、准确的信用评估体系,有助于信贷机构对贷款人的信用评测,能够为控制违约发生的诱导因素提供决策参考,对于实现网络借贷平台平稳运行等具有重要意义。
经典的信用评估模型主要使用统计分析方法,例如Z-Score模型(Altman,1968)、ZETA模型(Altman et al.,1977)和Logit模型(Laitinen,1999)。这三种信用评估模型的核心理念在于建立信用水平及其影响因素之间的联系,进而实现信用状态的准确评估。这类方法发展时间较长,技术相对成熟,应用范围也最为广泛,前两种主要使用线性模型设计,第三种使用非线性的Logistic转换。吴世农等(2001)应用剖面分析和单变量分析,选定6个财务指标,应用Fisher判定分析、多元线性回归分析和Logit回归分析三种方法分别建立三种预测财务困境模型。Davis et al. (2008)与宁泽逵等(2016)主张Logit回归是全球早期预警系统和信号识别的最适当方法。韩立岩等(2010)运用主成分分析与Logit回归结合,建立国内外中小上市公司财务危机判别模型。王君萍等(2015)以我国能源上市企业为研究对象,进行指标选取和运用Logit回归构建预警模型。董晓林等(2017)基于二元选择Logit模型,研究城乡家庭金融资产选择问题。
为改进经典信用评估方法的模型误设缺陷以及对非线性处理能力的不足,机器学习领域的方法(主要有神经网络、支持向量机)被引入信用评估领域。在使用神经网络进行信用评估研究方面,代表性的文献有Desai et al. (1996)、王春峰等(1999)、Baesens et al. (2003)、Abdou et al.(2008)、Angelini et al.(2008)等。在使用支持向量机进行信用评估研究方面,代表性的文献有Baesens et al. (2003)、李建平等(2004)、Bellotti et al. (2009)、Yu et al. (2011)、余乐安(2012)、陈为民等(2012)、Harris(2013)、Xiao et al.(2017)等。实证研究表明基于机器学习方法的信用评估效果要优于其他方法,陈诗一(2008)、刘玉敏等(2016)、Hajek et al. (2017)等均发现向量机方法的预测准确度比Logit模型有明显改进,但并不总是最优。
信用评估实践的发展,积累了更多的影响因素,形成了高维数据(或称高维变量),需要从冗余变量中甄别出特征变量。以逐步回归为代表的子集变量选择法,需要进行多次重复计算操作,当数据变量众多时,该方法往往就不适用了(Breiman,1995;孙燕,2012)。Tibshirani(1996)提出的LASSO(Least Absolute Shrinkage and Selection Operator)回归,不仅能够进行变量选择,而且能够同时得到高维数据均值回归模型估计结果。有研究将高维数据回归分析方法引入信用评估领域,Perederiy(2009)、Koopman et al. (2011)、Amendola et al. (2012)、方匡南等(2014)分别使用LASSO方法进行高维变量选择与特征提取,建立信用评估模型。
自2012年以来,我国互联网金融蓬勃发展,对于小微企业融资具有重要意义(安宝洋,2014;Xu,2017)。皮天雷等(2014)、BenSaïda et al.(2017)、Zhang et al.(2017)等认为,P2P网络借贷作为互联网金融创新的典型代表,能够显著提高资金配置效率。在P2P市场中,日常用户活跃度高、交易量大,产生了大量的信用数据,具有典型大样本与高维特征,为信用评估模型开发带来了机遇与挑战(Serrano-Cinca et al.,2016;Blasco et al.,2017)。可以说,在信用评估领域,机器学习方法在模型的预测准确度方面已表现得很优越,并得到较高的认可度,但其缺点在于大多数模型采用复杂的非线性作用机制,既难以识别关键风险因子,也不便于管理者直观理解其经济含义。经典信用评估模型(如Logit模型)可能在预测精度方面不如机器学习模型,但可以清晰地表达各因子对信用状态的(转换后)线性影响与边际贡献,既能够进行风险预测,又有助于进行风险控制(蒋翠侠 等,2017)。因此,可以在经典信用评估模型基础上,进一步考虑模型的变量选择能力,提高其预测精度,解决P2P借贷中违约识别与预测这两个关键问题。
为此,本文将L1惩罚Logit模型应用于P2P网络借贷信用违约分析,一方面通过LASSO的变量选择功能,从众多影响因素中筛选出关键因素;另一方面,通过Logit模型,分析P2P网络借贷信用违约行为。利用拍拍贷的信用数据,实证检验了L1惩罚Logit模型效果,发现其能够很好地适应拍拍贷信用数据特征,揭示拍拍贷市场中信用行为与规律。本文的数值模拟结果与实证结果都表明:L1惩罚Logit模型具有很好的变量选择与预测功能,能够得到比其他模型(支持向量机模型、普通Logit模型)更好的预测效果,可以准确预测信用违约风险;而且能够识别信用违约的关键影响因素,细致地刻画各关键影响因素对违约概率带来的影响,可以为风险控制提供决策依据。
二、模型与方法
(一)L1惩罚Logit模型
在LASSO方法中,由于使用了绝对值惩罚(也称L1惩罚),能够实现变量选择。LASSO方法既可以和线性回归相结合,用于解决连续型变量的预测问题;也可以和Logit回归相结合,用于解决离散变量的分类问题。为此,可以将LASSO思想与Logit模型相结合,建立L1惩罚Logit模型,并将其应用于信用违约分析。
1.模型表示与估计
设第i个样本观测记为(x1i,x2i,…,xki,yi),其中:xi=(x1i,x2i,…,xki)为由解释变量组成的设计矩阵;yi为可观测的二元响应变量,取值为1或0,分别表示违约与非违约两种信用状态。标准的二元选择模型:
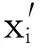
(1)
其中:i=1,…,n;y*i为不可观测的潜变量;εi为随机扰动项;β为k×1维待估计参数向量,可以通过下式求解:
(2)
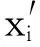
(3)
将LASSO变量选择思想融入二元选择分位数回归,即在式(2)中增加L1惩罚函数,得到:
(4)
其中:λ||β||1即为惩罚函数;||β||
1为β的向量1-范数;λ≥0为惩罚参数,取值越大,惩罚力度越大,取值越小,惩罚力度越小。模型的参数估计,可以采取Efron et al. (2004)提出的LARS算法。
2.惩罚参数选择
L1惩罚Logit模型的变量选择,关键在于惩罚参数λ的选取,常用方法有Bootstrap、交叉验证(Cross Validation,CV)等,本文采用10-折交叉验证(CV)方法确定惩罚参数λ的值,其具体算法如下:
(5)
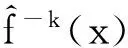
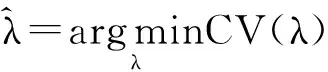
(6)
(二)分类效果评价
1.混淆矩阵
在两分类问题中,预测结果存在四种情形,详见表 1所示的混淆矩阵。通过混淆矩阵,能够容易得出一个模型的正确率为(a+c)/(a+b+c+d),第Ⅰ类错误率b/(a+b)和第Ⅱ类错误率d/(d+c),从而合理地评价模型效果。

表1 混淆矩阵
2.ROC曲线与AUC值
ROC曲线是根据截断值的变化而绘制出的一条曲线,每一个截断值对应于曲线上的一个点,其纵坐标为真阳性率(TPR),横坐标为假阳性率(FPR)。对于不同的分类模型,性能优者ROC曲线更接近左上角。在ROC曲线基础上,由ROC曲线下方区域的面积,得到AUC(Area Under ROC Curve)值,定义如下:
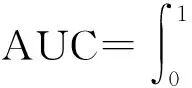
(7)
其中,TPR(FPR)表示击中率是误报率的一个函数,实际上就是ROC曲线。现实中,随机分类器所得AUC=0.5;完美分类器所得AUC=0.1;一般的分类器的AUC值介于0.5到1之间。AUC值越接近于1,说明诊断效果越好:AUC值在0.5~0.7时,有较低准确性;在0.7~0.9时,有一定准确性;在0.9以上时,有较高准确性。此外,AUC<0.5不符合真实情况,在实际中极少出现。
三、数值模拟
(一)数据生成
为检验L1惩罚Logit模型的变量选择能力与预测效果,进行Monte Carlo模拟。参考Tibshirani(1996)的“Example 4”,设计40个解释变量且任意两个解释变量xj与xk之间的相关系数为ρ|j-k|;回归系数β=(0,0,…,0,2,2,…,2,0,0,…,0,2,2,…,2)′,即连续10个0、连续10个2,反映解释变量对响应变量的影响程度。在式(1)基础上,设计响应变量生成机制,将式(1)改写为:
(8)
其中:εi~iidN(0,1),i=1,2,…,N。解释变量X=(x1,x2,…,x40)′来自一个多元标准正态分布,取ρ=0.5,代表中等相关程度;σ=15,表示信号噪音比约为9.0。
(二)模拟结果
实验中,设置样本量N=200,随机地取其中的100个样本用于模型估计,余下的100个样本用于模型预测。重复上述过程B=500次,变量选择结果见表2;记录下AUC、正确率和运行时间三个指标的均值与及标准差,结果见表3。实验的硬件配置为双处理器 Inter Xeon E5-2630L(六核,2.1GMHz)和 32GB 内存;软件配置为64位R 3.4.2。
由表2可知:无论是支持向量机模型还是普通Logit模型,都没有变量选择功能,始终选中没有贡献的变量x1,x2,…,x10与x21,x22,…,x30。L1惩罚Logit模型很好地实现了变量选择,不但能够将存在显著作用的变量x11,x12,…,x20与x31,x32,…,x40全部选中,而且能够将没有贡献的变量x1,x2,…,x10与x21,x22,…,x30进行删除,错误率仅为0.2%、…、0.4%与0.2%等,不超过0.4%。因此,L1惩罚Logit模型具有很好的变量选择能力。此外,就运行时间而言,普通Logit模型平均耗时最短,运行速度最快;其次为L1惩罚Logit模型;支持向量机模型则耗时较多。

表2 变量选择结果与运行时间
注:在变量选择结果中,数值大小表示在500次重复中变量被选中的次数;在运行时间结果中,均值表示500次重复中平均运行时间,标准差为运行时间标准差大小;普通Logit模型无需设置参数,L1惩罚Logit模型与支持向量机模型通过交叉验证选取了最优超参数(L1惩罚Logit模型中的惩罚参数和支持向量机模型中的核函数参数)。

表3 模型预测结果
由表3可知:就标准差大小而言,各模型都取得了稳定的预测结果。就均值而言,从正确率指标来看,L1惩罚Logit模型和支持向量机模型均取得了较好的结果,都优于普通Logit模型。从AUC指标来看,其均值水平都低于正确率指标,表明AUC指标是一个更为严苛的评价指标。实验结果表明,L1惩罚Logit模型的AUC均值明显优于普通Logit模型和支持向量机模型,表现出更为强大的预测能力。
综合表2和表3的结果,可以得到:L1惩罚Logit模型不但具有很好的变量选择能力,而且能够得到比较理想的预测效果。
四、应用研究
(一)样本和指标选取
本文的实证研究数据来源于科赛网(http://www.kesci.com)提供的拍拍贷公开脱敏数据,样本区间为2010年2月—2015年6月。原始数据中部分变量的数据缺失比例很高,这里删除了缺失比例超过10%的变量。经过数据清洗(删除缺失数据、数据匹配等),得到有效样本量9913。表 4列出了所有14个变量,其中:账户状态(status)为响应变量,取值为结清(212)、正常(246)、逾期(9455),占比分别为2.14%、2.48%和95.38%;其余13个变量为解释变量。
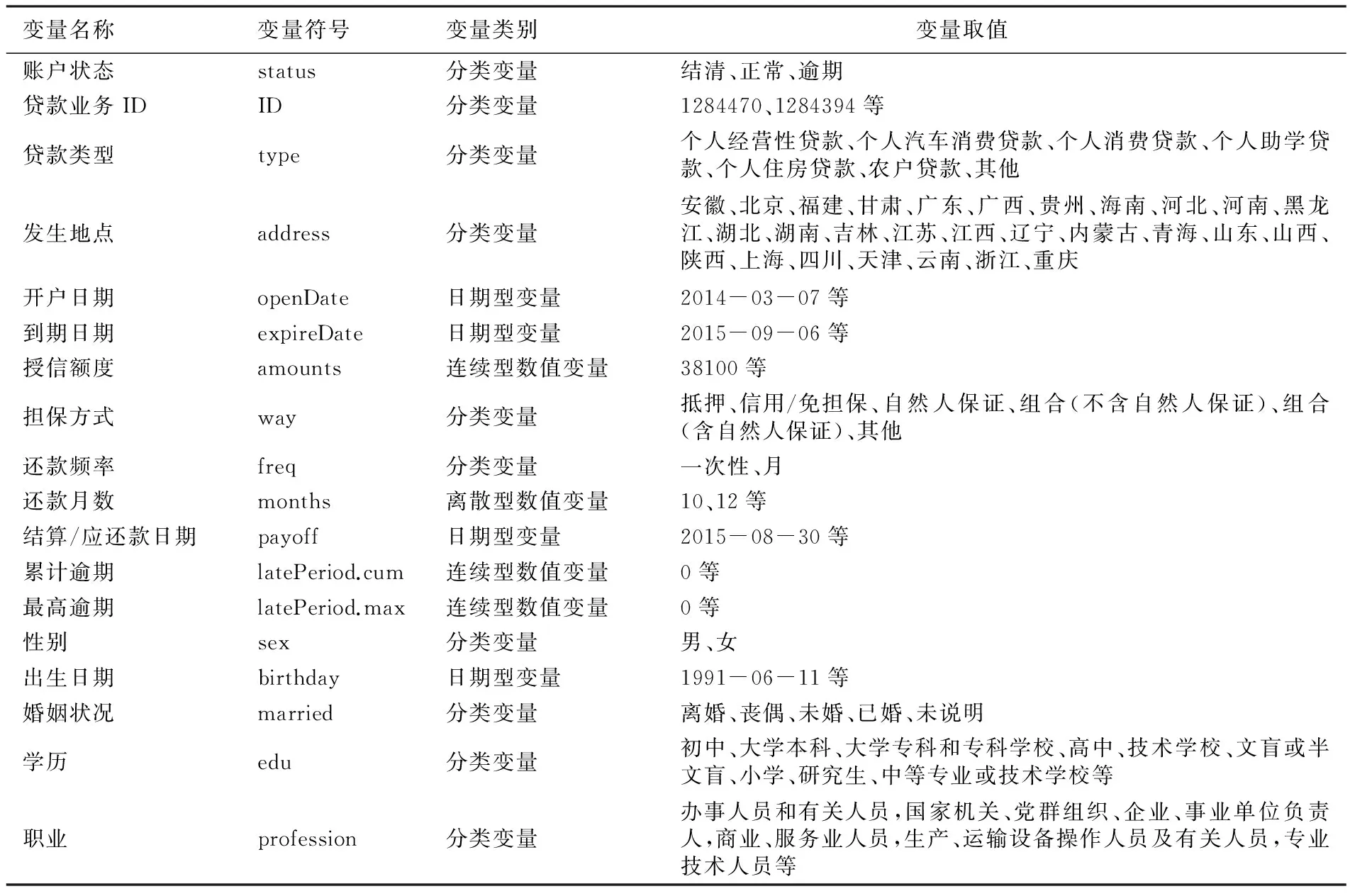
表4 变量说明
(二)立联表分析
这里,通过比例型立联表分析,初步查看贷款状态与教育程度、性别、婚姻状态之间的关系。

表5 贷款状态与教育的立联表分析
注:这里对原始数据的教育程度进行相应的归并,得到五个等级的教育水平:研究生、大学本科、大学专科、中学、小学及以下。
由表5可以看出,教育程度越高,结清比例越高,逾期比例越低;反之,则反是。如“小学及以下”信贷客户,其结清比例仅为1.96%(比“研究生”低近6个百分点),更多处于逾期状态,为96.27%(比“研究生”高近5个百分点),这意味着学历越高会越倾向于结清贷款。卡方检验结果(χ-squared=174.88,p-value=0.0004)表明,教育与贷款状态之间存在显著的关联关系。
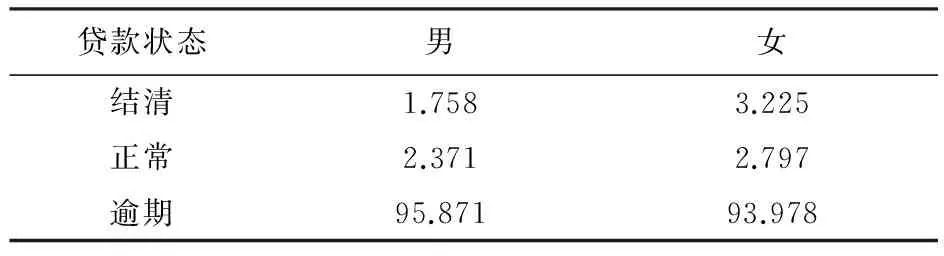
表6 贷款状态与性别的立联表分析
由表6可以看出,与男性相比,女性结清比例要高出1.5个百分点,逾期比例要低近2个百分点,表明女性客户更倾向于结清贷款。卡方检验结果(χ-squared=21.283,p-value=0.0009)表明,性别与贷款状态之间存在显著的关联关系。
由表7可以看出,在已婚状态下,结清比例最高,逾期比例最低;在丧偶状态下,结清比例较低(比已婚状态低近6个百分点),而逾期比例较高(比已婚状态高7个百分点以上),意味着婚姻状况越稳定越倾向于结清贷款。卡方检验结果(χ-squared=308.98,p-value=0.0005)表明,婚姻状态与贷款状态之间存在显著的关联关系。

表7 贷款状态与婚姻状况的立联表分析
(三)信用违约分析
1.变量选择与模型估计
首先,为了适应两分类讨论,本文将“逾期”视为违约,将“结清” 、“正常”视为非违约。
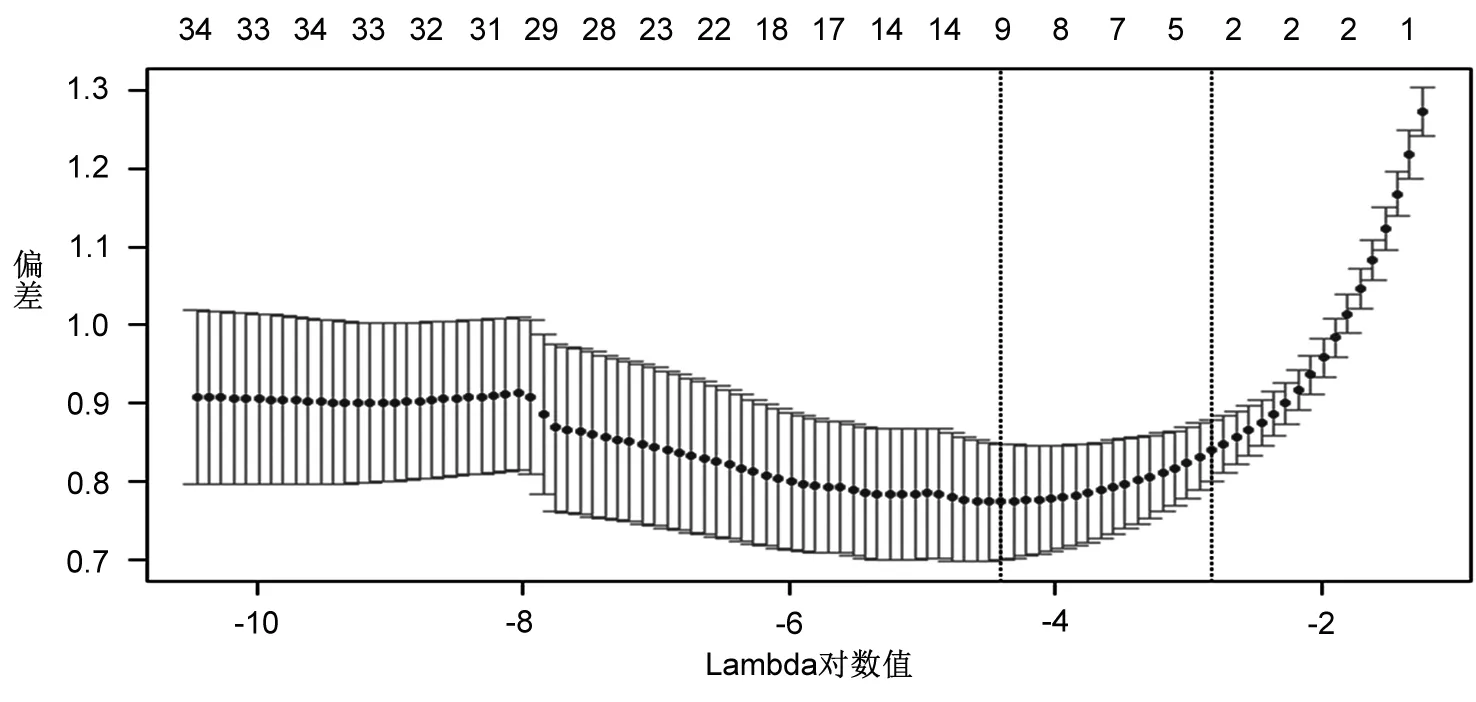

图1 交叉验证与选择过程
注:这里对原始数据的职业变量进行相应的归并,得到三个等级的职业水平:国家机关、党群组织、企业、事业单位负责人,专业技术人员及其他。
其次,通过交叉验证,对L1惩罚Logit模型参数进行选择,结果见图 1所示。根据Tibshirani(1996)的建议:在模型偏差相差不大的基础上,尽量获得相对比较重要的变量,使压缩程度最大,即获得的变量数目尽量少。为此,本文选取图 1中右侧虚线对应的值,得到模型解释变量系数有5个不为0,详见表 8。这样,管理者可以将主要精力集中到这5个变量上来,防范信用违约风险,极大地减少了从全部13个变量出发实施监管方案带来的管理成本。
最后,估计L1惩罚Logit模型选中变量的系数,详见表8。在存在显著影响的5个变量中,包含性别、学历与婚姻状态三个变量,与立联表所得结果一致。另外,在这5个变量中,性别、学历、婚姻状况、职业等对信用违约存在反向影响,而授信额度对信用违约存在正向影响。事实上,这一结果有较强的作用机理。例如学历越高,其还款能力越强,且还款意愿越强烈,最终违约可能性降低,因此呈现反向作用;授信额度越高,可能导致按时足额还款困难,最终违约可能性提高,因此存在正向影响。
2.模型性能比较
为了评价L1惩罚Logit模型的性能,将其与Logit模型、支持向量机模型(SVM)进行比较。利用上文描述的标准数据集,从中随机抽取75%数据作为训练集,剩下的25%作为测试集,分别使用上述模型与方法运行100次,记录下正确率、第Ⅰ类错误率、第Ⅱ类错误率、AUC值,进而统计出100次中其对应的均值与及标准差,结果见表 9。

表9 信用评价结果比较
由表 9可知,无论从模型的正确率,还是第Ⅰ类错误率或者第Ⅱ类错误率来考量,L1惩罚Logit模型的结果都是最优的,其次为支持向量机模型,最后为普通Logit模型。与其他两个模型相比,L1惩罚Logit模型具有更高的正确率和更低的错误率,特别是将Ⅰ类错误率降低近66%。不仅如此,L1惩罚Logit模型所得结果的标准差更小,意味着该模型具有更好的稳健性。当然,由于本文的数据集是一个典型的非平衡分类,正确率往往难以奏效,需要进一步观察其AUC值。AUC的评价结果表明,L1惩罚Logit模型的性能最优,比普通Logit模型提升13.87%,比支持向量机模型提升16.02%。究其原因,可能在于:L1惩罚Logit模型通过变量选择功能,将一些干扰变量的系数压缩为0,避免了一些冗余信息的干扰,提升了模型的预测性能。
综合来看,L1惩罚Logit模型在处理高维、非均衡数据时,表现出很好的效果:第一,选择出重要变量,对于控制信用违约发生具有重要决策参考意义;第二,能够得到更好的分类预测结果,提高了AUC等性能。
3.违约概率预测
鉴于L1惩罚Logit模型的优良表现,进一步使用其进行违约概率预测。在L1惩罚Logit模型筛选出的五个关键影响因素中,性别、学历、婚姻状况、职业等为分类变量,授信额度为连续变量(经过了自然对数变换)。为此,考虑如下四种类型的变量组合:(1)性别+授信额度;(2)学历+授信额度;(3)婚姻状况+授信额度;(4)职业+授信额度。在每一组合中,性别、学历、婚姻状况、职业等分类变量取各自的离散值,授信额度的取值按照从低到高依次等间隔选取500个,将其取值结果代入L1惩罚Logit模型中,可以预测出信用违约概率变动情况,分别见图2~图5。
由图2~图5可知,授信额度是违约的重要影响因素,且随着授信额度的增加,违约发生概率在不断增加,这与表8授信额度回归系数为正的结果一致。在图2中,男性的违约概率曲线始终位于女性的上方,表明在相同的授信额度情况下男性违约概率要大于女性,这与表8中性别回归系数为负以及表6中立联表分析结果一致。图3清晰地显示了不同学历在违约概率上的差异,可以发现:学历水平越高,违约可能性越低;反之,则反是。不过,违约概率在学历水平上的差异将被授信额度所替代,例如在授信额度达到12(原始值为162754)之后,不同学历群体的违约概率近乎相同。图4所得结果与图3类似,违约概率预测结果表明,婚姻状态越稳定,违约可能性越低,并且这一差距也被授信额度所替代。图5的表现与图2类似,国家机关等单位负责人、专业技术人员及其他三类群体在违约表现上存在着显著差异,其违约可能性依次递增,并且这一差异没有被授信额度所取代。这一结果意味着,无论在多高的授信额度下,国家机关等单位负责人的违约概率都是最低的,比专业技术人员和其他人员分别低约3%和7%。
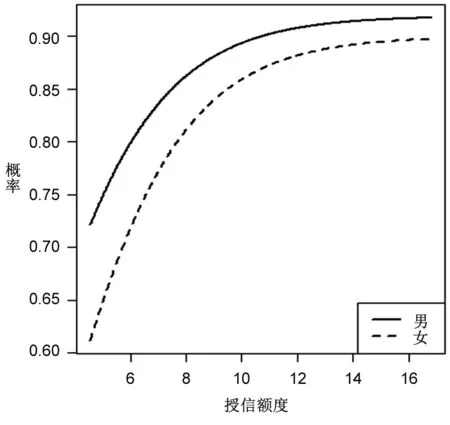
图2基于性别+授信额度的违约概率预测
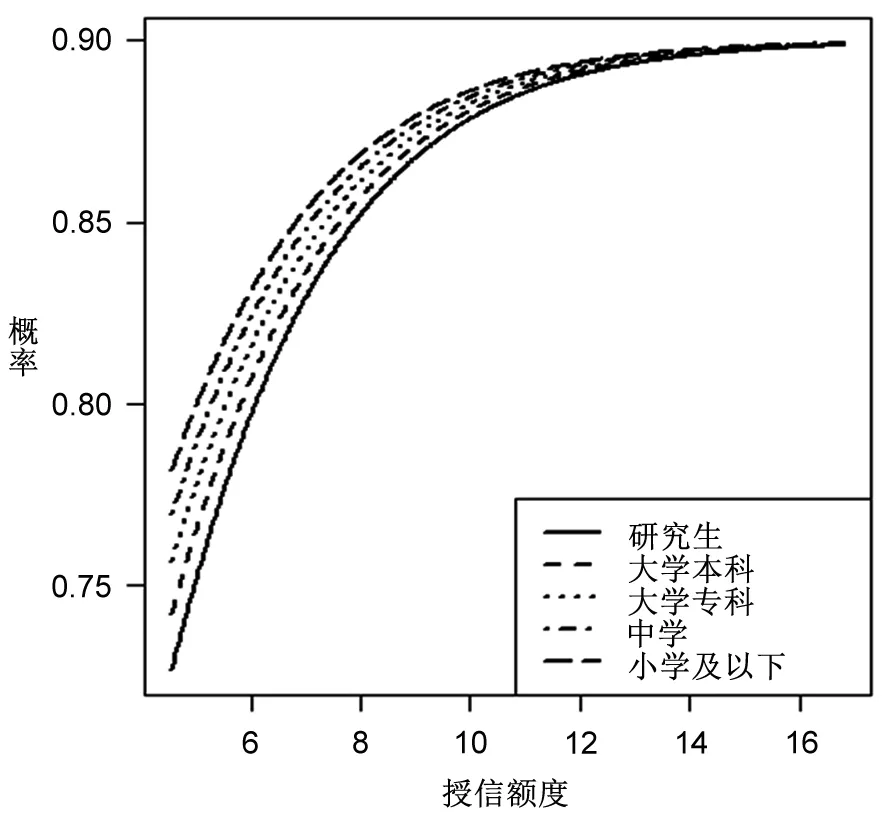
图3基于学历+授信额度的违约概率预测
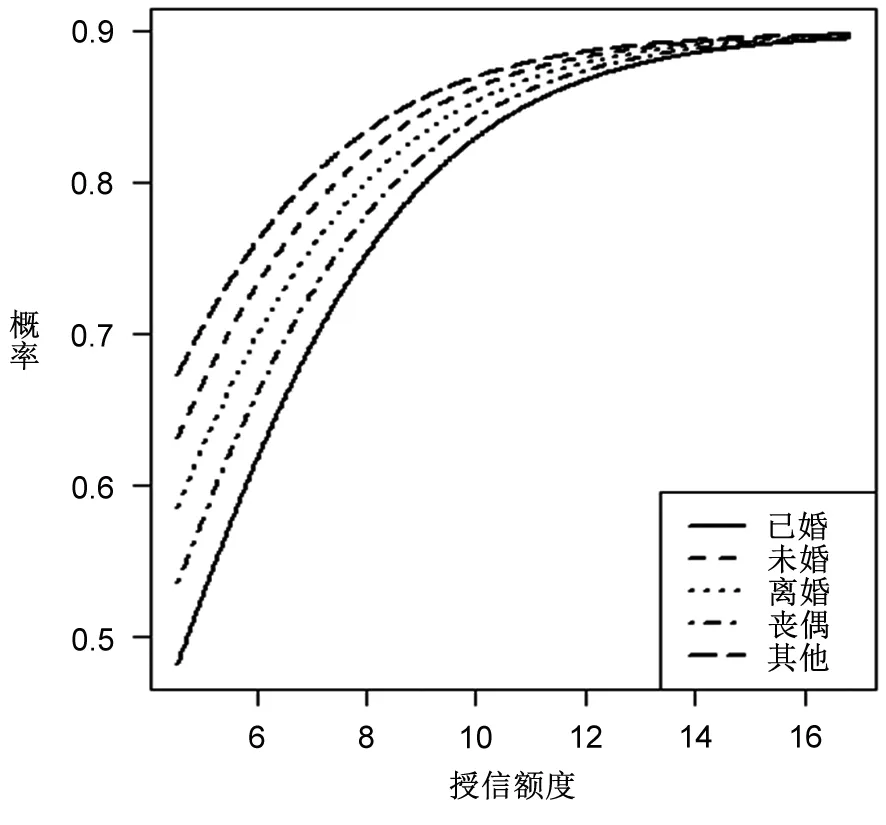
图4基于婚姻状况+授信额度的违约概率预测
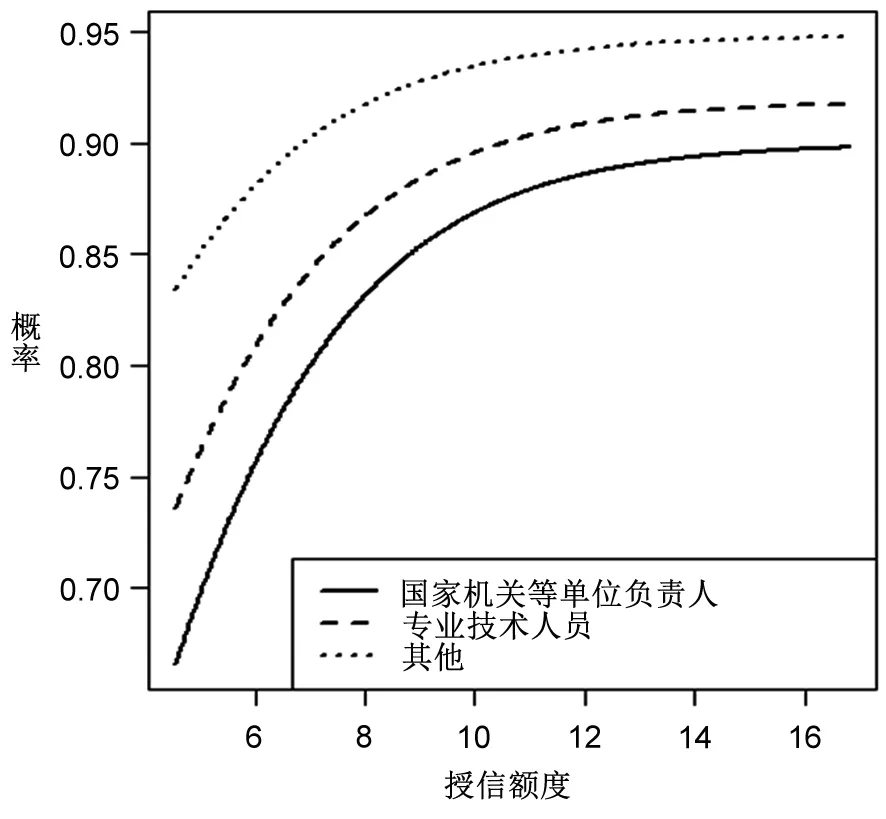
图5基于职业+授信额度的违约概率预测
五、结论与启示
金融理论与实践的迅速发展,积累了越来越多的金融大数据,表现出非均衡、非线性、高维等典型特征,为实现准确的信用评价带来了机遇与挑战。本文以P2P网络借贷为对象,研究其信用违约行为。考虑到P2P网络借贷中信用数据特征,本文将L1惩罚Logit模型应用于信用违约识别与预测,取得了一些实证结果,总结如下:
第一,L1惩罚Logit模型具有很好的变量选择功能与预测能力。通过Monte Carlo数值模拟,将L1惩罚Logit模型与普通Logit模型、支持向量机模型进行了对比。数值结果表明:在变量选择方面,L1惩罚Logit模型变量选择错误率仅为0.2%~0.4%,而普通Logit模型与支持向量机模型则不具备变量选择功能;在模型预测方面,L1惩罚Logit模型获得了更高的正确率和AUC值,预测能力更强;在运行时间方面,L1惩罚Logit模型稍逊于普通Logit模型,但优于支持向量机模型。
第二,L1惩罚Logit模型的变量选择功能和回归系数估计,克服了支持向量机等智能模型黑箱操作的弊端,增强了模型的解释性。通过变量选择功能识别出影响信用违约的关键指标,依据模型估计变量系数的正负来抑制或是促进相应信用特征以完成对风险的有效控制。例如学历的回归系数为负,意味着学历越高,信用违约可能性越低。从而可以通过提高学历(信贷对象为高学历者)的方式,降低P2P网络借贷信用违约风险。
第三,L1惩罚Logit模型提升了普通Logit模型的分类性能,能够得到更加准确、稳健的分类预测结果。本文的实证结果表明,L1惩罚Logit模型不仅能够显著地提升预测准确性(比普通Logit模型提升13.87%,比支持向量机模型提升16.02%),而且能够显著地降低第Ⅰ类错误率与第II类错误率,特别是将Ⅰ类错误率降低近66%,控制在6.4%的极佳水平。
第四,L1惩罚Logit模型能够细致分析关键影响因素对违约概率造成的影响。本文考虑了性别+授信额度、学历+授信额度、婚姻状况+授信额度、职业+授信额度等四种类型的变量组合,研究其对违约概率带来的影响,既有助于理解信用违约行为及其发展规律,预测信用违约的发生;也可以实现情景模拟,制订相应政策组合,控制信用违约的发生。
总之,L1惩罚Logit模型不但具有很好的预测能力,提升了经典信用评估模型的性能,而且具有很好的解释能力,改进了大多数机器学习模型复杂非线性作用机制难以直观理解的不足。一方面,L1惩罚Logit模型通过变量选择功能,可以有效地识别影响信用违约的关键因素,降低了管理者的监管成本;另一方面,L1惩罚Logit模型通过概率预测,既能够从总体上实现对信用违约状态的准确预测,又能够细致分析关键影响因素对违约概率造成的影响,有助于预测和控制信用违约的发生。
安宝洋. 2014. 互联网金融下科技型小微企业的融资创新[J]. 财经科学(10):1-8.
陈诗一. 2008. 德国公司违约概率预测及其对我国信用风险管理的启示[J]. 金融研究(8):53-71.
陈为民,张小勇,马超群. 2012. 基于数据挖掘的持卡人信用风险管理研究[J]. 财经理论与实践(5):36-40.
董晓林,于文平,朱敏杰. 2017. 不同信息渠道下城乡家庭金融市场参与及资产选择行为研究[J]. 财贸研究(4):33-42.
方匡南,章贵军,张惠颖. 2014. 基于Lasso-Logistic模型的个人信用风险预警方法[J]. 数量经济技术经济研究(2):125-136.
韩立岩,李蕾. 2010. 中小上市公司财务危机判别模型研究[J]. 数量经济技术经济研究(8):102-115.
蒋翠侠,黄韵华,许启发. 2017. 基于Lasso二元选择分位数回归的上市公司信用评估[J]. 系统工程(2):16-24.
李建平,徐伟宣,刘京礼,等. 2004. 消费者信用评估中支持向量机方法研究[J]. 系统工程(10):35-39.
刘玉敏,刘莉,任广乾. 2016. 基于非财务指标的上市公司财务预警研究[J]. 商业研究(10):87-92.
宁泽逵,宁攸凉. 2016. 区位、非农就业对中国家庭农业代际传承的影响:基于陕西留守农民的调查[J]. 财贸研究(2):75-84.
皮天雷,赵铁. 2014. 互联网金融:逻辑、比较与机制[J]. 中国经济问题(4): 98-108.
孙燕. 2012. 随机效应Logit计量模型的自适应Lasso变量选择方法研究:基于Gauss-Hermite积分的EM算法[J]. 数量经济技术经济研究(12):147-157.
王春峰,万海晖. 1999. 基于神经网络技术的商业银行信用风险评估[J]. 系统工程理论与实践(9):24-32.
王君萍,白琼琼. 2015. 我国能源上市企业财务危机预警研究[J]. 经济问题(1):109-113.
吴世农,卢贤义. 2001. 我国上市公司财务困境的预测模型研究[J]. 经济研究(6):46-55.
余乐安. 2012. 基于最小二乘近似支持向量回归模型的电子商务信用风险预警[J]. 系统工程理论与实践(3):508-514.
ABDOU H, POINTON J, El-MASRY A. 2008. Neural nets versus conventional techniques in credit scoring in Egyptian banking [J]. Expert Systems with Applications, 35(3):1275-1292.
ALTMAN E I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy [J]. The Journal of Finance, 23(4):589-609.
ALTMAN E I, HALDEMAN R G, NARAYANAN P. 1977. ZETATM analysis:a new model to identify bankruptcy risk of corporations [J]. Journal of Banking and Finance, 1(1):29-54.
AMENDOLA A, RESTAINO M, SENSINI L. 2012. Dynamic statistical models for corporate failure prediction in Italy [J]. Journal of Modern Accounting and Auditing, 8(8):1214-1224.
ANGELINI E, DI TOLLO G, ROLI A. 2008. A neural network approach for credit risk evaluation [J]. The Quarterly Review of Economics and Finance, 48(4):733-755.
BAESENS B, SETIONO R, MUES C, et al. 2003. Using neural network rule extraction and decision tables for credit-risk evaluation [J]. Management Science, 49(3):312-329.
BELLOTTI T, CROOK J. 2009. Support vector machines for credit scoring and discovery of significant features [J]. Expert Systems with Applications, 36(2):3302-3308.
BENSAÏDA A. 2017. Herding effect on idiosyncratic volatility in US industries [J]. Finance Research Letters, 23:121-132.
BLASCO N, CORREDOR P, FERRERUELA S. 2017. Can agents sensitive to cultural, organizational and environmental issues avoid herding [J]. Finance Research Letters, 22:114-121.
BREIMAN L. 1995. Better subset regression using the nonnegative garrote [J]. Technometrics, 37(4):373-384.
DAVIS E P, KARIM D. 2008. Comparing early warning systems for banking crises [J]. Journal of Financial Stability, 4(2):89-120.
DESAI V S, CROOK J N, OVERSTREET G A, Jr. 1996. A comparison of neural networks and linear scoring models in the credit union environment [J]. European Journal of Operational Research, 95(1):24-37.
EFRON B, HASTIE T, JOHNSTONE I, et al. 2004. Least angle regression [J]. Annals of Statistics, 32(2):407-499.
HAJEK P, HENRIQUES R. 2017. Mining corporate annual reports for intelligent detection of financial statement fraud-a comparative study of machine learning methods [J]. Knowledge-Based Systems, 128:139-152.
HARRIS T. 2013. Quantitative credit risk assessment using support vector machines: broad versus narrow default definitions [J]. Expert Systems with Applications, 40(11):4404-4413.
KOOPMAN S J, LUCAS A, SCHWAAB B. 2011. Modeling frailty-correlated defaults using many macroeconomic covariates [J]. Journal of Econometrics, 162(2):312-325.
LAITINEN E K. 1999. Predicting a corporate credit analyst′s risk estimate by logistic and linear models [J]. International Review of Financial Analysis, 8(2):97-121.
SERRANO-CINCA C, GUTIERREZ-NIETO B. 2016. The use of profit scoring as an alternative to credit scoring systems in peer-to-peer (P2P) lending [J]. Decision Support Systems, 89:113-122.
TIBSHIRANI R. 1996. Regression shrinkage and selection via the lasso [J]. Journal of the Royal Statistical Society: Series B, 58(1):267-288.
XIAO J, CAO H, JIANG X, et al. 2017. GMDH-based semi-supervised feature selection for customer classification [J]. Knowledge-Based Systems, 132(Supplement C):236-248.
XU J. 2017. China′s internet finance: a critical review [J]. China & World Economy, 25(4):78-92.
YU L, YAO X, WANG S, et al. 2011. Credit risk evaluation using a weighted least squares SVM classifier with design of experiment for parameter selection [J]. Expert Systems with Applications, 38(12):15392-15399.
ZHANG Z, HUNG K, CHANG T. 2017. P2P Loans and bank loans, the chicken and the egg, what causes what? Further evidence from a bootstrap panel granger causality test [J]. Applied Economics Letters, 24(19):1358-1362.

