“解二元一次方程组”教学的几点反思

◎张先进

(福建省三明市第四中学，福建 三明 365001)

新北师大版数学八年级上册5.2解二元一次方程组课时1，设计如下的教学过程：

师问1：大家会算出等式2□+1=5中“□=______”.

生：大笑，2.(响亮回答)

师问2：比如，这个等式2□+1=□+6中“□=______”.

生：(一会儿)5，5，5，……(声音不断传出)

师：很好，这两个问题卡不住你们，下面我们再来几题，准备好了吗？

生(跃跃欲试)

生：□=2，△=1.

师：你们是如何算出来的？(提问甲)

甲：先算出第一个式子中□=2，再把□=2代入另一个式子中求得△=1.

师：大家都是这么想吗？

生：是.(声音有点不够响)

师：想不想再来一题？

生：好！

生沉默，继而互相交流.

师巡视解答情况.

几分钟后，有学生回答：“□=3，△=2.”但大多数还未解出.(再过几分钟)

师：现在请同学们来说说你是如何算出来的.

乙：我发现第二个式子可得□=1+△，代入第一个式子算出△=2，从而□=3.

师：有没有不同的解法？

丙：老师，我是猜的.(学生们哄堂大笑)

师：很好，猜出来也是本事，大家都可以猜猜.

丁：我是由第一个式子得□=5-△，代入第二个式子中得△=2，从而□=3.

戊：老师，我发现两个式子相加，2□=6，所以□=3，△=2.

师：大家看看果真如此吗？这名同学好眼力，你们看出来了吗？还有吗？……

师：首先，我要表扬这几名同学，以及算出来的其他人，没算出来的也没关系，听了他们的算法，你们有所收获吗？其次，你们笑猜出答案的同学，“猜”也是一种技巧，数学中很重要，这是一种本能的直觉.最后，其他同学加油，我们还要继续吗？

生：想.(没算出来的学生跃跃欲试，机会来了)

生：哇，这么难.(学生思考中，师巡视指导解答)

师：同学们，今天的课上完了，方法也教了，你们也学了，不是吗？

生：老师，我们不明白，你能讲如何解二元一次方程组吗？

师：好，大家注意听讲.如果将上述几个式子中的“□，△”用字母x，y示，大家能得到什么？刚才我们知道前两个方程组的解，也了解如何求，那么如何正确求解呢？讲解例题：

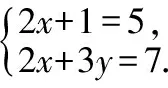
①

②

解由①得2x=5-1，x=2.

把x=2代入②中得y=1.

①

②

解由①得x=5-y.

③

把③代入②中得(5-y)-y=3，y=1.

把y=2代入③中得x=4,

反思1 激发兴趣

课标在课程实施建议中指出：“数学教学要紧密联系学生的生活实际，从学生的生活经验和已有知识出发，创设生动有趣的情境，为学生提供从事数学活动的机会，激发学生对数学的兴趣以及学好数学的愿望.”本课数学情境的创设从形式走向实质，将方程中的x，y先用图形“□，△”来表示，让学生认识如何求“□，△”值的过程，转化成抽象的含有字母x，y的二元一次方程组的解的过程.学生在上课过程中积极参与，不同程度的学生都有一定的收获.

反思2 形式淡化

注重实质，形式适度.传统教学是按知识的逻辑顺序讲解：概念→例子→练习，而新课程一般是从问题出发，在解决问题的过程中引出相关的概念和结论，力图让学生在“做”中领悟知识，培养学生自主学习的能力.本课的教学，一开始，从学生熟悉的图形等式算数入手，再过渡到较为复杂的题目，出现了不会解决的问题，从而发现可以用数学的方法来解，自然讲解抽象含x，y的二元一次方程组的解法，其实用含“□，△”图形等式求数与含x，y的二元一次方程组本质是一样的，只是形式不同罢了.

反思3 新旧结合

本课的教学，在会解一元一次方程基础上，探究如何求解二元一次方程组，教学的关键在于消元，二元转化成一元而已.本课将“新知识”转化成“旧知识”，从学生已有的数学知识出发，结合教材内容，创设情境，设疑引思，用学生熟悉的生活经验作为实例，引导学生利用自身已有的经验探索新知识，解决新问题.从了解求图形中“□，△”的值，再到抽象的问题，对解二元一次方程组，学生已有了初步的认识，对于如何求解二元一次方程组就不会那么难理解与掌握.

反思4 留下“尾巴”

反思5 数学课到底教了什么

数学给予学生带得走的能力是什么？忘却了所有的数学概念、公式与原理之后留下来的又是什么？

数学大师陈省身先生写下了“数学好玩”，数学好玩在于它的实质，而不在于它的形式.本节课的入手之处就在于“好玩”，学生从实际动手中发现数学的本质，将已有的知识转化成数学知识，再利用数学知识解决实际问题，在愉快的教学中完成授课任务.