湿热老化及应变率耦合作用下有机玻璃的微纳米力学性能

李林涛，王志华，金 涛

(太原理工大学 应用力学与生物医学工程研究所，太原 030024)

有机玻璃(PMMA)广泛用于生产生活各个方面，如仪表面板、橱窗、眼镜等[1-4]，因此，PMMA在使用过程中会经历不同的工况，如不同应变率、载荷条件和环境条件等。LI et al[5]研究发现PMMA的屈服应力随应变率的增加而增大，同时还建立了聚合物材料在承受外载荷时，其屈服行为表现出明显的静水压力依赖性以及温度和应变速率敏感性[6]。JIN et al研究了PMMA在压剪复合应力下的准静态时效性，提出环境条件对PMMA的力学性能有重要的影响[7-8]。MAHAJAN et al[9]表明非晶聚合物的物理老化温度远低于其玻璃化转变温度，从而导致其物理性质的变化。类似地，老化通常伴随着热力学、机械和其他物理性质变化[10]。纳米压入仪作为目前较为先进的材料表面接触力学性能测试仪器，可以连续精确地记录局部压入载荷和深度，基于接触理论和所得载荷-深度曲线可获得被测试材料的硬度、模量等参数，提供了一种可应用于金属、陶瓷、高聚物、复合材料、表面工程系统、微系统器件和生物材料的近乎无损的力学性能测试手段[11]。压痕测试方法通过DUTTA et al[12]的发展已经广泛用于聚合物材料的性能测试中。

本文通过微压入法对PMMA在湿热老化及应变率耦合作用下的力学性能进行了研究。实验采用5种不同应变率对不同老化时间的PMMA试样进行测试。由于PMMA多服役于潮湿环境，本文综合考虑了应变率和湿热老化的耦合作用，与材料实际服役工况更为贴近。

1 实验方法

试样是由Degussa公司提供的厚度为5 mm的AG Plexiglas○RPMMA，根据JEDEC国际标准，采用温度为85 ℃、相对湿度为85%的加速老化实验条件，将PMMA试样放入高温高湿时效箱中进行老化处理，设置不同老化时间为：0，1，4，7，10，13，19，22，25，28，30，33 d.实验采用 Agilent Technologies Inc.生产的配备CSM(连续刚度测量法)模块的Nano Indenter G200测试系统进行压入实验测量，压头为三棱锥Berkovich金刚石压头。实验应变率分别为0.01，0.03，0.05，0.1，0.2 s-1，最大压入深度2 000 nm.连续刚度测量法得到的载荷-时间曲线如图1所示，主要包括3个阶段：加载段、保载段、卸载段。连续刚度测量法(CSM)在文献[13-15]中已做了详细的介绍，通过实验得到的数据能够计算出接触刚度K[12，16]：

(1)

式中：Famp为激励载荷幅值；hamp为位移幅值；φ为响应位移滞后于激励载荷的相位角；m为压杆质量；ω=2πf为角频率；Kf，Ks分别为机架刚度和支撑弹簧刚度。三棱锥Berkovich金刚石压头的接触面积为：

(2)

其中，hc为接触深度，有以下关系

(3)

其中，F为保载载荷；ε为与压头形状有关的常数，玻氏压头ε=0.75.硬度可以表示为：

(4)

作为压头和被测试材料弹性性能的综合响应，缩减模量Er可以表示为

(5)

其中，β为压头形状相关常数，玻氏压头β=1.034.由式(5)可以得到被测试材料的弹性模量[12,15-16]:

(6)

式中：Ei,υi，E,υ分别为压头和被测材料的弹性模量和泊松比。对于金刚石压头Ei=1 141 GPa，υi=0.07，实验在室温下进行，每组实验重复3次。

图1 连续刚度测量法载荷-时间(F-t)示意图Fig.1 Schematic load-time (F-t) input function for CSM technique

2 实验结果与讨论

2.1 湿热老化对PMMA力学性能的影响

PMMA在不同老化天数下的载荷-位移曲线如图2所示，可以看出未经老化和老化过的PMMA试样有明显不同。在相同的位移条件下，未经老化的试样所需要的载荷更大，表明PMMA对湿热老化条件的敏感性。根据式(1)可以得到保载阶段的接触刚度，如图3所示，接触刚度随位移的增加而线性增加，拟合得到老化0,1,4,7,10,13,19,22,25,28,30，33 d的斜率分别为26.54,27.58,27.30,27.87,28.08,27.77,27.4,27.73,27.60,27.41,27.47,27.34 (N·m-1)/nm，弹性模量的变化斜率是随老化天数的增加而增加，而后减小逐渐趋于稳定。

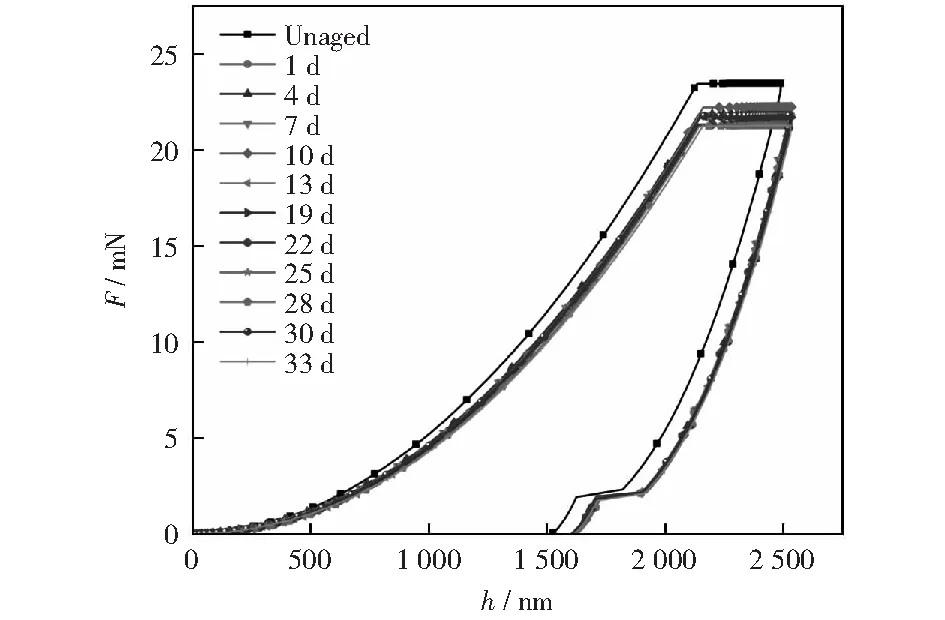
图2 PMMA在不同老化天数的载荷-压入深度曲线Fig.2 Typical recording of load versus depth during indentation of PMMA under different hygrothermal aging times

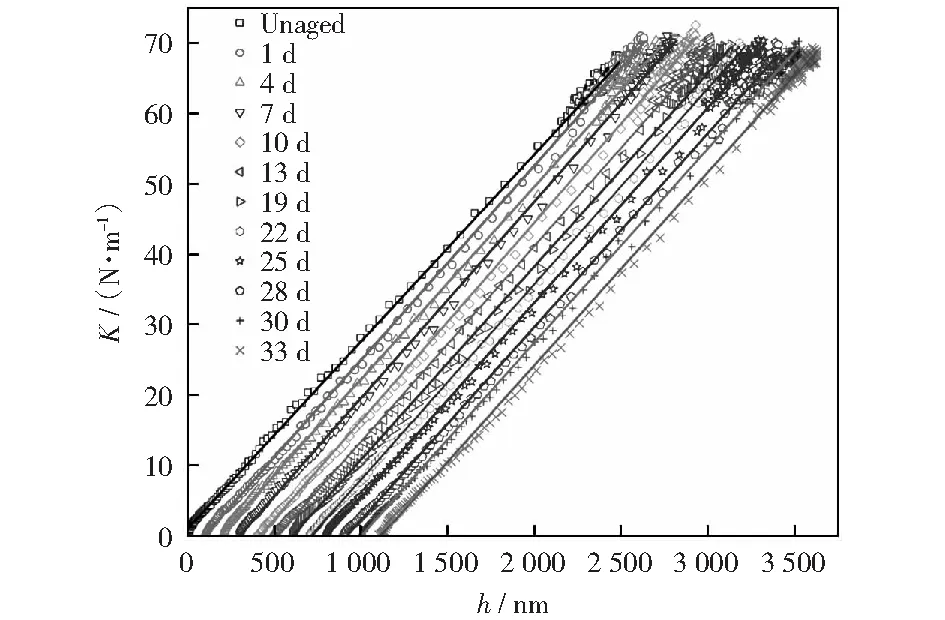
图3 PMMA试样不同老化天数下接触刚度与压入深度的关系Fig.3 Contact stiffness of PMMA samples under different aging time plotted against depth

提取压入保载阶段的位移和时间数据并对其进行归零化处理，得到PMMA保载段的蠕变位移-保载时间曲线，如图4所示。保载初期其蠕变位移迅速增加，随着保载时间的延长蠕变位移增速稳定。未经老化的PMMA试样蠕变变形较小，表明湿热环境导致PMMA微观结构发生了改变。

图4 湿热老化后PMMA的蠕变变形Fig.4 Creep displacement of PMMA sample under different aging times plotted against the holding time

图5和图6分别给出了弹性模量-深度和强度-深度曲线，通常将压入深度为500～1 900 nm时测得的弹性模量和硬度值作为单一测量结果。从图5中可以看出，压深在500 nm之后，弹性模量和硬度趋于平稳，因此取压深在500～1 900 nm之间的弹性模量和硬度值做后续分析。

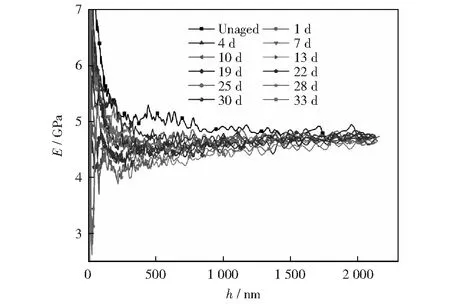
图5 PMMA弹性模量随压入深度变化曲线Fig.5 Elastic modulus-depth curves of PMMA

图6 PMMA硬度随压入深度变化曲线Fig.6 Hardness-depth curves of PMMA

图7给出了弹性模量和硬度随老化天数的变化曲线。对于弹性模量，在湿热老化开始阶段(0～10 d)有明显减小，GUAN et al[17]在环氧树脂中也发现相同的现象。在老化10～22 d之间，弹性模量的分散程度增加；当老化22 d之后，弹性模量开始趋于稳定。硬度与弹性模量表现出同样的趋势。因此，可以将湿热老化对PMMA的影响分为3个阶段：开始阶段(0～10 d)、不稳定阶段(10～22 d)、稳定阶段(22～33 d).进一步的研究还有待进行，出现这种现象的原因可能是，在开始阶段湿热老化对PMMA分子链间相互作用的影响降低了弹性模量和硬度；不稳定阶段在湿热老化的长时间作用下材料成分开始发生变化；在最后稳定阶段时PMMA之前的扰动体系逐渐平衡，因此弹性模量和硬度表现得稳定起来。

图7 湿热老化后PMMA的弹性模量和硬度变化Fig.7 Elastic modulus and hardness of PMMA as a function of aging time

2.2 应变率效应对PMMA力学性能的影响

分析4种老化天数在5种应变率下的载荷-位移曲线(如图8)，随着应变率的提高，达到相同压入深度所需的压入载荷不断增大，PMMA表现出明显的应变率效应。同样根据式(1)，计算得到不同应变率下的接触刚度(如图9),可知PMMA的接触刚度随压入深度线性增加。相关的理论[18-19]与实验结果表明，一般材料压入过程中接触刚度与压入深度呈线性关系。

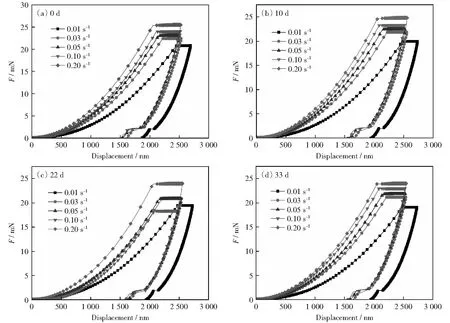
图8 在不同应变率和4种老化天数下的载荷-压力深度曲线Fig.8 Typical recording of load versus depth during indentation tests under different strain-rates

对PMMA在不同应变率下的接触刚度-压深曲线进行线性拟合得到其斜率，如表1所示。随着加载应变率的增加，接触刚度-深度曲线的斜率逐渐增大，表明PMMA在高应变率下刚度较大。

表1 不同应变率下接触刚度-深度曲线的斜率Table 1 Slopes of contact stiffness-depth curves under different strain rate

同样根据式(2)-(6)的计算得到不同应变率下的弹性模量和硬度，如图10所示,在高应变率下弹性模量较高，主要是由于高应变率下接触刚度增大；同样硬度也表现出应变率效应，由于高应变率下硬度较高，所以达到相同压入深度所需的载荷也增大，如图8所示。

对于粘弹性材料，试样在相应的恒定载荷下发生蠕变变形，保载阶段的蠕变应变率定义为[20]：

(7)

由图11可以发现，加载段应变率越高，相应的保载段蠕变位移就越大。对于粘弹性材料，高应变率加载下其粘性变形不能充分释放，转变为保载段更显著的蠕变变形；蠕变应变率随保载时间的延长而逐渐减小，且高应变率下保载初始段的蠕变应变率较大。

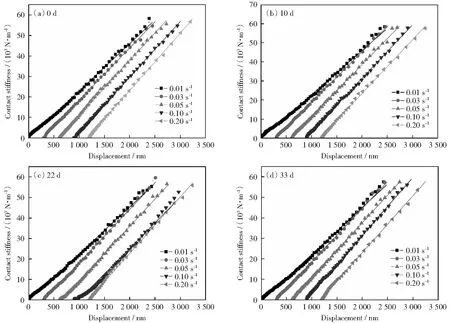
图9 在不同应变率和4种老化天数下的接触刚度-位移曲线Fig.9 Contact stiffness measured by CSM under different strain rate

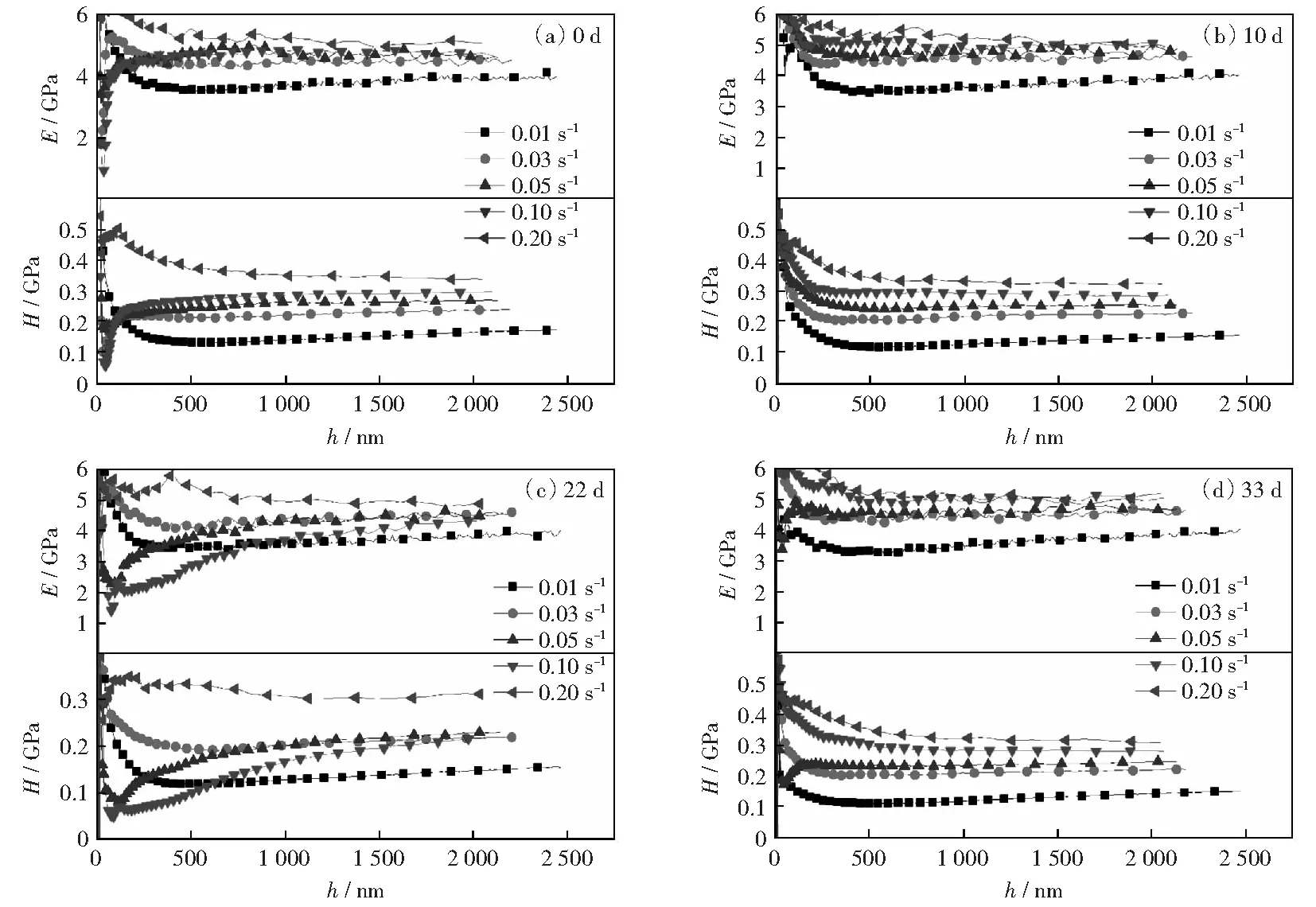
图10 不同应变率下的弹性模量-深度曲线Fig.10 Representative elastic modulus-depth curves under different strain rate

3 结论

基于微压入法，采用不同湿热老化天数(0,1,4,7,10,13,19,22,25,28,30，33 d)及5种加载应变率(0.01 s-1，0.03 s-1，0.05 s-1，0.1 s-1，0.2 s-1)对PMMA的湿热老化及应变率敏感性进行了研究，相关结论如下：

PMMA的力学性能对湿热老化和应变率都较为敏感。湿热老化的影响可分为3个阶段：初始阶段(0～10 d)、不稳定阶段(10～22 d)和稳定阶段(22～33 d).初始阶段弹性模量和硬度随老化天数的增加而减小，然后开始不稳定，随着老化天数的增加弹性模量和硬度趋于稳定；应变率敏感性主要表现为：高应变率加载下PMMA的粘性变形不能充分释放，因此相同压入深度下，高加载应变率所对应的压入载荷较大。基于连续刚度测量法(CSM)所得的PMMA接触刚度与压入深度呈线性关系，其斜率随加载应变率增加而增大。高应变率下PMMA弹性模量较大。基于保载段数据得到PMMA的蠕变位移和蠕变应变率，高应变率加载下PMMA的粘性变形不能充分释放，转变为保载段更为显著的蠕变变形及较高的初始蠕变应变率。作为粘弹性材料，PMMA的力学性能对湿热老化及加载应变率有较强敏感性，实际使用中需要对环境及加载条件进行考虑。

图11 不同应变率下保载段的蠕变位移和蠕变应变率Fig.11 Creep displacement and creep strain rate during the holding stage under different strain rate

[1] MULLIKEN A D,BOYCE M C.Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates[J].International Journal of Solids & Structures,2006,43(5):1331-1356.

[2] WU H,MA G,XIA Y.Experimental study of tensile properties of PMMA at intermediate strain rate[J].Materials Letters,2004,58(29):3681-3685.

[3] NOGUEIRA T,BOTAN R,WYPYCH F,et al.Study of thermal and mechanical properties of PMMA/LDHs nanocomposites obtained by in situ,bulk polymerization[J].Composites Part A Applied Science & Manufacturing,2011,42(8):1025-1030.

[4] AYRE W N,DENYER S P,EVANS S L.Ageing and moisture uptake in polymethyl methacrylate (PMMA) bone cements[J].Journal of the Mechanical Behavior of Biomedical Materials,2014,32(4):76-88.

[5] LI Z,LAMBROS J.Strain rate effects on the thermomechanical behavior of polymers[J].International Journal of Solids & Structures,2001,38(20):3549-3562.

[6] FARROKH B,KHAN A S.A strain rate dependent yield criterion for isotropic polymers:Low to high rates of loading[J].European Journal of Mechanics - A/Solids,2010,29(2):274-282.

[7] JIN T,ZHOU Z,WANG Z,et al.Quasi-static failure behaviour of PMMA under combined shear-compression loading[J].Polymer Testing,2015,42:181-184.

[8] COLOM X,GARCA T,SUOL J J,et al.Properties of PMMA artificially aged[J].Journal of Non-Crystalline Solids,2001,287(1/2/3):308-312.

[9] MAHAJAN D K,ESTEVEZ R,BASU S.Ageing and rejuvenation in glassy amorphous polymers[C]∥Multi-point Interaction with Real and Virtual Objects.Berlin Heidelberg:Springer,2010:177-188.

[10] RIHA P,HADAC J,SLOBODIAN P,et al.Effect of aging time on the volumetric and enthalpic glass transition of a-PMMA upon heating[J].Polymer,2007,48(25):7356-7363.

[11] LEE S H,WANG S,PHARR G M,et al.Evaluation of interphase properties in a cellulose fiber-reinforced polypropylene composite by nanoindentation and finite element analysis[J].Composites Part A Applied Science & Manufacturing,2007,38(6):1517-1524.

[12] DUTTA A K,PENUMADU D,FILES B.Nanoindentation testing for evaluating modulus and hardness of single-walled carbon nanotube-reinforced epoxy composites[J].J Mater Res,2004,19:158-164.

[13] XIAO G,YUAN G,JIA C,et al.Strain rate sensitivity of Sn-3.0Ag-0.5Cu solder investigated by nanoindentation[J].Materials Science & Engineering A,2014,613(9):336-339.

[14] JEE A Y,LEE M.Comparative analysis on the nanoindentation of polymers using atomic force microscopy[J].Polymer Testing,2010,29(1):95-99.

[15] HODZIC A,STACHURSKI Z H,KIM J K.Nano-indentation of polymer-glass interfaces：Part I.Experimental and mechanical analysis[J].Polymer,2000,41(18):6895-6905.

[16] JAKES J E,LAKES R S,STONE D S.Broadband nanoindentation of glassy polymers:Part II.Viscoplasticity[J].Journal of Materials Research,2012,27(2):475-484.

[17] GUAN Y,CHEN X,LI F,et al.Study on the curing process and shearing tests of die attachment by Ag-epoxy electrically conductive adhesive[J].International Journal of Adhesion & Adhesives,2010,30(2):80-88.

[18] CHENG Y T,CHENG C M.Scaling,dimensional analysis,and indentation measurements[J].Materials Science & Engineering Reports,2004,44(4/5):91-149.

[19] 谭孟曦.利用纳米压痕加载曲线计算硬度-压入深度关系及弹性模量[J].金属学报,2005,41(10):1020-1024.

TAN M X.Extracting hardness-displacement relation and elastic modulus using nanoindentation loading curves[J].Acta Metallurgica Sinica,2005,41(10):1020-1024.

[20] MAYO M J,NIX W D.A micro-indentation study of superplasticity in Pb,Sn,and Sn-38 wt% Pb[J].Acta Metallurgica,1988,36(8):2183-2192.