基于多项式平方和规划的涡扇发动机切换控制

孙昊博，潘慕绚，黄金泉

（南京航空航天大学江苏省航空动力系统重点实验室，南京210016）

0 引言

航空发动机是高度复杂的非线性系统，动态特性随工作状态和飞行条件的变化而不断改变[1]。为了使航空发动机控制系统在整个飞行包线内满足控制要求，目前多是在线性控制理论的框架内采用传统变增益方法设计控制器。然而传统的变增益控制要求系统的参数变化必须是缓慢的，无法满足航空发动机快速变化的动态特征的要求[2]。针对这一问题，目前工程上广泛应用线性变参数（Linear Parameter Varying,LPV）增益调度方法进行控制器综合[3]。LPV变增益控制的控制器增益随调度参数的变化而变化。与传统变增益相比，LPV变增益控制不要求系统参数变化是缓慢的。在LPV控制器的求解上，通常将控制器的求解问题转换成线性矩阵不等式（Linear Matrix Inequality,LMI）约束下的优化问题，然后应用工具箱进行求解[4]。然而对于多项式形式的LPV模型，LMI方法会带来较大保守性。多项式平方和规划（Sum of Squares Programming,SOS规划）作为1种处理多项式形式非线性问题的新方法受到广泛关注。该方法由Jean首次提出并应用于单个多项式的平方和分解问题[5]。SOS规划是对LMI方法的补充，可应用于可行性问题和优化问题的求解中[6]。由于SOS规划在处理多项式形式非线性问题上的独特性，越来越多的LPV控制器设计问题转化为SOS规划问题，相应的SOSTOOLS也被开发出来，极大地推动了SOS规划在控制领域中的应用[7]。

将LPV控制应用于航空发动机全包线控制中，由于在包线内不同点发动机参数差别很大，单一的LPV控制器很难保证全包线内的控制效果[8]。因此，本文将飞行包线进行分区，分别对每个区域设计LPV控制器，然后结合切换系统相关理论保证切换时的稳定性。目前，众多学者展开了平滑过渡切换方法的研究。Song等[9]设计了1种基于平滑过渡切换的LPV鲁棒控制器，并将其应用于F-18战机中。江未来等[10]针对机翼后掠角可变飞行器控制问题，通过平滑过渡的方法进行切换LPV控制。

本文将平滑过渡切换应用于航空发动机全包线控制中，并通过SOS规划方法求解控制器。首先将飞行包线划分为奇数个子区域，分别建立每个子区域的LPV模型；然后给出闭环切换LPV系统鲁棒稳定的条件并将其转化为便于求解的SOS规划问题；最终在某型涡扇发动机上进行仿真验证。

1 航空发动机LPV模型

航空发动机非线性模型可以表示为

式中：x为发动机的状态变量；u为发动机的控制变量；y为发动机的输出变量。

选取高压转子转速为调度参数，根据非线性模型式（1）建立的发动机LPV模型

式中：x=[驻nL驻nH]T，驻nL、驻nH分别为风扇转速增量和高压转子转速增量；u=驻Wf，为发动机燃油流量增量；y=驻nH，为发动机高压转子转速增量。

式中：Nd为多项式阶次；[（nH）min（nH）max]为高压转子转速取值范围的最小值和最大值；θ为调度参数，变化范围为[0 1]。

最终，航空发动机状态变量LPV模型可写作

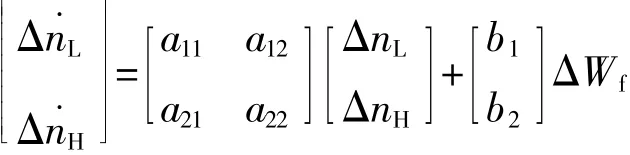
由式（2）～（5）可知，LPV模型的建立主要依据高压转子转速范围内不同稳态点系统矩阵的求解，而建立的LPV模型精度主要受多项式阶次Nd影响，Nd越大，LPV模型精度越高，但同时模型更加复杂，计算难度更大。

本文在保证模型精度满足要求的同时，为了不使计算过于复杂，选取Nd=3，以地面工作点（H=0 km，Ma=0）为例建立LPV模型，在高压转子转速变化范围（nH）min=0.86到（nH）min=1之间，每隔 nH=0.01选取 1个稳态工作点，稳态点对应的转速及其系统矩阵参数变化如图1所示。

图1 系统矩阵拟合

从图中可见，矩阵元素 a11、a12、a21在转速 nH=0.86、0.90、0.95时发生突变，这是由于发动机非线性部件级模型是依据转速特性图插值获得的，而nH=0.86、0.90、0.95均为插值端点，因此矩阵元素存在突变。拟合后得到LPV模型系统矩阵

为了检验所建立的LPV模型精度，分别在（H=0 km，Ma=0）、（H=10 km，Ma=1）2 个工作点任意选取 2个不同的高压转子转速，将LPV模型转化为线性模型，然后将线性模型与同一转速下的非线性模型分别作单位阶跃响应，其对比如图2、3所示。

图2 H=0 km、Ma=0处LPV模型与非线性模型阶跃响应对比

从图中可见，在不同高度、马赫数下LPV模型的阶跃响应与非线性模型的阶跃响应的拟合情况良好，稳态误差小于0.01%，说明设计的LPV模型在调度参数变化范围内能够精确地反映非线性模型动态响应的变化规律，因此该LPV模型能够满足建模精度要求。

针对上文所建立的LPV模型，设计状态反馈控制器，使转速闭环控制系统的高压转子转速可以较快地跟踪指令信号，同时H∞性能指标小于γ∞。考虑航空发动机存在外部扰动，则LPV系统为

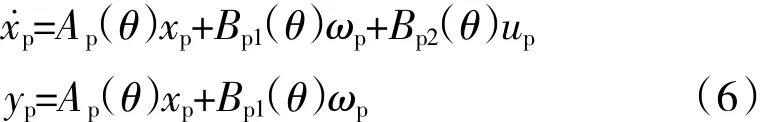
式中：xp、up、yp含义同式（2）中 x、u、y；ωp为外部扰动输入。

设控制指令为r，则输出偏差可表示为e=r-yp，偏差的积分xe=乙e d t，将偏差的积分增广为状态量以消除系统的稳态误差。得到广义被控对象的状态方程

针对系统（7），设计状态反馈控制律 u=K（θ）x，可得闭环状态空间方程

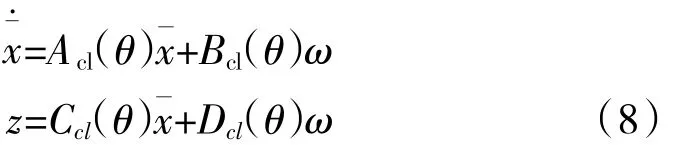
式中：Acl（θ）=A1（θ）+B2（θ）K（θ）；Bcl（θ）=B1（θ）；Ccl（θ）=C1（θ）；Dcl（θ）=D11（θ）。

2 切换LPV控制器设计

针对闭环LPV系统（8），采用Lyapunov函数保证各子系统的稳定性，同时根据LMI鲁棒稳定性条件及弱对偶定理将LPV控制器求解转换为SOS规划问题。

2.1 基于SOS规划的控制器设计

弱对偶定理[11]：考虑如下优化问题

式中：X为Rn的1个子集；f（x）、gi（x）为给定的关于x的函数，则f*≥q*，f*与q*的差值称为对偶间隙。

由弱对偶定理可知，如果存在s≥0使得L（x,s）≥0，则f*≥q*≥0。通过此定理可以将带约束的矩阵不等式条件转换为SOS规划问题，即将LMI的矩阵非负定条件转换为SOS的条件。

定理1[12]：对于系统（8），存在1个状态反馈H∞控制器，给定H∞性能指标γ∞＞0当且仅当存在1个实数对称矩阵X和实数矩阵W，使得下列不等式

成立，则 K（θ）=WX-1是系统（8）1个状态反馈控制器。N（θ）=A（θ）X+B2（θ）W+（A（θ）X+B2（θ）W）T。

定理1中Lyapunov矩阵不随调度参数变化而变化，虽然计算简单，易于处理，但保守性较大，很难求解出合适的控制器。

定理2：对于闭环系统（8），存在1个状态反馈H∞控制器，给定H∞性能指标γ∞＞0，如果存在SOS多项式矩阵 X（θ）、W（θ）、M（θ），使得下列多项式矩阵为SOS

则K（θ）=W（θ）X-1（θ）是1个能保证系统（7）稳定，且H∞性能指标为γ∞的状态反馈控制器。式中N（θ）=A（θ）X（θ）+B2（θ）W（θ）+（A（θ）X（θ）+B2（θ）W（θ））T。

2.2 包线区域划分

航空发动机的动态特性及状态空间模型均与进口条件有关[13]，对飞行包线进行划分时，首先应考虑划分后同一区域内发动机状态空间模型尽可能相似，使该区域内不同工作点均有良好的控制效果，可根据下式来量化包线内不同高度、马赫数下发动机性能差异

式中：T10、P10为标称点总温、总压；T1、P1为计算点的总温、总压；着为距离阈值，反映了子区域间不同工作点发动机动态性能的差异。

以（H=0 km，Ma=0）点为标称点，求取包线内所有工作点的 Γ 值，选取 着=0.25、0.50、0.75、1.00 将包线划分为6个区域，如图4所示，阴影区域为平滑过渡区。

2.3 平滑过渡切换LPV控制器

为缓解控制器间邦邦切换产生的抖振现象，提升切换时的控制效果，设计1种平滑切换LPV控制器。

考虑切换LPV系统闭环状态空间方程

式中：Acl,滓（θ）=A1,滓（θ）+B2,滓（θ）K滓（θ）；Bcl,滓（θ）=B1,滓（θ）；Ccl,滓（θ）=C1,滓（θ）；Dcl,滓（θ）=D11,滓（θ）；σ为系统的切换信号，其变化受高度和马赫数影响，由于高度和马赫数具有渐变特性，所以切换只发生在子区域边界处。

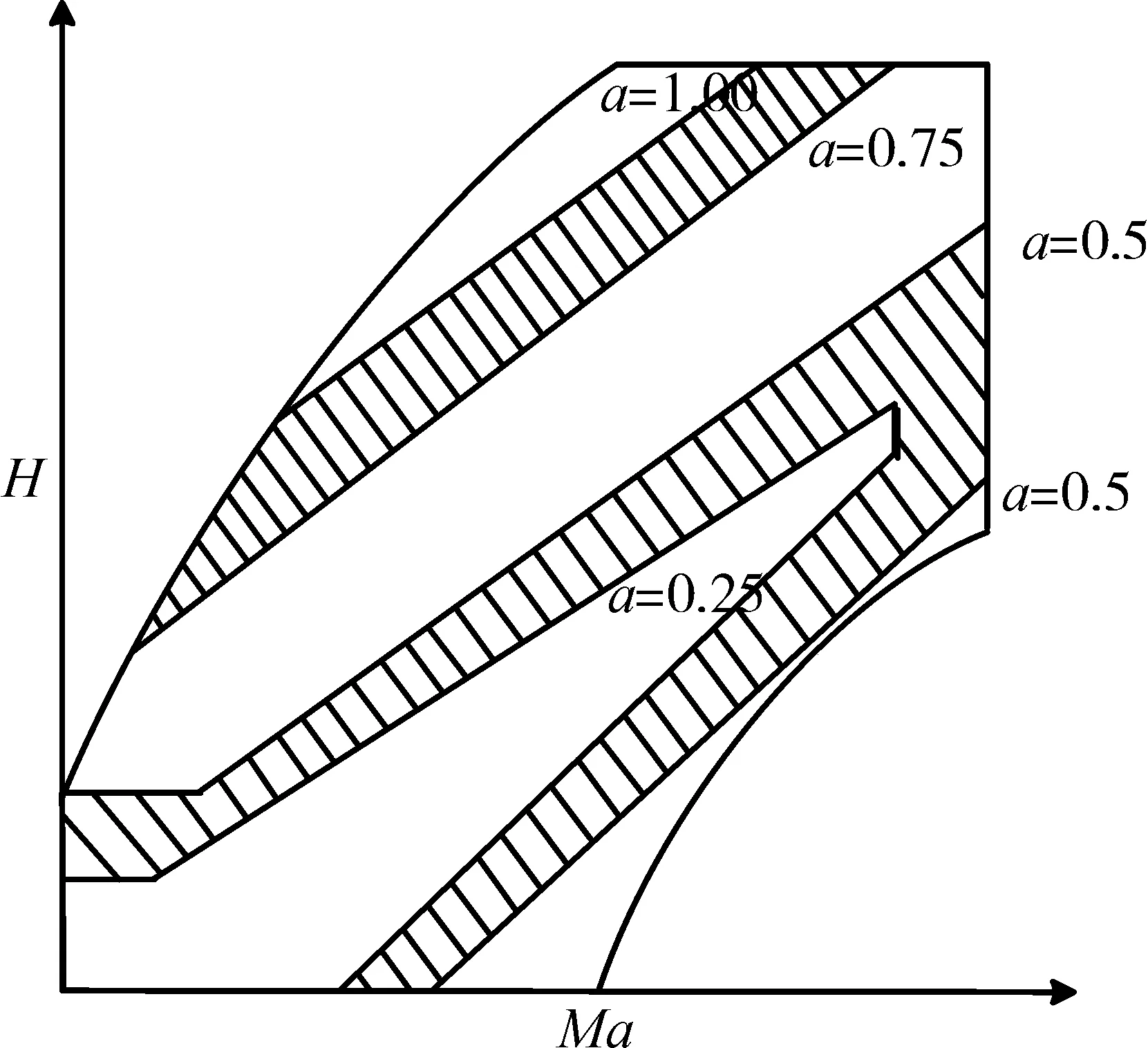
图4 包线区域划分

设 NJ={1，3，5，…，J} 为控制器求解区域，NO={2，4，6，…，J-1}为平滑过渡区域，其中 J表示包线内划分的子区域数目。当j∈NJ时，控制器为Kj（θ）；当j∈NO时，控制器为Kj-1,j+1（θ），由相邻2区域控制器Kj-1（θ）、K,j+1（θ）、插值获得。综上所述，全包线内的平滑过渡切换LPV控制器可表示为

其中Kj（θ）=Wj（θ）Xj（θ）-1，

Kj-1,j+1（θ）=Wj-1,j+1（θ）Xj-1,j+1（θ）-1，

Wj-1,j+1（θ）=CWj-1（θ）+（1-C）Wj+1（θ），

Xj-1,j+1（θ）=CXj-1（θ）+（1-C）Xj+1（θ）。

C为平滑切换系数，在此取

式中：ts为系统进入平滑过渡区域的时间。

定理3：针对航空发动机切换系统（14），存在1个状态反馈H肄控制器，给定H肄性能指标γ＞0，如果存在实数对称矩阵X（θ），实数矩阵W（θ）和SOS多项式矩阵Mj（θ），使得下列多项式矩阵为SOS

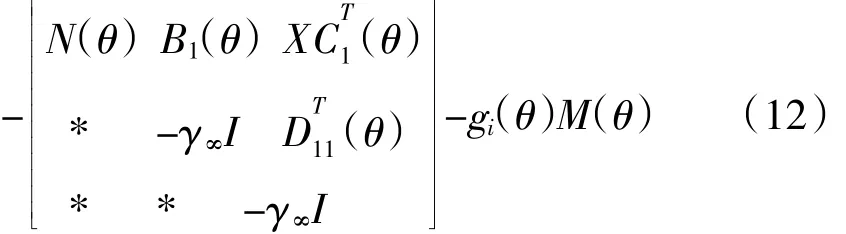
对任意j∈NJ均成立，则航空发动机闭环系统渐进稳定，且满足H肄性能指标γ肄。式中N（θ）=Aj（θ）X（θ）+B2,j（θ）W（θ）+（Aj（θ）X（θ）+B2,j（θ）W（θ））T。

证明：为方便阐述，选取飞行包线内相邻的3个区域 J1、J2、J3，其中 J2为平滑过渡区域，设

则根据定理3可得如下不等式

式中X1（θ）=X3（θ）=X（θ），采用式（15）中平滑切换系数，对式（18）中2不等式作线性叠加可得不等式

成立，则对于平滑过渡区域J2中任意一点，在相同的Lyapunov矩阵下,控制器K1（θ）、K3（θ）的任意线性叠加所获得的新控制器均可保证在区域J2内的系统稳定。

根据上述证明，能满足闭环LPV系统渐进稳定的控制器为K1（θ）、K3（θ），而对于区域J2，能满足闭环LPV系统渐进稳定的控制器为K1（θ）、K3（θ）及其任意的线性叠加，并且对于飞行包线内任意子系统有相同的Lyapunov矩阵使系统稳定，由此可知平滑过渡区域No内系统渐进稳定。

定理3中要求切换系统中所有的子区域都具有相同的多项式Lyapunov矩阵X（θ），显然，这种方式保守性大，当子区域数量过多的时候，很难找到1个合适的Lyapunov矩阵使所有子区域均满足控制要求。

对于切换LPV系统，假设存在1组正定矩阵{Xj（θ）}j沂NJ，每个矩阵可以保证在其对应的子区域J变化的连续性。则多参数依赖Lyapunov函数可写为

通过切换信号σ确定当前所处的子区域J以及对应的Lyapunov矩阵Xj（θ）。

一般而言，如果有合适的切换逻辑保证Vσ在其当前对应的子区域J内单调递减，则即使在整个参数轨迹上Vσ不是单调递减的，也可以保证切换LPV系统的稳定性[14]。

定理4：对于系统（14），存在1个状态反馈H∞控制器，给定H∞性能指标γ＞0，如果存在实数对称矩阵Xj（θ），实数矩阵W（θ）和SOS多项式矩阵Mj（θ），使得下列多项式矩阵为SOS

对任意j沂NJ均成立，则航空发动机闭环系统在飞行包线内渐进稳定，且满足H∞性能指标γ∞，K（jθ）=W（θ）X（θ）是保证系统（14）稳定，且 H∞性能指标为γ∞的状态反馈控制器。式中N（θ）=A（jθ）X（jθ）+B2（,jθ）W（θ）+（A（jθ）X（jθ）+B2（,jθ）W（θ））T。

证明：由于式（20）为SOS多项式矩阵，所以

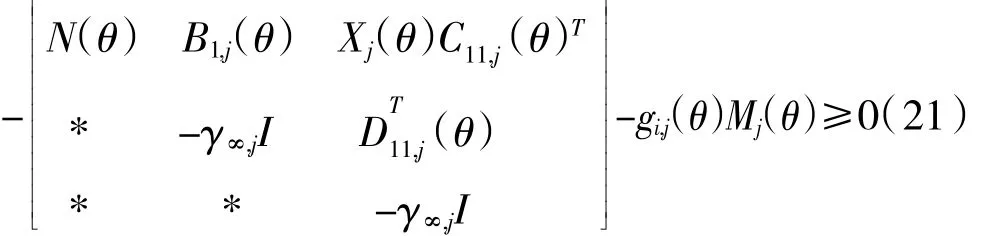
又知Mj（θ）为SOS矩阵，即Mj（θ）＞0，将弱对偶定理推广到多项式矩阵（21）中，可得

式（23）说明在θ∈专的整个区间内定理4均成立，即闭环切换系统（14）稳定且满足H∞性能指标γ∞。

根据定理4可知，系统（14）的控制器求解可以转化为SOS规划问题，控制器求解的具体步骤如下。

（1）对于非平滑过渡区，给定H∞性能指标γ∞，利用MATLAB中的SOSTOOLS工具箱分别求取每个子区域对应的SOS多项式矩阵Xj（θ）、W（θ）和Mj（θ），然后通过定理4求解出各子区域内满足要求的切换LPV控制器。

（2）对于平滑过渡区，采用式（15）中的平滑切换系数对相邻2个非平滑过渡区域的控制器进行插值，定理3中相关证明可保证平滑过渡区控制器的稳定性。

（3）将求得的切换LPV控制器在某型涡扇发动机上进行全包线仿真验证，相应的控制系统控制结构如图5所示。

3 仿真验证与分析

针对某型涡扇发动机在全包线内高度、马赫数和转速大范围渐进变化的情况，采用依据定理4设计的平滑切换LPV控制器进行闭环系统仿真验证。

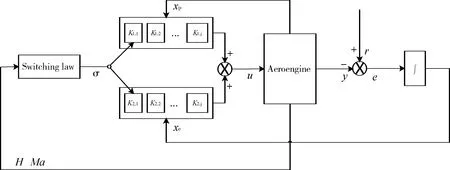
图5 全包线LPV切换控制系统结构

3.1 仿真分析1

在全包线内发动机高度、马赫数和转数的变化曲线如图6所示。从图中可见，在整个运行轨迹中共有4 次切换，分别是 16.5～18.75 s、24～26 s、37～39.5 s、43～47.5 s控制器经过平滑过渡切换区域。采用上述平滑过渡切换LPV控制器进行仿真验证，仿真结果（图6）切换区域局部放大如图7所示。

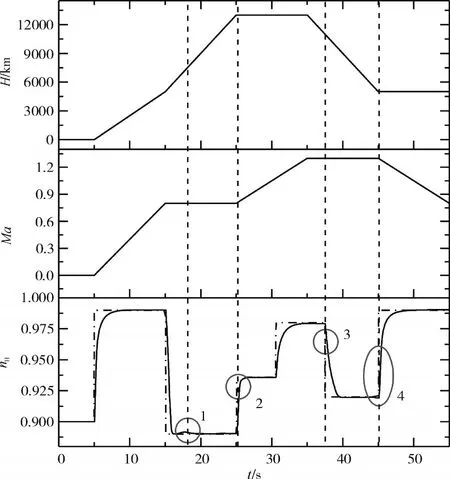
图6 飞行高度、马赫数和转速变化

图7 切换区域局部放大

从图6中可见，随着高度、马赫数的变化，高压转子转速可以很好地跟踪指令信号，响应时间约为3 s，且稳态误差小于0.5%，满足控制要求。

从图7可见，在上述4个切换区域中，控制器发生切换时，系统状态变化平稳，无跳变。

3.2 仿真分析2

对平滑过渡切换和邦邦切换方法作对比仿真验证，如图8所示。

从图中可见，采用邦邦切换时存在约3%的跳变，而平滑过渡切换很好地解决了这一问题。

3.3 仿真验证3

在全包线内选取11个多胞顶点，结合多胞理论设计全包线单一LPV控制器，与所设计的平滑过渡切换LPV控制器作对比。仿真结果如图9所示。

图8 切换方法对比

图9 控制方法对比

从图中可见，虽然单一LPV控制器不存在控制器间切换的跳变问题，但由于包线内不同工作点发动机性能参数存在较大差异，故相比于平滑切换LPV控制器跟踪响应更慢，且存在约4%的超调。

4 结论

本文针对航空发动机在全包线内转速大范围变化下的控制器设计问题，提出了1种基于SOS规划的平滑过渡切换LPV控制器。通过SOS规划的方法降低了传统LMI优化方法的保守性，同时采用平滑过渡切换解决邦邦切换时控制器存在的跳变问题。通过该方法设计的控制器可以精确跟踪指令信号，具有良好的鲁棒性，同时切换时不存在跳变，稳定性更强。