利用表象变换求解非厄米量子系统的能量本征值

高慧芬，周小芳

（长治学院 电子信息与物理系，山西 长治 046011）

初等量子力学中，我们的研究对象是本征值为实数的厄米系统。但是，本征值为实数的量子系统也可能是非厄米的。在非厄米系统中，通过调节系统参数，本征态可以合并，合并点称为奇异点。自1966年Kota提出奇异点概念以来，奇异点多次在实验上被验证和研究。例如，圆柱微波腔[1]、声学腔、光学腔[2][3]和耦合电子电路[4]等，这些系统中都可以观察到奇异点的存在。通过这些实验，许多由奇异点的产生而诱导的新奇现象得到了验证与研究，如超材料中的相干完美吸收[5]、损耗导致的复苏激光[2]等。

理论上，只要知道描写非厄米系统的哈密顿量，就可以求出系统的本征值，进而判断系统是否存在奇异点以及奇异点产生的条件。但是对于一个比较复杂的系统，只通过本征值而获得完整的奇异点的条件还是比较困难的。

文章介绍一种利用表象变换求解非厄米量子系统本征值的方法，该方法的优点是在求解本征值的同时，可以从不同的表象中看出奇异点是否存在，从而得到完整的奇异点条件。

1 非厄米系统本征值的计算

1.1 利用表象变换求解2×2非厄米系统的本征值

由两个耦合声学微腔A和B构成的二能级系统，哈密顿算符H可以写为：

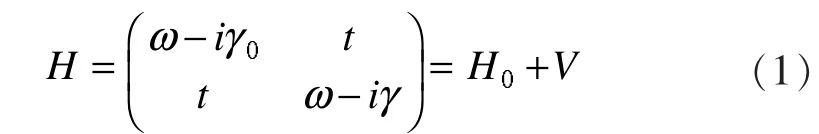
其中t是耦合系数，γ0是每个声学微腔的内部损耗，γ=γ0+Δγ，Δγ是两个微腔相互影响导致的损耗。将H写成

把H变换到H0表象

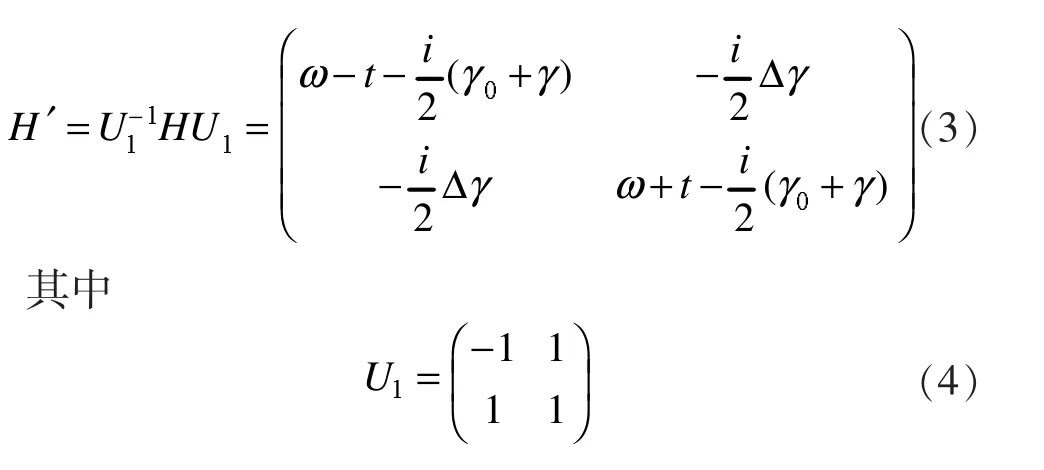
从（3）式可以看出，当 Δγ=0，t=0 时，H＇11=H＇22，此时存在奇异点。

为了求出系统存在奇异点的完整条件，将H＇再次对角化为：

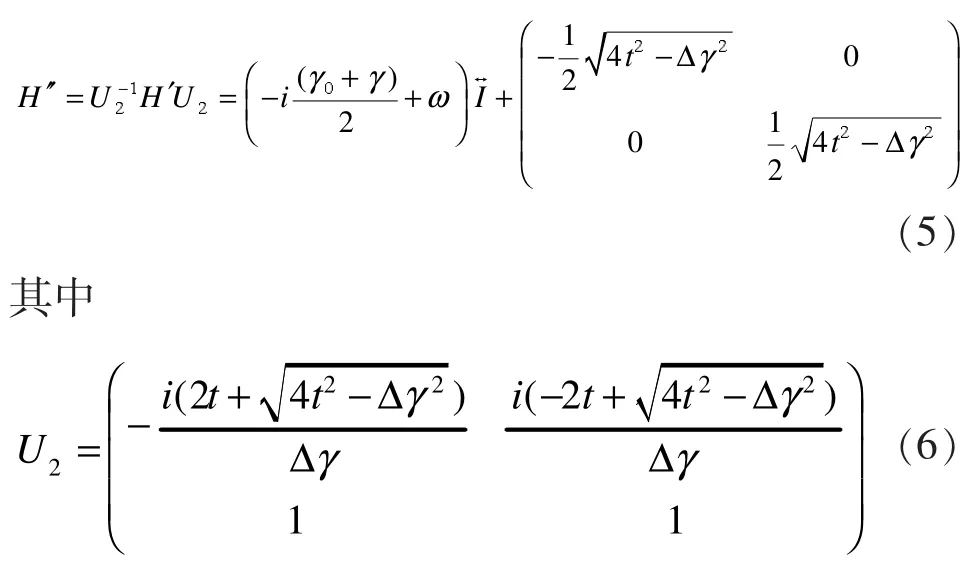
由（6）可知，系统的本征值为：

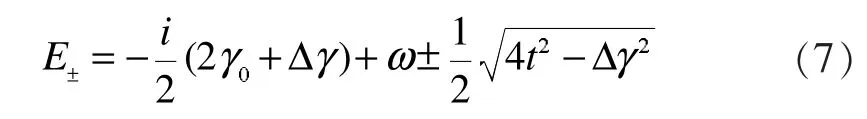
因此，系统奇异点存在的条件为：

1.2 利用表象变换求解4×4非厄米系统的本征值

由两对耦合声学微腔构成的四态系统，哈密顿量写为：

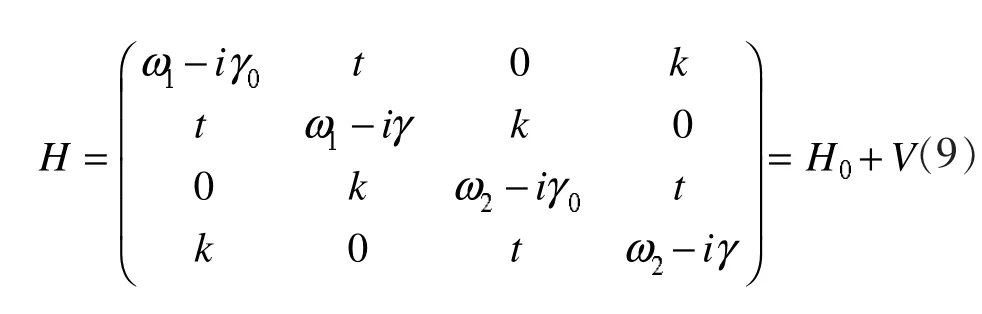
其中γ=γ0+Δγ，k是两对声学微腔之间的耦合系数，ω1和ω2是每对声学微腔的共振频率。将H写成

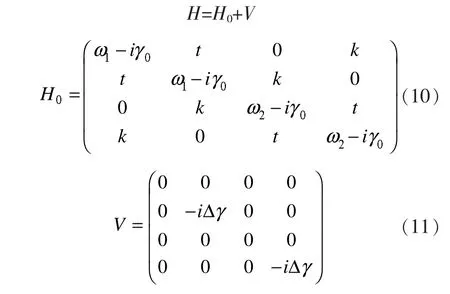
把H旋转到H0表象：

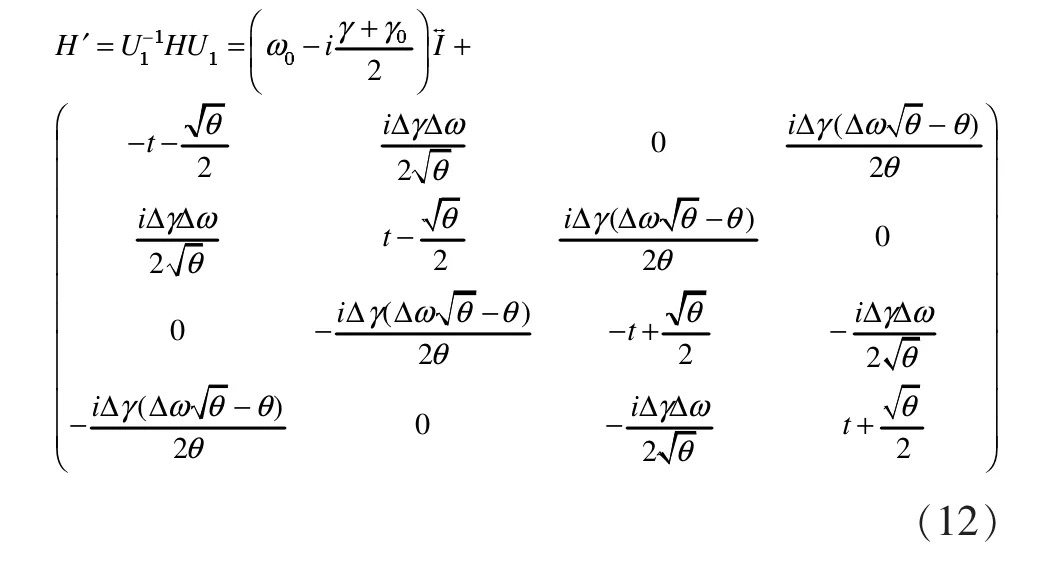
变换矩阵U1为：

为了求出系统存在奇异点的条件，将H＇再次对角化为：

由（15）可知，系统的本征值为：

因此，系统奇异点存在的条件为：

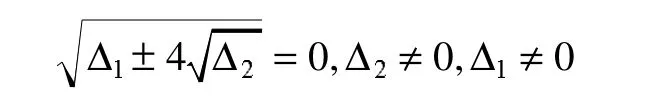
2 总结

文章利用表象变换求解了2×2和4×4非厄米量子系统的本征值。在求解过程中，利用量子系统在不同表象中本征值不变的性质，在定性理解一些奇异点出现的物理本质的同时，求出了奇异点满足的完整条件。由于该方法涉及到系统哈密顿量在不同表象中的表示形式，从各种表示形式中可以看出一些奇异点出现的条件，因此，该方法在处理更高阶的非厄米量子系统时，得到的奇异点条件更完整。