A企业汽车混流装配线排产研究

庞博高雅 王 巍

(东北林业大学工程技术学院，黑龙江 哈尔滨 150040)

1 混流装配线

1.1 混流装配线及其特征

多品种混合装配线实际是一个柔性生产线，亦可在同一产线上同时装配多个不同的品种。它是在数量均衡和品种均衡基础上，以日产量和不同型号比例为依据，对产线上多种型号产品进行有序合理的排序，将多种不同型号的产品在同一产线上进行装配。

多品种混合装配线的特征如下:

1)在同一条产线上可以装配统一系列不同型号的成品。

2)产品连续混合的进行装配，而并非大量生产。

3)在制品库存数量能适当降低。

4)混流装配线上成品的外观和大小虽然存在差异，但大都具有类似的工艺流程。

5)在转换生产不同型号产品时，基本无需调换产线。

1.2 混流装配线排序问题

眼下本国大规模制造企业主要采取的生产模式是JIT生产方式，它应用混流生产线来生产。几乎不改变已有生产手法、生产前提和生产能力，而是通过改变生产组织方式，在特定时间内，使多种差异型号、差异数量的成品在同一条产线上生产出来[1]。企业为了能够实现准时化的生产目标，常常将目光放在物料需求的波动上，即准时化生产的目标就是使物料消耗速率保持均衡，以保证物料需求的稳定性[2]。不同型号的产品需要不同类型及数量的零部件和原材料，所以产品装配序列很大程度上影响物料供应的均衡性。

现在，混流生产线在汽车、手机、家电等行业应用的已经相当广泛。这些制造类企业的产品一般只是型号和规格的不同，功能和作业方式基本一致。所以，在装配生产过程中，生产不同型号的产品时产线通常不用做出调整，此类产品更新较快，要跟随顾客需求的变化而变化，在最短的时间里，最大程度地适应不同消费者的差异需求。从而混流生产线快速回应市场需求变革，增加成品和企业的竞争力。

混流产线的组织形式比较先进。而协调多品种混流生产的主导问题是落实生产的“平准化”，其第一要义是不同型号的产品在混流生产线上排产序列的最优化。即:事先要人为的按照加工时间、数目、品种进行合理搭配和排序，而后将成品拉动到生产战线，使加工时间能够平稳，生产可以均衡，同时在品种和数目上真正达到混流的效果，能够对市场的多样个性需求做出及时、迅速的反应。那么对混流产线排产问题的研究讨论，一定会将JIT生产方式的优点发挥的很好。

使汽车出产顺利进行的前提是彻底贯彻生产均衡与同步，也就是落实平准化的JIT生产方式，这里的平准化不仅包含汽车成品生产均衡，还包括它的前面的那一道工序零件生产的均衡。为了实现这种均衡，应该找到一种使得物料的现实损耗快慢与理想损耗快慢差距很小的排产方案[3]。

目前用于混流装配线排产研究的优化目标有很多种，其中均衡装配线上各零件消耗速率这一优化目标的实质是实现物流的平准化，该目标更容易解决企业的实际问题，且更容易为企业带来实际生产效益[4]。因此，大多数企业建立混流装配线时采用均衡装配线上各零件消耗速率目标的优化模型。

为了使得各个零部件的使用速率保持均衡，需要统计一个生产循环内进行排产的各车辆所需每种零部件的数量，计算装配一辆汽车所需某零部件数量作为理想使用率，对某零部件的实际使用情况作为实际使用率。本文的目标是使零件理想使用率与现实使用率的差距最小。为了促成此目标，丰田公司创设了目标追随法。正文以A汽车制造企业为例，进行侧重研究。

2 A企业现状及混流装配线数学模型的建立

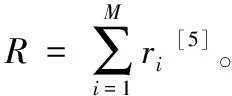
2.1 A企业现状

本例中，A汽车制造企业为响应复杂多样的市场需求，引进混流装配生产线，本文为方便描述将该产线的车型分别记为：A,B,C,D，已知该企业确定某日的计划生产量为：A型车400辆，B型车300辆，C型车200辆，D型车300辆。确定好一个计划期的预计产量后，根据最小生产循环的方法，得到一个生产循环内四种不同车型的需求比为：4∶3∶2∶3，所以在一个生产循环中可以生产A车型4辆，B车型3辆，C车型2辆，D车型3辆，见表1。

目前，A企业在一个生产循环中，产品投放顺序按照D-D-D-A-A-A-A-B-B-B-C-C进行，则工作站上装配零件3的人员须要从一个生产循环的起始即连续装配45件零件3，此时对零件3的物流需求急剧增加；紧接着由于A车型上不需要装配零件3，因此对零件3的物流需求降低；同样地，如果投放顺序改为A-A-A-A-D-D-D-B-B-B-C-C，则工作站在开始的很长一段时间内都没有对零件3的物流需求，然后再连续装配45件零件3，又急剧增加了物流需求量。由于不同产品投放次序不合理，造成了工作站物料流动不均衡的现象[6]。

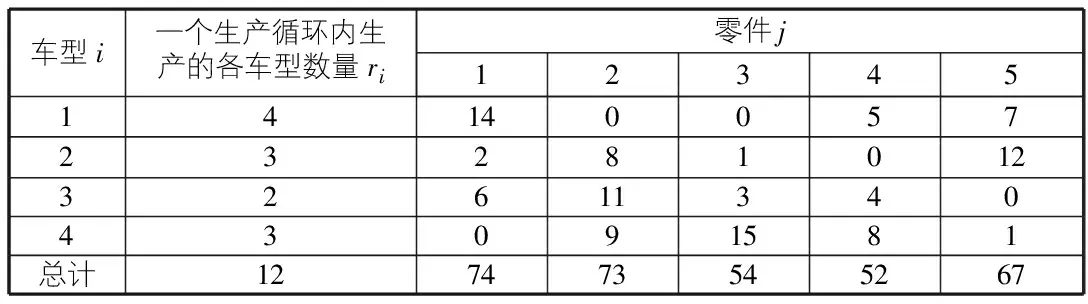
表1 各车型数量及主要零件清单

2.2 汽车混流装配线数学模型的建立

为了解决这种忙碌和空闲不均匀的矛盾，同时也为降低在制品的储存量，推进准时化生产的顺利进行。总装线在组装所有车辆的过程中，投产顺序应遵循各零部件使用速率均衡化的原则，即必须尽量使各个零部件的实际使用率和理想使用率之差最小化。在此理论基础上建立混流生产线投产顺序数学模型如下[3]：

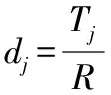
约束条件为：

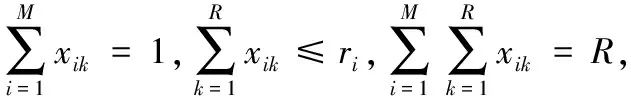
约束条件分别表明：排产顺序的前k个位置，每一个位置最多只得装配一辆车；参与排序的车型i的数目不超出一个生产循环内该车型的需求总量；一个生产循环内投产排序的车辆数为R。

3 目标追随法在A企业总装配线排产研究

根据上文建立的混流装配线投产排序的数学模型，结合A汽车制造企业某天的生产计划可以得到如下数学模型。

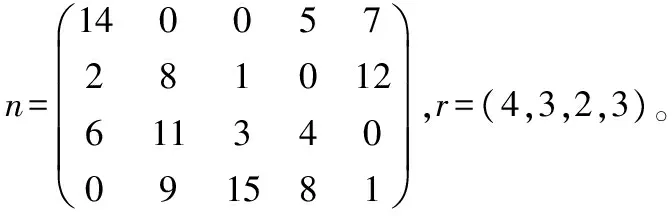
目标函数：

可变形为：

(1)

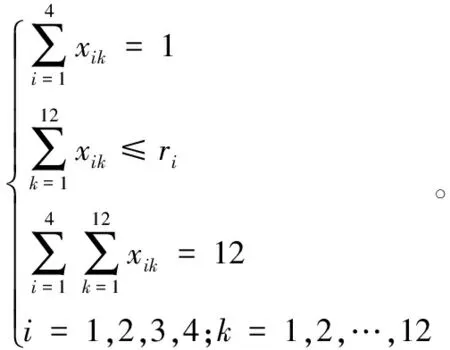
应用目标追随法求解所建立的A汽车制造企业装配线投产排序的数学模型。

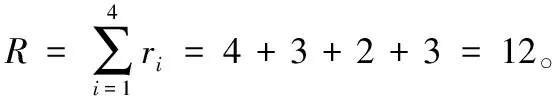
当k=1时，

对于i=1时，

D1,1=(1×74/12-0-14)2+(1×73/12-0-0)2+(1×54/12-0-0)2+(1×52/12-0-5)2+(1×67/12-0-7)2=121.069；

对于i=2时，

D1,2=(1×74/12-0-2)2+(1×73/12-0-8)2+(1×54/12-0-1)2+(1×52/12-0-0)2+(1×67/12-0-12)2=93.236；

对于i=3时，

D1,3=(1×74/12-0-6)2+(1×73/12-0-11)2+(1×54/12-0-3)2+(1×52/12-0-4)2+(1×67/12-0-0)2=57.736；

对于i=4时，

D1,4=(1×74/12-0-0)2+(1×73/12-0-9)2+(1×54/12-0-15)2+(1×52/12-0-8)2+(1×67/12-0-1)2=191.236；

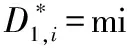
即i*=3时，在最小生产循环内的首位所应排序的车型为C车型。

将i=3代入vj,k=vj,k-1+n3,j。

当k=1时，

v1,1=v1,0+n3,1=0+6=6;

v2,1=v2,0+n3,2=0+11=11;

v3,1=v3,0+n3,3=0+3=3;

v4,1=v4,0+n3,4=0+4=4;

v5,1=v5,0+n3,5=0+0=0。

同理，按照目标追随法的步骤计算，即能够得到一个生产循环内各车型车辆的投产排序结果如表2所示。

可知排产结果为：321412413241。

对应的投产顺序车型为：

CBADABDACBDA。

最后，求得目标函数值为：

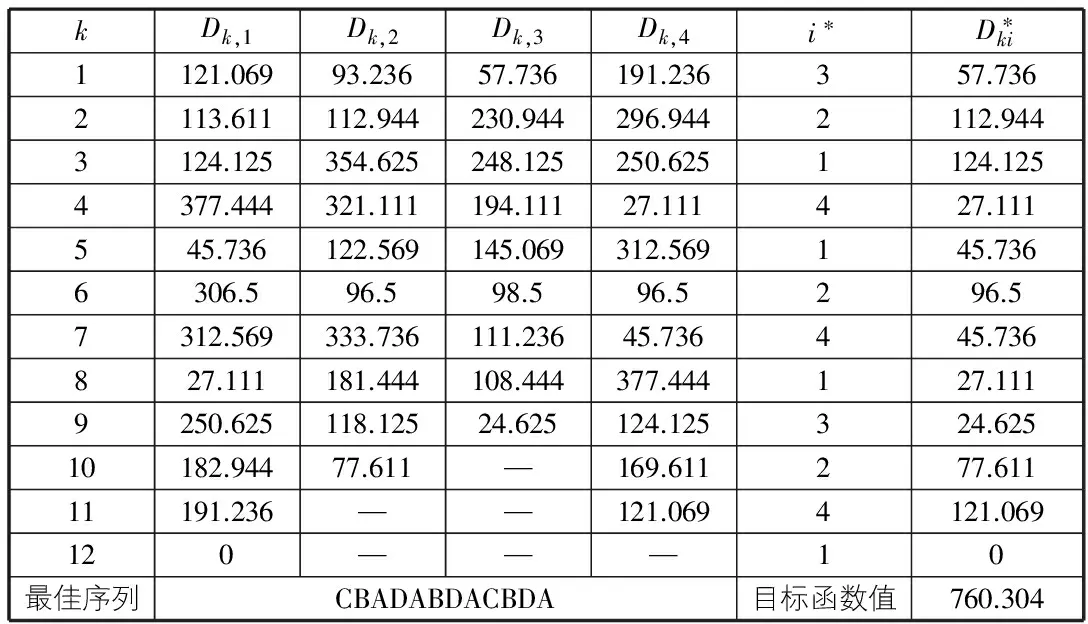
表2 A汽车制造企业某天的投产排序计划表

4 结果及讨论

以A汽车制造企业为例，建立了混流装配线投产排序的数学模型，应用目标追随法求解排产模型。得到该企业某天的装配线进行投产的顺序为CBADABDACBDA。但应用目标追随法仍存在一些问题：如求解的时间比较长、所求解并不是全局最优解，在今后应研究比较不同方法在解决此类问题上的时间及效率，进而得到全局最优解，为企业生产带来更多的参考与借鉴。

[1] 韩丽莎.混流装配线投产排序优化设计[D].大连：大连理工大学,2012.

[2] 刘兆惠.JIT生产方式混流生产线投产排序研究[D].长春：吉林大学,2004.

[3] 王 巍,王 静.基于JIT的汽车混流装配线排产研究[J].森林工程,2014,30(4):167-171.

[4] 赵慧真.摩托车混流装配线投产顺序研究[D].重庆：重庆理工大学,2015.

[5] 李仕福.基于遗传算法的混流装配线投产排序问题研究[D].长春：吉林大学,2015.

[6] 刘文平.混合品种汽车装配线平衡与排序问题研究[D].济南：山东大学,2009.