7075铝合金二维超声挤压加工的灰色关联分析

郑建新 任元超

(河南理工大学机械与动力工程学院，焦作 454003)

0 引言

7075铝合金由于具有比强度高、断裂韧性好等优点，在航空航天和兵器工业中得到广泛应用。由于其服役环境严苛，常因疲劳、磨损和腐蚀等问题引起过早失效[1]。零件的失效大多从表层开始，为提高7075铝合金零件的服役寿命，在零件制造时应设法提高其表面质量，如降低表面粗糙度值，提高表层显微硬度，并在表层形成适度的残余压应力等。

超声表面强化工艺是基于传统的表面机械强化工艺，如喷丸、挤压和滚压等，通过对工具施加纵向超声振动，对零件表面进行超声频撞击而强化零件表面[2-5]。R.Ramos等人[6]对7475-T7351铝合金超声喷丸处理与普通喷丸处理进行对比，发现超声喷丸处理可以降低表面粗糙度、提高表层硬度、增加疲劳寿命。郑建新等人[7]对6061-T6铝合金进行超声深滚处理，结果表明超声深滚加工可明显降低表面粗糙度，大幅增加表面显微硬度。张勤俭等人[8]进行超声挤压30CrMoA车轴钢试验，试验发现超声挤压加工可提高金属材料的疲劳强度和使用寿命。

超声强化后零件的表面质量由多个指标来综合衡量，而这些性能指标又受约于多个加工工艺参数。如何选择合理的加工方案使多个评价指标达到最优，是工程应用中必须考虑的问题。

为了解决多目标优化的难题，给决策提供科学的依据与方法，邓聚龙教授于1982年提出了灰色系统理论和灰色关联分析法(GRA)[9]，在多目标响应方面得到了广泛运用[10-11]。

本文将采用正交试验法对7075-T651铝合金进行二维超声挤压加工试验，运用灰色关联分析法对试验结果进行综合评定，研究各加工工艺参数对表面粗糙度和显微硬度的综合影响，优选工艺方案并建立灰色关联度数学模型，以供生产应用。

1 试验设计

1.1 试验材料及设备

在CAK50186di数控车床上将自主研制的单激励纵弯复合振动二维超声振动挤压加工声学系统安装在车床刀架上，加工原理如图1所示。超声振动声学系统的谐振频率为20.6 kHz，工具头纵向振动振幅L=9.6 μm，横向振动振幅T=4.9 μm。

图1 加工原理示意图

材料为供应态7075-T651铝合金棒料，化学成分如表1所示。

表1 7075-T651化学成分

7075-T651铝合金棒料直径为Ф90 mm，长度为20 mm。每次试验前先对棒料端面在相同切削用量下进行端面车削，然后进行二维超声挤压加工试验。

采用SURTRONIC3+粗糙度测量仪测量试件表面粗糙度Ra值；采用配备DL探头的TH160便携式硬度测试仪测试试件里氏硬度HL值。在被加工表面上均布选取7个测试点，测试用竖直冲击方式，测试值取7个测试点的均值。经车削后试件表面粗糙度Ra测试值约为1.72 μm，显微硬度约为512 HL。

1.2 试验方案及结果

主要研究在二维超声挤压加工中静压力Fs、进给量fr和挤压速度v三个挤压工艺参数对试件加工后的表面粗糙度Ra值和表层显微硬度HL值的影响。每个因素各安排三个水平，选用正交表L9(34)安排试验，试验方案和结果如表2所示。

表2表明，经二维超声挤压后，7075-T651铝合金表面粗糙度值显著降低，而表层显微硬度大幅提高。

表2 试验方案与结果

2 灰色关联分析

2.1 灰色关联度计算

由于试验结果不具有相同的增减性，需要对试验结果进行信噪比计算，计算后的结果越大表示相应质量越好。

计算表面粗糙度Ra的信噪比和显微硬度HL的信噪比S/N分别选用式(1)和式(2)[12]。计算结果如表3所示。

(1)

(2)

式中，Xi表示第i组试验获得的表面粗糙度Ra值；Yi表示第i组试验获得的显微硬度HL值。

经信噪比处理后的结果量纲不同，不能直接进行灰色关联度分析，故需要使用式(3)[12]将其标准化。计算结果如表3所示。

(3)

式中，xij表示第j个标准的第i个试验信噪比值的标准化值，yij表示第j个标准的第i个试验信噪比S/N的值；这里i=1～9，j=1～2。

计算灰色关联度(GRD)γj前必须先计算灰色关联系数εij，εij采用式(4)[13]进行计算。计算结果如表3所示。

(4)

式中，xi0为参照数，一般取最优组，这里取xi0=1；ξ为分辨系数，ξ∈[0，1]，其取值可根据下列计算：

(5)

式中，m表示试验组数，m=9；n表示评价标准个数，n=2；Δ表示差值绝对值的均值。

由式(5)知，Δ=0.493。

由于2<1/Δ<3，故ξ=2Δ=0.986[14]。

使用式(6)进行灰色关联度γj计算，结果如表3所示。

(6)

表3 灰色关联度分析结果

灰色关联度反映了工艺参数对零部件表面质量综合影响的好坏，其值越大表示表面质量越好。对灰色关联度进行排序可知，第2组灰色关联度值最大，说明它是这9组试验中最佳的参数优化组合，即获得最佳表面质量的工艺参数为：Fs=220 N，v=50 m/min，fr=0.1 mm/r。

2.2 各工艺参数对加工质量的影响

基于试验结果可分析工艺参数对加工质量的影响。结合表2和表3，确定表面粗糙度、显微硬度和灰色关联度的极差分析结果，如表4～表6所示。

表4表明，挤压速度对表面粗糙度的影响最大，其次是静压力，进给量的影响最小。获得最小表面粗糙度值时的工艺参数为：Fs=300 N，v=30 m/min，fr=0.06 mm/r。表5表明，挤压速度对显微硬度的影响最大，其次是进给量，静压力与进给量的影响较接近。获得最高显微硬度值时的工艺参数为：Fs=220 N，v=70 m/min，fr=0.1 mm/r。表6表明，进给量对灰色关联度的影响最大，其次是挤压速度和进给量，且两者较为接近。获得最大灰色关联度时的工艺参数为：Fs=260 N，v=50 m/min，fr=0.1 mm/r。

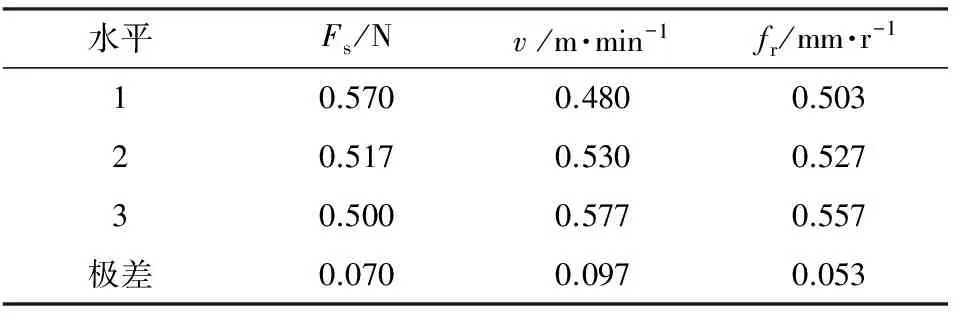
表4 表面粗糙度极差分析

表5 显微硬度极差分析

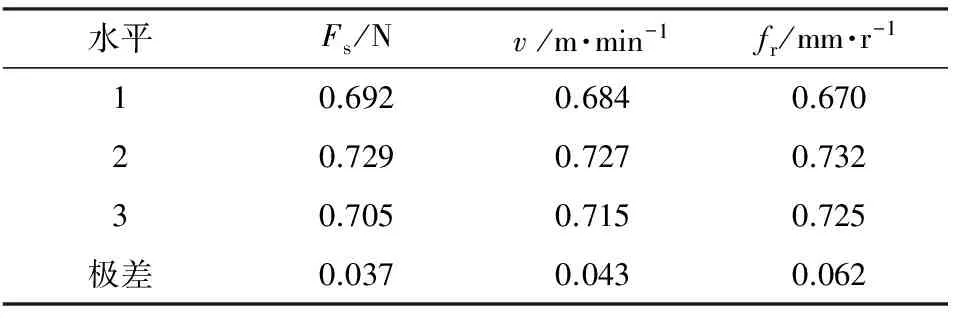
表6 灰色关联度度极差分析

基于表4～表6进一步分析静压力、挤压速度和进给量对表面粗糙度、显微硬度和灰色关联度的影响，其主效应如图2所示。图2直观表明，表面粗糙度值随静压力的增大逐渐减小，而随着挤压速度和进给量的增大逐渐增大；显微硬度值随着静压力的增大逐渐减小，随着挤压速度的增大逐渐增大，随着进给量的增大先增后减；灰色关联度随着静压力、挤压速度和进给量的增大先增后减。

显然，各工艺参数对表面粗糙度、显微硬度和灰色关联度的影响规律不同，同时各工艺参数之间可能存在的交互作用，从而导致获得最小表面粗糙度值和最高显微硬度值的最优工艺参数各不相同，获得最大灰色关联度的最优工艺参数也发生变化。

已有研究从物理力学角度探讨了超声强化加工工艺参数对表面粗糙度和显微硬度的影响[6-8]，此处不再赘述。

(a) 静压力的影响

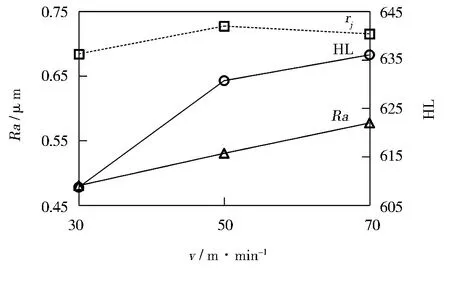
(b) 挤压速度的影响

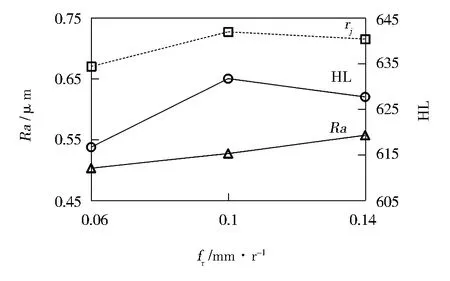
(c) 进给速度的影响

3 灰色关联度预测

本文研究获取最优工艺参数，以获得最佳的综合表面质量，即最小的表面粗糙度值和最高的显微硬度值。以上分析表明，基于灰色关联度计算获得的最优工艺参数与利用极差分析获得的最优工艺参数并不一致。为此，基于表2～表3数据采用多元线性回归模型构建灰色关联度预测模型。

定义：Fs=x1，v=x2，fr=x3，γj=f(x1,x2,x3)，则获得γj预测模型如式(7)所示。

γj=-1.017+0.02x2+28.5x3-0.00004821x1x2-

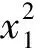
(7)

基于式(7)获得的灰色关联度预测值与基于表3获得的计算值基本一致，最大误差不超过3%，该预测模型在Fs= 220～300 N、v=30～70 m/min和fr=0.06～0.14 mm/r范围可对灰色关联度进行有效预测。

基于式(7)对灰色关联度在Fs=220～300 N、v=30～70 m/min和fr=0.06～0.14 mm/r范围内进行非线性规划求解，设置初值为[300 70 0.14]，经迭代计算后所得解为[220 30 0.14]，此时可获得最大灰色关联度值γj=0.946，远大于表3中各组试验得到的最大关联度值。

进一步进行工艺试验，当Fs=220 N，v=30 m/min，fr=0.14 mm/r时获得的表面粗糙度Ra约为0.44 μm，比第2组试验获得的最小表面粗糙度值降低了13.73%；显微硬度约为637 HL，比第2组试验获得的最大显微硬度值降低了0.47%。在该工艺参数下，显微硬度基本不变，而表面粗糙度值显著降低，因而可认为基于灰色关联度预测模型进行规划求解获得的最优工艺参数是工艺参数范围内的最优解。

4 结论

对7075-T651铝合金二维超声挤压加工后，试验结果表明：

(1)表面粗糙度值随静压力的增大逐渐减小，而随着挤压速度和进给量的增大逐渐增大。

(2)显微硬度值随着静压力的增大逐渐减小，随着挤压速度的增大逐渐增大，随着进给量的增大先增后减。

(3)表面质量随着静压力、挤压速度和进给量的增大先增后减。

(4)采用多元线性回归模型构建的二维超声挤压加工灰色关联度预测模型可对试验进行有效预测。

(5)基于灰色关联度预测模型进行规划求解获得了最优工艺参数，即Fs=220 N，v=30 m/min，fr=0.14 mm/r，此时表面粗糙度Ra约为0.44 μm，显微硬度约为637 HL。

[1] RYL J, WYSOCKA J, JARZYNKA M, et al. Effect of native air-formed oxidation on the corrosion behavior of AA 7075 aluminum alloys [J]. Corrosion Science, 2014, 87(5):150-155.

[2] 郑建新, 罗傲梅, 刘传绍. 超声表面强化技术的研究进展[J]. 制造技术与机床, 2012(10):32-36.

[3] ZHANG Q, CAO J, WANG H. Ultrasonic surface strengthening of train axle material 30CrMoA [J]. Procedia Cirp, 2016, 42:853-857.

[4] VASYLYEV M A, CHENAKIN S P, YATSENKO L F. Ultrasonic impact treatment induced oxidation of Ti6Al4V alloy [J]. Acta Materialia, 2016, 103:761-774.

[5] CHENG M, ZHANG D, CHEN H, et al. Development of ultrasonic thread root rolling technology for prolonging the fatigue performance of high strength thread [J]. Journal of Materials Processing Tech., 2014, 214(11):2395-2401.

[6] RAMOS R, FERREIRA N, FERREIRA J A M, et al. Improvement in fatigue life of Al 7475-T7351 alloy specimens by applying ultrasonic and microshot peening [J]. International Journal of Fatigue, 2016, 92:87-95.

[7] 郑建新, 罗傲梅. 6061-T6铝合金纵-扭复合振动超声深滚加工试验研究[J]. 稀有金属材料与工程, 2015, 44(3):733-737.

[8] 张勤俭, 王会英, 刘月明, 等. 30CrMoA车轴材料超声表面挤压强化技术研究[J]. 应用基础与工程科学学报, 2015(s1):177-184.

[9] DENG J L. Control problems of grey systems [J]. Systems & Control Letters, 1982, 1(5): 288-294.

[10] DHARMALINGAM S, SUBRAMANIAN R, KOK M. Optimization of abrasive wear performance in aluminium hybrid metal matrix composites using taguchi-grey relational analysis [J]. Proceedings of the Institution of Mechanical Engineers Part J Journal of Engineering Tribology, 2013, 227(7):749-760.

[11] OTIM F J, CHOI S J. Influence of cutting parameters on energy consumption and material removal rate in turning process [J]. Applied Mechanics & Materials, 2015, 799-800: 282-290.

[12] 刘春景, 唐敦兵, 何华, 等. 基于灰色关联和主成分分析的车削加工多目标优化[J]. 农业机械学报, 2013, 44(4):293-298.

[13] 贾振元, 顾丰, 王福吉,等. 基于信噪比与灰关联度的电火花微小孔加工工艺参数的优化[J]. 机械工程学报, 2007, 43(7):63-67.

[14] 东亚斌, 段志善. 灰色关联度分辨系数的一种新的确定方法[J]. 西安建筑科技大学学报(自然科学版), 2008, 40(4):589-592.