面向空间站桁架的三分支机器人的步态规划与研究
赵京东,韩均广,倪风雷,赵亮亮,刘 宏
(哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨150080)
1 引言
最早出现的执行空间站复杂操作任务的攀爬机器人是20世纪90年代早期美国卡内基梅隆大学研制的七自由度 SM2[1⁃2]。 其本体为串联操作臂,两端配以抓夹工字梁的三指夹持器。最为经典的是加拿大研制的空间舱外机器人服务系统SS⁃MSS[3]。 其典型特征为机械臂的两端均安装有可以固定到空间站专用锁紧位置上的锁紧装置,在空间站进行在轨服务时,该机械臂可以通过变换锁紧位置,实现在空间站上的攀爬行走。虽然它可以通过“端头效应器”实现在舱外的行走,但由于其为体积庞大的单链式结构,不能适应空间站舱内狭小空间的操作需求。
在2011年美国成功发射升空了多臂仿人机器人系统R2,在2014年美国宇航局为在空间站工作的R2安装了两条腿,每个分支均具有7个自由度,分支的末端带有夹持器,可以使机器人实现攀爬运动[4]。R2机器人仍属于二分支攀爬机器人,在攀爬的速度以及复杂任务的操作上存在很多不足。
研究机器人的攀爬方式对空间机器人作业具有较大的帮助。在国外,日本早稻田大学在2005年爱知国际博览会展出了爬树机器人原型机WOODY⁃1,西班牙马德里卡洛斯三世大学开发出了基于并联机器人的爬树机器人CPR[5];英国威尔士大学研制了电磁吸附式攀爬机器人,但这种仅有两个自由度的机器人无越障能力[6]。以色列KCG实验室研制的具有8个自由度的攀爬机器人可以实现越障功能,但负载能力较差[7]。剑桥大学在2013年提出了针对冗余自由度的二分支攀爬机器人的避障的运动步态[8]。
在国内,广东工业大学管贻生教授设计了一种通过不同关节模块和夹持模块的组合,实现在空间桁架结构中移动的可重构模块化机器人,并提出了二分支攀爬机器人的尺蠖步态及翻滚步态[9⁃10]。这两种步态在移动时全部的分支都参与移动,翻滚步态中部分关节的摆动角度过大,对机器人攀爬过程中的移动速度有较大影响。
采用三分支机器人可以较好的解决这些问题。本文提出采用9个单自由度的关节模块连接组成三分支机器人的本体,其中9个关节轴和杆件轴垂直的摆动关节模块在中间,其关节轴线相互平行,三个夹持器分布在末端位置,组成了中心对称的三分支攀爬机器人。其中夹持器既可以夹持物体又可以夹持在空间站中的桁架杆件上。由于具有较多的自由度,三分支机器人具有更多的运动方式,同时具有一个独立的运动分支用以完成复杂任务。其机构及简化模型的运动学模型示意图如图1所示。

图1 三分支机器人运动学模型Fig.1 Kinematic model of the climbing robot with three branches
2 三分支机器人位姿运动学正运算
目前广泛应用的机器人运动学模型是D⁃H模型。机器人关节坐标可描述机器人各杆件和终端之间的运动,是建立运动学方程的基础性工作。根据D⁃H法则对机器人进行正运动学分析需要先确定出机器人的D⁃H参数,包括关节轴之间的夹角α、连杆长度a、连杆偏距d和关节转角θ。D⁃H坐标如图1所示,在机器人中,坐标系Oi所在位置的关节定义为Ti,机器人的每一段杆长设为l。由于三分支机器人具有三个分支,因此在正运动学的位置分析时建立两个独立的 D⁃H 模型,分别为 i=0、1、2、3、4、5、6、7 时和 i=0、1、2、3、4′、5′、6′、7′时的模型,D⁃H参数表如表1所示。在三分支的机器人的两个D⁃H模型通过解析法进行运动学正运算可得式(1) ~(3):
i=0、1、2、3、4、5、6、7 时,
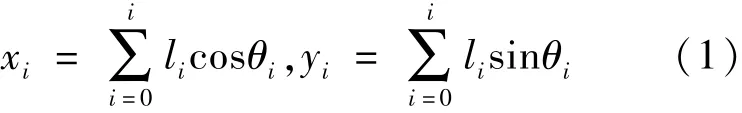
i=0、1、2、3、4′、5′、6′、7′时,

3 三种步态规划及运动学逆运算
三分支机器人根据其具有9个自由度并且关节轴线相互平行的构型特点,在桁架杆件上攀爬时可以采用3种不同的步态,分别是两个分支参与运动的尺蠖步态、速度较快的翻滚步态一和至少有两个夹持器处于夹持状态的翻滚步态二。
3.1 尺蠖步态
第一种步态为尺蠖步态,具有一个独立的分支,可以用于进行高度不超过5l的狭小空间的操作和移动过程中载荷的搬运,如图2所示。
其攀爬步骤如下:
1)机器人处于初始位置,上下两个夹持器均处于夹紧状态,左侧分支的末端夹持器慢慢张开,右侧分支的末端夹持器保持夹紧,支撑机器人;
2)T1、T2、T3、T4、T5、T6六个关节协调转动,机器人躯体收缩。T1和T6转过α角的时候,T3和T、T和T应协调转过角;
3)当摆动关节完成转动后,左侧分支的末端夹持器开始闭合至夹紧杆件,然后右侧分支的末端夹持器慢慢张开,机器人由左侧分支的末端夹持器单独支撑;
4)摆动关节 T1、T2、T3、T4、T5、T6开始协调运动,回到其初始角度,最后右侧分支的末端夹持器夹紧,此时机器人完成了尺蠖运动的一个循环。
杆长为l,在一个运动循环中,移动距离为式(4):

可据此式求三分支机器人采用尺蠖步态在不同移动距离时的各关节转角。
3.2 翻滚步态
翻滚步态有两种,第一种为移动速度最快的翻滚步态,但相对于尺蠖步态会占用更大的空间,可以在高度不超过8L的空间内移动,如图3所示。

图3 三分支机器人的翻滚步态一Fig.3 The tumbling gait 1 of the climbing robots with three branches
其攀爬步骤如下:
1)机器人处于初始位置,左右两个分支的夹持器均处于夹紧状态,左侧分支的末端夹持器慢慢张开,右侧分支的末端夹持器保持夹紧,支撑机器人,如图3(a)所示。
2)左侧分支的末端夹持器松开,右侧分支的末端夹持器保持夹紧状态,T1关节顺时针转动90°-α(α按照图 3中方式定义),T2、T3关节顺时针转动,T逆时针转动, T、T、T向相4456反的方向转过相同的角度,如图3(b)所示。
3)摆动关节 T1、T2、T3、T4、T5、T6开始协调运动,回到其初始角度,第三个分支末端的夹持器夹紧,此时机器人完成了翻滚运动的一个循环。其中T1关节顺时针转动90°-α,T2、T3关节顺时针转动,T逆时针转动, T、T、T向相反的4456方向转过相同的角度,如图3(c)所示。
这种攀爬步态中,摆动角度最大的摆动关节为T6关节,摆动角度为θ=180°-2α。这一个运动周期的攀爬移动距离为式(5):
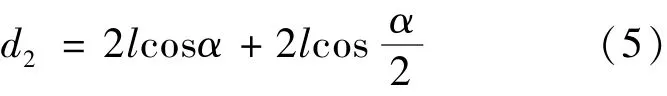
可据此式求三分支机器人采用翻滚步态一在不同移动距离时的关节转角。
第二种步态为针对地面实验规划的翻滚步态,占用空间最大,可以在高度不超过10l的空间内运动,如图4所示。

图4 三分支攀爬机器人的翻滚步态二Fig.4 The tumbling gait 2 of the climbing robots with three branches
其攀爬步骤如下:
1)机器人处于初始位置,左右两个夹持器均处于夹紧状态,左端第一个夹持器张开,右端及中间夹持器保持夹紧状态,支承机器人。
2)左侧分支的末端夹持器松开,右端及中间夹持器保持夹紧状态,摆动关节 Ti(i=1、2、3、4、5、6)开始协调运动,其中T1关节顺时针转动2(90°- α ),T2、T3关节顺时针转动 α,T4逆时针转动α,T4顺时针转过90°+, T6、T8、T9、T10逆时针转动一定角度。
3)左侧分支的末端夹持器松开,右端及中间夹持器保持夹紧状态,各摆动关节开始协调运动,回到其初始角度,第三个分支末端的夹持器夹紧,此时机器人完成了尺蠖运动的一个循环。
在翻滚步态二中,摆动角度最大的关节为T10,如图4所示,图中每个关节长度均为l。T9关节处角度为β=arcsin(1.5-sinα-sin),故在一个步态循环中最大运动角度为T10的摆动角度为270°-2α+β。在一个步态循环周期中移动距离为式(6):

可据此式求出三分支机器人采用翻滚步态二在不同移动距离时的关节转角。
4 攀爬过程步态分析
为对三个不同的步态进行对比分析,进行如下假设:关节的运动为三段式匀角加速运动方式,角加速度为a,最大角速度为ωmax,且均以最大角加速度加速到ωmax。即关节的运动轨迹为梯形角速度曲线。如图5(a)所示,在尺蠖步态时,关节T1首先匀加速到角速度为ωmax,保持一段时间后匀减速到 -ωmax,保持一段时间后速度恢复到0;T1关节摆动角度θ1首先由90°增大到90°+α,之后再恢复为90°。如图5(b)所示,在翻滚步态一中,关节T6首先匀加速到角速度为ωmax,保持一段时间后匀减速到0;摆动关节T6摆动角度由90°+α 增加到 270°⁃α。 如图 5(c)所示,在翻滚步态二时,关节T10首先匀加速到角速度为ωmax,保持一段时间后匀减速到 -ωmax,保持一段时间后速度恢复到0;T10关节摆动角度θ10首先由90°⁃arcsin(1.5⁃sinα⁃sin)增大到 270°⁃α,之后再恢复为90°+α。

图5 三种运动步态的梯形运动轨迹Fig.5 Trapezoidal trajectory of three kinds of gaits
分析一个分支可以独立运动的尺蠖步态在一个运动周期中的移动距离、摆动关节最大摆角、在梯形运动轨迹下的匀角加减速运动中的运动时间及运动速度,可知在梯形运动轨迹下的匀角加减速运动中,移动速度较慢,一个运动周期内的移动距离较小,在α较小时关节摆动角度较大。一个运动周期内的运动情况如式(7)~(8)所示:
关节最大摆角:

移动时间:

相对于二分支攀爬机器人[9⁃10],由于三分支机器人的尺蠖步态中存在一个独立的运动分支,可以在移动过程中执行较为复杂的空间站任务。
第二种是通过模拟猿猴攀爬时的运动方式提出的翻滚步态一。在梯形运动轨迹下的匀角加减速运动中,一个运动周期内的移动距离较远,速度较快,但是相对于尺蠖步态来说,全部的分支都用于攀爬运动,没有独立的运动分支。一个运动周期内的运动情况如式(9)~(10)所示:
关节最大摆角:

移动时间:

在图6可以看出与二分支机器人的移动步态[9⁃10]相比,三分支机器人关节的摆动角度可以减小2α,在关节最大转动角速度相同的情况下,在一个运动周期中可以减少的时间,大大提高攀爬机器人的移动速度,对攀爬机器人在空间站内执行复杂的操作任务有巨大的帮助。减小关节的最大摆动角度同时可以攀爬机器人的关节设计难度。
图6 二分支尺蠖运动步态Fig.6 Tumbling gait of the climbing robots with two branche
第三种步态是针对地面试验提出的翻滚步态二,相对于翻滚步态一,在运动周期的任意时刻都可以保证至少有两个夹持器处于夹持状态,可以提高地面试验的可行性及安全性。相对于尺蠖步态,在梯形运动轨迹下的匀角加减速运动中,一个运动周期内的移动距离较远,速度较快;相对于翻滚步态一,一个运动周期内的移动距离相同,但运动的周期更长,速度较慢,关节摆动角度也相对较大,是一种针对于地面试验的运动方式。一个运动周期内的运动情况如式(11)~(12)所示:
关节最大摆角:

移动时间为:

5 结论
本文针对9自由度的三分支攀爬机器人提出了三种运动步态:可以采用具有独立运动机械臂并在移动中执行复杂空间站任务的尺蠖步态,关节最大摆动角度较小、移动速度较快的翻滚步态一,以及针对地面试验在运动周期的任意时刻至少有两个夹持器处于夹持状态的翻滚步态二。通过梯形角速度运动轨迹对三种步态在一个运动周期内的运动进行分析发现,这三种步态解决了二分支攀爬机器人及单臂机器人在移动速度较慢、关节转角过大、无在移动中可执行复杂操作任务的独立分支这三个方面的不足。
(
)
[1] Nechyba M C,Xu Y S.Human robot cooperation in space:SM2 for new space station structure[J].IEEE Robotics&Automation Magazine,1995,2(4):4⁃11.
[2] Xu Y,Brown B,Friedman M,et al.Control system of self⁃mobile space manipulator[ C] //Robotics and Automation,1992.Proceedings,1992 IEEE International Conference on.IEEE, 1992: 866⁃871.
[3] 孙汉旭,王凤翔.加拿大,美国空间机器人研究情况[J].航天技术与民品, 1999(4): 33⁃35.Sun Hanxu,Wang Fengxiang.Research on space robots in Canada and the United States[J].Aerospace Technology and Civilian Products, 1999(4): 33⁃35.(in Chinese)
[4] 刘宏,蒋再男,刘业超.空间机械臂技术发展综述[J].载人航天, 2015, 21 (5):435⁃443.Liu Hong, Chiang Chiang, Liu Yechao.Review of space ma⁃nipulator technology[ J].Manned Spaceflight, 2015, 21(5):435⁃443.(in Chinese)
[5] Almonacid M,Saltaren R,Aracil R,et al.Motion planning of a climbing parallel robot[J].IEEE Transactions on Robot⁃ics and Automation, 2003, 19(3): 485⁃489.
[6] 曹志华,陆小龙,赵世平,等.电力铁塔攀爬机器人的步态分析[J]. 西安交通大学学报, 2011, 45(8):67⁃72.Cao Zhihua, Lu Xiaolong, Zhao Shiping, et al.Gait analysis for electricity pylon climbing robot[J].Journal of Xi’an Jiao⁃tong University, 2011, 45(8):67⁃72.(in Chinese)
[7] Balaguer C,Gimenez A,Jardon A.Climbing robot mobility for inspection and maintenance of 3D complex environments[J].Autonomous Robots, 2005, 18(2): 157⁃159.
[ 8 ] Shvalb N, Moshe B B, Medina O.A real⁃time motion plan⁃ning algorithm for a hyper⁃redundant set of mechanisms[J].Robotica, 2013, 31(8): 1327⁃1335.
[9] 江励,管贻生,蔡传武,等.仿生攀爬机器人的步态分析[J]. 机械工程学报,2010,46(15):17⁃22.Jiang Li, Guan Yisheng, Cai Chuanwu, et al.The gait analy⁃sis of the bionic climbing robot[J].Journal of Mechanical Engineering, 2010, 46 (15): 17⁃22.(in Chinese)
[10] GUAN Yisheng,JIANG Li,ZHANG Xianmin,et al.Develop⁃ment of novel robotic systems with modular methodology[C]//IEEE/RSJ International Conference on Intelligent Ro⁃bots and Systems,October 10⁃15,2009,St.Louis,USA.New York:IEEE,2009:2 385⁃2 390.

