空管自动化系统嵌套CA告警区绘制的几何规律浅析
郑康晓
(中国民用航空珠海进近管制中心技术保障部,广东珠海,519015)
1 CA告警区绘制类型
当前国内主流空管自动化系统多种多样,如aerotrac自动化系统、欧洲猫自动化系统、ATC3000自动化系统、莱斯自动化系统等,但告警区的绘制都大同小异,整体分为矩形和多边形两种绘制类型。两种绘制类型不可混杂,即矩形告警区中无法包含多边形方法绘制的告警区,反之亦然。CA告警区绘制时均为平面图,告警区的高度范围在参数中设置。
矩形告警区的绘制,需要技术人员给出左上角和右下角两个顶点经纬度,或者给出北纬、南纬、东经、西经四个参数。如图1所示。

图1 矩形告警区绘制
多边形告警区的绘制,需要技术人员按顺序给出边界顶点,按照顺序连接顶点,形成闭合的告警区。图2给出了多边形告警区的绘制图示。
2 嵌套CA告警区的计算规则
CA告警的主要告警参数有最小接近距离和最小高度差。当航空器同时满足水平距离小于最小接近距离,以及高度差小于最小高度差这两个条件时产生CA告警。如图3所示,假如矩形告警区B嵌套在矩形告警区A中,且二者的最小接近距离和最小高度差设置均不相同。那么B告警区的CA告警计算遵循下列规则:

图2 多边形告警区绘制
(1)A区告警参数大于B区告警参数时,按照A区告警参数计算B区告警。
(2)A区告警参数小于B区告警参数时,按照B区告警参数计算B区告警。
(3)A区告警参数部分大于B区告警参数时,按照较大的参数计算B区告警。
总而言之,当CA告警区存在重叠区域时,重叠区域中的CA告警总是按照较为严格的参数标准来计算。由此可见,在第一种和第三种情况时,图3这样的告警区绘制方式无法达到原本的告警区划分效果。本文接下来将分别就矩形CA告警区和多边形CA告警区讨论这两种情况下的绘制方案。
3 矩形CA告警区的嵌套
3.1 单个独立告警区嵌套
如图3所示,A和B告警区边界和边界延长线均没有重合,我们称之为独立告警区嵌套。这种情况下,我们要达到无论何种情况,A区和B区都分别采用各自告警参数计算的目的,图4给出了一种解决方案的两种绘制方法:将原告警区A划分为A1、A2、A3、A4四个与原A区参数一样的告警区,B区依旧保留,这样一共5个告警区,不存在重叠区域。这种方案虽然不是唯一,但却是告警区数目最少的一种绘制方案。

图3 矩形告警区嵌套
3.2 多个独立告警区嵌套
上述情况是一个独立告警区的嵌套,接下来讨论嵌套多个独立告警区的情况。图5给出了两个独立告警区B和C嵌套在A告警区中的绘制方案,我们可以理解为在图4(左)的基础上,将告警区C嵌套在图4(左)的A3区中,即将原本的A3区划分为A3、A5、A6、A7和C5个告警区,一共9个告警区。按照这个规律,我们可以推算出,如果有N个独立矩形告警区嵌套在一个矩形告警区内部,那么该告警区最少需要划分为4N+1个矩形告警区,才能实现划分目的。

图4 单个独立矩形告警区嵌套的绘制方案
3.3 非独立告警区嵌套
当告警区有边界或边界延长线重合时,我们称之为非独立告警区。非独立告警区嵌套的情况比较复杂,图6给出了常见各种情况下的绘制方案,6-a是嵌套告警区B和原告警区A边界重合的情况,6-b是两个嵌套告警区B和C边界延长线重合的情况,6-c是嵌套告警区B和C公用顶点的情况,6-d是嵌套告警区B和C边界重合的情况,等等诸如此类,不胜枚举。那么是否没有规律呢?答案是否定的,接下来笔者将逐步分析其中的规律。
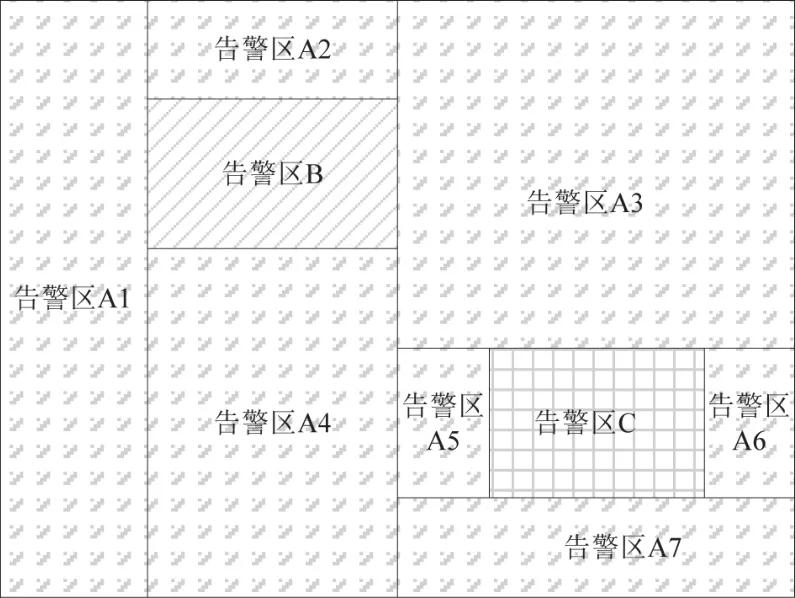
图5 两个独立矩形告警区嵌套的绘制方案
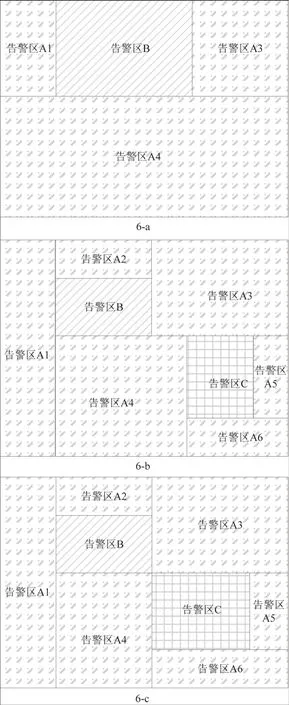

图6 非独立告警区嵌套的各种情况
我们从告警区划分方案的生成来考虑,图7-a是最基本的单告警区嵌套。我们可以看到,告警区B四条边的延长线,即两横两竖四条线将告警区划分为9个区域。而每个顶点处的四个区域,可以将其中两个相邻区域合并,从而压缩一个区域。因此,我们大胆假设:如果嵌套告警区有M条横线,N条竖线,D个顶点,那么最少需要划分的区域个数为(M+1)×(N+1)-D.单个矩形的情况下,M=N=2,D=4,计算结果为5个,符合实际情况。图7-b的情况下,M=1,N=2,D=2,计算结果为4个,同6-a相符合。
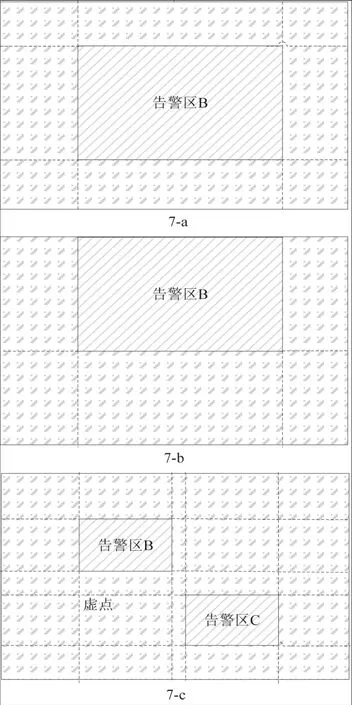
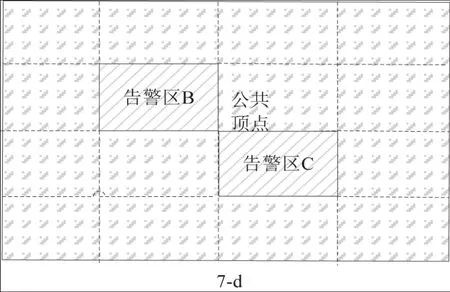
图7 矩形告警区嵌套规律分析
但是,在图5的情况下,M=4,N=4,D=8,公式计算结果为25-8=17,与实际的9个告警区数目不吻合。因此我们需要修正公式。图7-c展示了图5告警区的生成,图中虚线的交叉点我们称之为虚点,虚点和四条虚线围成的矩形数据比例为1:1,而虚线围成的矩形实际上都是可以与其他矩形合并的。所以每一个虚点的存在,同样会减少一个矩形告警区。虚点和告警区的顶点总数,就是横线和竖线的交叉点数目,一共M×N个。修正后的公式为(M+1)×(N+1)-M×N,简单的运算后,即 M+N+1。
图5的情况下,M=N=4,计算结果为9,与实际相符。考虑到图7-d的情况,告警区B和告警区C之间,有一个特殊的公共顶点。这个公共顶点处的四个区域无法被合并,因此如果类似图中这样的公共顶点数目为G,最少需要划分的告警区数量为:M+N+G+1。

表1 矩形CA告警区嵌套最小划分数量公式验证结果
下面我们对这个公式进行进一步的验证,从表1可以看出,这个公式符合所有矩形告警区的嵌套结果,包括独立、非独立、单个以及多个的情况。最后我们得出结论:矩形CA告警区的嵌套,嵌套告警区边界延长线中,横线数目为M,竖线数目为N,且嵌套告警区之间,不在公共边上的公共顶点数目为G,那么最少需要划分的矩形告警区数量n的计算公式如:n=M+N+G+1。
4 多边形CA告警区的嵌套
从第一部分的介绍我们知道,多边形告警区的绘制是按顺序连接顶点成为一个封闭的多边形。图7左图是最简单的一种嵌套,独立告警区B嵌套在告警区A当中。那么我们的绘制方案如图7右图:将告警区A划分为A1和A2两个参数相同的告警区。A1的顶点绘制顺序为1,4,3,8,7,5;A2的顶点绘制顺序为1,2,3,8,6,5.一共绘制三个告警区即可。
多个独立告警区的绘制方法与之相同,如图8所示,将每一个多边形的两个顶点分别与其它多边形相连,原告警区A始终只需要被拆分为两个告警区,如果嵌套的独立告警区数目为N,那么最终划分的告警区数目恒定为2+N。

图8 单个独立多边形告警区嵌套
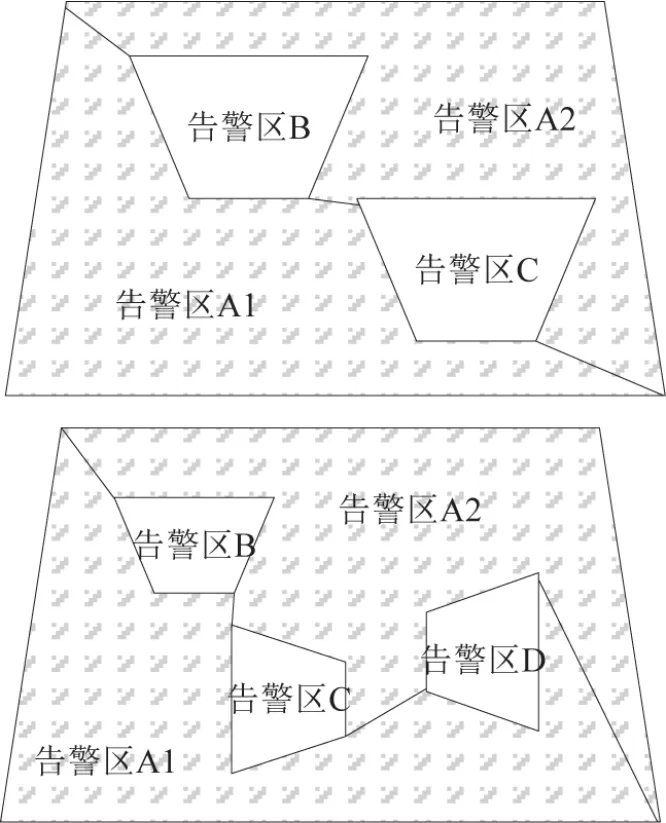
图9 多个独立多边形告警区嵌套

图10 非独立多边形告警区嵌套
最后考虑非独立多边形告警区嵌套的情况。从图9可看出,在这种绘制方式下,无论告警区之间是否存在公共边、公共顶点,都不会影响最终划分的告警区数目,依然恒定为2+N个,其中N为嵌套告警区的数量。
5 结束语
CA告警区作为空管自动化系统的重要参数,其划分和配置方法是维护人员必须掌握的基础技术。本文介绍了笔者在绘制CA告警区过程中总结出的一些几何规律,从中可以看出,矩形告警区形状规则,但如果存在嵌套时需要划分的告警区数量繁多,工作量大。而多边形告警区在存在嵌套时划分方法简单,工作量小。因此在配置CA告警时需要结合实际情况,选择适合的告警区绘制方法。笔者经验所限,难免有疏漏之处,欢迎广大同行批评指正。
[1]谢华.空管自动化系统的一个故障案例分析[J].电脑知识与技术:学术交流.2014(30):7177-7179.
[2]周辉.空管自动化系统大面积DUPE告警故障分析[J].数字通信世界.2017(10).

