奇数网格(或棋盘)德杰尼斯问题解法
李 盘 林, 赵 铭 伟, 徐 喜 荣, 李 丽 双, 李 伯 章
( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024; 2.滑铁卢大学 计算机工程系, 加拿大 安大略 滑铁卢 )
0 引 言
鉴于五后问题的由来,作者在文献[1]中将它称为德杰尼斯五后问题,并先后进行了德杰尼斯五后问题解法[2]和德杰尼斯五后问题泛化研究[3].文献[3]是将文献[2]的论域8×8网格(或棋盘)推广到2p×2p网格(或棋盘)(p=1,2,…)上.
若对任意偶数e,称e×e网格(或棋盘)为偶数网格(或棋盘),用数学语言可表为2p×2p网格(或棋盘)(p=1,2,…);若对任意奇数o,称o×o网格(或棋盘)为奇数网格(或棋盘),用数学语言可表为(2p+1)×(2p+1)网格(或棋盘)(p=1,2,…,p=0为平凡情形).于是,文献[3]题目又可表述为偶数网格(或棋盘)德杰尼斯问题解法.虽然只有一字之差,但是两者解决问题的方法还是有所区别的.将本文与文献[3]合并起来,便得到一个新论题:对任意自然数n,n×n网格(或棋盘)德杰尼斯问题解法.可见,本文和文献[3]对这一论题的完成是不可或缺的.
1 求解前的准备
奇数网格(或棋盘)坐标表示如图1所示.
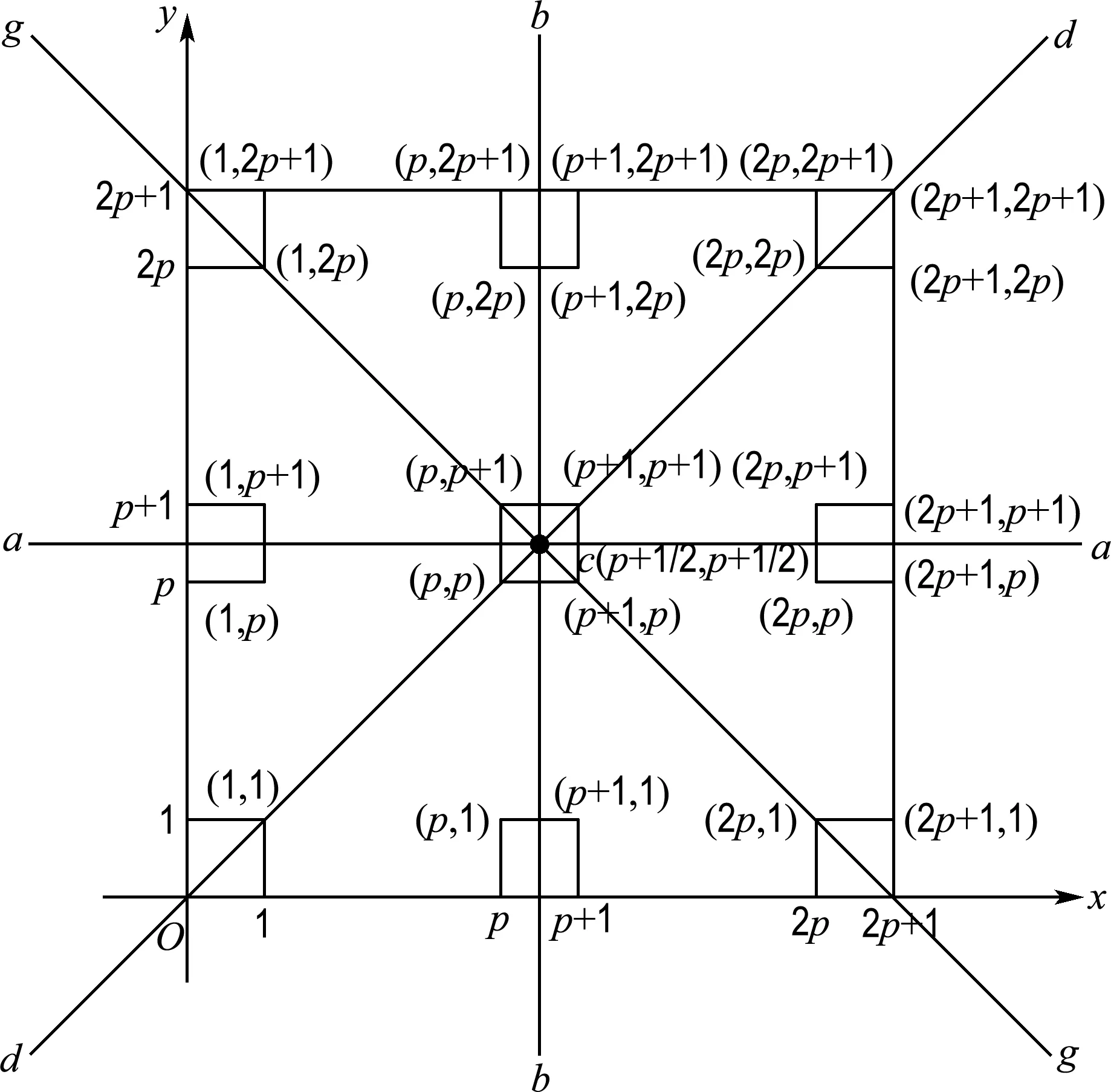
图1 (2p+1)×(2p+1)网格坐标图示Fig.1 Coordinate illustration of (2p+1)×(2p+1) grid
从图1可知,该图形是关于直线aa、bb、dd和gg对称的,它们相交于c,其坐标为(p+1/2,p+1/2),以c为中心的格,称为中心格,表示为sp+1,p+1.可见,本文格仍沿用文献[2]或文献[3]的表示方式,即用格的右上角顶坐标来表示.为方便计,si,j简记为sij.
定义1S={sij|1≤i,j≤2p+1},即用S表示(2p+1)×(2p+1)网格中的所有格集合.(文献[2]中是用C表示的)
定义2位于直线dd和bb上及其它们相交域(夹角≤90°)内的所有格,称为解首格集,表示为
Sf={sij|j≤i≤p+1,1≤j≤p+1}
与文献[1]、[2]中相同的定义,在此不再赘述.
又令Sfr={sij|sp-r+2p-r+2,sp-r+3p-r+2,…,sp+1p-r+2}为Sf中从中心点c向下第r列中格的集合,则有下面定理:
定理1Sf=Sf1∪Sf2∪…∪Sfp+1,且Sij=r,1≤r≤p+1.
定理2对任意sij∈Sf,j≤i≤p+1,1≤j≤p+1,则
6p+2j-1≤n(sij)≤8p+1
定理1和定理2的验证留给读者完成.
2 解 法
首先选取si1j1∈Sf,使n(si1j1)为最大,作为第一个广义解的首格,由定理2知,si1j1≠sp+1p+1,即si1j1∈Sf1.接着选取si1j1的马步格,其集合表为H1.若H1∩(S-si1j1)≠,则将H1∩(S-si1j1)中格按剩余控制数排序,择取最大(或极大,这时不止一个格,下同)者作为第一个广义解的第2格si2j2;若H1∩(S-si1j1)=,则将(S-si1j1)中格按剩余控制数排序,择其最大(或极大)者作为第一个广义解的第2格si2j2.继而,选取{si1j1,si2j2}的马步格,其集合表为H2.若H2∩(S-si1j1-si2j2)≠,则将H2∩(S-si1j1-si2j2)中格按剩余控制数排序,择取最大(或极大)者作为第一个广义解的第3格si3j3;若H2∩(S-si1j1-si2j2)=,则将(S-si1j1-si2j2)中格按剩余控制数排序,择其最大(或极大)者作为第一个广义解的第3格si3j3.依此类推,求出第一个广义解的第4格si4j4,…,第k-1格sik-1jk-1.于是选取{si1j1,si2j2,…,sik-1jk-1}的马步格,其集合表为Hk-1.若Hk-1∩(S-si1j1-si2j2-…-sik-1jk-1)≠,将Hk-1∩(S-si1j1-si2j2-…-sik-1jk-1)中格按剩余控制数排序,择取最大(或极大)者作为第一个广义解的第k格sikjk;若Hk-1∩(S-si1j1-si2j2-…-sik-1jk-1)=,则将(S-si1j1-si2j2-…-sik-1jk-1)中格按剩余控制数排序,择其最大(或极大)者作为第一个广义解的第k格sikjk.
需要指出的是:
(1)在求广义解的第h格sihjh(h≥2)时,若n(sihjh) 为极大时,则有多个格,其剩余控制数与n(sihjh) 相同,不妨令n(sx1y1)=n(sx2y2)=…=n(siuju),其中sx1y1=s′x1y1,以及sxvyv(2≤v≤u)为第一个广义解的第h格.选出{si1j1,si2j2,…,sin-1jn-1,sxvyv}(2≤v≤u)的马步格,其集合表为Hv.若(Hv-{sx1y1}-…-{sxv-1yv-1})∩(S-si1j1-…-sin-1jn-1-sxvyv)中格按剩余控制数排序,择其最大(或极大)者作为第一个广义解的第h+1格sih+1jh+1;否则将(S-si1j1-…-sin-1jn-1-sxvyv)中格按剩余控制数排序,择其最大(或极大)者作为第一个广义解的第h+1格sih+1jh+1.如此这般,便可依次求出以sx2y2,sx3y3,…,sxuyu为第h格的广义解.
(2)要求出以Sf中的每一个格为首格的基础解,即按Sf中子集次序Sf1,Sf2,…,Sfp+1求出它们中每一格为首格的基础解.
定义3若
则称{siljl|1≤l≤k}为所求的第一个广义解,其广义解中格的个数,称为该广义解的基数或长度.
类似求第一个广义解那样,求第二个广义解.第二个广义解的首格,可以是si1j1即sp+1p+1,但也可能不是sp+1p+1,而是Sfr中的其他格(r≥2).这与p的取值有关.取上述二广义解的基数或长度小者,称为问题候选基础解;若上述二广义解的基数或长度相同,则它们便都是问题候选基础解.而候选基础解中格的个数,称为候选基础解的基数或长度.
在求解过程中,若当前广义解,其基数或长度比以前候选基础解的基数或长度小,则取当前广义解为该问题的候选基础解.仿上,求出后面的候选基础解.由此可知,在整个求解过程中,存在候选基础解的基数或长度不再是变小的一些解,称这些(或这个)解为问题的基础解.基础解中格的个数,称为基础解的基数或长度.
根据奇数网格(或棋盘)图形对称性,可得下面定理:
定理3对任给定奇数o(o≥5),若求出o×o网格(或棋盘)德杰尼斯问题的no个不同基础解,则它将有4×no个不同解.
为便于理解问题的解法,下面给出了图2~4,分别是3×3网格、5×5网格和7×7网格德杰尼斯问题的1个、3个和24个基础解.

3 结 语
本文完成了奇数网格(或棋盘)德杰尼斯问题解法,它与文献[2]共同给出了对任意自然数n,n×n网格(或棋盘)德杰尼斯问题求解.这不仅具有一定的理论价值,而且在防灾减灾和安全领域中前景利好.
[1] 李盘林,李丽双,赵铭伟,等. 离散数学[M]. 3版. 北京:高等教育出版社, 2016.
LI Panlin, LI Lishuang, ZHAO Mingwei,etal.DiscreteMathematics[M]. 3rd ed. Beijing: Higher Education Press, 2016. (in Chinese)
[2]李盘林,赵铭伟,徐喜荣,等. 德杰尼斯五后问题求解方法[J], 大连理工大学学报, 2016,56(3):304-308.
LI Panlin, ZHAO Mingwei, XU Xirong,etal. Solution to De Jaenisch′s five queens problem [J].JournalofDalianUniversityofTechnology, 2016,56(3):304-308. (in Chinese)
[3]李盘林,赵铭伟,徐喜荣,等. 德杰尼斯五后问题泛化研究[J]. 大连理工大学学报, 2017,57(3):327-330.
LI Panlin, ZHAO Mingwei, XU Xirong,etal. Research on generalization of De Jaenisch′s five queens problem [J].JournalofDalianUniversityofTechnology, 2017,57(3):327-330. (in Chinese)

