改进遗传算法求解面向订单多目标排产问题

武韶敏，胡晓兵，王江武，徐兴伟

（四川大学 制造科学与工程学院，四川 成都 610065）

1 引言

随着市场经济的深度发展和生产技术的逐步成熟，我国中小型制造企业也得到了极大的发展，面对竞争日趋激烈的市场和客户需求的个性化，订单式生产（Make To Order，MTO）也成为我国绝大多数中小型企业广泛采用的一种生产模式[1]。生产调度是现代制造系统的一个重要问题，在企业的生产管理和市场竞争力中扮演着十分重要的角色。作业车间调度问题（Job Shop Scheduling Problem，JSSP）方面，文献[2]采用启发式倒排算法来求解加工调度问题，文献[3]提出一种基于自适应遗传算法的多目标柔性作业车间动态调度算法，文献[4]针对JSSP问题提出一种基于知识的蚁群算法，但以上研究工作都是针对作业车间的局部排产，没有从全局多作业车间或多生产单元的高度对订单进行排产规划。面向订单生产方面，文献[5]提出一种考虑备货时间灵活性的订单选择和排产模型，文献[6]研究了基于客户满意度的订单排产策略，文献[7]研究了单任务的多个订单的接受和排产问题，并给出基于遗传算法的求解模型，文献[8]研究了从有限生产能力和产出缓存方面考虑订单选择策略，但以上研究大都将单个订单看成整体进行排产，而实际生产过程中，特别是对于制造企业，每个订单都由多个生产任务组成。文献[9]研究了多任务组成订单的排产，但是基于车间环境的。基于以上研究分析，提出一种更加符合面向订单生产型企业生产实际的订单排产思路，从全局的高度出发，将多个订单拆解后的任务安排在多个生产单元协调生产，综合考虑订单的准时交付、企业生产成本和生产平衡多个指标对订单排产优化。

2 问题描述

所研究的是在一个确定的排产周期T内对订单进行排产，首先将原始订单进行拆解，确保拆解后订单的生产任务只包含一种产品，订单的工艺过程、交货日期等属性完全一致；将拆解后的订单安排在N个生产单元上，每个生产单元完成产品的部分加工过程，且产品在生产单元的加工工序有先后约束，每个生产单元有最大负荷约束；在满足工序约束和最大负荷约束的情况下，通过优化排产来最小化排产周期内订单的延期时间、库存时间和平衡各生产单元的机器负荷，是一个多目标优化的NP-hard问题。

2.1 问题假设及符号

假设1，订单在每一个生产单元的生产任务都可以在一个工作日内完成。假设2，订单在各生产单元的加工时间已知，且在完成在前一个生产单元上的生产任务后才能在下一个生产单元上加工。订单排产数学模型所使用的符号定义，如表1所示。

表1 符号定义Tab.1 Symbol Definition

2.2 模型建立

订单的排产周期为T，t为计划周期的基本单位，在本模型中t代表工作日，每个工作日生产单元i的可用最大载荷为Cmaxit。排产周期内涉及的订单集合为 O=｛O1，O2，…，Oi，…，On｝，n 为正整数。订单 k 中产品的工艺流程集合为 Jk=｛Jk1，Jk2，…Jkm｝1≤k≤n，需要说明的是，在本模型中工艺流程是与生产单元一一对应的，即将在工艺流程数量等于订单从开始加工到完成生产所经过的生产单元的总和。决策变量：

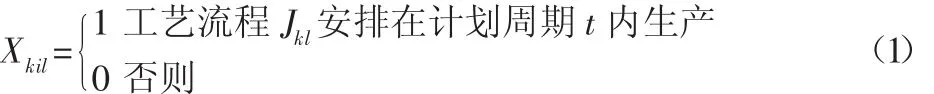
目标函数，结合生产实际，为了能够最大限度的优化订单排产效果，从订单的延期成本、库存成本和工作单元负荷的平衡三方面指标来衡量排产的优劣。

（1）延期成本：每个订单都指定的交货日期，超过订单交货日期势必会给企业带来一定的损失，且损失与订单的权重和延期时间长短有关。此外，延期订单的数量也是一个非常重要的指标。因此，延期成本的计算分为延期订单的数量和延期时间两部分：

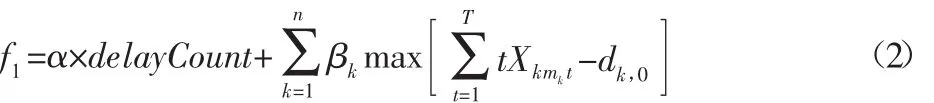
式中：mk—订单k的最后一道工艺流程；delayCount—延期订单数量。

（2）库存成本：订单的库存是指在订单完成后和交货日期前停留在仓库的时间间隔。订单的库存成本如式（3）所示：

式中：库存时间惩罚系数γk是与各订单中产品数量正相关的。

（3）工作单元的载荷均衡：订单排产中保证工作单元的负荷均衡，有利于降低机器的损坏，延长使用寿命。载荷均衡见式：

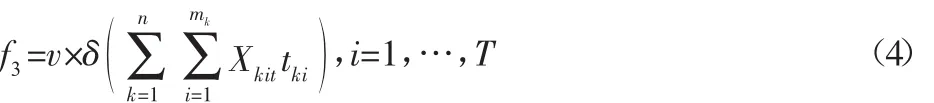
的标准差；v—负载均衡的惩罚系数。

通过给订单延期成本、库存成本和载荷均衡三个指标赋予不同的权重系数ω1、ω2、ω3形成一个目标函数，如式（5）所示。每个订单的所有工艺流程都必须分配在某个计划周期单元t内生产，如式（6）所示。订单的工艺约束，即单个订单的工艺流程必须在上一工艺流程结束后才能开始生产，如式（7）所示。生产单元的生产能力约束，即对任意工作日t，安排在生产单元上的任务不能超过生产单元的最大负荷，如式（8）所示。

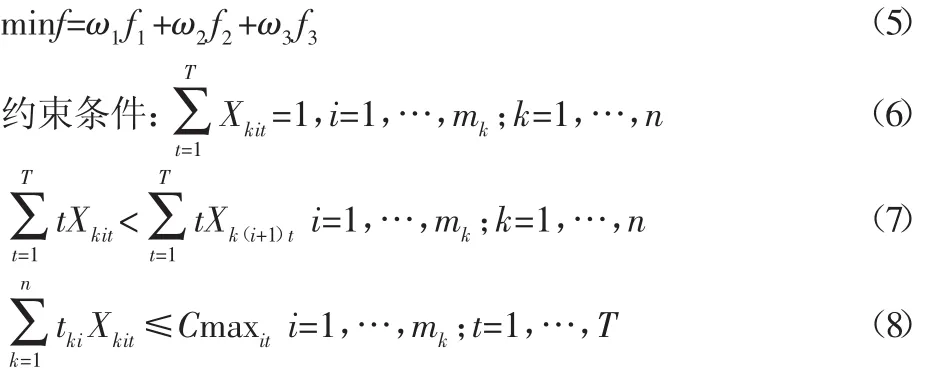
3 算法求解

结合实际数学模型，采用改进遗传算法进行求解，优化排产。

3.1 矩阵实数编码

采用一个N×J的矩阵来表示遗传算法中的一个个体，即一种订单排产的解决方案，矩阵采用实数编码如下所示：

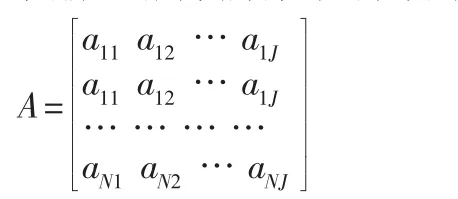
矩阵A的每一行代表一个订单任务，共有N个订单任务；矩阵每列对应的一个加工单元，也就是一个工艺流程。矩阵中元素aii的行标i表示第i个订单，列标j表示第j个工艺流程，aii的取值是［0，T］的整数，表示订单i的第j个工艺流程在第aii个计划周期单元进行加工。

3.2 初始种群的产生

初始种群的个体是按行产生的。为了满足工艺约束式（9），每个订单从最后一道工艺流程开始随机产生加工时间aiJ∈［1，T］，接着为倒数第二道工艺流程随机分配加工时间aiJ-1∈［1，aiJ］，以此类推完成单个订单的所有工艺流程的排产，进而完成所有订单的排产。这种方法产生的初始种群个体必然满足订单任务的工艺约束（7），但并不一定满足生产能力约束（8），因此对产生的个体还要进行校验，是否超过生产单元的最大负荷，如果超过则是不可行解，要按以上步骤重新产生个体，直到满足生产能力约束（8）。

3.3 交叉算子

算法采用实数矩阵编码，传统常用的单点交叉、多点交叉、均匀交叉等适用性有限，为了能使种群个体间交叉更加有效，设计了行交叉和列交叉两种交叉算子。

3.3.1 行交叉算子

针对N×J阶矩阵编码的个体A，随机产生一个由0和1组成的N维向量。对于父辈中任意的两个体An和An+1，若N（i）=1，则对An和An+1的第i行进行交换，若N（i）=0则不进行任何操作。以此类推，种群中的任何两个体都根据随机为其产生的N维向量完成行交叉。根据以上的行交叉算子产生的子代CAn和CAn+1都必然满足订单产品工艺约束（7），但并不一定满足生产能力约束（8），因此每次交叉完成后都要对产生的两个新个体进行校验，若不满足，则要采用如图1修复策略。对于满足载荷约束的，则采用局部锦标赛法，比较父辈个体和子代个体的适应值，保留适应值较大的个体。

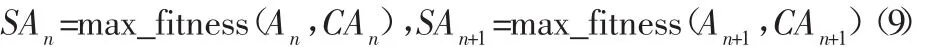
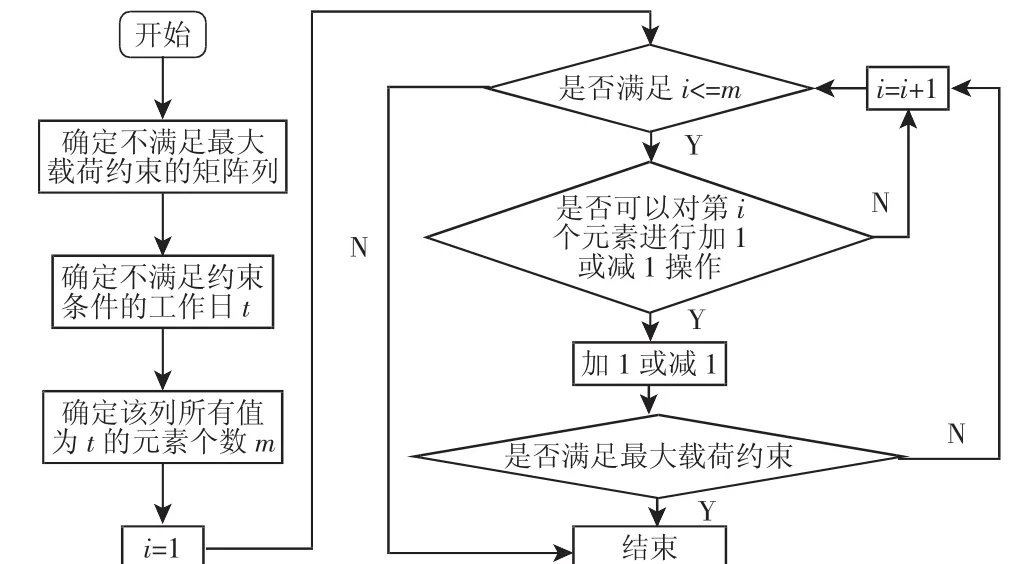
图1 行交叉算子修复策略流程图Fig.1 Flow Chart of Row-Based Crossover Operator Repair Strategy

3.3.2 列交叉算子

列交叉算子的设计和行交叉算子的设计思路类似，对于种群的每两个父代个体都随机产生一个由0和1组成的维向量作为交叉模板。但不同的是，两父辈个体列交叉后产生的两子代个体通常都不满足订单产品的工艺顺序约束式子（7），因此需要对其进行修复。首先对新产生矩阵个体的每行从小到大重排使其满足工艺约束，然后对个体进行工作单元最大载荷约束检验，若不满足则舍弃该个体。对于满足条件的，同样采用局部锦标赛法保留父辈和子代中适应值较高的个体。

3.4 变异算子

变异算子的设计也有行变异算子和列变异算子两种。两种变异算子同样采用由0和1组成的向量作为变异模板，数值的变异规则如下：

式中：di—第i个订单的发货日期；T—整个排产计划周期。

变异规则（10）的说明：当个体矩阵的第i行最大值小于等于di，即该订单不会延期时，该行所有元素采用di-aij+1的变异规则，确保了变异后产生的数值同样在［1，di］范围内，即仍是不延期订单，这样保证在有效变异的同时也保留个体的优良特征。当个体矩阵的第i行最大值大于di，即该订单为延期订单，该行所有元素采用T-aij+1的变异规则。

3.5 适应值函数和选择算子

根据算法模型的目标函数式子（5），设计适应值函数如下：

选择算子则是根据个体的适应值采用轮盘赌的方法产生子代个体，假设种群规模为，则个体被选择的概率为：

4 实验仿真

4.1 参数设置

由于所提出模型不存在标准算例，为了保证数据的合理性。所采用实验数据是结合某机床厂的真实生产数据产生的，所有订单的生产任务在相应生产单元的生产时间是的随机数，单位为分钟，每个生产单元的单个工作日的最大载荷为1920min。程序运行环境为内存2G、主频2.67GHz的Win7操作系统的Matlab 2012平台。算法的参数设置如下：行交叉概率，列交叉概率，行变异概率，列变异概率，权重系数，延期订单数量的惩罚系数为，所有订单的延期时间惩罚系数均为，生产单元载荷均衡系数。

4.2 算法对比

现有文献中文献[10]的问题模型与建立模型最接近，都是多任务订单排产问题，且同样是针对最大载荷已知的多个生产单元进行排产，不同的是其排产过程中考虑到库存的影响。因此，下面同时采用文献[10]中的改进粒子群算法和提出的改进遗传算法解决提出的订单排产问题模型，并对解的结果进行对比分析。遗传算法的种群规模取100，进化代数取200，其他参数设置取4.1中的值。不同问题规模下两种算法的求解结果和求解时间比较，每组数据计算10次，是10次运算的所有结果中目标函数最小值，是10次运算目标函数最小值的平均值，是算法运行时间的平均值，单位为s，如表2所示。从表2可以看出，设计的改进遗传算法在优化结果和运算时间上都要优于参考文献中的改进粒子群算法。在（20×7）情况时，采用改进GA算法种群优化目标函数的平均值和最优值在整个进化过程中变化趋势，如图2所示。种群平均延期订单数、平均延期时间、平均库存时间及平均生产单元载荷标准差的变化情况，如图3和图4所示。从三图可以看出无论是总体目标还是各个指标的优化都非常显著。

表2 算法性能对比Tab.2 Algorithm Performance Comparison

图2 种群目标函数值Fig.2 Objective Function Value of the Populations

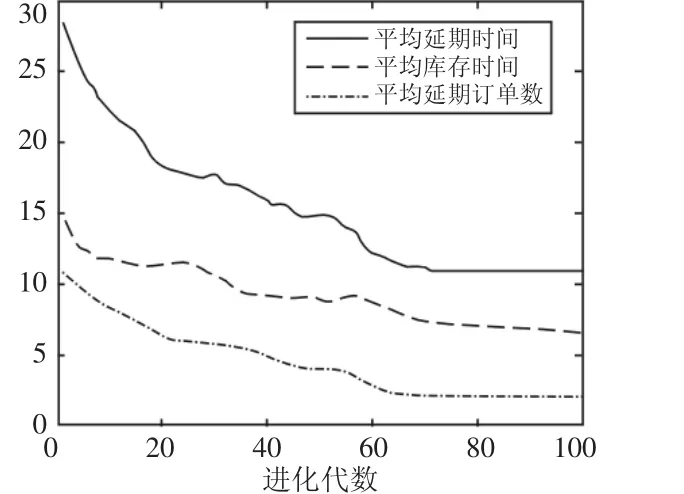
图3 延期订单数、延期时间及库存时间平均值Fig.3 Average Value of the Delayed Orders，Delay Time and Stock Time

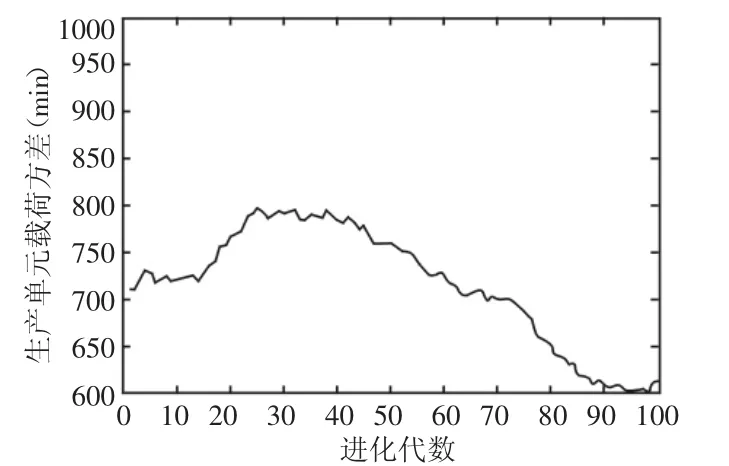
图4 生产单元载荷标准差Fig.4 Standard Deviation of Production Unit Load

5 结语

结合企业生产实际提出一种面向多目标排产优化的方法，综合考虑订单的延期成本、库存成本和生产单元的负载均衡三个优化指标，构建了排产优化的数学模型。设计了基于矩阵编码的改进遗传算法求解上述数学模型，通过对算法对比，验证了改进GA算法的有效性和优越性。

［1］邓毅.基于MTO的中小型制造企业订单排产优化研究［D］.广州：广东工业大学，2011.（DengYi.Orderproductionschedulingoptimizationresearchbasedonsmall and medium-sized manufacturing enterprise of MTO［R］.Guangzhou：Guangdong University of Technology，2011.）

［2］赵芳，姜莉莉，习小英.基于启发式倒排算法加工调度研究［J］.机械设计与制造，2010（12）：52-54（Zhao Fang，Jiang Li-li，Xi xiao-ying.Job shop scheduling problem of matching machine based on bacjward herisitic scheduling algorithm［J］.Machinery&Manufacture，2010（12）：52-54.）

［3］刘爱军，杨育，邢青松.柔性作业车间多目标动态调度［J］.计算机集成制造系统，2011，17（12）：2629-2637.（Liu Ai-jun，Yang Yu，Xing Qing-song.Dynamic scheduling on multiobjective flexible Job Shop［J］.Computer Integrated Manufacturing Systems，2011，17（12）：2629-2637.）

［4］Xing L N，Chen Y W，Wang P.A knowledge-based ant colony optimization for flexible job shop scheduling problems［J］.Applied Soft Computing，2010，10（3）：888-896.

［5］Ch K，G P M，K P.Order selection and scheduling with leadtime flexibility［J］.IIE Transactions，2004，36（7）：697-707.

［6］郭源生.基于顾客满意度的客户订单选择［J］.西安电子科技大学学报，2007，17（6）：36-40.（Guo Yuan-sheng.Options of customer orders based on customer satisfaction［J］.Journal of Xidian University，2007，17（6）：36-40.）

［7］Rom W O，Slotnick S A.Order acceptance using genetic algorithm［J］.Computers&Operations Research，2009，36（6）：1758-1767

［8］张欣，马士华.基于有限生产能力和产出缓存的订单接受策略［J］.工业工程与管理，2008（2）：35-40.（Zhang Xin，Ma Shi-hua.Order acceptance with limited capacity and finite output buffers in MTO environment［J］.Industrial Engineering and Management，2008（2）：35-40.）

［9］Siddharth M，Purushothaman D，CHEN C S.A branch and price solution approach for order acceptance and capacity planning in make-to-order operations［J］.European Journal of Operational Research，2011，211（3）：480-495.

［10］ZHANG T，ZHENG Q，FANG Y.Multi-level inventory matching and order planning under the hybrid Make-To-Order/Make-To-Stock production environment for steel plants via Particle Swarm Optimization［J］.Computers&Industrial Engineering，2015（87）：238-249.