基于Simulink轮边二级减速系统动力学特性分析
路新惠
(河南工业贸易职业学院 机电工程系,河南 郑州 451191)
1 引言
轮边行星减速系统是动力传递减速增扭的重要环节,其安装使用,使矿用自卸车后桥更加紧凑,减小其尺寸,提高车辆的通过性能和整车的装备质量,应用越来越普遍[1]。目前,对齿轮传动所用的静态设计方法逐渐不能适应运行的要求,因而必须采用现代的分析方法和手段。对轮边减速系统的动力学特性研究,重要是建立准确的数学模型和分析方程。对行星齿轮传动系统动力学模型的研究,研究人员多采用纯扭转模型进行分析。文献[2]采用纯扭转建模与平移-扭转耦合动力学建模,通过二者的对比,发现前者的优势更为明显;文献[3]对轮边减速系统进行纯扭转模型建模,并对齿面动载荷进行了分析;文献[4]建立封闭行星齿轮传动系统的动力学分析模型,采用数值解析法多系统在不同激励下的动态响应进行分析。文献[5]在纯扭转模型建模基础上,对模型改进,研究了系统的固有特性。
以电动轮矿用自卸车二级轮边减速器为研究对象,建立二级减速系统动力学模型和方程。首先对行星齿轮传动系统中的非线性因素进行数学描述,进而运用集中质量法建立了纯扭转非线性动力学模型,并在推导了构件相对位移的基础上,运用牛顿力学方程得到运动微分方程。基于Simulink软件建立了二级减速系统模型,模型中包括了扭矩、刚度、阻尼、位移和误差模块。在模型的基础上,分析了负载扭矩、时变啮合刚度、阻尼系数对系统动态特性的影响。
2 二级系统非线性模型和方程
2.1 动力学模型
所研究的电动轮矿用自卸车其路边减速系统为二级系统,其结构模型,如图1所示。系统的动力学模型,如图2所示。

图1 二级轮边减速系统Fig.1 Secondary Wheel Gear System

图2 二级系统动力学模型Fig.2 Dynamic Model
图中:θas、θap、θac、θar—太阳轮、行星轮、行星架、内齿圈的扭转角位移;xas、xap、xac、xar—太阳轮、行星轮、行星架、内齿圈的扭转线位移分别,其值为扭转角位移与标准安装下基圆半径之积;ras、rap、rar—太阳轮、行星轮、内齿圈的基圆半径;rac—行星架半径,其值为太阳轮与行星轮的节圆半径之和,标准安装下亦即太阳轮与行星轮的分度圆半径之和;kasp、casp、basp、easp—太阳轮与行星轮组成的外啮合副的啮合刚度、啮合阻尼系数、齿侧间隙、综合啮合误差;karp、carp、barp、ersp—行星轮与内齿圈组成的内啮合副的啮合刚度、啮合阻尼系数、齿侧间隙、综合啮合误差。
啮合阻尼系数的计算,如式(1)所示。

式中:ζ1、ζ2—外、内啮合副相对阻尼比;ms、mp、mr—太阳轮、行星轮、内齿圈的质量,kg。
2.2 构件相对位移
齿轮结构在啮合线上的相对位移,是组成单元在此方向的线位移的代数和,是准确建模的基础[6],根据图2获得各组成单元的相对位移为:
(1)第一级太阳轮sa1与第一级行星轮pa1沿啮合线方向的相对位移

(2)第一级行星轮pa1与第一级内齿圈ra1沿啮合线方向的相对位移:
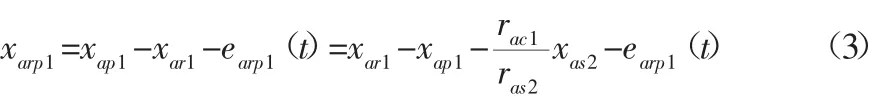
(3)第二级太阳轮sa2与第二级行星轮pa2沿啮合线方向的相对位移

(4)第二级行星轮pa2与第二级内齿圈ra2沿啮合线方向的相对位移:
2.3 运动微分方程
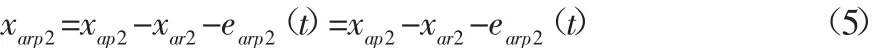
采用牛顿力学方法建立系统纯扭转非线性运动微分方程。对于二级轮边减速行星传动系统,规定输入转矩作用下各个构件产生的运动方向为各自角位移相应的正方向,取θas、θap、θac、ar为广义角坐标。动力从第一级行星传动太阳轮输入,系统的第一个啮合副即为第一级太阳轮与第一级行星轮啮合副。方程输入扭矩为电机输出扭矩Ts,通过第一级太阳轮与第一级行星轮啮合副输出扭矩,另一部分克服第一级太阳轮惯性力。由于系统采用齿轮综合时变刚度所以啮合变形的定义也随之变化,xasp1第一级太阳轮与第一级行星轮啮合变形在齿轮分度圆切向的分量,也就是第一级太阳轮与第一级行星轮啮合点的线位移之差,故,第一个齿轮啮合副的受力平衡方程为:
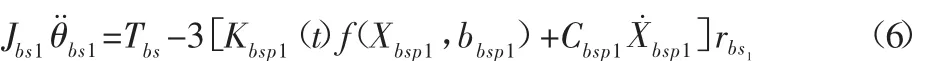
系统第二个齿轮啮合副受到第一级太阳轮的啮合力输入,通过第一级行星轮与第一级内齿圈啮合副输出,同时通过第一级行星架输出扭矩到第二级行星传动,另一部分克服第一级行星轮惯性力:

系统第三个齿轮啮合副为第二级太阳轮与第二级行星轮啮合副,此啮合副受到第一级太阳轮的啮合力、第一级内齿圈啮合力共同通过第一级行星轮经第一级行星架输入第二级太阳轮。这一部分输入经过第二级太阳轮与第二级行星轮啮合副输出啮合力至第二级行星轮,另一部分克服第二级太阳轮惯性力和第一级行星架惯性力[7]。
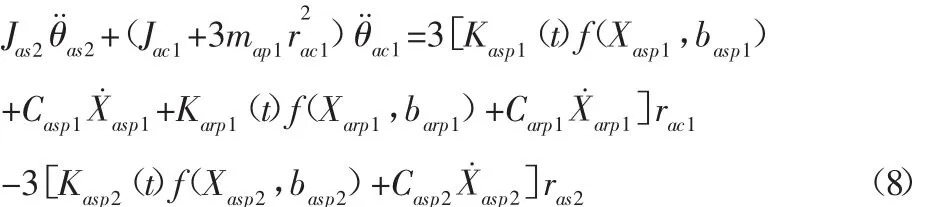
依次类推,系统第四个齿轮啮合副方程为:
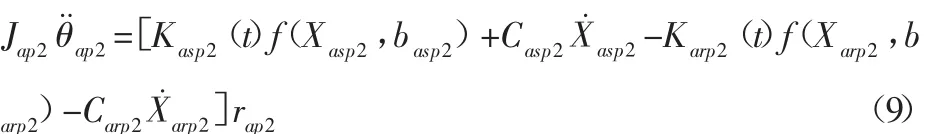
系统第五个齿轮啮合副方程为:

式中:Jas1、Jas2—二级轮边减速器第一、二级太阳轮转动惯量,kg·m2;
Jap1、Jap2—二级轮边减速器第一、二级行星轮转动惯量,kg·m2;
Jac1—二级轮边减速器第一级行星架转动惯量,kg·m2;
Jar12—二级轮边减速器第一、二级内齿圈及连接件等效转动惯量,kg·m2;θar12—二级轮边减速器第一、二级内齿圈及连接件等效扭转角位移;Tas—二级轮边减速器输入转矩,根据具体工况由电机输入,N.m;Tar—二级轮边减速器负载转矩,由车辆行驶阻力计算得出,N.m。
综合式(6)~式(9),建立二级轮边减速行星齿轮系统纯扭转运动微分方程。
2.4 方程无量纲化
定义无量纲时间自变量τ和无量纲激励频率Ω分别为τ=ωant、Ω==ωa/ωan。其中,ωan=(kmasp1/meq1)0.5,meq1=mas1map1/(mas1+map1),kmasp1为第一级太阳轮与行星轮外啮合副刚度均值,ωa为二级轮边减速系统激励频率。

则式(6)~式(9)可以改写为无量纲方程。
3 基于Simulink系统模型
根据数学模型所建立的二级轮边减速器Simulink模型,如图3所示。该模型各有4个矩阵模块、刚度模块、阻尼模块、位移模块和误差分析模块。根据建立的Simulink模型,采用solidworks软件建立了减速器的三维模型。二级轮边减速器主要结构三维,如图4所示。

图3 系统Simulink模型Fig.3 Simulink Model of the System

图4 系统三位模型Fig.4 3D Model of the System
4 参数对系统动态特性的影响
4.1 负载扭矩的影响
根据实际运行中常用工作状况,满载爬坡、满载水平路面、空载运输等三种运行状态,分别取3km/h、25km/h、35 km/h三种情况研究负载扭矩对二级级系统动态特性的影响。二级系统3 km/h时输出扭矩1318758N.m,输入扭矩即电机输出扭矩26323N.m;25km/h 时输出扭矩 158251N.m,输入扭矩 3158.7N.m;35 km/h 时输出扭矩 113036N.m,输入扭矩 2256.2N.m;此时无量纲间隙 b=2,刚度波动系数为 0.2,阻尼系数为 0.03,误差幅值为2[8]。
试验表明,对于第一级太阳轮与行星轮啮合副而言,无量纲间隙从1增大3时,幅值随之减少,而且振动特性变化比较明显;对于第一级行星轮与内齿圈啮合副而言,随着无量纲间隙的增大,啮合副振动的无量纲幅值先减少后增大,振动特性幅值变化明显;对于第二级太阳轮与行星轮啮合副而言,无量纲间隙的增大,啮合副的幅值随着减少,无量纲幅值越大,啮合副在低频区振动情况越复杂;对于第二级行星轮与内齿圈而言,随着无量纲间隙的增大,啮合副幅值随之减少,而且当无量纲的幅值较大时,振动情况越复杂。
综合可知,齿侧间隙存在使系统出现跳跃现象等典型非线性特征。当车辆负载较小时,其为影响系统动力学特性的主要因素;而载荷较小时,其的影响很小。
4.2 时变啮合刚度的影响
由于齿轮副刚度随啮合位置的变化近似呈抛物线形式,取刚度波动系数分别为 0.1、0.2、0.3 三种情况研究时变啮合刚度的影响,此时车速25km/h输出扭矩158251N·m,输入扭矩3158.7N·m,无量纲间隙b=2,阻尼系数0.03,误差幅值为2。
试验表明,对于第一级太阳轮与行星轮啮合副而言,刚度波动系数从0.1增加到0.2时,无量纲幅值随之增加,而且振动跳跃现象更明显复杂,刚度波动系数从0.2增加到0.3时,无量纲幅值随之减少,振动跳跃现象变化不明显;对于第一级行星轮与内齿圈啮合副而言,无量纲幅值随着刚度波动系数的增大,呈现一个先增加后减少的趋势,振动跳跃现象随之复杂并趋于不变;对于第二级来说均与第一级变化类似。综合可知,在系统存在齿侧间隙的情况下,系统均出现了跳跃的现象,说明啮合刚度不能改变系统的冲击特性。
4.3 阻尼系数的影响
对于齿轮传动系统而言,在国际标准单位制下,阻尼比在(10-4~10-1)之间,根据实际润滑方式,这里取阻尼系数ζ=0.01、0.03、0.05三种情况研究阻尼系数对系统动态特性的影响[10]。此时车速25km/h输出扭矩158251N.m,输入扭矩即电机输出扭矩3158.7N.m,无量纲间隙 b=2,刚度波动系数 μ=0.2,误差幅值为 2。
试验表明,对于第一级太阳轮与行星轮啮合副而言,阻尼系数从0.01增加到0.03时,无量纲幅值随之减少,且减少幅值较大,阻尼系数从0.03增加到0.05时,无量纲幅值减少的节奏较慢,变化不明显,而且振动特性情况变化不大;对于第一级行星轮与内齿圈啮合副而言,随着阻尼系数的增大,齿轮副传动的无量纲幅值逐渐减少;对于第二级太阳轮与行星轮啮合副而言,阻尼系数从0.01增加到 0.03,从 0.03 增加到 0.05 时,明显观察出,无量纲幅值逐渐减少;对于第二级行星轮与内齿圈啮合副而言,随着阻尼系数的增大,无量纲幅值随之减少,振动跳跃现象趋于平稳。
5 实验分析
在某款安装有二级行星减速器的车辆进行实测,根据实际运行中常用工作状况,满载工况,车速为20km/h的各级齿轮啮合变形,车速在不同工况下变化时,一级太阳轮-行星轮啮合变形。当车速为20km/h,驱动电机1800转/分时,各级齿轮啮合变形。
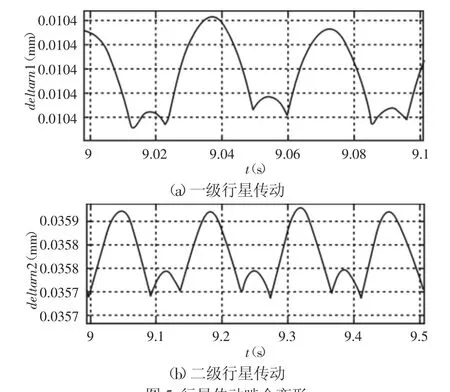
图5 行星传动啮合变形Fig.5 Meshing Deformation of Planetary Transmission
一级太阳轮—行星轮啮合变形,一级行星轮—内齿圈啮合变形如下图,啮合频率784Hz。二级太阳轮—行星轮啮合变形,二级行星轮—内齿圈啮合变形如下图,啮合频率228Hz。
由图可知,轮边减速器在输入转速1800转/分工况下稳定运行时,输入和负载基本不发生变化,齿轮啮合变形大小由齿轮传递的力矩决定,符合轮边减速器传动比规律。齿轮啮合形变在1e-4mm的振幅内波动,波形与齿轮啮合综合时变刚度波形有很强的相似性。但一级太阳轮高速输入端的一级太阳轮—行星轮啮合副啮合变形受电机输入影响为主要因素,只有这一对齿轮的啮合变形出现负值,表明在匀速工况下只有输入齿轮会发生啮合—分离现象。可以推断在多级行星传动稳定地匀速运转时,其中的齿轮副啮合变形大小由它传递的力矩决定,受齿轮啮合时变刚度影响在稳定值周围波动。
当转速为1000r/m、1500r/m、2000r/m时,啮合频率分别为436Hz、653Hz、871Hz时,一级太阳轮—行星轮啮合变形。


图6 一级太阳轮-行星轮啮合变形Fig.6 Meshing Deformation of a Solar Wheel and a Planetary Wheel
由图可知,齿轮同一个啮合副,由于驱动转速增加,齿轮啮合频率增大,齿轮综合时变刚度变化加快,则齿轮啮合变形波形变化也更加明显,当齿轮啮合频率较大时,齿轮啮合变形在较短的时间内呈现于刚度变化相似的波形。当齿轮啮合频率降低时,齿轮啮合综合刚度变化较慢,使得齿轮啮合变形的波动也随之减小。
6 结论
针对矿用自卸车二级轮边减速器,建立二级行星齿轮系统的非线性纯扭转模型,基于运动微分方程搭建二级减速系统Simulink模型。分析了齿轮副的齿侧间隙、时变啮合刚度和综合啮合误差等对系统的动态特性影响变化规律,并通过试验对仿真分析进行了验证。通过分析可知:(1)齿侧间隙的存在使系统出现跳跃现象等典型非线性特征;当系统的负载较小时,其是影响系统动力学特性的主要因素,随负载的增加,其影响逐渐减小。(2)在系统存在齿侧间隙的情况下,系统均出现了跳跃的现象,说明啮合刚度不能改变系统的冲击特性。(3)系统的阻尼系数增加,会伴随着齿轮副穿传动误差的幅值逐渐减小,当前者达到一定的数值时,后者的误差幅值的跳跃现象将会消失。(4)试验分析可知,仿真分析结果的可靠性,二者变化趋势一致,仿真结果可作为优化设计的参考依据。
[1]Guo Y,Parker R G.Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters[J].Journal of Vibration and Acoustics,2010,132(1):1-13.
[2]Dhouib S,Hbaieb R,Chaari F.Free vibration characteristics of compound planetary gear train sets[J].Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science,2008,222(8):1389-1401.
[3]Kiracofe D R,Parker R.G.Structured vibration modes of general compound planetary gear systems[J].ASME Journal of Vibration and Acoustics,2007,129(1):1-16.
[4]Parker R.A.Mesh phase relations of general compound planetary gears[C].Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York,N.Y.American Society of Mechanical Engineering,2007(7):631-646.
[5]刘守法,连莹.154吨电动轮自卸车轮边减速器的设计与分析[J].机械设计与制造,2011(2):36-37.(Liu Shou-fa Lian Ying.Design and analysis of wheel-side reducer for 154T motor clump trucks[J].Machinery Design&Manufactur,2011(2):36-37.)
[6]李同杰,朱如鹏,鲍何云.行星齿轮系扭转非线性振动建模与运动分岔特性研究[J].机械工程学报,2011,47(21):76-83.(Li Tong-jie,Zhu Ru-peng,Bao He-yun.Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear Train[J].Journal of Mechanical Engineering,2011,47(21):76-83.)
[7]刘文吉,宋朝省,洪英.NN型少齿差行星齿轮传动啮合冲击分析及修形设计[J].中国机械工程,2012,23(4):425-429.(Liu Wen-ji,Song Chao-xing,Hong Ying.Meshing impact analysis and profile modification of planetary gear drive with small tooth number difference[J].China Mechanical Engineering,2012,23(4):425-429.)
[8]孙智民,季林红,沈允文.2K-H行星齿轮传动非线性动力学[J].清华大学学报:自然科学版,2003,43(5):636-639.(Sun Zhi-min,Ji Lin-hon,Shen Yun-wen.Nonlinear dynamics of 2K-H planetary gear train[J].Journal of Tsinghua University:Science and Technology,2003,43(5):636-639.)

