典型构件疲劳微裂纹全寿命预测方法研究

孙志礼，柳溪溪，柴小冬，于 瀛

（东北大学 机械工程与自动化学院，辽宁 沈阳 110819）

1 引言

疲劳失效是机械设备中零件的主要失效形式之一，对于电子工程、航空航天、光学、军事等领域中的设备，要求有较高的精度，而设备中关键零件或构件的力学性能和使用寿命，很大程度上受到疲劳产生的微裂纹、微缺陷的影响，某个关键构件的失效可能会导致整个设备无法正常工作，进而影响生产，造成经济损失。因此，为确保机械设备的可靠运行，准确地预测关键构件中裂纹形成及扩展寿命，在工业生产中有着重要的意义[1]。

一般情况下，机械结构疲劳失效过程主要分为裂纹形成和裂纹扩展两个阶段，并分别采用不同的方法独立地分析两个阶段。裂纹形成阶段用到的是实验的方法以及实验与统计经验相结合的方法，而裂纹扩展阶段主要用到断裂力学的理论[2]。虽然概念上两个阶段不同，从量上看两阶段的界限模糊不清，计算过程中无法很好地定义两者之间的界限。断裂力学模型则无法描述出零件表面微缺陷或裂纹的形成及其发展对宏观力学性能的影响。实际上，从损伤力学的角度来看，裂纹形成、裂纹扩展是连续损伤演化的过程，可以将两个阶段统一起来研究。应用损伤力学，主要研究材料内部微缺陷的产生及发展所引起的宏观上的力学效应，其理论描述了由于微裂纹的发展导致材料破坏的过程和规律。目前，已有学者根据损伤力学相关理论研究出将裂纹萌生与裂纹扩展统一计算的模型，并且已经应用在了一些领域里[3-5]。但这些模型普遍应用的范围较窄，并且没有给出微观损伤过程中单个单元损伤的演化。

针对现有方法的不足，根据损伤力学理论以及有限元方法，构建求解疲劳寿命的统一模型，计算过程中引入了附加载荷法[6]，通过连续计算损伤后各阶段的刚度矩阵，分析了微观上单元损伤的劣化过程，同时简化了计算过程，给出了疲劳微裂纹损伤模型，并通过理论计算结果与试验结果做对比，验证了方法的可行性。

2 模型的建立

根据损伤力学理论建立疲劳寿命计算模型的基本思路为：选取合适的损伤变量实现对材料微结构劣化过程的描述；建立损伤演化方程，反映材料内部损伤的变化规律；建立损伤本构方程，求解计入损伤后的应力场、位移场、应变场[7]。

2.1 损伤因子及损伤演化方程的引入

损伤力学中以损伤因子D来反映材料的劣化过程[8]：

式中：E—无损状态的弹性模量；E′—处于损伤状态的弹性模量。

一般来说，材料无损状态时D=0，材料完全损伤时D=1。将D的值作为材料破坏与否的判定。

将损伤变量引入到本构方程中：

式中：参数β反映了耦合的程度，取值0≤β≤1。

对于单轴加载的情况，将加载等效为当量损伤驱动力，结合损伤驱动力门槛值，损伤演化方程可表示为[9]：

式中：σmax—受载荷最大时对应的单元等效应力；R—应力比；q—材料常数；α，p—材料参数，由材料的中值疲劳曲线确定；σth0—材料无损状态的应力门槛值。

2.2 附加载荷的计算

由于损伤的存在，使得材料刚度出现变化，为直观地反映这一变化，将本构方程中损伤因子存在的部分看作附加力，将其引入到有限元方程中可以得到：

式中：K—总体刚度矩阵；δ—单元节点的位移；f—所施加外力；

式中：Kk—各单元刚度矩阵的扩展矩阵；Dk—各单元的损伤度。

2.3 模型计算过程

结合损伤理论和有限单元法，进行疲劳寿命的计算，取试件初始损伤为，上标代表危险单元的编号，取0时，代表第一个危险单元的计算过程，下标为计算单个危险单元寿命的循环次数，x为单元序号。模型计算过程如下：

（1）对所选试件进行静力分析，得到各单元等效应力，将等效应力最大的单元作为危险单元，记最大等效应力为σMe。

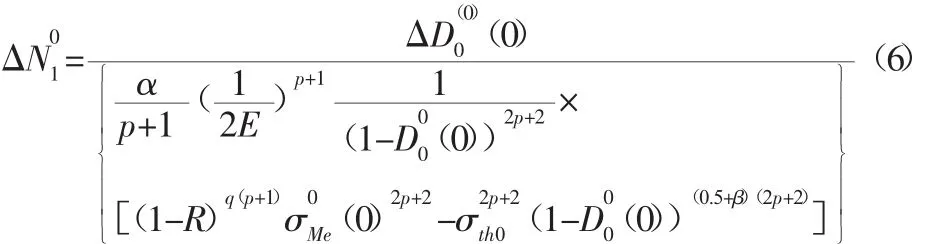
（3）根据危险单元的损伤步长确定各单元的损伤步长：

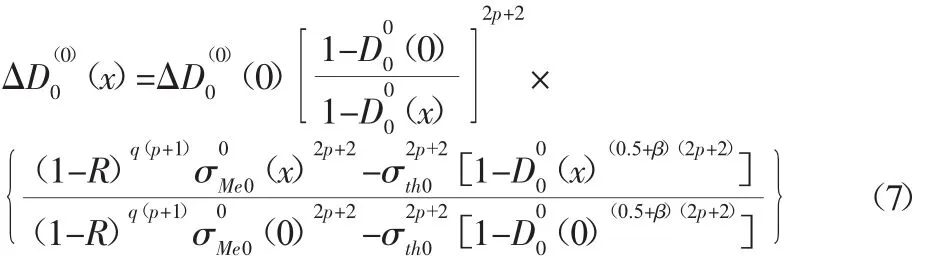
（4）由步骤（1）～（3），可得危险单元前进一个步长下各单元损伤度的大小

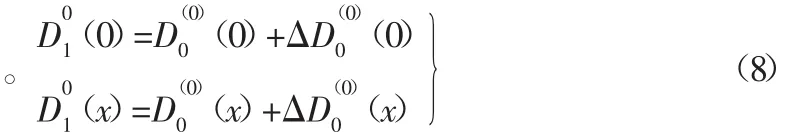
（5）由附加载荷法计算各单元的等效应力，得到危险单元的等效应力 σ0Me1，重复步骤（2）～（4），直至 D0（0）=1 为止，此时危险单元完全破坏，危险单元寿命为：

N0即为裂纹萌生寿命，由步骤（1）～（5）循环已经得到了各单元损伤度D0（x），选取损伤度次小的单元进行寿命计算，依次得到其余危险单元的寿命，直至试件发生断裂，裂纹形成与扩展总体寿命为

式中：L—危险单元的序号。

3 程序的编写流程

采用matlab软件对计算过程进行编程，程序的设计流程，如图1所示。

图1整体计算流程Fig．1 The Whole Calculation Process

图1 中初始条件包括材料的参数以及对所分析试件有限元模型网格划分后各单元编号和各节点坐标。D为危险单元损伤度。输出结果包括试件寿命，单元破坏的顺序及编号。

4 损伤模型的验证

4.1 有限元模型及其相关参数

以文献[10]中疲劳试验数据为依据，算例采用LY4高强度铝合金钢板中的两种试件，对试件轴向加载，试验频率为（110～130）Hz。试件1材料参数及应力比，如表1所示。

建立相应模型1，网格划分，如图2所示。

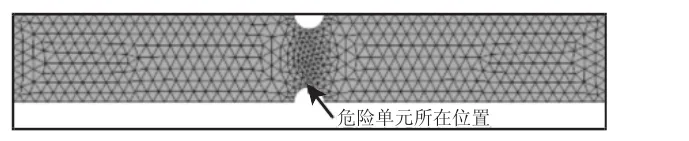
图2 模型1的网格划分Fig．2 Meshing of the First Model

将缺口处的网格进行细化分，将划分结果以及材料参数导入程序中进行计算，得到的第一个危险单元为972号单元，位于缺口边缘位置。

模型2的材料参数及应力比，如表2所示。建立相应的模型2，网格划分，如图3所示。

表2 试件2的损伤参数表及应力比Tab.2 The Damage Parameter and Stress Ratio of Second Sample

图3 模型2的网格划分Fig．3 Meshing of the Second Model

同样，在宽度较小的区域进行网格的细划分，第一个危险单元为1406号单元，出现在宽度最小的边缘位置。

4.2 单元的损伤演化分析

为分析单个单元等效应力变化，以模型1的计算为例，根据危险单元寿命的计算结果，列出各步长对应的载荷循环次数，以第一个危险单元为研究对象，在最大应力为150MPa时计算得到972号单元的损伤演化，如图4所示。

图4 各损伤步长对应的载荷循环次数Fig．4 The Frequence of Cyclic Loading in Every Step

由图4可见，载荷循环次数呈现为先增大后减小的趋势，在材料参数及加载确定的情况下，其数值与单元等效应力和损伤度有关。当步长前进到18的时候，开始出现波动，初步认为出现波动的原因是对应的载荷出现波动，由此观察各损伤步长下载荷的变化图形，如图5所示。

图5 各损伤步长下对应危险单元的等效应力Fig．5 The Equivalent Stress of Dangerous Element in Every Step

由图5可见，步长前进到18后，危险单元等效应力出现波动，验证了图4载荷循环次数的波动。此时认为危险单元在前18次循环作为主要承载力的单元，而18次循环后，由于损伤累积，承载能力相对其它单元较快减小，微观上，与相近单元交替作为主要承载力的单元。循环35次后，危险单元承载的力急剧减小，（35～100）次循环间，承载力逐步减为0，表明危险单元损伤因子累积为1后破坏，失去承载能力，由此描述了试件微结构的损伤演化过程。

4.3 计算结果的对比

根据式（10），计算不同载荷条件下试件的总体寿命，计算结果，如表3所示。

表3 试件1疲劳寿命的计算结果Tab.3 The Calculated Results of the First Sample’s Fatigue Life

由表3可见，试件1的疲劳寿命随所施加载荷的增大而减小。同样计算得到试件2的疲劳寿命，并将计算结果与试验结果作对比，绘制成曲线图，如图6、图7所示（图中虚线代表的是由试验数据拟合的计算结果，点代表的是试验点，实线为应用计算模型计算得到的结果）。

图6 试件1计算结果与试验结果的对比Fig．6 Comparison of Calculated and Experimental Results of First Sample

图7 试件2计算结果与试验结果的对比Fig．7 Comparison of Calculated and Experimental Results of Second Sample

由图6、图7可见，试件的疲劳寿命均随所施加载荷的增大而减小，计算结果与试验结果存在误差，误差的出现是计算过程中损伤参数的确定存在一定的偏差，也可能为试验本身存在误差。进一步计算相对误差在10%以内，在可接受范围内，可视为计算结果与试验结果基本吻合，验证了疲劳裂纹损伤模型的正确性；通过采用多个试件进行计算验证，说明了计算模型具有较好的适用性。

5 结论

应用损伤力学理论建立疲劳裂纹损伤模型，以LY4铝合金板材为例进行裂纹萌生及扩展寿命计算，通过对比试验结果分析，得出以下结论：

（1）单个单元在损伤演化过程中，等效应力呈现为先增大后减小的趋势，对于金属材料，单元的等效应力在材料损伤过程会呈现一定的跳动变化，最后逐渐减为0，而单元的承载能力则一直呈衰减趋势。

（2）两组试件的疲劳寿命均随所施加载荷的增大呈减小的趋势。

（3）将统一模型应用到轴向加载的金属板件上，误差在可接受范围内，可以准确地预估单轴加载板件的寿命，对于研究金属材料微观尺度上损伤演化具有重要的参考意义。

［1］郝琪.多轴疲劳寿命预测方法研究［J］.机械设计与制造，2010（12）：122-124.（Hao Qi.The study on multiaxial fatigue life prediction approach［J］.Machinery Design ＆ Manufacture，2010（12）：122-124.）

［2］李爱民，崔海涛.基于非线性连续介质损伤力学方法的微动疲劳寿命预测［J］.航空学报，2013，34（19）：2122-2129.（Li Ai-min，Cui Hai-tao.Prediction of fretting life based on nonlinear continuum damage mechanics［J］.Acta Aeronautica et Astronautica Sinica，2013，34（19）：2122-2129.）

［3］张淼，邹希.谐振载荷作用下工程结构振动疲劳寿命预估的损伤力学-有限元法［J］.计算力学学报，2010，27（5）：948-952.（Zhang Miao，Zou Xi.Damage mechanics-finite element method for vibration fatigue life prediction of engineering structures under resonant loading［J］.Chinese Journal of Computational Mechanics，2010，27（5）：948-952.）

［4］Melanie Fiedler，Michael Vormwald.Considering fatigue load sequence effects by applying the local strain approach and a fracture mechanics based damage parameter［J］.Theiretical and Applied Fracture Mechanics，2016（83）：31-41.

［5］Vuong Nguyen Van Do.High cycle fatigue analysis in presence of residual stresses by using a continuum damage mechanics model［J］.International Journal of Fatigue，2015（70）：51-62.

［6］董赟，蔡敢为.基于损伤力学的疲劳寿命和裂纹扩展的数值分析［J］.中国机械工程，2010，21（20）：2412-2415.（Dong Bin，Cai Gan-wei.Numerical analysis of fatigue life and crack growhbased on damage mechanics［J］.China Mechanical Engineering，2010，21（20）：2412-2415.）

［7］刘新东，郝际平.连续介质损伤力学［M］北京：国防工业出版社，2011：126-128.（Liu Xin-dong，Hao Ji-ping.Continuum Damage Mechanics［M］.Beijing：National Defense Industry Press，2011：126-128.）

［8］张彦军，张淼.基于损伤力学方法的带板连接件疲劳寿命预估［J］.机械强度，2011.33（3）：443-449.（Zhang Yan-jun，Zhang Miao.Fatigue life prediction of the joint plate based on damage mechanics method［J］.Journal of Mechanical Strength.2011，33（3）：443-449.）

［9］张行.断裂与损伤力学［M］.北京：北京航空航天大学出版社，2006：511-522.（Zhang Hang.Fractureand Damage Mechanics［M］.Beijing：Beihang University Press，2006：511-522.）

［10］高镇同.疲劳性能试验设计和数据处理［M］.北京：航空航天大学出版社，2008：65-89.（Gao Zhen-tong.The Data Processing and Design of Fatigue Property Experiment［M］.Beijing：Beihang University Press，2008：65-89.）