应力水平对桥机金属结构优化及可靠性的影响
陶元芳,叶青林,范小宁,师 玮
(太原科技大学 机械工程学院,山西 太原 030024)
1 引言
桥机金属结构优化设计往往只追求结构轻量化,其最优解常常把强度、刚度和稳定性的许用值用到极限,这样做不能确保结构是否安全,而工程设计人员一般都留有一定的设计裕度[1]。而实际工程设计中,一般留有一定的安全裕度,而不采用优化设计的最优解。引入了应力水平来定量的衡量设计裕度,如式(1)所示,用可靠度来衡量结构是否安全。通过采用不同的设计裕度,分别对桥机金属结构进行优化设计,并对优化结果进行可靠性分析,研究了应力水平对桥机金属结构优化设计及可靠性的影响。

式中:σ—广义设计应力,表示危险截面验算点强度、刚度、稳定性的实际值;[σ]—广义许用应力,表示强度许用值、刚度许用值、稳定性许用值;η—广义应力水平,表示设计时广义许用应力的最大使用比例。
2 桥机金属结构的优化设计模型
2.1 设计变量
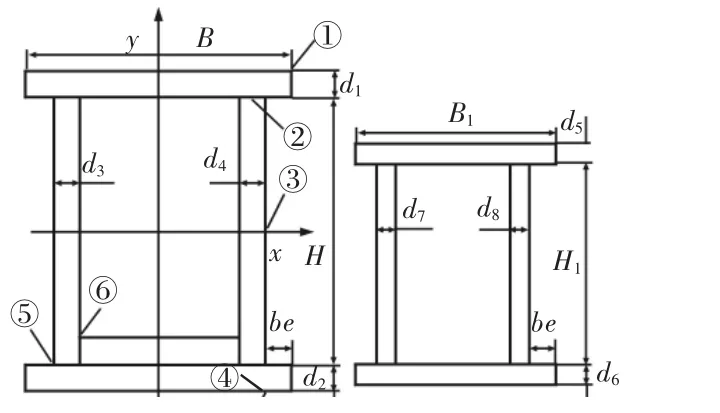
图1 主梁、端梁截面简图Fig.1 The Section Diagram of Main Girder and End Girder
以主梁和端梁截面参数作为设计变量,如图1所示,共有12个设计变量:主梁翼缘板宽度B、主梁上翼缘板厚度d1、主梁下翼缘板厚度d2、主梁主腹板厚度d3、主梁副腹板厚度d4、主梁腹板高度H,端梁上翼缘板厚度d5、端梁下翼缘板厚度d6、端梁左腹板厚度 d7、端梁右腹板厚度d8、端梁腹板高度H1。定义向量X为所有设计变量组成的向量,则:X=(d1,d2,d3,d4,H,B1,d5,d6,d7,d8,H1)
2.2 约束条件
2.2.1 主梁约束条件
设垂直载荷与水平载荷在主梁第i(i=1,2,…,6)个验算点的应力分别为 σix、σiy。
(1)静强度约束。主梁跨中①点最大自由弯曲正应力约束:

主梁跨中②点最大约束弯曲正应力约束:主梁跨端③点最大切应力约束:
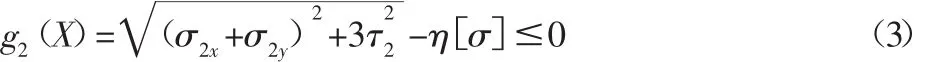

式中:Fc1—腹板上的垂直剪切力;Tn—水平惯性力引起的扭矩;hd—主梁跨端处腹板高度;A0—主梁跨端截面面积。
④点同时有约束弯曲和约束扭转:
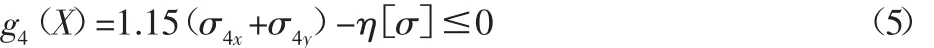
(2)疲劳强度约束,起重机整机工作级别A5以上对应结构工作基本E4以上要进行疲劳强度校核[2]。
主腹板受拉翼缘焊缝⑤点疲劳强度约束:

式中:[σr]—疲劳许用应力与工作级别有关。
大隔板下端与腹板连接的焊缝⑥点疲劳强度约束:
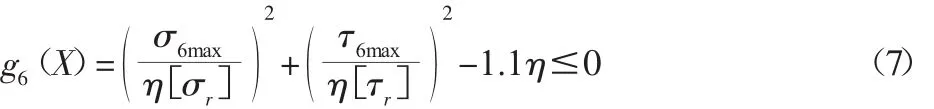
式中:σ6max、τ6max—载荷组合A计算的大隔板下端与腹板相连接
的焊缝存在较大的拉应力和切应力。
(3)主梁刚度约束,主梁跨中静挠度约束:
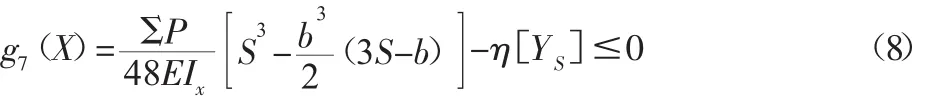
式中:ΣP—移动集中载荷之和;S—桥架跨度;b—小车轮距;[YS]—许用静挠度。
主梁垂直动刚度约束,以满载小车位于跨中时产生的垂直自振频率来表征桥架主梁的动刚度。

式中:y0—额定起升载荷点产生的静位移;λ0—额定起升载荷对钢丝绳产生的静位移;β—结构质量影响系数;[fV]—自振频率控制值,一般可取2MHz。
(4)主梁稳定性约束,主梁整体为稳定性要求高宽比不超过3。
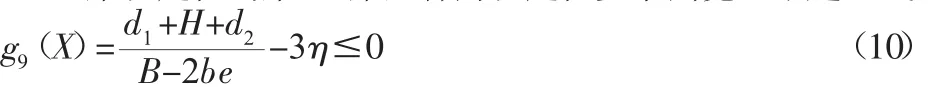
2.2.2 端梁约束条件
(1)静强度约束,1-1截面应力约束。
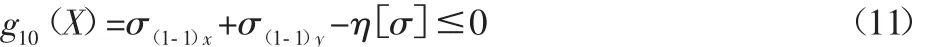
式中:σ(1-1)x、σ(1-1)y—垂直载荷与水平载荷在 1-1 截面角点的应力。
2-2截面主、端梁搭接处应力约束:

式中:σ2-2x、σ2-2y—垂直载荷与水平载荷在2-2截面角点的应力。
3-3截面由垂直载荷作用的剪力在腹板上产生的剪应力:

式中:Fdc—3-3截面垂直剪切力;
Sdx—验算点以上截面对x轴的静距。
(2)稳定性约束,端梁整体为稳定性要求高宽比不超过3。
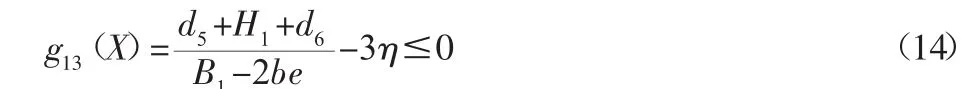
(3)工艺尺寸约束。
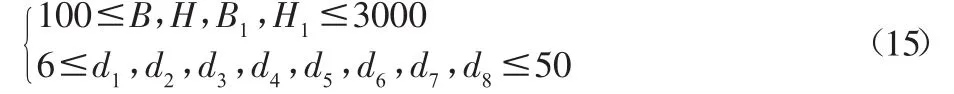
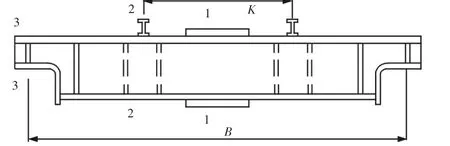
图2 端梁截面示意图Fig.2 The Section Diagram of End Grider
2.3 目标函数
以桥机金属结构的质量作为目标函数,对于双梁桥机金属结构,可按下式计算:f(X)=2(G主梁+G端梁) (16)式中:G主梁—一根主梁的质量;G端梁—一根端梁的质量。
2.4 优化算法
粒子群算法本身是一种基于群智能的随机无约束优化算法,但是通过结合惩罚函数法对粒子群算法进行改进可以有效解决约束优化问题,并且这种算法实现容易,精度高,收敛快[3]。
3 桥机金属结构的可靠性分析
3.1 不确定因素及其分布统计
影响桥机金属结构可靠度的不确定因素主要包括:起升载荷的不确定性,材料参数的不确定性,加工制造过程引起的几何尺寸的不确定性等。在随机可靠性分析中,可用概率模型来描述不确定性因素[4]。定义表征影响桥机结构可靠性的不确定性的基本随机变量为 X′,则:X′=(P,σs,E,B,d1,d2,d3,d4,H,B1,d5,d6,d7,d8,H1)
3.1.1 起升载荷的不确定性模型
桥式起重机的起升载荷可认为近似服从截尾正态分布,一些服从威布尔分布规律的载荷在一定条件下也可以用正态分布来近似[3]。起升载荷 P~N(μp,σ2p)且 P⊂[0,PQ]。其中,μp为起升载荷均值,μp=aPQ;σp为起升载荷标准差,σp=bμp;PQ为额定起升载荷;a、b为起升载荷均值系数、起升载荷变异系数,与起重机金属结构工作级别有关,可以根据实测数据或者经验值推算得到。
3.1.2 材料参数的不确定性
(1)材料的屈服极限。起重机金属结构常使用塑性材料Q235和Q345,用达到屈服极限强度来表征材料发生破坏。在做可靠性分析或设计时,需要对所用的钢材做实验来估计材料屈服极限的分布,如没有实验数据,可近似认为材料的强度基本可用正态分布来描述,可以取屈服极限均值=1.1σs,变异系数[5]Vs=0.07。对于Q235,屈服极限均值=258.5MPa,标准差Sσ=18.095MPa。(2)材料的弹性模量。钢材的弹性模量可以认为服从正态分布。钢材的弹性模量均值=2.06×105MPa,变异系数 VE=0.03,标准差 SE=VE6.18×103MPa。(3)材料板厚的不确定性。GB/T 709—2006 对热轧钢板的板厚的允许偏差进行了详细规定,然而实际工程上应用的钢板却与标准不符。我国绝大部分起重机所用的钢板使用负偏差,有些负偏差甚至达到公称厚度的7%[6]。为了研究方便,以正态分布来描述钢板板厚的分布,设钢板厚度的公称尺寸为δ,上偏差为0,下偏差为 Δδ,根据“3σ”原则,板厚的均值δ¯=(δ-Δδ)/2,标准差 Sσ=Δδ/6。由此可以得到主梁和端梁截面参数(d1~d8)的分布规律。
3.1.3 加工过程引起的几何尺寸的不确定性
一般认为由加工制造过程引起的几何尺寸的不确定性服从正态分布,仍旧按照“3σ”原则,根据公称尺寸和上下偏差求出各几何尺寸的最大值 xmax和最小值 xmin,则均值x¯=(xmax+xmin)/2,标准差Sx=(xmax-xmin)/6。由此可以得到主梁和端梁截面参数B,H,B1,H1的分布。
3.2 桥机结构主要失效模式
根据桥机金属结构的载荷特点和优化设计数学模型,提出桥机金属结构系统3S((强度、刚度、稳定性)失效准则,根据失效准则可以确定相应的失效模式[7]。(1)主梁静强度失效:主梁危险点①~④处超过许用值,则认为失效,共有四种失效模式。(2)主梁疲劳强度失效:主梁危险点⑤、⑥处应力超过疲劳应力许用值,则认为失效,共有两种失效模式。(3)主梁刚度失效:主梁跨中静挠度达到许用静挠度,或主梁满载自振频率未达到自振频率控制值,共有两种失效模式。(4)主梁稳定性失效:金属结构高宽比超过3,则认为失效,共有一种失效模式。(5)端梁强度失效:端梁危险截面1-1、2-2、3-3处应力超过许用值,则认为失效,共有三种失效模式。(6)端梁稳定性失效准则:端梁高宽比超过3,则认为失效,共有一种失效模式。
桥机金属结构的各失效模式均以是否满足3S(强度、刚度、稳定性)要求来判定,与优化设计中的约束条件一致。优化设计中的第 k(k=1,2,…,13)个约束条件 gk(X)取应力水平 η=1,同时把确定性变量变成服从一定概率分布的不确定变量[8],可转化成相应的失效模式的功能函数。桥机金属结构失效树,如图3所示。桥机金属结构各失效模式间是“或门”关系,即任一失效模式的发生均会引起桥机金属结构的失效,且各基本事件Gk(X)>0(k=1,2,…,13)之间存在相关性。
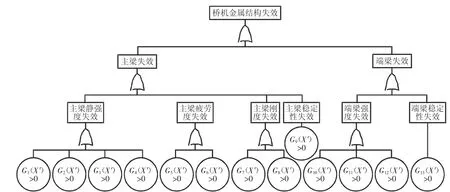
图3 桥机金属结构失效树Fig.3 Fault Tree of Overhead Traveling Crane Metal Structure
3.3 桥机金属结构可靠性分析方法
结构系统一般存在多种失效模式,而且各失效模式之间之间存在相关性。此外,结构各失效模式极限状态方程一般为隐式的非线性方程,不利于直接求解。Monte Carlo法是一种被公认的相对精确且简单通用的可靠性分析方法[9-10]。借助计算机可以产生服从任意概率分布的随机数,且模拟次数N越大,失效概率Pf的模拟值与真实值的误差越小,一般建议95%的置信度保证Monte Carlo法的误差足够小,N必须满足N≥100/Pf[10]。
4 实例分析
为了研究应力水平这一设计裕度对桥机金属结构优化设计及可靠性的影响,利用面向对象的软件开发方法,以VC++6.0为开发工具,编制了桥机金属结构优化设计和可靠性分析软件。利用编制的软件,通过改变应力水平,对桥机金属结构进行优化设计,然后对优化结果采用Monte Carlo法进行可靠性分析,记录数据,绘制曲线变化曲线。实例分析一:80t/28m中轨双梁桥机金属结构,工作级别 E7,影响结构可靠度的基本随机变量 X′=(P,σs,E,B,d1,d2,d3,d4,H,B1,d5,d6,d7,d8,H1)T各参数均服从正态分布,分布参数分别为:起升载荷均值系数0.80,变异系数0.30,起升载荷均值 E(Q)=0.8×80t=64t,起升载荷标准差 σ(Q)=0.3×E(Q)=19.2t;材料为 Q235,屈服极限均值 σs=258.5MPa,标准差 Sσ=18.095MPa;抗弯弹性模量均值 E=2.06×105MPa,标准差 SE=6.18×103MPa;钢板厚度 d1,d2,d3,d4,d5,d6,d7,d8正偏差取 0,负偏差取0.5mm;截面参数 B,H,B1,H1正偏差取 5mm,负偏差取 5mm。应力水平从70%到120%间隔5%进行一次优化设计,将得到的最优解采用蒙特卡罗法计算可靠度。保证蒙特卡罗法求解可靠度的精度达到10-4,模拟次数应为N=106,将采集的样本数据记录,如表1所示。根据表1中样本数据绘制变化曲线,如图4所示。
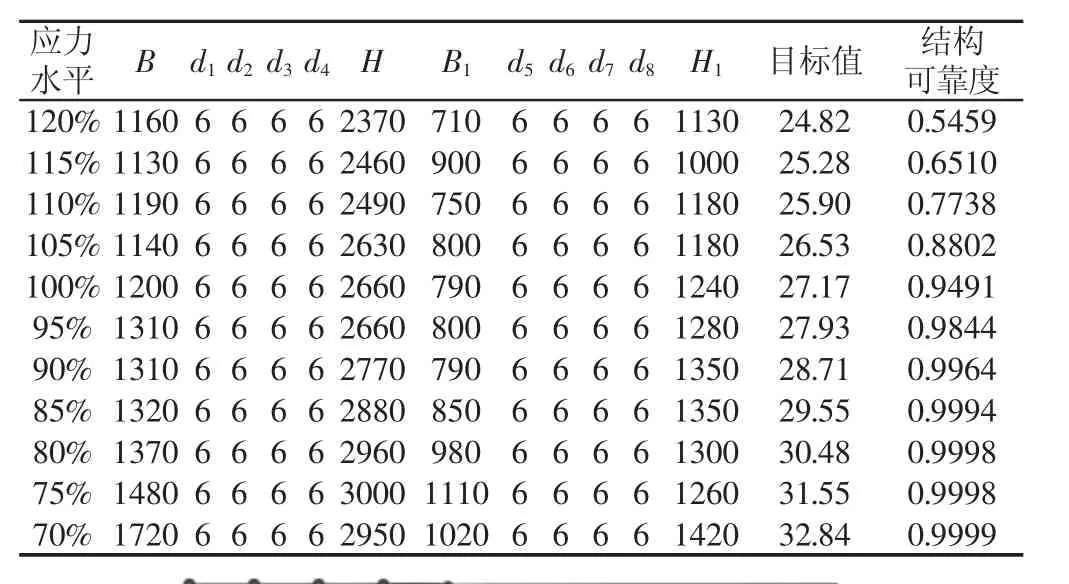
表1 80t/28m(E7)桥机金属结构样本数据Tab.1 80t/28m(E7)Overhead Traveling Crane Metal Structure Sample Data
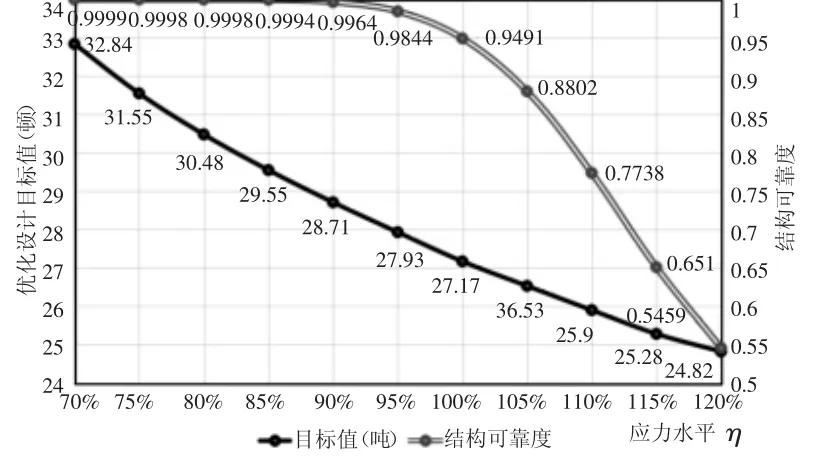
图4 80t/28m(E7)桥机金属结构样本数据变化曲线Fig.4 80t/28m(E7)Overhead Traveling Crane MetalStructure Sample Data Changing Curve
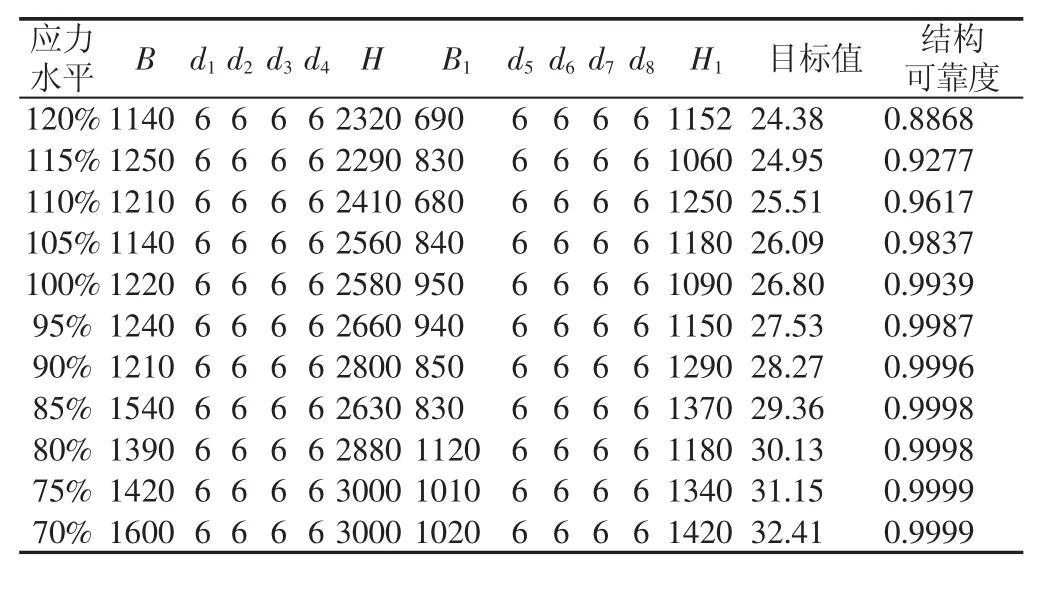
表2 80t/28m(E7)桥机金属结构样本数据Tab.2 80t/28m(E7)Overhead Traveling Crane Metal Structure Sample Data
实例分析二:80t/28m中轨双梁桥式起重机,工作级别E5,影响结构可靠度的基本随机变量 X′=(P,σs,E,B,d1,d2,d3,d4,H,B1,d5,d6,d7,d8,H1)T各参数均服从正态分布,分布参数分别为:起升载荷均值系0.50,变异系数0.50,起升载荷均值E(Q)=0.5×80t=40t,起升载荷标准差 σ(Q)=0.5×E(Q)=20t;其他参数与实例分析一相同。样本采集方法与实例分析一相同,将采集的样本数据记录,如表2所示。根据表2中数据绘制变化曲线,如图5所示。

图5 80t/28m(E5)桥机金属结构样本数据变化曲线Fig.5 80t/28m(E5)Overhead Traveling Crane Metal Structure Sample Data Changing Curve
5 结论
(1)应力水平与桥机结构的优化设计目标函数(金属结构重量)近似成线性关系。随着应力水平的提高,金属结构重量均可近似线性递减。(2)随着应力水平降低,结构的可靠度不断提高,但提高的幅度越来越小,可分为三个阶段:变化较快阶段、缓慢变化阶段和近似不变阶段。在变化较快阶段,随着应力水平的降低,结构的可靠度近似成线性不断提高;在缓慢变化阶段,随着应力水平的降低,结构的可靠度也在提高,但变化的幅度远不如变化较快阶段;在近似不变阶段,随着应力水平的降低,结构的可靠度的提高量微乎其微几乎不变,在变化曲线上近似一条无限趋向于1的水平直线,即提高换取较高可靠度的回报率越来越低。(3)不能盲目的追求结构的可靠度而过度的降低应力水平,也不能盲目的追求结构轻量化而过度的提高应力水平。适当的提高应力水平,即留有一定的设计裕度,使结构的可靠度在缓慢变化阶段,既可以减轻金属结构的重量,也可获得较高的可靠性水平。做起重机的金属结构设计时,应力水平一般不能超过100%,推荐选90%左右。(4)同等应力水平、相同起重量的桥机金属结构,工作级别高的可靠度要偏低。做金属结构设计时,工作级别高的起重机应选择相对较低的应力水平,即需要留有更大的设计裕度;在其他条件一致的前提下,结构的可靠性主要受工作级别也就是起升载荷分布参数的影响。
[1]Hee Youb Kang,Byung Man Kwak.Application of maximum entropy principle for reliability-based design optimization[J].Structural and Multidisciplinary Optimization,2009(4).
[2]张质文,虞和谦,王金诺.起重机设计手册[M].北京:中国铁道出版社,2013:75-77.(Zhang Zhi-wen,Yu He-qian,Wang Jin-nuo.Crane Design Handbook[M].Beijing:China Railway Press,2013:75-77.)
[3]叶青林,陶元芳.粒子群算法结合惩罚函数法用于桥式起重机金属结构优化[J].起重运输机械,2015(4):46-49.(Ye Qing-lin,Tao Yuan-fang.Particle Swarm Optimization combined with SUMT for main girder design of overhead traveling crane[J].Hoisting and Conveying Machinery,2015(4):46-49.)
[4]张义民,孙志礼.机械产品的可靠性大纲[J].机械工程学报,2014(14):14-20.(Zhang Yi-min,Sun Zhi-li.The reliability syllabus of mechanical products[J].Journal of Mechanical Engineering,2014(14):14-20.)
[5]闻邦椿.机械设计手册[M].北京:机械工业出版社,2010:4150-4170.(Wen Bang-chun.Mechanical Design Manual[M].Beijing:Mechanical Industry Press,2010:4150-4170.)
[6]喻颖.起重机械制造用钢板负偏差问题的探讨[J].起重运输机械,2012(3):98-100.(Yu Ying.Discussion on the negative deviation of steel plate for hoisting machinery manufacture[J].Hoisting and Conveying Machinery,2012(3):98-100.)
[7]杨瑞刚,徐格宁,范小宁.桥式起重机结构可靠性失效准则与剩余寿命评估准则[J].中国安全科学学报,2009(10):95-100.(Yang Rui-gang,Xu Ge-ning,Fan Xiao-ning.Reliability failure criterion and residual life assessment criteria for overhead traveling crane structure[J].China Safety Science Journal,2009(10):95-100)
[8]唐家银,何平,赵永翔.应力-强度相关性干涉下的随机安全系数与零件可靠性设计[J].机械设计与制造,2011(12):16-18.(Tang Jia-yin,He Ping,Zhao Yong-xiang.Random safety factor and component reliability design with interference of correlation of stress-strength[J].Machinery Design&Manufacture,2011(12):16-18.)
[9]安伟光,赵维涛,安海.随机结构系统综合考虑静强度、刚度和疲劳的多失效模式的可靠性分析[J].中国科学,2009,37(4):516-526.(An Wei-guang,Zhao Wei-tao,An Hai.The reliability analysis of the multiple failure modes of the stochastic structural system considering the static strength,stiffness and fatigue[J].Science in China,2009,37(4):516-526.
[10]Kalbfleisch J D,Lawless J F.Estimation of reliability in field performance studies[J].Technometrics,1988(30):365-378.

