广义Birkhoff系统的分离变量与局部能量积分

张 毅

（苏州科技大学 土木工程学院，江苏 苏州 215011）

研究动力学方程的第一积分有重要意义。如果能够找到若干积分，便对力学系统的动力学行为有所了解；如果能够找到全部积分，也就找到了问题的解。Whittaker在其著作[1]中讨论了一类完全可积的完整保守系统，其广义坐标全部为分离坐标，相应地系统有n个局部能量积分。Liouville将结果进行了推广：凡力学系统的动能和势能可以写成某种形式，则该力学系统可以分成单积分的形式来求解[1-3]。文献[4]从广义Chaplygin方程出发，将局部能量积分的理论推广到一类非完整保守系统。文献[5]初步研究了Birkhoff系统的局部能量积分。关于约束力学系统的分离变量和局部能量积分的研究尚不多见。

广义Birkhoff系统是Birkhoff系统的推广。在Birkhoff方程的右端增加一个附加项成为广义Birkhoff方程。由于附加项的调节作用，构造广义Birkhoff系统比Birkhoff系统更容易，非保守和非完整力学系统都可以直接纳入广义Birkhoff系统，因此，对广义Birkhoff系统动力学的研究具有重要意义[6-16]。笔者将研究广义Birkhoff系统的分离变量与局部能量积分问题，分别讨论分离变量为单变量和耦合的两个变量情形下，存在局部能量积分的条件及其形式，并将结果应用于Birkhoff系统。文中给出相应的算例以说明结果的应用。

1 分离变量为单变量时系统的局部能量积分

研究由 2n 个变量 aμ（μ=1，2，…，2n）描述的广义 Birkhoff系统。 设 Birkhoff函数为 B=B（t，av），Birkhoff函数组为 Rμ=Rμ（t，av），附加项为 Λμ=Λμ（t，av），则广义 Birkhoff方程为[6]

如果有一个Birkhoff变量，例如aj，可在Birkhoff函数B中被分离出来，即

则aj称为广义Birkhoff系统（1）的分离变量。由方程（1），关于aj的广义Birkhoff方程为

因此，有

于是有如下命题：

命题1对于广义Birkhoff系统（1），设aj为系统的分离变量，如果满足条件

则系统有第一积分

积分（6）可称为广义Birkhoff系统（1）的局部能量积分。

例1 四阶广义Birkhoff系统为[6]

试研究其局部能量积分。

广义 Birkhoff方程（1）给出

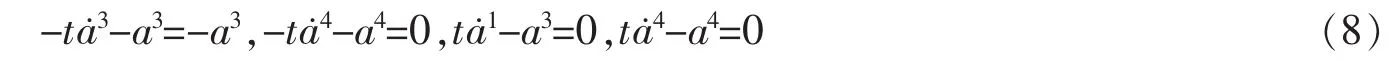
将Birkhoff函数表示为

利用方程（8），易验证

因此，a3是分离变量，而局部能量积分

如果系统有m个独立的分离变量，则对每一个分离变量应用命题1，因此，系统存在m个独立的局部能量积分。

例2 四阶广义Birkhoff系统为

广义 Birkhoff方程（1）给出

将Birkhoff函数表示为

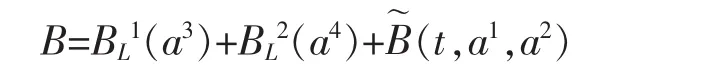
易验证

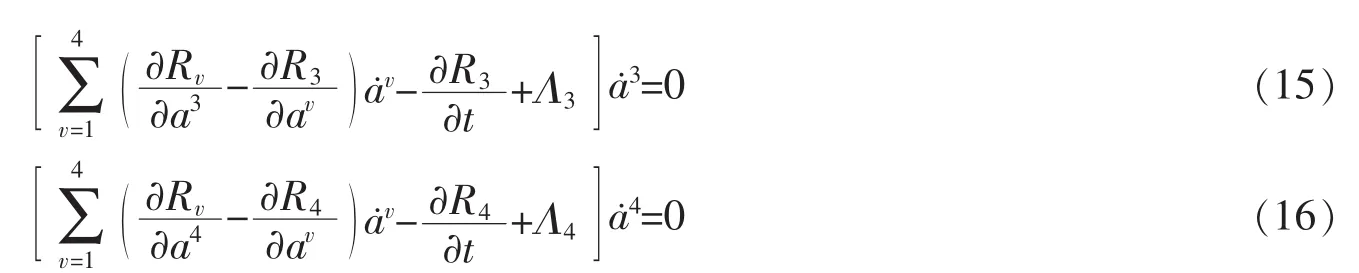
因此，a3和a4是独立的分离变量。应用命题1，得到

式（17）和（18）是相应于分离变量a3和a4的独立的局部能量积分。

2 分离变量为耦合的两个变量时系统的局部能量积分

如果有两个Birkhoff变量，例如aj和ak，可在Birkhoff函数B中被分离出来，即

这里 BL（aj，ak）不能表示为 BL1（aj）和 BL2（ak）之和，则 aj和 ak称为广义 Birkhoff系统（1）的两个耦合的分离变量。由方程（1），关于aj和ak的广义Birkhoff方程分别为

因此，有

于是有如下命题：

命题2对于广义Birkhoff系统（1），设aj和ak是该系统的两个耦合的分离变量，如果满足条件

则系统有第一积分

积分（24）可称为广义Birkhoff系统（1）的局部能量积分。

例3研究Hojman-Urrutia问题，其方程为[17]

令 a1＝x，a2=y，a3=x˙，a4=y˙，方程（25）可化为广义 Birkhoff系统，其中

广义 Birkhoff方程（1）给出

将Birkhoff函数表示为

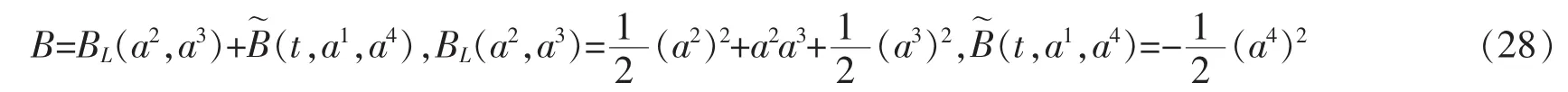
利用方程（27），易验证

因此，a2和a3是该系统的两个耦合的分离变量。根据命题2，得到

式（30）是与分离变量a2和a3相应的局部能量积分。

如果系统有m对耦合的分离变量，则对每一对分离变量应用命题2，因此，系统存在m个独立的局部能量积分。此外，上述方法可进一步拓展到分离变量是由l个变量耦合的情形（l＜2n）。

3 Birkhoff系统的分离变量与局部能量积分

对于Birkhoff系统，其方程为

于是有

命题3对于广义Birkhoff系统（31），设aj为系统的分离变量，如果满足条件

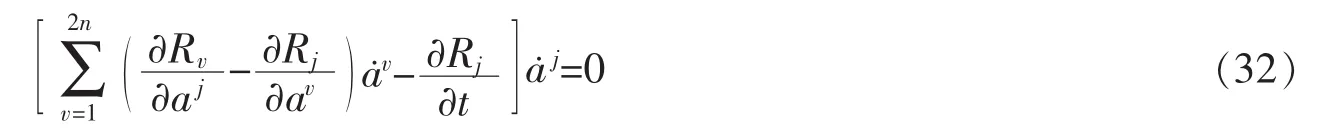
则系统存在局部能量积分

命题3是命题1的推论。

命题4对于广义Birkhoff系统（31），设aj和ak是该系统的两个耦合的分离变量，如果满足条件

则系统存在局部能量积分

命题4是命题2的推论。

例4研究一类动力学系统[1]，其动能为

势能为

其中 v1，v2，…，vn，w1，w2，…，wn是其相应变量的任意函数。

引进广义动量

令

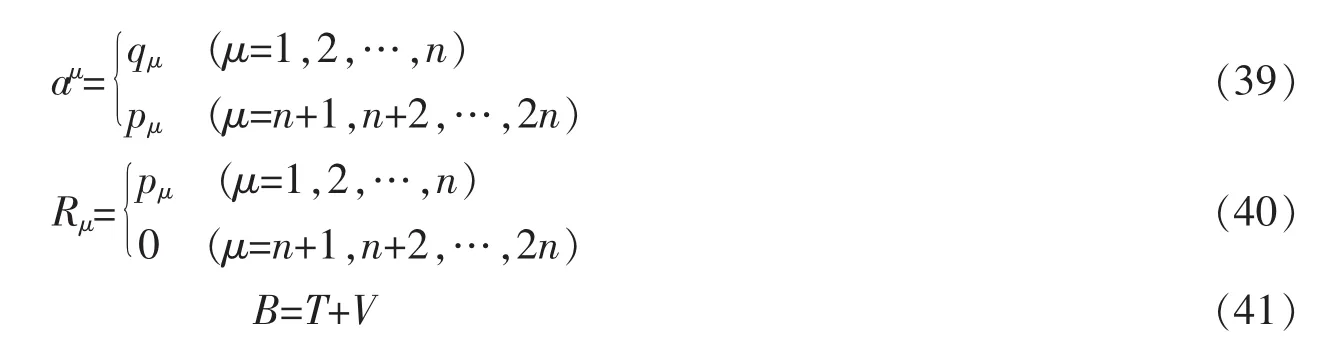
于是有

其中

由于

因此，对每一个s，as和an+s是该系统的两个耦合的分离变量，由命题4，得到

式（45）是系统相应于耦合分离变量as和an+s的局部能量积分。

4 结语

研究动力学系统的积分是分析力学研究的一个重要方面。文章研究了广义Birkhoff系统的分离变量与局部能量积分，给出了局部能量积分存在的条件及其形式，将局部能量积分理论推广到广义Birkhoff系统。文章的主要结果是其中的4个命题。命题1和命题2是一般广义Birkhoff系统的，命题3和命题4是Birkhoff系统的。文章讨论了分离变量为单变量和两个耦合变量情形，这一思路同样适用于多个变量耦合的情形。由于广义Birkhoff系统的一般性，文章给出的方法和结果可进一步推广和应用。

[1]WHITTAKER E T.A Treatise on the Analytical Dynamics of Particles&Rigid Bodies[M].4th ed.Cambridge：Cambridge University Press，2016.

[2]梅凤翔，刘桂林.分析力学基础[M].西安：西安交通大学出版社，1987.

[3]梅凤翔.分析力学[M].上卷.北京：北京理工大学出版社，2013.

[4]梅凤翔.非完整动力学研究[M].北京：北京工业学院出版社，1987.

[5]郑世旺，贾利群.Birkhoff系统的局部能量积分[J].物理学报，2006，55（11）：5590-5593.

[6]梅凤翔.广义Birkhoff系统动力学[M].北京：科学出版社出版，2013.

[7]梅凤翔，张永发，何光，等.广义Birkhoff系统动力学的基本框架[J].北京理工大学学报，2007，27（12）：1035-1038.

[8]张毅.广义 Birkhoff系统的 Birkhoff对称性与守恒量[J].物理学报，2009，58（11）：7436-7439.

[9]ZHANG Yi.The method of variation on parameters for integration of a generalized Birkhoffian system[J].Acta Mechanica Sinica，2011，27（6）：1059-1064.

[10]张毅.广义 Birkhoff系统的 Bertrand 定理[J].苏州科技学院学报（自然科学版），2012，29（4）：1-3.

[11]MEI Fengxiang，WU Huibin.Bifurcation for the generalized Birkhoffian system[J].Chinese Physics B，2015，24（5）：054501.

[12]梅凤翔，吴惠彬.广义Birkhoff系统与一类组合梯度系统[J].物理学报，2015，64（18）：184501.

[13]李彦敏，陈向炜，吴惠彬，等.广义Birkhoff系统的两类广义梯度表示[J].物理学报，2016，65（8）：080201.

[14]葛伟宽，张毅，楼智美.一类广义Birkhoff系统的无限小正则变换与积分[J].物理学报，2012，61（14）：40204.

[15]ZHANG Yi.Stability of motion for generalized Birkhoffian systems[J].Journal of China Ordnance，2010，6（3）：161-165.

[16]SONG Chuanjing，ZHANG Yi.Conserved quantities and adiabatic invariants for fractional generalized Birkhoffian systems[J].International Journal of Non-Linear Mechanics，2017，90：32-38.

[17]SANTILLI R M.Foundations of Theoretical Mechanics[M].New York：Springer，1983.