一类轻量化线性MDS变换的设计与分析*

董新锋，董新科，胡建勇

0 引 言

扩散部件的设计是密码算法设计的重要组成部分。目前，扩散部件主要有MDS矩阵、基于循环移位和异或运算的线性MDS变换、比特置换和二元矩阵等。扩散部件设计的好坏直接影响密码算法的安全性和效率[1-3]。采用差分分支数和线性分支数较大的扩散部件，可以使密码算法更好地抵抗差分攻击和线性攻击。采用结构简单的扩散部件，有利于密码算法的快速实现。线性MDS变换的差分分支数和线性分支数相等且达到最大[4]，故利用线性MDS变换设计分组密码的扩散部件是一种常用的方法。线性MDS变换作为扩散部件被广泛应用于密码算法设计中，如AES算法、Twofish算法、SMS4算法、AIRA算法、HIEROCRYPT算法等。为了保证密码算法的快速有效实现，线性MDS变换对应的MDS矩阵应具有较少的元素和较小的数值。例如，AES算法使用有限域GF(28)上的MDS矩阵为循环移位矩阵；Twofish算法使用GF(28)上的MDS矩阵为Hadamard矩阵；AIRA算法使用GF(2)上的0/1矩阵为对合矩阵，等等。如何设计有限域GF(2n)上快速实现MDS矩阵，一直是人们关心的重要问题，具有较好的理论基础和丰富的研究成果。例如，文献[5-7]等提出可以基于循环移位矩阵、Cauchy矩阵以及Hadamard矩阵等特殊矩阵来设计MDS矩阵的思想和构造方法，并搜索出大量便于实现的MDS矩阵。但是，由于有限域GF(2n)上的乘法运算较为复杂，导致有限域上的MDS矩阵无法满足移动互联网、物联网中诸多资源受限应用场景下的密码算法扩散部件的设计要求。此外，文献[8-14]研究了通常情形下MDS矩阵的构造方法，文献[15-19]研究了轻量级MDS变换的构造方法。

本文将基于循环移位和异或运算，提出一种新的轻量化的线性MDS变换的构造方法，给出该类线性MDS变换的计数结果和相应实例，能够为算法设计提供大量轻量化的线性MDS变换。通过与公开算法中扩散部件的比较分析，说明本文提出的最简形式线性MDS变换具有时延低、运算快、计算资源小等轻量化特性，可以满足移动互联网、物联网中诸多资源受限应用场景下的扩散部件的设计要求。

1 准备知识

本文用⊕表示逐位模2加，用+表示实数加或实数模2m加。对于y=(y1, y2,…, ym)∈GF(2n)m，本文均用W(y)表示y=(y1, y2,…, ym)中非0元的个数。

对于GF(2n)上m×m矩阵A定义的线性变换f(x)=Ax，其差分分支数达到最大值m+1等价于其线性分支数达到最大值m+1。当它的差分分支数达到最大值时，则称A为MDS矩阵。

下面介绍线性变换的差分分支数Bd和线性分支数Bl的定义。

定义1：设f(x)=Ax，且A是GF(2n)上的m×m矩阵，则：

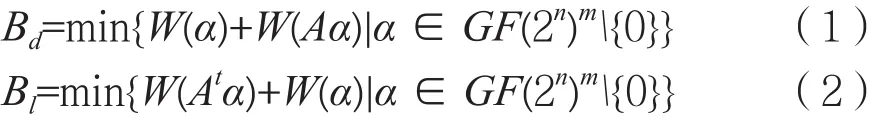
其中矩阵At为矩阵A的转置矩阵。此处用+表示实数加。

定义 2：设A=(aij)2m×2m是GF(2n)上的 2m×2m矩阵，如果当0≤i, j≤2m-1时，均有aij=a0(i+j)，则称A为有限域上的一个循环（Cyclic）移位矩阵，简记为A=Cyc(a00,a01,…,a0(2m-1))。此处，用+表示实数模2m加。

2 基于循环移位和异或运算的线性MDS变换

基于循环移位、异或等简单逻辑运算设计的线性MDS变换，具有结构简单、运算快速、计算资源消耗低等轻量化特征，特别适用于移动互联网、物联网等应用场景下的轻量级密码算法设计。通常情形下，衡量一个密码算法部件的资源占用情况，可以通过基本运算数目的多少来大致刻画。本文的主要目标是寻找具有最少异或数、最少循环移位数和最优分支数等轻量化特征的最简形式MDS变换的设计方法。

目前，主流的密码算法设计中采用的MDS变换扩散部件主要有两类：一类是有限域GF(2n)上分支数为5的4阶或8阶矩阵变换（一般地，n=4、8、16、32等）；另一类是GF(2)上分支数为4、5或8的0/1矩阵变换（对应的矩阵阶数分别为4阶、8阶或16阶）。考虑到密码部件在算法设计等实际应用中的普适性，以下章节均以GF(2)16→GF(2)16的线性MDS变换为例来阐述相关结果，但本文的构造方法及思路适用于设计任意的GF(2n)m→GF(2n)m上的线性MDS变换。

2.1 最简形式1与构造方法1

由线性MDS码的相关结论易知，GF(2)16→GF(2)16的线性变换其比特分支数最优为8。因此，若要使基于循环移位和异或等逻辑运算构造的线性变换L(X)：GF(2)16→GF(2)16为比特分支数为8的MDS变换，则L(X)的表达式中应至少包含7个单项式（即包含6个循环移位和6个异或运算）。此外，考虑到L(X)与L(X＜＜＜i)具有相同的分支数，则对L(X)变换整体做循环移位不会影响其MDS变换的性质，称L(X)与L(X＜＜＜i)为两个等价线性MDS变换。

定义具有如下形式的L(X)为GF(2)16→GF(2)16的基于循环移位和异或等逻辑运算构造的线性MDS变换的最简形式1。

设L(X)是GF(2)16→GF(2)16的线性变换，如果L(X)具有如下形式：

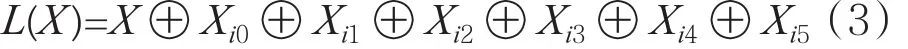
其中Xij(X＜＜＜ij)，且L(X)为MDS变换（即L(X)的分支数达到8），则称L(X)为GF(2)16→GF(2)16具有最简形式1的线性MDS变换。

具有最简形式1的L(X)包含6个循环移位和6个异或运算。其中，6个循环移位运算可以并行计算，具有时延低、运算快、计算资源小等特性，满足诸多轻量化密码算法扩散部件的设计需求。

构造方法1：设L(X)是GF(2)16→GF(2)16的线性变换，且具有如下形式（其中i0、i2、…、i5均为1～15之间互不相同的非零整数）：

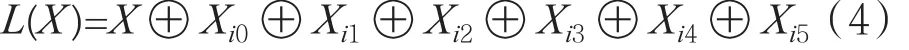
其中 Xij(X＜＜＜ij)。

X通过遍历GF(2)16的216-1个16比特值（全0除外），i0、i2、…、i5（互不相同）通过分别遍历1～15的15个整数值，计算min{W(X)+W(L(X))|X∈GF(2)16{0}}并判断取值是否等于8，即可得到GF(2)16→GF(2)16的所有具有最简形式1的线性MDS变换。

若采用构造方法1，需要遍历的搜索量为(216-，约为228.3。其中为15选6的组合数。

性质1：设L(X)是通过构造方法1得到的GF(2)16→GF(2)16的线性MDS变换，形如式（4），定义Ln(X)为GF(2n)16→GF(2n)16的线性变换，且具有下面的形式：

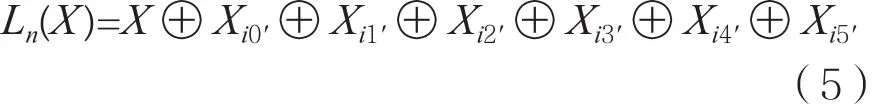
其中Ln(X)。

那么Ln(X)为GF(2n)16→GF(2n)16的线性MDS变换，即验证Ln(X)的等价形式Ln(X)=M·X，其中M为16阶0/1矩阵，M的分支数达到最大值8。

2.2 最简形式2与构造方法2

在密码算法的某些资源受限应用场景下，可以考虑牺牲扩散部件运算的并行性，使得扩散部件占用的资源最少。这种情形下需要通过级联迭代等形式设计扩散部件。下面的构造方法2给出了一种适用于这种资源受限应用场景的GF(2)16→GF(2)16的线性MDS变换设计方法，仅包含4个循环移位和4个异或运算。

设L'(X)是GF(2)16→GF(2)16的线性变换，如果L'(X)具有如下形式：

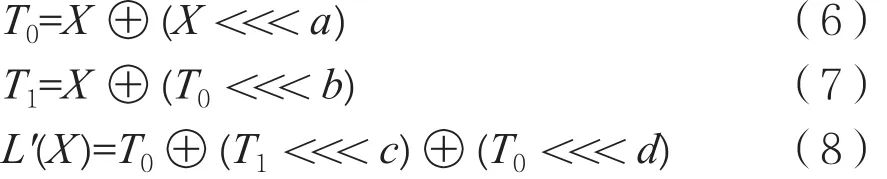
且L'(X)为MDS变换，即L'(X)的分支数达到8，则称L'(X)为GF(2)16→GF(2)16具有最简形式2的MDS变换。

具有最简形式2的L'(X)仅包含4个循环移位和4个异或运算，相对最简形式1具有更低的时延和更小的计算资源占用，但4个循环移位和4个异或运算只能依次串行计算。

构造方法2：设L'(X)是GF(2)16→GF(2)16上的线性变换，且通过如下形式得到（其中a、c、d均为1～15之间互不相同的非零整数，b为1～15之间的非零整数）：

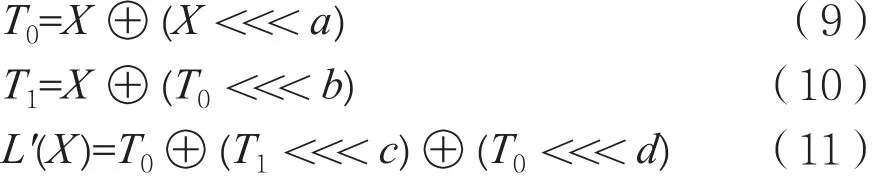
X通过遍历GF(2)16的216-1个16比特值（全0除外），a、c、d（互不相同）通过分别遍历1～15的15个整数值，b通过遍历1～15的15个整数值，计算min{W(X)+W(L'(X))|X∈GF(2)16{0}}，并判断取值是否等于8，即可获得GF(2)16→GF(2)16上的所有具有最简形式2的MDS变换。

若采用构造方法2，需要遍历的搜索量为(216-1)××15，约为 228.8。其中为 15选 3的组合数。性质2：设L'(X)是通过构造方法2得到的GF(2)16→GF(2)16的线性MDS变换，形如式（9）、式（10）、式（11），定义Ln'(X)为GF(2n)16→GF(2n)16上的线性变换，且具有下面的形式：

那么Ln'(X)为GF(2n)16→GF(2n)16的线性MDS变换，即验证Ln'(X)的等价形式为Ln'(X)=M·X，其中M为16阶0/1矩阵，M的分支数达到最大值8。

2.3 最简形式1与最简形式2之间的关系

对最简形式2中的L'(X)展开、化简、合并后，得到如下形式（注：此处“+”为模16加）：

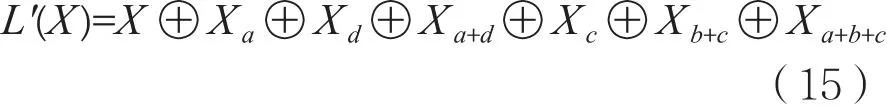
其中 Xi＜＜＜i。

说明最简形式2得到的MDS变换也具有最简形式1的形式，即通过最简形式2得到的MDS变换为通过最简形式1得到的MDS变换的子集。

在有些特殊场景下，可能会对密码算法的扩散部件MDS变换提出更多要求，如要求GF(2n)16→GF(2n)16上的线性MDS变换同时满足上述的最简形式1或最简形式2，此外还满足为GF(24n)4→GF(24n)4上的线性MDS变换，即要求L''(X)满足以下三点：

（1）作为GF(2n)16→GF(2n)16的线性变换，同时满足最简形式1或最简形式2；

（2）作为GF(2n)16→GF(2n)16的线性变换，其分支数达到最优为8，即为MDS变换；

（3）作为GF(24n)4→GF(24n)4的线性变换，其分支数达到最优为5，即为MDS变换。

将满足上述三点性质的L''(X)称为具有特殊形式的MDS变换。

在本文的第3部分，将说明满足上述最简形式的线性MDS变换L(X)、L'(X)、L''(X)的存在性、计数结果等。

3 实例与分析

根据第2部分的构造方法1、构造方法2，通过编程计算，可以得到具有最简形式1、最简形式2和特殊形式的轻量化线性MDS变换的计数结果，如表1所示，并给出了1个构造实例。

表1 轻量化线性MDS变换的计数结果

构造实例1：

通过构造方法1可以得到如下的L(X)：

通过构造方法2可以得到如下的L'(X)：

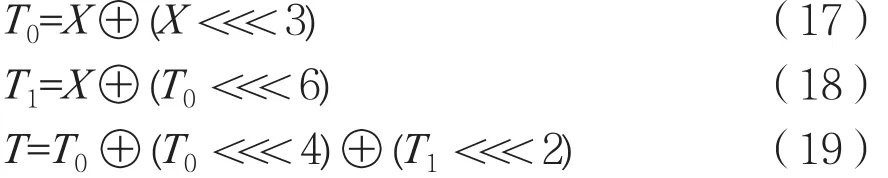
更进一步，通过测试发现L(X)满足以下性质：

（1）作为GF(2)16→GF(2)16的线性变换，其分支数为8，达到最优，即为MDS变换L''(X)；

（2）作为GF(24n)4→GF(24n)4的线性变换，其分支数为5，达到最优，即为MDS变换L''(X)；

表明L(X)同时满足最简形式1和特殊形式，在实际密码算法设计中具有非常明显的实现优势。通过计算机搜索没有发现同时满足最简形式2和特殊形式的L'(X)。

线性MDS变换L(X)对应的0/1矩阵M为：

AIRA算法和HIEROCRYPT算法均为128 bit分组长度的分组密码算法，分别使用了1个16阶0/1矩阵M0和M1，分支数均达到最优为8。

AIRA算法中使用的16阶0/1矩阵M0为：

HIEROCRYPT算法中使用的16阶0/1矩阵M1为式（22）。

通过分析比较容易发现：M与M1相比具有更少的1（M中含有112个1，M1中含有176个1），即M所包含的比特异或数更少，消耗的计算资源更少；M与M0相比具有相同数量的1（均含有112个1），即M与M0包含的比特异或数相同，但由于M是循环矩阵，所以在实现上具有更多的优势和灵活性。

综上所述，本文设计的这类具有最简形式的MDS变换，具有更优良的密码性能和更灵活的实现方式，在诸多资源受限应用场景下的密码算法扩散部件设计中具有极大优势。事实上，还存在其他最简形式的MDS变换，研究方法类似。

4 结 语

本文研究了线性MDS变换的构造方法，在此基础上构造了一类新的轻量化的循环移位线性MDS变换，并给出了该类MDS变换的计数和构造实例。本文的研究结果为循环移位MDS变换的构造方法提供了一种新的途径，丰富了密码算法扩散部件的选择，对密码算法的设计具有实际的应用价值。值得一提的是，这类线性MDS变换构造方法简单，能够快速有效实现。

[1] Schneier B,Kelsey J,Whiting D,et al.Twofish:A 128-bit Block Cipher[EB/OL].(2007-02-02)[2017-11-22].http://www.schneier.com/.

[2] WANG Mei-qin.Differential Cryptanalysis of Present[EB/OL].(2008-01-09)[2017-11-22].https://eprint.iacr.org/2007/408.

[3] WU Wen-ling,ZHANG Wen-tao,FENG Deng-guo.Impossible Differential Cryptanalysis of Reduce Round ARIA and Camellia[J].Journal of Computer Science and Technology,2007,22(03):449-456.

[4] KANG Ju-sung,Hong S,Lee S,et al.Practical and Provable Security Against Differential and Linear Cryptanalysis for Substitution-permutation Networks[J].ETRI Journal,2001,23(04):158-167.

[5] Xiao L,Heys H.Hardware Design and Analysis of Block Cipher Components[C].Proceedings of the 5th International Conference on Information Security and Cryptology-ICISC’02,2003 LNCS 2587:164-181.

[6] Youssef A,Mister S,Tavares S.On the Design of Linear Transformations for Substitution Permutation Encryption Networks[C].Workshop on Selected Areas in Cryptography-SAC’97,1997:40-48.

[7] Blomer J,Kalfane M,Karpinski M,et al.An Xor-based Erasure-resilient Coding Scheme[EB/OL].(1999-10-12)[2017-11-22].https://www.researchgate.net/publication/2643899.

[8] 崔霆,金晨辉.对合Cauchy-Hadamard型MDS矩阵的构造[J].电子与信息学报,2010,32(02):500-503.CUI Ting,JIN Chen-hui.Construction of Cauchy Cauchy-Hadamard MDS Matrix[J].Journal of Electronics &Information Technology,2010,32(02):500-503.

[9] Malik M Y,No J S.Dynamic MDS Matrices for Substantial Cryptographic Strength[EB/OL].(2011-04-05)[2017-11-22].http://eprint.iacr.org/2011/177.

[10]Gupta K C,Ray I G.On Constructions of MDS Matrices from Companion Matrices for Lightweight Cryptography[EB/OL].(2013-02-04)[2017-11-22].http://eprint.iacr.org/2013/056.

[11] Dehnavi S M,Mahmoodi A,Mirzaee M R,et al.Construction of New Families of MDS Diffusion Layers[EB/OL].(2014-12-09)[2017-11-22].http://eprint.iacr.org/2014/011.

[12] Souvik K,Debdeep M.Lightweight Diffusion Layer from the k^th root of the MDS Matrix[EB/OL].(2014-06-22)[2017-11-22].http://eprint.iacr.org/2014/498.

[13] Siang M S,Khoongming K.Lightweight MDS Involution Matrices[EB/OL].(2015-05-19)[2017-11-22].http://eprint.iacr.org/2015/258.

[14] ZHAO Ruo-xin,ZHANG Rui,LI Yong-qiang,et al.On Constructions of a Sort of MDS Block Diffusion Matrices for Block Ciphers and Hash Functions[EB/OL].(2015-05-11)[2017-11-22].http://eprint.iacr.org/2015/449.

[15] Sumanta S,Siang M S.A Deeper Understanding of the XOR Count Distribution in the Context of Lightweight Cryptography[EB/OL].(2016-04-29)[2017-11-22].http://eprint.iacr.org/2016/422.

[16] Sumanta S,Habeeb S.Lightweight Diffusion Layer Importance of Toeplitz Matrices[EB/OL].(2016-09-30)[2017-11-22].http://eprint.iacr.org/2016/835.

[17] Sumanta S,Habeeb S.Analysis of Toeplitz MDS Matrices[EB/OL].(2017-04-23)[2017-11-22].http://eprint.iacr.org/2017/368.

[18] Sumanta S,Habeeb S.Bounds on the Differential Branch Number of Permutations[EB/OL].(2017-10-08)[2017-11-22].http://eprint.iacr.org/2017/990.

[19] Sumanta S,Habeeb S,Rajat S,et al.Lightweight Design Choices for LED-like Block Ciphers[EB/OL].(2017-10-18)[2017-11-22].http://eprint.iacr.org/2017/1031.