一种逐层变化的阈值和改进的小波阈值去噪算法*
周昌顺,张 欣,文 章,张平康
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
0 引 言
随着数字技术的发展,人类生活与活动中的大多数重要角色被数字图像所占据,如卫星电视、X射线透视、天文观测、地理信息系统的开发等都要用到数字图像[1]。然而,图像数据常会受到噪声污染。为了便于图像后期的研究和应用,经常要先对图像进行去噪处理[2]。小波变换作为典型的时-频分析方法,在图像压缩与去噪等研究方向得到了广泛应用。几种小波去噪算法中,小波阈值去噪算法的研究最全面[3]。硬、软阈值函数方法在小波去噪算法中最典型,但硬阈值函数在阈值处不连续,使得重构图像产生了局部振铃现象;而软阈值函数虽无间断点,但有恒定偏差缺陷,导致重构后图像产生了伪吉布斯现像。针对以上不足,文献[4-5]提出了几种改进算法,相对于软、硬阈值去噪结果有了一定改善。本文在参考文献[4-5]方法的基础上,设计了一种改进阈值函数算法。经由改进后阈值函数处理的系数,在阈值处连续,且接近原系数。
1 小波阈值去噪
1994年,Stanford大学的Donoho与Johnstone在高斯噪声模型下,针对多维独立正态变量决策理论,提出了小波阈值去噪算法[6]。随后,他们于1995年提出了硬阈值和软阈值去噪算法,并推导出VisuShrink阈值公式,又称通用阈值法与SureShrink阈值公式,同时证明了其在均方意义下是渐进最优的[7]。由于小波具有低熵性、多分辨性、去相关性和选基灵活性等特点,所以被成功应用于图像去噪。
1.1 小波阈值去噪原理及步骤
1.1.1 基本原理
小波阈值去噪是因为信号x(k)和噪声n(k)转换到小波域中系数具有不同分布特性。有用信号x(k)的能量集中在少数幅度值较大的系数上,而噪声信号n(k)变换后的能量均匀分布在整个高频部分,且系数幅度值较小。随着分解层数N的增加,信号x(k)的小波系数幅度变化较小,而噪声信号n(k)的小波系数快速减小。于是,可以确定合适的阈值T,对分解所得小波系数进行阈值处理。若系数幅度值小于阈值T,认为它是噪号n(k)的系数,把它滤除掉;若系数幅度值大于阈值T,认为它是有用信号x(k)的系数,予以保留。以此原理实现对图像的去噪[8]。
1.1.2 实现步骤
定义含噪图像的基本模型为:

其中f(i, j)是含噪信号,x(i, j)是原始信号,n(i, j)是加性白噪声。含噪图像去噪过程的流程图,如图1表示。

图1 阈值去噪流程
wi,j是噪声图像f(i, j)的小波系数;,ˆijw是去噪函数处理所得的小波系数;为去噪后的重构图像。
1.2 小波阈值的选择
阈值作为小波阈值去噪的关键,如何选择显得尤为重要。迄今为止,众多学者在这方面做了大量研究,其中最著名的是Donoho等人提出的通用阈值(Universal Threshold)[8]:

式中:σn是高斯白噪声的标准偏差;N为小波系数的总和。
Universal Threshold的目标是要消除所有小波系数中幅度值小于噪声小波系数最大幅度值的小波系数。除了Universal Threshold外,还有Donoho和Johnstone在1995年提出的SURE阈值[9],主要是在每一分解层采用不同阈值,目标是使原图像与去噪图像间均方差最小。
SURE阈值如下:

其中:t为初始阈值,wj表示来自子带j的小波系数。
Bayes Shrink阈值,前提是假定小波系数服从广义的高斯分布,应用Bayse数学框架,以最小Bayes平均风险为准则,获得各子带的小波系数为:

此外,还有Chang等人提出的局部自适应阈值[10],Nason等提出的基于Cross-Validation准则的阈值[11]等。
1.3 常见的小波阈值函数
1.3.1 硬阈值函数(Hard Threshold)
硬阈值函数去噪原理是把噪声图像分解所得小波系数与给定阈值相比较。若系数幅值的绝对值大于给定阈值,则保留系数;相反,则把系数置零。硬阈值函数的表达式如下:

其中wi,j为含噪图像小波系数,T为给定的阈值,H(,ˆijw)为经硬阈值函数处理所得的小波系数。
1.3.2 软阈值函数(Soft Threshold)
软阈值函数法与硬阈值法类似,也是将绝对值小于给定阈值的系数置零;相反,则将小波系数减去阈值再予以保留。软阈值函数的表达式如下:
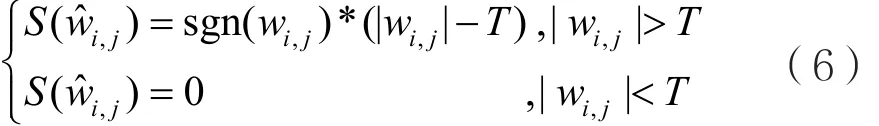
其中wi,j是含噪图像小波系数,T是给定的阈值,S(,ˆijw)是经软阈值函数处理所得的小波系数sgn(·)是符号函数。
从以上两种典型去噪算法不难看出,对于硬阈值函数,在阈值处间断,使得去噪重构图像产生局部振铃现象;对于软阈值函数,存在一个偏差T,导致去噪重构图像产生伪吉布斯现像,导致图像模糊失真,降低了视觉效果。
2 改进阈值函数及变化阈值
2.1 逐层变化的阈值
鉴于噪声与图像分解系数在小波域分布特性的不同,采用通用阈值会产生“过扼杀”的缺陷,使得随着分解层数增加图像有用信息丢失严重。对于以上缺点,要求设计阈值时根据图像和噪声小波系数的特点,随着各分解层系数的变化自适应地改变。本文在参考文献[4,12]方法的基础上,给出了一种逐层变化阈值:

其中j为分解层数,Tj对应第j层阈值,M、N分别是第j层高频系数的行和列,σj是噪声的标准差。Donoho等提出了一种利用噪声图像的小波变换系数估计噪声方差的方法为[13]:
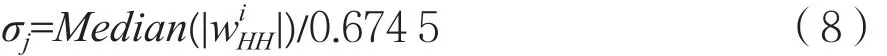
该方法的原理主要基于以下两点:
(1)经由小波分解所得各层高频系数中,第一层高频系数子带HH主要是噪声小波系数;
(2)假定{un}由N个相互独立、零均值、方差为的高斯随机变量组成,则有:
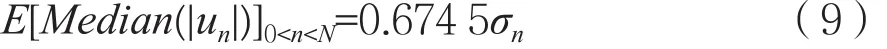
2.2 改进连续可导阈值函数
本文针对软、硬阈值函数的固有缺点以及参考文献[4-5]所用方法,提出了一种改良阈值函数:

考察分段函数:
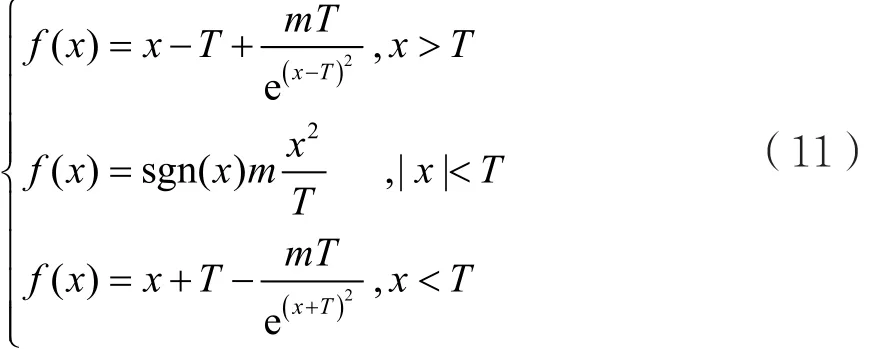
当 x→ T+时,f(x)→ mT; 当 x→ T-时,f(x)→mT;当x→-T-时,f(x)→-mT,当x→-T+时,f(x)→-mT。所以,f(x)在阈值间断点T+-处连续,这就克服了硬阈值函数的间断问题。当|x|→∞时,表明函数f(x)以y=x为渐近线,完善了软阈值函数存在恒定偏差的问题。此外,当|x|>T时,f(x)高阶可导,便于数学上的后续分析。式(10)中的m>0,当m=0时,是软阈值函数的表达式,同时在|wi,j|<T这个区域是将小波系数按照一定的比例缓慢收缩减小而不是直接置零。这样处理的结果就是使重构图像更加平滑,同时极大改善图像的边缘模糊程度,使主观视觉的效果更好。
3 实验仿真
为了体现本文算法对含噪图像去噪效果的优越性,选取硬阈值、软阈值去噪函数和文献[4-5]方法的去噪效果进行对比。实验环境为Matlab 7.1,初始图像选取大小为512×512的lena、Barbara、Peppers灰度图像。在三幅原始图像中添加零均值,方差为0.005、0.01、0.02的高斯白噪声。因为“sym”类小波具有良好的对称性,所以选用“sym4”小波基对含噪图像进行3层分解,最后以均方误差(MSE)与峰值信噪比(PSNR)作为去噪后图像的客观评价标准来评价各个算法。
这里给出在噪声方差为0.02时的去噪效果图,如图2、图3和图4所示。需要说明的是,本文改进算法在m=0.1时去噪效果最好。

图2 σ2=0.02时lena图像去噪效果对比

图3 σ2=0.02时的Barbara图像去噪效果对比

图4 σ2=0.02时的Peppers图像去噪效果对比
图 2、 图 3和 图 4给 出 了 lena、Barbara、Peppers图像在方差是0.02的高斯白噪声时主观去噪效果对比。虽然以上各种去噪算法都不能完全将图像中的干扰噪声消除,但可以看出,尤其图3的Barbara图像纹理细节较为丰富,图像的去噪效果更直观;本文改进算法对Barbara的细节部分保留更为完整,去噪效果比硬、软阈值和文献[4-5]方法,图片的边缘细节更加清楚,对噪声抑制效果更好。
图2、图3和图4给出了主观视觉评价,而在客观评价中,常以均方误差(MSE,如表1所示)与峰值信噪比(PSNR,如表2所示)为标准来评价去噪后的重构图像质量。均方误差的公式如下:
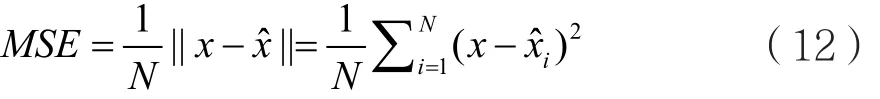
式中:xi为初始图像的第i个像素值,ˆix为去噪后图像的第i个像素值。N为原始图像的像素数。于是,峰值信噪比为:
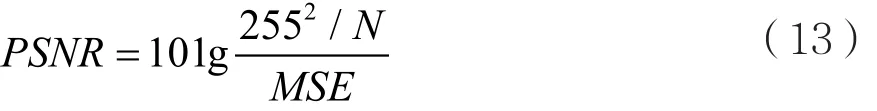
需要说明的是,峰值信噪比(PSNR)常用于二值灰度图像的去噪效果评估。

表1 不同去噪函数去噪后图像的均方误差MSE(单位:×10-3)
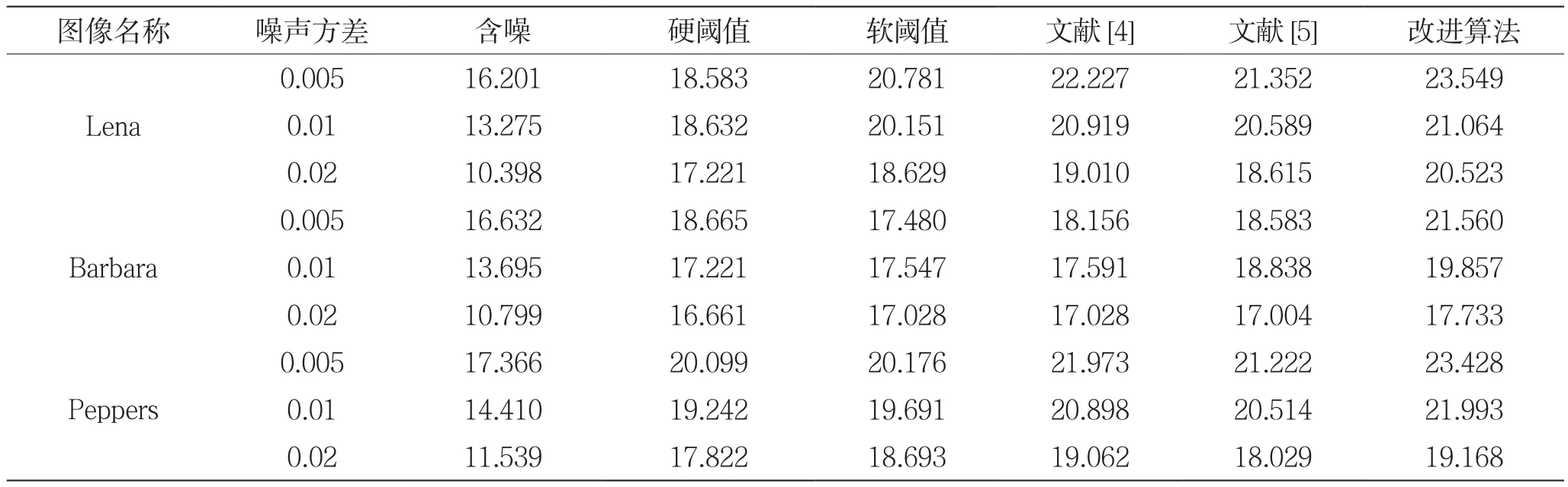
表2 不同去噪算法去噪后图像的峰值信噪比PSNR(单位:dB)
由表2和表3可以得出基于本文改进算法去噪后图像的峰值信噪比相对于硬、软阈值提高了2~3 dB,对比参考文献[4-5]算法去噪后图像峰值信噪比也更高,并且均方误差值也更小,因此本文改进算法的有效性也得到了充分体现。
4 结 语
本文在研究了小波阈值去噪原理以及经典硬、软阈值函数的缺陷,并在借鉴一些学者所取得成果的基础上,提出了一种逐层变化的阈值和改进阈值函数去噪算法。该算法不仅消除了硬、软阈值函数的固有缺点。实验结果表明:同时在重构图像的纹理细节以及边缘信息保留也更为完整,无论是在主观方面的视觉效果还是客观评价图像去噪效果的峰值信噪比(PSNR)和均方误差值(MSE)都有较好的提升和改善。
[1] 张国伟.基于小波变换的图像去噪方法研究[D].昆明:昆明理工大学,2014.ZHANG Guo-wei.Image Denoising Method Based on Wavelet Transform[D].Kunming:Kunming University of Science and Technology,2014.
[2] 姜三平.基于小波变换的图像降噪[M].北京:国防工业出版社,2009:1-4.JIANG San-ping.Image Denoising Method Based on Wavelet Transform[M].Beijing:National Defence Industry Press,2009:1-4.
[3] 王蓓,张根耀,李智等.基于新阈值函数的小波阈值去噪算法[J].计算机应用,2014(05):1499-1502.WANG Bei,ZHANG Gen-yao,LI Zhi,et al.Wavelet Threshold Denoising Algorithm Based on New Threshold Function[J].Computer Application,2014(05):1499-1502.
[4] 李朋,余谅.一种改进的小波阈值去噪方法[J].现代计算机:专业版,2016(07):72-75,83.LI Peng,YU Liang.An Imroved Wavelet Threshold Denoising Method[J].Modern Computer:Professional Edition,2016(07):72-75,83.
[5] 李晓飞.基于小波变换的图像去噪方法研究[D].南京:南京邮电大学,2016.LI Xiao-fei.Research on Image Denoising Method Based on Wavelet Transform[D].Nanjing:Nanjing Unversity of Posts and Telecommunications,2016.
[6] Donoho D L.De-noising by soft-thresholding[J].IEEE Tran.on IT,1995,41(03):612-626.
[7] 张郝.基于小波变换的图像去噪方法研究[D].北京:北京交通大学,2008.ZHANG Hao.Research on Image Denoising Method Based on Wavelet Transform[D].Beijing:Beijing Jiaotong University,2008.
[8] 程正兴,杨守志,冯晓霞.小波分析的理论算法进展和应用[M].北京:国防工业出版社,2007.CHENG Zheng-xing,YANG Shou-zhi,FENG Xiaoxia.The Progress and Application of The Theoretical Algorithm of Wavelet Analysis[M].Beijing:National Defence Industry Press,2007.
[9] Donoho D L,Johnstone I M.Adeal Spatial Adaptation by Wavelet Shrinkage[J].Biometrika,1994,81(03):425-455.
[10] Chang S G,Yu b,Vetterli M.Adaptive Wavelet Thresholding via a Denoising and Compression[J].IEEE Trans. Image Process.,2009,9(09):1532-1546.
[11] Nason G P.Wavelet Regression by Crossvalidation[Z].Technical Report 447,Department of Statistics,Stanford,1994.
[12] 欧晓旭.基于小波阈值的图像去噪研究[D].哈尔滨:哈尔滨理工大学,2016.OU Xiao-xu.Image Denoising Research Based on Wavelet Threshold[D].Harbin:Harbin University of Science and Technology,2016.
[13] Donoho D L,Johnstone I M.Ideal Spatial Adaptption by Wavelet Shrinkage[J].Biometrika,1994,81(03):425-455.

