银行间同业拆借利率的波动性研究
冷琦琪,王学军
(武汉大学经济与管理学院,武汉430072)
0 引言
作为我国货币市场的基准利率,上海银行间同业拆借利率(简称Shibor)影响着市场化定价的金融产品的价格。近几年来,受国内外经济环境变化,尤其是货币政策及资金供求关系变化的影响,金融市场跌宕起伏,几度出现“钱荒”;以上海银行间同业拆借利率为代表的利率市场时常出现异常波动,给商业银行及工商企业带来较大的利率风险。因此,深入研究Shibor的运行规律、波动特征及风险价值,精准计量和管理利率风险,对于维护金融安全和支持经济发展都具有重要的意义。
现有文献多从Shibor作为基准利率的可行性[1-4]和有效性[5]、及Shibor自身的波动性和杠杆效应[6]等角度进行研究。虽然具有重要的参考价值,但是却表现出一定的局限性:一是鲜见学者运用ARFIMA模型对Shibor进行分析,对Shibor的长记忆性缺乏研究;二是尽管运用了EGARCH模型,但只是从几个侧面比较分析Shibor波动的个别特征,对Shibor波动的研究缺乏系统性;三是鲜见学者运用符号偏差验证方法对EGARCH模型进行诊断。鉴于此,本文旨在综合运用ARFIMA和六种不同分布下的EGARCH及VaR模型,从四个方面进行改进:一是运用ARFIMA分析Shibor的长记忆性;二是运用六种不同分布下的EGARCH模型验证Shibor的非对称性等特征;三是运用符号偏差验证方法对六种不同分布下的EGARCH模型进行诊断,判断模型的适用性;四是运用VaR模型进行回验,选出最优的模型。
1 模型选取与数据来源
1.1 模型选取
1.1.1 ARFIMA模型
ARFIMA模型描述的是长期记忆过程,即时间序列过去的某一时刻的冲击会持续影响到未来很长一段时间。
若平稳时间序列{xt},满足差分方程:

1.1.2 GARCH/EGARCH模型
为了改进ARCH模型,Bollerslov(1985)[8]阐述了广义自回归条件异方差(GARCH)模型。对于一个对数收益率序列rt,令at=rt-μt为t时刻的新息。我们称at服从GARCH(m,s)模型,若at满足:

其中,{εt}是均值为0、方差为1的独立同分布随机变量序列,
为了优化GARCH模型,Nelson(1991)提出的EGARCH模型反映了正的和负的资产收益率的非对称效应,纳入加权的新息:

故EGARCH(m,s)模型的条件方差函数为:
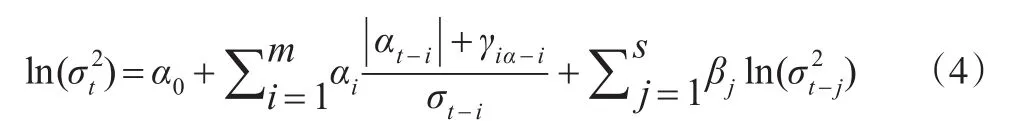
1.1.3 模型诊断
借鉴Engle和Ng(1993)[9]论述的符号偏差验证方法(SBT)、正向符号偏差验证方法(PSBT)及负向符号偏差验证方法(NSBT)和联合验证方法(JT),来诊断7dwshibor不同强度的正(负)收益率的非对称效应能否有效体现在所拟合的EGARCH模型中。
SBT验证的表达式为:

PSBT验证表达式为:

NSBT验证的表达式为:

JT将以上三个验证结合起来,联合进行验证,验证表达式为:
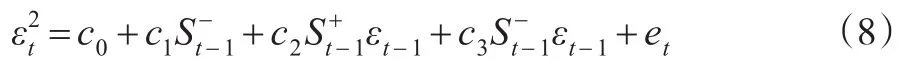
1.1.4 VaR的回验方法——似然比(LR)回验
VaR是指在未来某一特定时期内,在普通市场条件和某一既定的置信水平下,某项金融资产或投资组合预期可能遭受的最大损失。VaR模型的回验是核验其计量结果对实际损失的覆盖程度,以确保其有效性。Kupiec(1995)[10]提出了无条件覆盖POF回验方法,实际回验天数为M,回验中实际例外天数为X,例外的概率估计为p=X/M。假设:H0:p=p*,H1:p≠p*,公式为:

LRpof服从自由度为1的χ2分布。置信区间为95%时的临界值为3.841。若LRpof<3.841,则不能拒绝零假设,即VaR模型很好地拟合样本数据。反之,不能很好地拟合样本数据。
然而Christoffersen(1998)[11]认为,Kupiec回验忽视了VaR例外发生时间的变化,于是提出了对无条件覆盖和例外值的独立性的联合检验,假设H0:某天VaR模型回验例外与前一天是独立的;H1:非独立的。公式为:

LRind服从χ2(1)分布。下标0代表没有例外,1代表例外;n00表示VaR模型回测没有例外且前一天也没有例外,n01表示回测例外但前一天没有例外,n10表示回测没有例外但前一天例外,n11表示回测例外且前一天也例外;π01=n01/(n00+n01),π11=n11/(n10+n11),π2=(n01+n11)/(n00+n01n10+n11)。
以前述公式为基础,Christoffersen(1998)[11]将和结合起来,阐述了时间独立性和覆盖程度的混合回验,如式(11)所示:

服从χ2(2)分布,利用LRcc统计量可同时对时间独立性和覆盖程度进行回验。
1.1.5 sged分布
由于正态分布和t分布不能有效地拟合资产收益分布的“厚尾”和“有偏”特征,从而造成σ或VaR的低估或高估。为了解决这一问题,Theodossiou(2000)[12]提出了具有长尾带偏形状的有偏广义误差分布(简称sged),可以比较精确地分析“有偏”与“厚尾”的特征。Lee等(2008)[13]的研究结论表明,基于sged的GARCH分析可以更为精确地计量VaR。鉴于此,本文运用sged与std等分布对比进行GARCH分析和VaR回验。
假设εt~sged(0,1),概率密度函数为:

sign(·)表示符号函数,ν衡量收益分布尾部的厚薄程度,当ν<2时,sged的尾部比正态分布更厚;当ν=2,ξ=0时,sged转化为标准正态分布;当ν>2时,sged的尾部比正态分布更薄;ξ表示偏度参数,当ξ=0时,sged转化为ged;如果ξ<0,则sged的尾部表现为左偏;如果ξ>0,则sged的尾部表现为右偏。
1.2 数据来源
本文选取7天Shibor(简称7dwshibor)的周数据来反映Shibor的波动情况,所取的样本数据来源于汤姆森路透资讯,范围是2006年10月13日至2017年6月9日,共计546个样本数据。
设rt为7dwshibor序列的对数收益率,记对数序列的一阶差分的收益率序列数学表达式为rt=[log(xt)-log(xt-1)]*100。
2 实证分析
2.1 正态性检验
运用Shapiro-Wilk normality检验方法对rt序列进行正态性检验。得到W=0.8483,小于1,在α=0.05的置信水平下,p值小于2.2e-16,有足够理由拒绝其符合正态分布。
2.2 偏度与峰度分析
通过计算rt序列的均值、标准差、偏度、峰度等统计指标(见表1),可以发现:rt序列的偏度小于0,峰度远大于3,呈现左偏尖峰厚尾的分布形态。这意味着rt序列的分布在尾部比正态分布有更多的异常值,也就意味着有更大的尾部风险。

表1 描述性统计
2.3 ARFIMA模型的建立
R语言中有自动选择ARIMA参数的函数auto.arima(),可以作为有价值的参考。本文运行该函数,结果推荐ARMA(1,1)。为了比较各种模型的效果,本文运行了非自动选择参数的AR(1)、MA(1)、ARMA(1,1)、ARIMA(1,1)、ARIMA(1,1,1)模型,结果如表2所示。

表2 ARFIMA(1,0.4662,1)与ARIMA(1,1,1)等模型比较
ARMA(1,1)在这些模型中的确比较好,误差平方、极大似然函数值、aic值均优于其他模型。但ARIMA没有考虑长记忆性,还需构建ARFIMA模型。
利用R语言中fracdiff程序包中的若干函数,通过极大似然函数等方法求得对d的估计值为0.4662。根据Brockwell和Davis(2009)[7]的判断标准,rt序列符合长记忆特征。同时也求得AR及MA的系数φ1=0.8435,θ1=0.7154,而这三个估计量的标准误差为0.1657753、0.9374268及0.6220559。记忆参数d的估计值在平稳和可逆的区间(0,0.5)内,接近非平稳的边界0.5,系数的标准差高度显著。因此,这些数据更适合于ARFIMA(1,0.4662,1)模型。拟合的模型的数学表达式为:
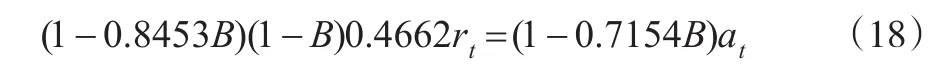
从表2可以看出,ARFIMA(1,0.4662,1)的误差平方、极大似然函数值、aic值均优于AR(1)、MA(1)、ARMA(1,1)、ARIMA(1,1)、ARIMA(1,1,1)。所以,构建ARFIMA(1,0.4662,1)更为合适。
2.4 ARFIMA模型残差的ARCH效应检验
ARFIMA模型的残差是否表现出ARCH效应(条件异方差性)可运用拉格朗日乘子法(Lagrange Multiplier,ARCH-LM)检验。如表3所示,表中显示p值小于0.05,可以拒绝零假设,说明ARCH效应存在于残差序列之中,rt序列的残差表现出条件异方差性。

表3 rt序列残差ARCH-LM检验结果
2.5 ARFIMA-EGARCH模型的建立
由于ARFIMA模型的残差存在ARCH效应,则可以在其基础上建立ARCH模型。由于ARCH模型阶数达到12阶,难以进行适当的拟合;则考虑运用GARCH(1,1)模型。由于rt序列可能存在非对称效应,则运用EGARCH(1,1)模型更好一些。
本文运用R语言中rugarch package对10年7dwshibor周数据进行运算,试图对比正态分布(norm)、偏正态分布(snorm)、学生t分布(std)、偏学生t分布(sstd)、广义误差分布(ged)及偏广义误差分布(sged)六种不同分布下的EGARCH模型,见表4。

表4 六种不同分布下的rt序列残差EGARCH模型
由表4可知:(1)从总体上看,各种模型的对数似然函数值和模型系数都相当显著,拟合效果均比较理想。(2)各种模型中的各项系数均高度统计显著。GARCH系数即β值接近于1,rt序列的波动表现出明显的波动聚集效应,小的波动之后往往伴随着小幅度的波动,平静期往往跟随着平静期;大的波动之后往往伴随着大幅度的波动,振荡期往往跟随着振荡期。(3)参数各种模型中γ均大于0,表现出明显的与股票等金融资产相反的非对称性杠杆效应,称作“反杠杆效应”。(4)参数v体现分布尾部的厚薄程度,ged和sged的v估计值均小于2,说明序列有明显的厚尾特征。(5)参数ξ=-0.0829小于0,说明rt序列呈现出明显的左偏形态。这对VaR的精准计量具有非常重要的作用。(6)无论从AIC、BIC、SIC和HB信息准则来看,还是根据对数似然函数值来判断,拟合效果最好的是sged分布,其次是sstd和ged分布,再次是snorm分布和norm分布,最差的是std分布。所以,使用sged分布对该EGARCH模型进行估计,得到rt序列的估计结果为:
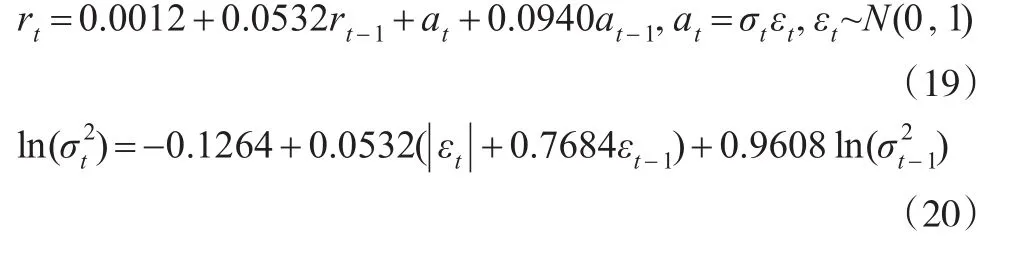
所有参数估计值在5%水平下都是统计显著的。关于模型的检验,对标准残差序列,Ljung-Box统计量为Q(5)=10.277(0.06777)和Q(10)=20.73(0.05305);而对平方序列,Q(5)=2.663(0.7518)和Q(10)=7.1564(0.7106),括号中的数是相应的p值。这些都说明所拟合的模型是充分的。

作反对数变换,有:

由式(22)可看出EGARCH模型下波动率对过去正的和负的“扰动”的不对称反应。例如,当标准化的“扰动”数量为两个标准差时,有:

因此,波动率对变动两个标准差正的“扰动”的反应比相同强度的负“扰动”的反应要大17.77%。这进一步说明EGARCH模型的非对称特征。如果γ>0,显示好消息(即εt-1>0)对rt条件方差的对数产生的冲击效果要大于坏消息;反之,则显示坏消息表现出更强的杠杆效应;因此,γ可以用来评价7dwshibor波动是否符合理性。
从图1可以看出,其在“扰动”大于0的部分波动率的变化比小于0的部分大,也就意味着正“扰动”带来的波动率的变化更大一些。帕森德流动性黑洞理论可以较好地解释7dwshibor对信息反应的非对称性:由于外部经济环境的变化,监管机构的要求及金融机构内部风险控制的需要,在某个时刻,市场流动性骤然消失,拆借利率价格飙涨。在每年6月末、年末、“十一”黄金周之前,单位集中发放绩效工资、居民取款消费骤增,社会资金突然紧张,7wshibor随之突然上升;这些现象证实了这一点。
2.6 模型诊断结果
从表5可以看出,7dwshibor EGARCH模型的六种不同分布下对应的SB、NSB、PSB及Joint统计量均显著不等于0,不同程度的正负向冲击对条件方差的影响效果不同,未预料变动的大小和方向对波动的影响也不同,表明7dwshibor的收益率条件方差具有显著的不对称性。因此,这些模型都是合适的。

图1 7dwshibor序列对信息冲击的反应
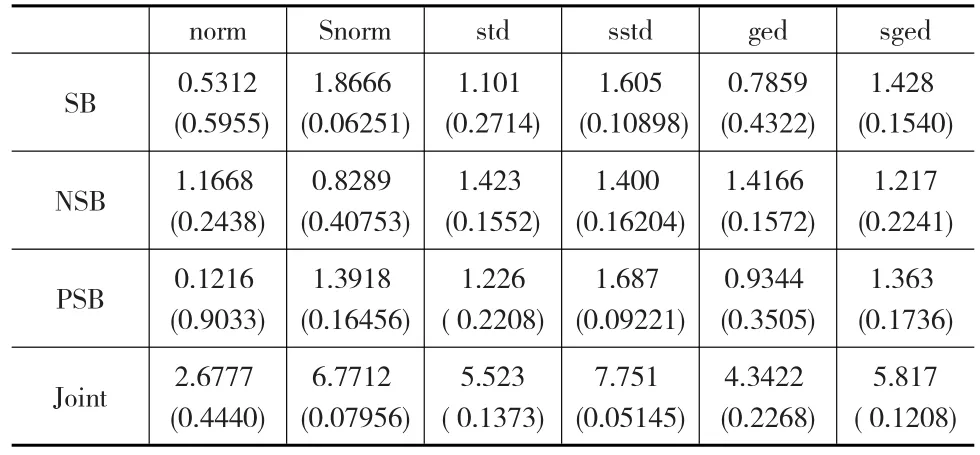
表5 7dwshibor模型的诊断检验结果
2.7 VaR的回验
根据前述各种EGARCH模型的参数估计值,通过R语言RUGARCH包采用95%的置信度计算VaR、例外天数及例外率和LRpof、LRcc统计量,以检验所构模型的有效性。表6为在六种不同分布下以前300个观测值为基础、向前一步滚动计算VaR的Kupiec和Christoffersen统计值,回验244天的结果。
由表6可知,从例外天数看,除sstd分布之外,其他五种不同分布都在Kupiec确定的非拒绝区域内;以例外率排序,EGARCH-sstd>snorm>std>ged>norm>sged,基于sstd分布假设的EGARCH模型拟合的效果最差,例外率超过标准值1.1个百分点,零假设被拒绝;EGARCH-sged模型拟合的效果最好,例外率低于标准值2.5个百分点。从LRpof统计量看,EGARCH-sstd>snorm>std>ged>norm>sged,EGARCH-sstd分布模型拟合的效果最差,超过标准值0.09个百分点,零假设被拒绝;EGARCH-sged模型拟合的效果最好,低于标准值近3.1个百分点。从LRcc统计量看,EGARCH-sstd>snorm>std>ged>norm>sged,EGARCH-sstd分布模型拟合的效果最差,超过标准值0.84个百分点,零假设被拒绝;EGARCH-sged模型拟合的效果最好,低于标准值4.18个百分点。因此,EGARCH-sged分布的回测效果最好,sged分布能比较准确地捕捉rt序列的波动性。
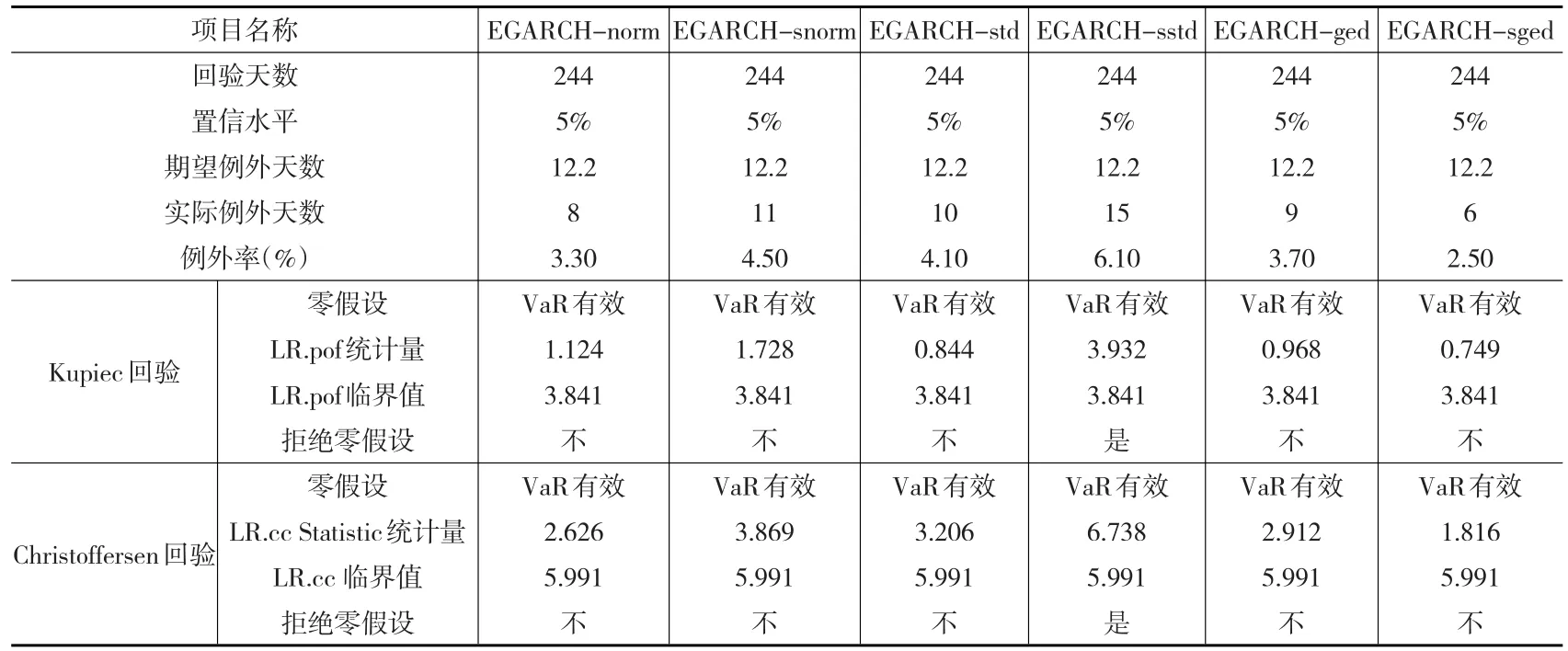
表6 Kupiec和Christoffersen的VaR回验结果
3 结论
本文以上海银行间同业拆借利率(Shibor)为研究对象,选取7dwshibor为代表,以ARFIMA和EGARCH模型作为研究工具,对其表现的长记忆性、波动聚集性及非对称性等特征进行研究。结果表明:
(1)由于存在市场经济体制尚不完善、金融市场尚不发达、同业拆借市场的报价机制不成熟、市场信息不对称等问题,7dwshibor在统计上表现出左偏尖峰厚尾的非正态分布特征。
(2)通过ARFIMA模型计算得到记忆参数d=0.4662,GARCH系数即β值接近于1,说明rt序列表现出长记忆性,即序列过去某一时刻的冲击会持续影响到未来很长一段时间。
(3)由于残差序列表现出显著的ARCH效应,运用EGARCH模型拟合发现rt序列表现出明显的波动聚集性、“反杠杆效应”、厚尾性和左偏形态。
(4)符号偏差验证结果显示EGARCH模型拟合rt序列是合适的。
(5)VaR的回验结果显示EGARCH-sged模型能比较准确地拟合rt序列的波动性,可以有效地计量7dwshibor风险。
[1]项卫星,李宏瑾.货币市场基准利率的性质及对Shibor的实证研究[J].经济评论,2014,(1).
[2]王志栋.中国货币市场基准利率选择的实证研究[J].投资研究,2012,(1).
[3]中国人民银行货币政策分析小组中国货币政策报告2007—2015[R].北京:中国人民银行,2016.
[4]戴国海,李伟.Shibor在我国基准利率体系中的地位及其完善渠道研究[J].金融监管研究,2013,(6).
[5]李良松.上海银行间同业拆放利率VaR的有效性研究[J].金融研究,2009,(9).
[6]吴俊,杨继旺.上海银行间同业拆放市场杠杆效应[J].管理现代化,2015,(1).
[7]Brockwell P J,Davis R A.Time Series:Theory and Methods(2nd ed)[M].New York:Springer,2009,.
[8]Bollerslev T.A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return[J].The Review of Economics and Statistics,1987.
[9]Engle R F,Ng V K.Measuring and Testing the Impact of News on Volatility[J].The Journal of Finance,1993,48(5)
[10]Kupiec P H.Techniques for Verifying the Accuracy of Risk Measurement Models[J].The Journal of Derivatives,1995.
[11]Christoffersen P.Evaluating Interval Forecasts[J].International Economic Review,1998,39(4).
[12]Theodossiou P.Skewed Generalized Error Distribution of Financial Assets and Option Pricing[R].Working Paper,Cyprus University of Technology,2000.
[13]Lee M C,Su J B,Liu H C.Value-at-risk in US Stock Indices With Skewed Generalized Error Distribution[J].Applied Financial Economics Letters,2008,(4).

