基于模型误差EKF-HIF算法的锂动力电池SOC联合估计
程明, 娄柯
(安徽工程大学电气工程学院, 安徽芜湖241000)
引言
近年来,由于大量燃油汽车所带来的能源短缺、环境污染和温室效应等问题日益严重,以车载电池为主要动力的电动汽车得到快速发展[1-2]。锂离子电池具有自放电小、循环特性好、可快速充放电、能量效率高等优点,成为了目前电动汽车的主要动力源[3]。电池需要提供整车的全部功率和能量,为了保证电池的安全及使用寿命最大化,对其有效管理至关重要。
电池的荷电状态(State of Charge, SOC)无法直接测量得到,需要建立相应的数学模型和估计算法,通过测量其它物理量间接得到。目前,国内外许多学者对电池SOC的估计进行了深入研究[4]。Santhango-palan和White等人[5-6]提出用扩展Kalman和无痕物理模型滤波器对锂离子电池进行SOC预测。林成涛等人[7]率先引入折算库仑效率思想,同时考虑了温度和电池老化影响因素,采用常规方法组合算法估计电池SOC。雷肖等人[8-9]针对动力电池电能容量判别问题,分别采用支持向量机方法和神经网络方法估计荷电状态,实验表明了SOC估计器的基本性能,比较了两种方法的估计精度。徐颖[10]等人分析了SOC与之相关的主要影响因素之间关系,着重考虑温度对电池内阻的影响,建立了能模拟电池动态性能的二阶RC等效电池模型预测电池的荷电状态。何洪文[11]等人基于混合动力脉冲功率特性试验,为保证观测器收敛和李亚普若夫意义下稳定的条件,引入滑模观测器算法,结果表明该算法具有更好的估计精度和鲁棒性。张洁[12]等人主要以实验测试的电池数据为基础,将粒子滤波算法应用到电池模型中,利用实测数据进行电池SOC的估计实验,并采用遗传粒子滤波算法解决了粒子退化等问题。
以上文献针对电池荷电状态估计策略从不同角度以及不断改进的方法进行了大量的研究分析。研究表明在较强的有色噪声情况下EKF滤波器会发生严重发散,H∞滤波具有较强的鲁棒性能,比Kalman产生更好的滤波效果;而在白噪声情况下EKF算法可以进行最小方差最优估计,比H∞滤波估计效果更为明显[13-14]。为此,本文主要研究噪声引起的误差,利用模糊神经网络算法来预测电池模型误差,采用EKF-HIF联合算法对SOC进行估计,有效消除由于较大模型误差和测量噪声引入的估计误差,从而大大提高SOC的估计精度,并与传统基于EKF的SOC估计方法相比较。
1 电池等效电路模型
1.1 PNGV电池模型
动力电池SOC的估计需要建立精确的且易于实现的电池模型,等效电路模型研究的是电池在工作过程中电压与电流的外部特性,可以用电路中常用的元器件表示电池动态性能。该电路模型构造清晰,元器件的物理意义明确,可以用数学解析式准确地表达模型且模型参数也容易辨识,普遍应用于实际工况中。本文采用《PNGV电池试验手册》中的标准电池性能模型[15],该模型是典型的非线性等效电路模型,如图1所示。图中Uoc为电池处于理想状态下两端电压源,表示电池的开路电压,电容Cb表示外接负载时由于电流累积产生的压降变化,Uoc和Cb串联表示开路电压UOCV的变化;R0表示电池的欧姆内阻;Rp和Cp分别表示电池的极化电阻和极化电容,并联形成的阻容回路可以描述充放电停止后电池端电压的回滞过程。
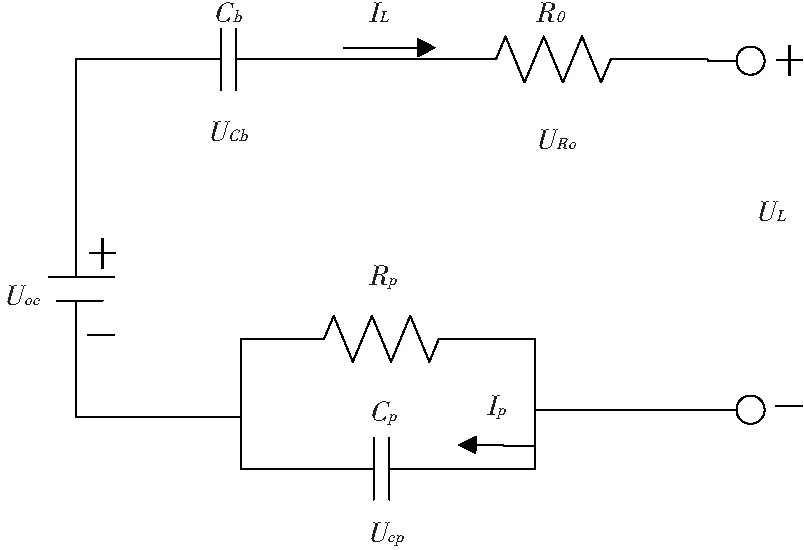
图1 PNGV等效电路模型
锂动力电池充放电倍率大,PNGV模型能较好反映其瞬态响应过程,可以体现电池的动静态特性,且结构简单、估算准确性高。UL用来描述电池的负载端电压,Ucp描述极化电容两端电压,Ip是流经极化电容的电流(规定放电时电流为正),Uoc是静置状态下的电池开路电压,用理想电压源代替,UCb表示的是电池放电时电容Cb上产生的电压变化,URo是欧姆电阻上的电压,用于描述阻抗特性压降。将PNGV模型中电池的端电压作为输出变量,两电容电压值作为状态输入变量,根据基尔霍夫电压定律、电容电压和电流关系可以得到:
(1)
因此PNGV模型的状态方程为:
(2)
影响电池SOC的因素有很多,主要与电池的温度、开路电压、电池欧姆内阻、极化内阻等因素相关,为简化识别模型参数,本文在常温条件下进行试验。通过复合脉冲(HPPC)实验对电池的动态性能进行测试,获得电池各项性能指标,并利用测试数据进行电池模型参数辨识。由于电池的开路电压与电池荷电状态存在一定的线性关系,首先通过实验测得电池端电压,利用PNGV电池数学模型表达式计算得到开路电压,经过处理可得到电池SOC,则模型静置状态下的开路电压与电池负载端电压的数学表达式为:
(3)
1.2 基于BP神经网络模型误差预测
锂离子电池是一个封闭式的电化学系统,实际运行工况复杂多变,其性能参数受工作电流、温度、使用寿命等因素,容易产生非线性、时变和不确定延迟情况,建立的电池模型存在结构困定、辨识困难、处理复杂等问题,因此不能够完全准确地描述复杂的电池动态系统。传统基于EKF的SOC估计方法要求对动态系统建立精确的模型,并且系统噪声必须服从高斯白噪声分布,实际上电池的系统噪声随机多变,以及搭建的电池模型受众多不确定性因素影响必然存在误差。而预测控制可以不必要求控制对象基于严格的数学模型,通过预测模型误差,针对不同的模型误差,采用不同的算法进行估计,可以有效消除由于噪声等因素造成较大模型误差而导致SOC估计的不准确性,这样可以提高荷电状态的预测精度。
电池模型误差与电池端电压、电流关系复杂,神经网络能够很好地逼近复杂的非线性映射关系,具有学习和适应不确定系统动态特性的能力,其算法主要是利用输入输出样本集进行相应训练。本文基于BP神经网络算法预测电池模型误差[16],将电池负载端电压和电流作为输入,电池模型误差作为输出,不需要精确预测电池的模型误差,只需得到电池模型误差大小,将电池模型误差模糊化为0和1的变量,当模型误差大于等于δ时,记为1;当模型误差小于δ时,记为0。则基于BP神经网络算法的模型误差预测表达式为:
Flagk=g(UL,k,iL,k)
(4)
其中:Flagk表示第k步预测的模型误差模糊化函数,其值在0和1之间;非线性函数g为神经网络函数;UL,k和iL,k分别为脉冲测试中第k步电池的负载端电压和流过电流的测量值。由文献[16]可知,利用BP神经网络算法来预测电池模型,并进行模糊化处理,其结果以μ为分界线,当μ≤Flagk≤1时,认为模型误差较大;而当0≤Flagk<μ时,认为模型误差较小。
当模型误差较小时,即0≤Flagk<μ,则测量噪声协方差Rk也比较小。模型可认为不受外界干扰,滤波器快速收敛,此时卡尔曼滤波增益Lk变大,滤波越振荡对滤波状态情况修正能力越强,令Rk等于一个较小值,采用EKF算法进行状态估计,增强滤波的收敛速度,从而提高SOC估计的准确性。当模型误差较大时,即μ≤Flagk≤1,相应的Rk变大。外界随机噪声对模型产生干扰,干扰越大时滤波器收敛变慢,滤波增益Lk变小,此时滤波越平滑对滤波状态修正能力减弱,可令Rk为无穷大值,Lk接近于0,采用HIF算法进行状态估计,可以减少由于噪声等不确定性因素造成的较大模型误差,克服Kalman滤波在随机信号干扰下会产生滤波发散的局限性,从而可以提高SOC的估计精度。
2 EKF-HIF算法
2.1 EKF算法
EKF算法是改进的卡尔曼滤波算法,用于非线性动态系统,将所建电池的状态空间模型线性化。利用卡尔曼滤波原理通过不断递推的方式更新数据,实现最小方差基础上系统状态SOC的最优估计,在线实时的给出理论值与真实值差值的估计范围。相比于其他滤波方法容易实现,可以修正初始值误差和抑制噪声,在满足条件的实现过程中能保持很好的精度。基本原理是根据上一时刻数据对某一时刻实验数据进行分析并与系统的理论值比较,选取理论值与真实值差值的最优值并计算误差协方差,同时对该时刻的各组数据进行实时更新并预测下一时刻系统理论上的状态变量值,这样经过反复地更新与选取,最后得到状态估计最优值。
EKF初始化后的算法如下:
(1) 线性状态空间方程:
xk+1=f(xk,uk)+wk
(5)
yk=g(xk,uk)+vk
(6)
定义:
(7)
(8)
(2) 初始化:令k=0,
(9)
(10)
(3) 迭代过程:令k=1,2,…
时间状态更新方程:
(11)
误差协方差时间更新方程:
(12)
卡尔曼增益:
(13)
状态估计更新方程:
(14)
误差协方差状态更新方程:
(15)
2.2 HIF算法
系统鲁棒性(Robust)是指允许系统承受不确定性,能够在各类噪声环境中尽量保持稳定状态的能力,具备系统鲁棒性的滤波称为鲁棒滤波,H∞滤波是其中实际应用最为广泛的算法之一。Kalman滤波需要建立精确的模型,滤波器模型也仅限于高斯噪声过程,在强非线性条件下会出现滤波发散现象,估计误差严重偏离。H∞滤波算法为解决存在建模误差系统,将H∞范数应用到滤波中,其设计思想是不以精确的噪声先验特性为先决条件,只需要假定噪声为有限的随机信号,可以在不确定的噪声环境下进行参数控制,实现最恶劣的情况下最小化估计误差。
HIF算法[17]如下:
(1) 线性离散时间状态空间方程:
(16)
定义:
(17)
(2) 初始化:令k=0,
先验状态估计:
(18)
先验协方差估计:
(19)
对称正定矩阵更新方程:
(20)
(3) 测量更新:
(21)
卡尔曼增益矩阵更新:
(22)
后验状态更新方程:
(23)
后验协方差状态更新方程:
(24)
3 基于模型误差的EKF-HIF联合估计算法
采用扩展卡尔曼滤波和H∞滤波联合估计算法,是利用EKF算法收敛较快、对初始值精度要求低,能在高斯白噪声过程对系统状态SOC做最小方差意义上的最优估计,具有较高的估计精度。HIF算法能够处理存在建模误差的系统,对系统参数的变化敏感性不强。具有较强的鲁棒性能,可以在不同噪声环境中维持估计误差范围的稳定,有效克服EKF算法在相同情况下SOC估计结果严重偏离的现象。原理是通过BP神经网络算法预测电池模型误差,根据模糊化函数对协方差Rk进行实时监测与修正,当预测的电池模型误差较小时,此时模型受外界干扰比较小,可令Rk为一个较小的常数值,采用EKF算法估计SOC,以保证该算法的收敛速度;当预测的电池模型误差较大时,外部干扰特性对模型的影响较为明显,令Rk为无穷大值,采用HIF算法估计电池SOC,可以有效消除由于外界干扰噪声等不确定性因素造成的估计误差,可以大大提高荷电状态SOC的估计精度,改善EKF估计方法在相同情况下发生偏离的状况。具体SOC估计流程如图2所示。
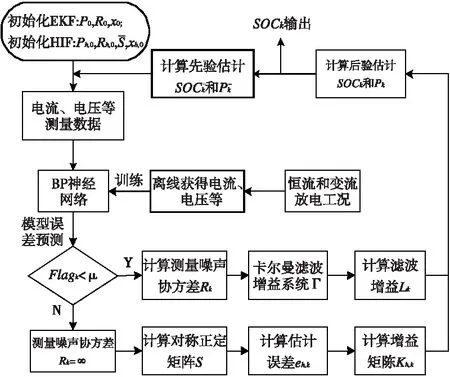
图2 EKF-HIF估计算法流程图
4 仿真实验
本文使用40 Ah的磷酸铁锂电池作为实验研究对象,在室温下进行HPPC测试实验,根据实验数据计算模型各项电路参数。利用电池模型的数学表达式在Simulink中建立PNGV等效模型,通过测试实验结果对模型参数进行辨识。同时为了检验所建锂电池模型的准确性,需要与实际工况下电流充放电得到的SOC值相比较。通过建立锂电池的放电模型,采用恒流放电、静置等工况模拟电池实际状况,分别对电池以0.5 C、1.2 C、1 C放电速率进行仿真实验,并与模型在变电流工况下的放电实验进行对比。实验结果如图3所示,由曲线图可以看出SOC试验结果和仿真结果的变化都成下降趋势,电池电势的快速和缓慢过程基本一致,说明建立的PNGV模型能够反应锂电池的动态状况。
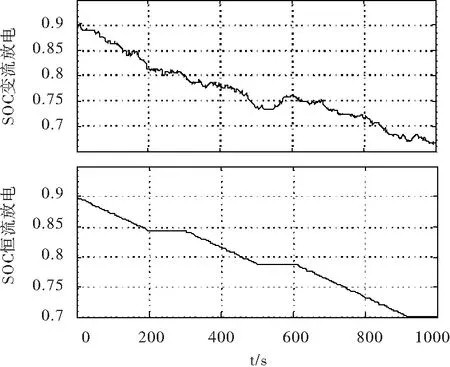
图3 恒流和变流放电实验波形
通过以上实验表明建立的PNGV电路模型可以对锂电池进行状态估计,为了提高SOC的估计精度,根据误差预测模型函数,在MATLAB上进行BP神经网络算法仿真实验,电池模型误差预测结果如图4所示。
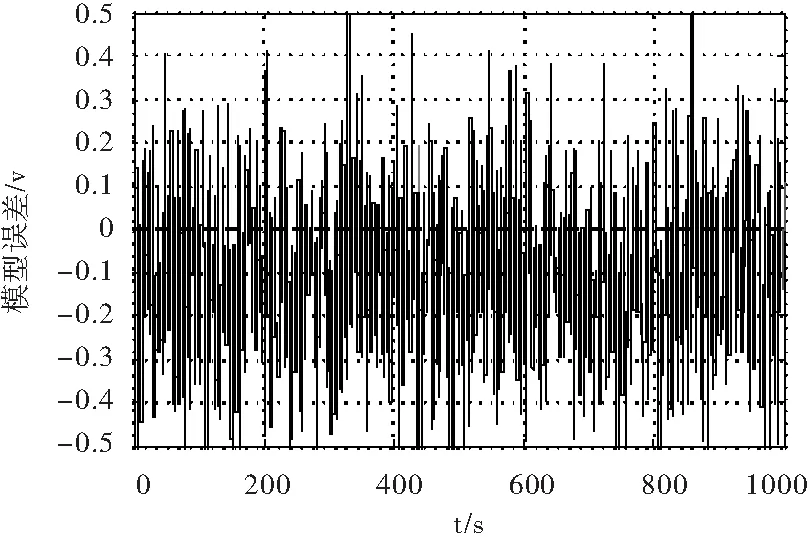
图4 基于BP神经网络的模型误差
根据图4,δ可取为0.01 V,模型误差大于等于0.01 V时,记为1;模型误差小于0.01 V时,记为0,为确定模型误差大小取μ=0.5作为模糊化分界线,可以得到当0.5≤Flagk≤1时,认为模型误差较大;而当0≤Flagk<0.5时,认为模型误差较小。由上文所得结果可知,当0≤Flagk<0.5时,采用EKF对SOC进行预测;当0.5≤Flagk≤1时,采用HIF对SOC进行预测。根据联合算法流程图,将测得的电池电流和电压数据运用EKF和HIF的迭代算法,在MATLAB中对电池SOC进行估计。
为了衡量该联合算法预测锂电池荷电状态SOC的准确性,使用传统的EKF估计算法进行对比实验。图5(a)给出了基于EKF和EKF-HIF的SOC估计误差,图5(b)给出了基于EKF-HIF的SOC估计误差局部放大的曲线图。
锂离子电池SOC估计误差表示SOC的理论预测值与实际参考值的差值,由图5(a)可以看出,传统EKF的SOC估计最大误差为5%;由图5(b)可以看出,EKF-HIF的SOC联合估计最大误差为1.1%。通过对比实验,从实验结果可以得到基于EKF-HIF的SOC估计方法无论在估计精度还是在收敛速度方面均明显优于传统EKF的SOC估计方法。
5 结束语
本文提出了一种基于模型误差EKF-HIF算法的SOC联合估计方法。该方法建立PNGV电池模型,通过实验验证了模型的有效性,同时为了更加精确地估计荷电状态SOC,需要减少由于系统随机噪声等不确定因素造成的估计误差,在传统EKF估计方法上进行了改进。利用BP神经网络算法预测模型误差并进行模糊化处理,根据不同的模型误差,采用EKF-HIF相结合的算法估计SOC。通过基于传统EKF的SOC估计方法对比实验,证明了EKF-HIF算法的优越性,表明该方法可以高效准确地对电池SOC进行估计。
[1] ZHANG J,LEE J.A review on prognostics and health monitoring of Li-ion battery[J].Journal of Power Sources,2011,196(15):6007-6014.
[2] 魏学哲,孙泽昌,田佳卿.锂离子动力电池参数辨识与状态估计[J].同济大学学报:自然科学版,2008,36(2):231-235.
[3] PILLER S,PERRIN M,JOSSEN A.Methods for state-of-charge determination and their applications[J].Journal of Power Sources,2001,96(1):113-120.
[4] 麻友良,陈全世,齐占宁.电动汽车用电池SOC定义与检测方法[J].清华大学学报:自然科学版,2001,41(11):95-97.
[5] SANTHANAGOPALAN S,WHITE R E.State of charge estimation for electrical vehicle batteries[C]//Proceeding of 2008 IEEE International Conference on Control Applications(CCA2008),San Antonio,TX,USA,September 3-5,2008:690-695.
[6] SANTHANAGOPALAN S,WHITE R E.State of charge estimation using an unscented filter for high power lithium ion cells[J].International Journal of Energy Research,2010,34(2):152-163.
[7] 林成涛,陈全世,王军平,等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报:自然科学版,2006,46(2):247-251.
[8] 雷肖,陈清泉,刘开培,等.电动车蓄电池荷电状态估计的神经网络方法[J].电工技术学报,2007,22(8):155-160.
[9] 雷肖,陈清泉,刘开培,等.电动车蓄电池荷电状态估计的支持向量机方法[J].中国电机工程学报,2008,28(18):114-118.
[10] 徐颖,沈英.基于改进卡尔曼滤波的电池SOC估算[J].北京航空航天大学学报,2014,40(6):855-860.
[11] 何洪文,熊瑞.基于滑模观测器的锂离子动力电池荷电状态估计[J].吉林大学学报:工学版,2011,41(3):623-628.
[12] 张洁.基于粒子滤波算法的电动汽车剩余电量动态估计研究[D].北京:北京交通大学,2012.
[13] 陈息坤,孙冬,陈小虎.锂离子电池建模及其荷电状态鲁棒估计[J].电工技术学报,2015,30(15):141-147.
[14] 王莉.基于H∞滤波器的锂电池SOC估计与功率预测方法的研究[D].天津:天津大学,2015.
[15] MOTLOCH C G,BELTJ R,CHRISTOPHERSEN J P, et al.PNGV Battery Performance Testing and Analyses[J].Advanced Battery Technology,2002(6):22-23.
[16] 商云龙,张承慧,崔纳新,等.基于模糊神经网络优化扩展卡尔曼滤波的锂离子电池荷电状态估计[J].控制理论与应用,2016,33(2):212-220.
[17] YU Q,XIONG R,LIN C,et al.Lithium-ion battery parameters and state-of-charge joint estimation based on H-infinity and Unscented Kalman Filters[J].IEEE Transactions on Vehicular Technology,2017,66(10):8693-8701.

