基于最小二乘-广义层次分析法的次级地表移动参数反演

吴作启，陈清通，李 健

(1.煤炭科学技术研究院有限公司 安全分院，北京 100013； 2.煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院)，北京 100013； 3.北京市煤矿安全工程技术研究中心，北京 100013)

矿山的地下采掘活动将对其周围岩体直至地表产生采动影响。这种采动影响使岩体本身及岩体内的地下工程结构物、含水地层、地面地形、地貌、耕作地、农作物、植被、建(构)筑物、水体以及自然和人工边坡、陡崖等产生变形和损害，影响工农业生产建设和人民生活[1]。

国际上对采矿损害现象的大规模研究始于19世纪40年代，我国在煤矿区进行地表下沉观测工作最早是在1954年的扎赉诺尔矿区。进入20世纪60年代后，随着矿井生产的不断发展，国内主要采煤矿区开展了大量的地下采煤引起的地表移动观测、观测资料整理与分析、地表移动规律及采场覆岩破坏规律理论研究等工作。经过矿山测量工作者和开采沉陷领域的专家、学者几十年的努力，我国各大矿区基本都已具有了本矿区的地表移动监测资料和参数体系。郭文兵等建立了地表移动观测站、地表下沉系数影响因素和地表下沉系数的人工神经网络模型，探寻出一种确定地表下沉系数的方法[2-3]；谭志祥等以兖州矿区地表移动参数为例对综放采面地表变形预计参数进行了研究[4]；王正帅等提出了概率积分法参数识别的多尺度核偏最小二乘回归方法，并得到了较高精度的预测结果[5]；张广伟等根据采动岩体结构演化特征建立了岩体运动破坏模型，得出了下沉系数与采深和岩性的函数关系[6]；郭文兵等分析了条带开采条件下影响地表移动参数的因素，建立了适用于条带开采的地表移动预计参数的计算公式[7]；周大伟等运用主成分回归分析的方法研究了概率积分法参数的确定，提高了预计的精度[8]；李培现等基于支持向量机建立了地表移动的概率积分法参数动态时序预报模型，并进行了实测数据验证[9]；王磊等对山区地表沉陷预计模型进行了修正并提出了相应的参数求取方法[10]；朱广轶等提出了刻画概率积分法预计采空区对地表沉陷预计的时间和空间变化规律的坐标-时间函数，并在函数中嵌入了岩移参数[11]。煤炭行业进入市场经济后，多数矿井由于生产接续需要，已不再开展首采面地表移动观测站的持续观测工作，转而进行井田范围内跨越多个工作面、大范围的监测线的沉降监测工作。由于缺少地表移动长期影响的观测数据和计算参数，特别是地表移动稳定期后的计算参数，在对原有开采影响的评价中，参数的选取存在较大差异，也容易引起争议[12]。

实践证明：使用矿区或者类比邻近矿区的地表移动参数得到的设计方案与实际地表移动情况往往存在较大偏差，而本矿井布设的多工作面大范围的沉降监测线的监测结果更符合本矿井的实际采动损害情况。因此，在本矿井没有首采面地表移动参数的条件下如何充分、合理地利用现有的地表移动观测资料进行本矿井的相关规划设计工作具有重大的现实意义。

1 次级地表移动观测站

地表移动观测站是指开采影响范围内的地表、岩层内部或其他研究对象上，按一定要求设置的一系列互相联系的观测点。在开采过程中，根据需要定期观测这些测点的空间位置及其相对位置的变化，以确定各测点的位移和点间的相对移动，从而掌握开采沉陷的规律。标准的地表移动观测站应满足以下要求：观测线应在地表移动盆地的主断面上；观测期间不受其他开采工作面的采动影响；观测线的长度要大于地表移动盆地的范围；根据开采深度和设站目的设定观测线上测点的密度；观测站的控制点要设在移动盆地范围以外，埋设要牢固。

现行矿井生产接续设计紧凑，基本无法实现首采面的连续观测至地表稳定，取而代之的是跨越多个工作面且不一定设在地表移动盆地主断面上的沉降监测线，此类监测线不满足标准地表移动观测站的基本要求，所测数据大多以监测点处地表的下沉值为主。此类不满足标准地表移动观测站的地表下沉监测线称为次级地表移动观测站。次级地表移动观测站虽不具备标准的地表移动观测线的基本要求和所有功能，但对于没有首采面标准地表移动观测站的生产矿井而言，次级地表移动观测站的监测数据仍然是极其珍贵且仅有的实测资料，其测量结果及相关地表移动参数完全符合自身矿井的实际情况。尤其在进行保护煤柱的设计、村庄下采煤评价和采空区的采动影响范围界定等涉及地表移动参数的相关规划设计工作时，采用本矿井的次级地表移动观测站得出的地表移动参数作为依据更加准确可信。

2 基于最小二乘-广义层次分析法的次级地表移动参数反演模型

2.1 次级地表移动参数反演模型

次级地表移动参数反演模型中定义目标层为：决策最优地表移动参数(下沉系数q、水平移动系数b、开采影响传播角系数k、主要影响角正切tanβ和拐点偏移距s)[13]；准则层为使用不同排列组合的地表移动参数进行概率积分计算得出的监测点位置的有效变形值，有效变形值为通过实际测量获得的监测点下沉值、水平移动值、倾斜值、曲率变形值、水平变形值中的一项或者多项，择优准则为最小二乘法；方案层为地表移动参数中涉及的各参数的不同取值的排列组合，方案的数量取决于所设定的各参数备选区间(例如下沉系数q∈[0，1])和挑剔步长(例如下沉系数的挑剔步长可设置为0.01)，挑剔步长越小，则反演结果越精确，相应的计算量也越大。模型设计流程如图1所示。

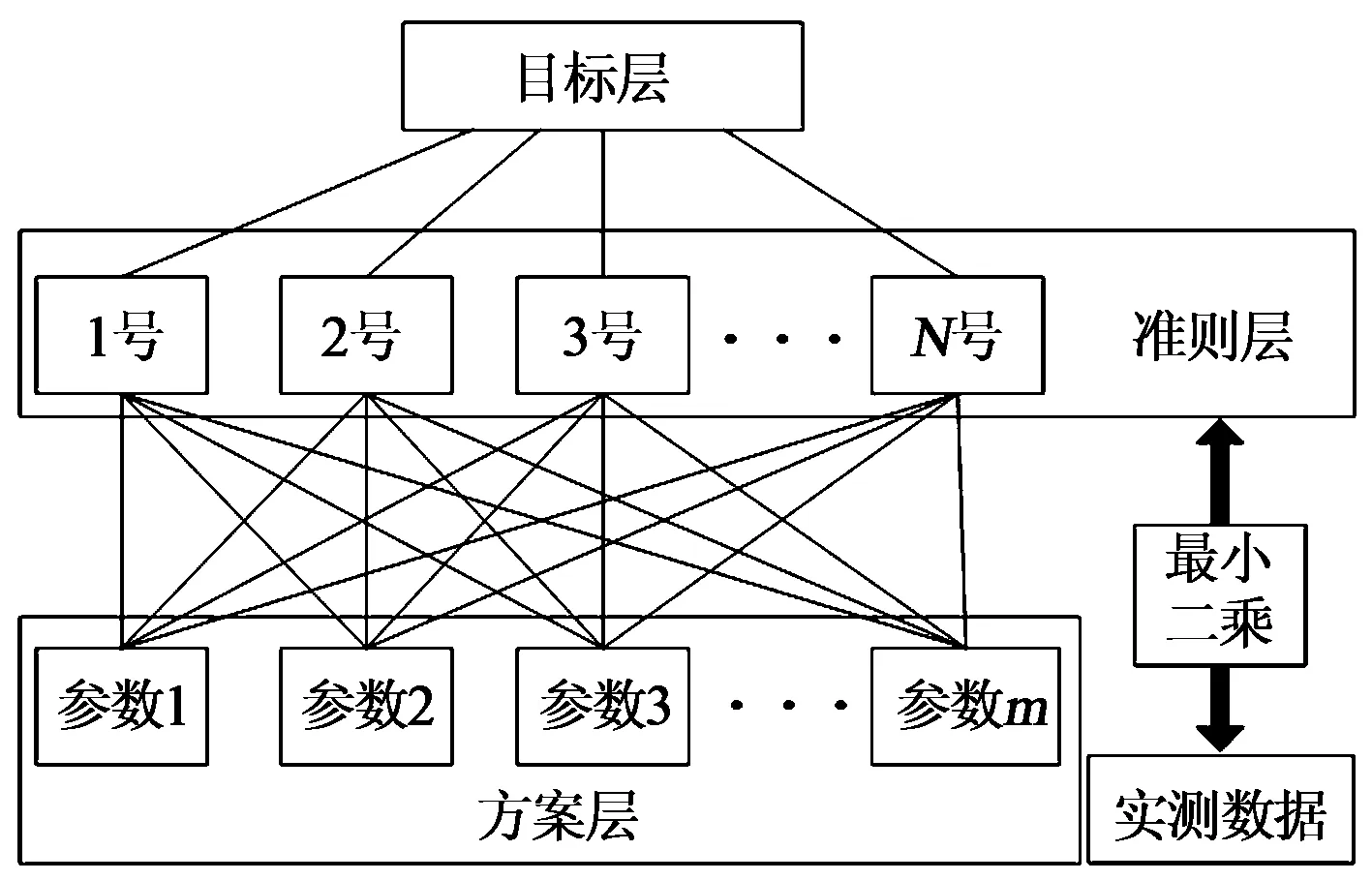
图1 参数反演模型设计流程

2.2 次级地表移动参数反演模型的计算与实现

根据我国《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》[13]使用概率积分法对地下采空区影响下的地表任意点的下沉值、倾斜值、曲率值、水平移动值和水平变形值进行计算，计算方法如公式(1)～(9)所示。

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中，Wcm=m·qcosα，mm；Ucm=b·Wcm，mm；m为煤层开采厚度，mm；q为地表下沉系数；b为水平移动系数；θ0为开采影响传播角；r为等价计算工作面的主要影响半径，r=Hd/tanβ；Hd为等价开采影响深度；tanβ为主要影响角正切；ix(x，y)和iy(x，y)分别为沿煤层走向和倾向方向的倾斜，mm/m；Kx(x，y)和Ky(x，y)分别为沿煤层走向和倾向方向的曲率，10-3/m；Ux(x，y)和Uy(x，y)分别为沿煤层走向和倾向方向的水平移动，mm；εx(x，y)和εy(x，y)分别为沿煤层走向和倾向方向的水平变形，mm/m。

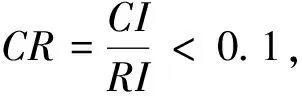
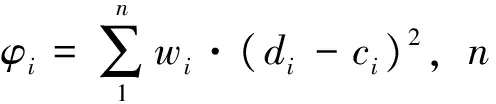
3 矿区次级地表移动参数反演分析

3.1 矿区工程概况

某煤矿区域地表地势平坦，地面标高为+35～+42m之间，西南略高，区域第四系冲积层普遍覆盖，厚度为51.85～89.81m，平均63.7m。开采水平标高为-60～-650m，可采煤层为二叠系下统下石盒子组1，2煤层和山西组7，9煤层，石炭系上统太原组20，21煤层。区域内有F3，F4，F47，F51等断层分布。采用立井多水平上、下山开拓方式，开采顺序自上而下进行工作面回采：急倾斜部分为走向小阶段爆破采煤法；缓倾斜部分为走向长壁采煤法，炮采，全部垮落法管理顶板。现主采山西组7，9煤层，其中7煤层开采时间始于2005年1月，采厚3～4m，倾角65～75°，目前最大开采深度为386m。山西组9煤层开采始于2006年3月，采厚1.8～2.5m，倾角65～70°，目前最大开采深度为237m。该矿未设置标准地表移动观测站，但为监测矿内运煤铁路沉降情况，沿铁路线布设了铁路沉降监测线，自2005年3月5日至2013年12月19日，共开展了11次水准观测，获得了14个有效监测点的高程持续变化资料。该铁路沉降监测线属于典型次级地表移动观测线，监测点下沉情况如图2所示。

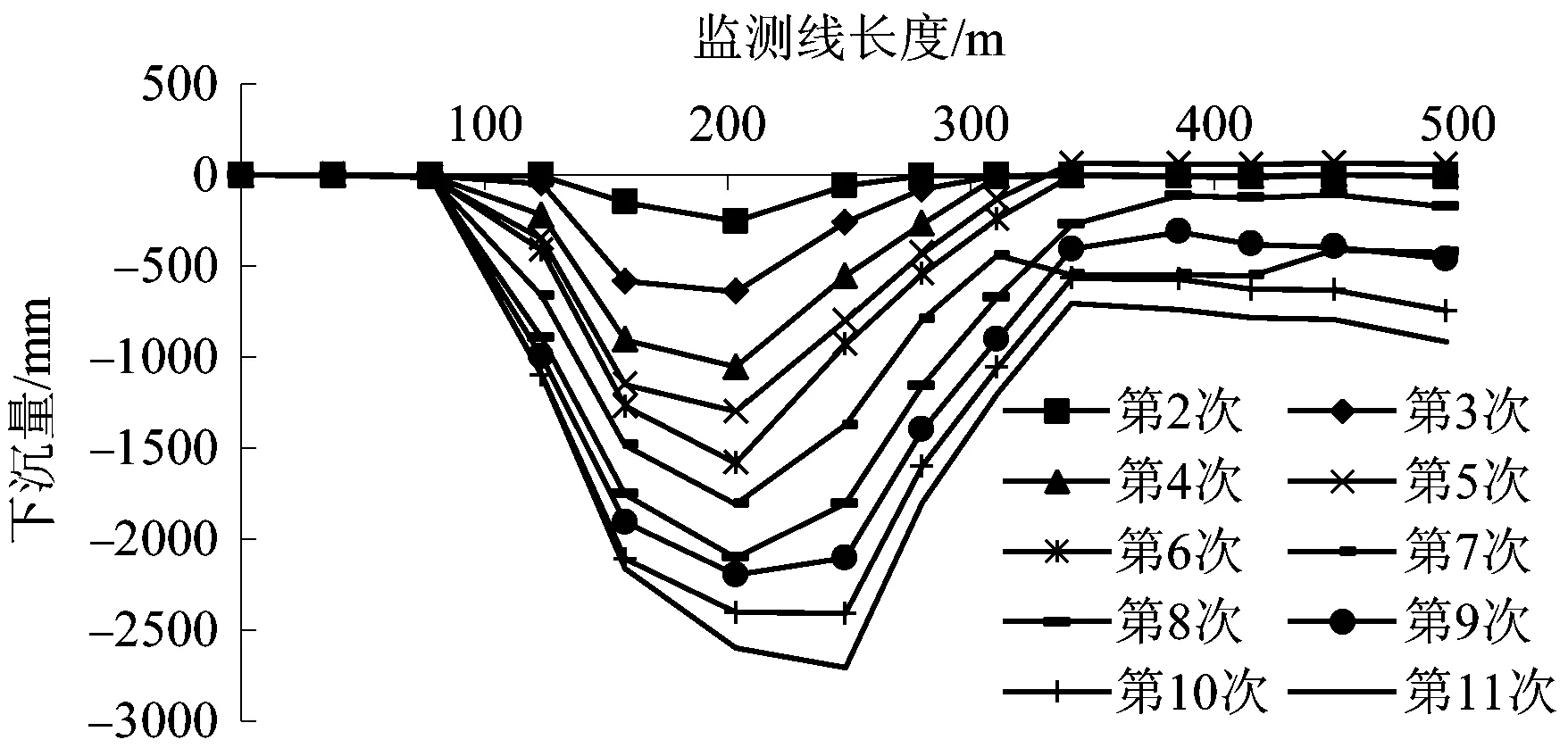
图2 次级地表移动观测线监测点曲线

位于该煤矿采空区下山方向的村庄房屋于2011年上半年开始出现明显变形与破坏。同时介于村庄与采空区的耕地中出现了一条有明显落差的地表裂缝，实测结果表明：地表裂缝呈北东～南西展布，总长约848m，最大开裂宽度0.25m，最大台阶落差1.8m。裂缝局部落差及房屋损坏情况如图3所示。次级地表移动观测线、地表裂缝与村庄和采空区的相对位置关系如图4所示。

图3 地表裂缝下沉台阶及居民区房屋损坏情况缩略图

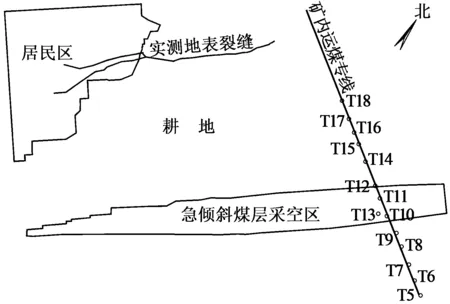
图4 采空区、居民区、地表裂缝和次级地表移动观测站相对位置关系示意

3.2 次级地表移动参数反演及分析

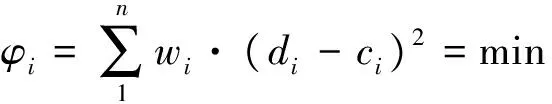
图5 急倾斜煤层采空区形成的地表下沉等值线

下沉/mm倾斜/(mm·m-1)水平移动/mm水平变形/(mm·m-1)曲率变形/(10-3·m)27602451265+634，-2970+009，-059

根据反演得出的地表移动参数计算出的采煤沉陷结果可知，计算得出的地表最大下沉值与实测地表最大下沉值的量以及平面位置吻合，矿区居民区东南部损坏民房和地表裂缝均处于急倾斜煤层采煤沉陷范围之内。急倾斜煤层采空区位于逆断层F51下盘方向，且急倾斜煤层采空区影响范围包括了断层F51的地表露头位置，当急倾斜煤层开采到一定深度，采动引起顶板岩层以悬臂梁弯曲形式产生移动与变形，诱发F51断层面的变形集中，导致断层隐伏露头对应地表处产生西北高、东南低的台阶状裂缝，地表裂缝处变形剧烈且集中，地表裂缝远离采空区一侧地表变形及房屋损坏情况则明显减弱，此特征与现场实测地表裂缝的症状完全吻合。采空区、断层及地表裂缝相对位置关系如图6所示。因此，该区域台阶状地表裂缝的形成与急倾斜煤层的采掘活动有关系。

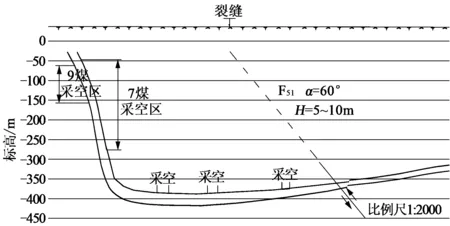
图6 断层F51、地表裂缝及采空区相对位置关系

4 结 论

(1)建立了基于最小二乘-广义层次分析法的次级地表移动参数反演模型，通过MATLAB编程实现了参数反演的计算机自动计算，为没有标准地表移动观测站的煤矿提供了一种科学合理的利用次级地表移动观测站求取地表移动参数的方法。

(2)通过对某煤矿次级地表移动观测站监测数据进行地表移动参数反演，计算得出了该矿的地表移动参数并应用该套参数计算了该矿急倾斜煤层开采的采动影响范围及地表变形量。通过现场实测验证了地表移动参数的正确性。

(3)结合地表采动影响范围和地表变形量，解释了该煤矿居民区房屋损坏的形成原因，揭示了地表裂缝的形成原因，为规避矿区灾害和保证矿区人民生命财产安全提供了技术依据。

[1]范学理，刘文生，等.中国东北煤矿区开采损害防护理论与实践[M].北京：煤炭工业出版社，1998.

[2]郭文兵，邓喀中，邹友峰.地表下沉系数计算的人工神经网络方法研究[J].岩土工程学报，2003，25(2)：212-215.

[3]郭文兵，邓喀中，邹友峰.条带开采下沉系数计算与优化设计的神经网络模型[J].中国安全科学学报，2006，16(6)：40-45.

[4]谭志祥，邓喀中.综放面地表变形预计参数综合分析及应用研究[J].岩石力学与工程学报，2007，26(5):1041-1047.

[5]王正帅，邓喀中.概率积分法参数辨识的多尺度核偏最小二乘回归方法[J].岩石力学与工程学报，2011，30(S2)：3863-3870.

[6]张广伟，李凤明，李树志，等.基于岩体破裂规律的下沉系数变化[J].煤炭学报，2013，38(6)：977-981.

[7]郭文兵，邓喀中，邹友峰.条带开采地表移动参数研究[J].煤炭学报，2005， 30(2)：182-186.

[8]周大伟，安世凯，张 静，等.概率积分参数选取的主成分回归分析[J].辽宁工程技术大学学报(自然科学版)，2013，32(11): 1528-1532.

[9]李培现，谭志祥，闫丽丽，等.基于支持向量机的概率积分法参数动态时序预报[J].煤炭学报，2011，36(S2):380-385.

[10]王 磊，郭广礼，王明柱，等.山区地表移动预计修正模型及其参数求取方法[J].煤炭学报，2014，39(6):1070-1076.

[11]朱广轶，沈红霞，王立国.地表动态移动变形预测函数研究[J].岩石力学与工程学报，2011，30(9)：1889-1895.

[12]张华兴.煤矿开采损害的评价与防护[J].煤矿开采，2015，20(3)：1-2， 20.

[13]国家安全监管总局、国家煤矿安监局、国家能源局、国家铁路局.《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程》[S]. 北京： 2017.