基于ANSYS的钢-混凝土体外预应力连续组合梁有限元分析

刘 超

（苏交科集团股份有限公司，江苏 南京 210019）

钢-混凝土连续组合梁可以充分发挥混凝土的抗压性能与钢材的抗拉性能，是一种性能优良的结构形式。体外预应力组合梁是将预应力钢筋布置在组合梁的外部，以提高桥梁刚度和承载力的一种结构形式［1］。20世纪初，国外开始了对组合梁结构的研究和应用，20世纪50年代，预应力组合梁出现并得到应用，20世纪90年代，我国开始了对于此种结构形式的研究工作。目前理论分析和工程应用较少，很多理论问题亟待解决，传统的试验研究方法耗费大、周期长，不适应现代科研的要求［2］。因此，本文利用有限元软件AYSYS对预应力钢-混凝土组合连续梁桥应力增量、滑移以及剪力滞效应等力学行为进行分析，以期为工程技术人员提供参考。

1 组合梁结构有限元建模

1.1 单元选择

钢筋采用LINK10单元，LINK10是一种杆件单元，能够较好地模拟受压或者受拉的构件；混凝土采用SOLID65单元，SOLID65是一种实体单元，能够合理地模拟3D实体混凝土；钢梁采用SHELL181单元，SHELL181是一种壳体单元，对于工字钢一般采用此单元进行模拟；抗剪连接件采用COMBIN39单元，COMBIN39是一种非线性的弹簧单元，可以用来模拟单向变形。

1.2 试验模型结构尺寸

以文献［2］试验试件为原型，利用ANSYS建立与试验等尺寸模型，如图1所示。试验梁总长L=6 500 mm，总共两跨，每跨3 000 mm，距两端250 mm处约束竖向位移，跨中约束竖向和水平位移；钢梁腹板高200 mm，上下翼缘板厚度分别为300 mm、200 mm，厚度均为6 mm；混凝土梁厚100 mm，宽800 mm；钢梁和混凝土之间采用抗剪螺栓连接，共布置64个。

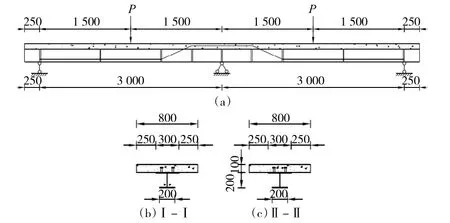
图1 试验梁尺寸及加载方式（单位：mm）

1.3 材料性质

钢梁为Q345QE型钢，弹性模量为2.0×105N/mm2，密度为7 800 kg/m3，屈服强度为fy=345 MPa，泊松比vc为0.3。混凝土立方体抗压强度标准值fcu，k=40 MPa，单轴抗压强度fcu=26.8 N/mm2，弹性模量为3.25×104N/mm2，轴心抗拉强度标准值ftk=2.39 N/mm2，张拉开裂的剪力传递系数βt=0.5，闭合裂缝的剪力传递系数βc=0.95。

钢筋为HRB335，试验测定屈服强度为fy=300 MPa，采用BISO模拟［3］，泊松比vc为0.3。

体外预应力筋为2根1×3-10.8-1860钢绞线，张拉预应力为58.8 kN，弹性模量为1.95×105N/mm2，泊松比vc为0.3。预应力钢筋的初应变：

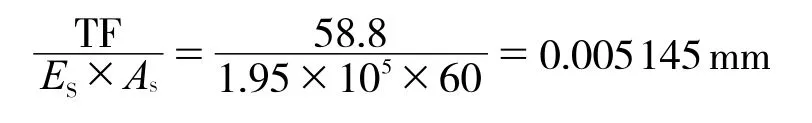
式中：TF为初张拉力；ES为弹性模量。

2 模拟计算结果与试验比对

2.1 沿高度方向滑移应变比对

图2与图3分别为试验梁加载过程中与ANSYS模拟的加载过程中，跨中L/4截面应变情况。对比图2与图3可以看出，数据与曲线基本吻合，说明有限元模型是可靠的，可以代替部分试验研究组合梁的力学性能。

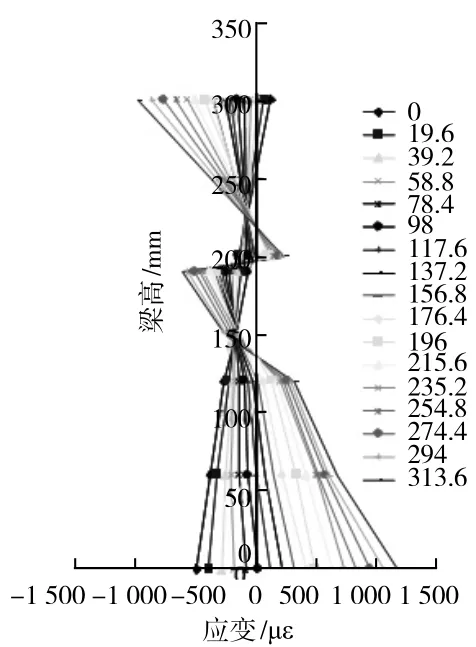
图2 试验不同加载级别跨中L/4截面应变分布

图3 ANSYS不同加载级别跨中L/4截面应变分布

2.2 挠度计算比对

挠度计算结果如表1所示，由表1可知，有限元计算结果与试验结果误差不大，进一步证明了本模型的可靠性。

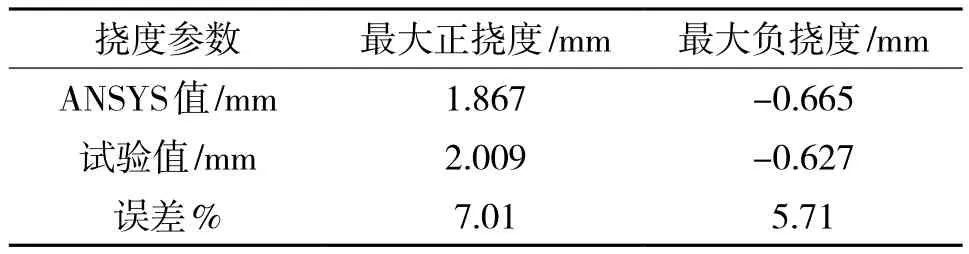
表1 施加预应力的挠度对比

3 实桥模型受弯性能分析

某钢-混凝土组合梁桥位于河北省107国道，设计荷载为公路I级，总长为75 m，宽度为20 m，混凝土强度等级为C50，钢梁为Q345E，钢绞线采用1×7-15.7-1860。利用本文的建模方法建立有限元模型，对其预应力增量、滑移性能以及剪力滞效应进行了分析研究。有限元模型如图4所示。

图4 总跨度75 m有限元模型

3.1 预应力增量计算

连续组合梁应力增量的计算较简支梁复杂，而简化计算方法的计算精度不高［4］，本文改进计算方法，假定组合梁受力过程中各种材料都处于弹性阶段，计算简图如图5所示。

在两跨跨中分别施加大小相同荷载，该结构体系为二次超静定结构，根据变形条件可得：

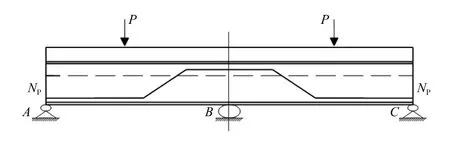
图5 计算简图

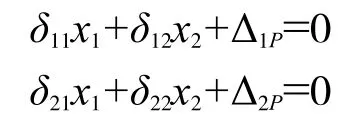
式中：δij为虚变形；Δ为虚变形。

由虚功原理：

式中：Mi、Mj为弯矩；ΔNi、ΔNj为轴力；A为截面面积；EI为截面刚度。

各参数结果为：

式中：Eps为体外预应力筋弹性模量；Aps为体外预应力筋面积；L为梁长，m=n=L/2；e为偏心距，b=e；c=e+e1L1/L；d=e1（1-L2/L1）。

根据以上参数，可以求得ΔN和M的值：

利用公式计算的预应力增量与ANSYS模拟计算对比如图6所示。从图6的数据可以看出，理论计算结果与有限元计算结果基本稳和，可以认为本文推导的理论计算公式是可靠的，可以利用本公式进行相应的计算。

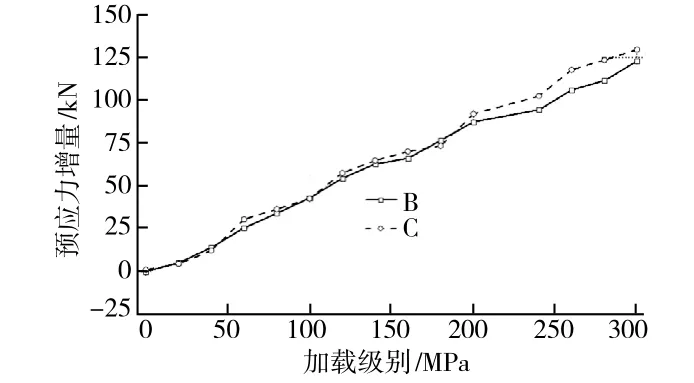
图6 体外预应力增量计算值与ANSYS数值对比

3.2 滑移分部规律

由于组合梁截面之间采用抗剪连接件连接，发生变形的时候，混凝土和钢梁之间不可避免地会发生相对位移，即滑移现象，为减小滑移，提高承载力，需对梁长方向的滑移分布进行研究。图7给出了梁长方向的滑移分布。

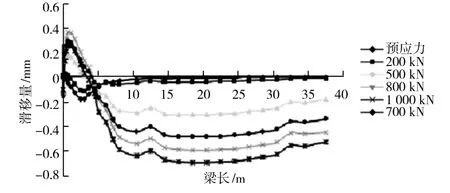
图7 不同荷载作用下梁长方向的滑移量分布

由图7可以看出，当不同的荷载作用时，组合梁的滑移现象将会有所改变，当只有预应力作用时，其最大的滑移量为0.182 mm，出现在距离梁中支座的3.5 m处，在梁端产生的滑移量几乎为零。当外荷载逐渐增加时，滑移量出现先减小后向相反的方向增大的趋势，其主要原因是施加的外荷载抵消了部分的预应力作用。总体上可以看出，滑移发展规律明显，并且最大滑移量没有出现在梁端的位置。

3.3 剪力滞效应分析

剪力在传递时，会出现滞后的现象，成为剪力滞效应。利用有限元模型对组合梁横截面的剪力滞效应进行了计算模拟，跨中及中支点计算结果如图8和图9所示。

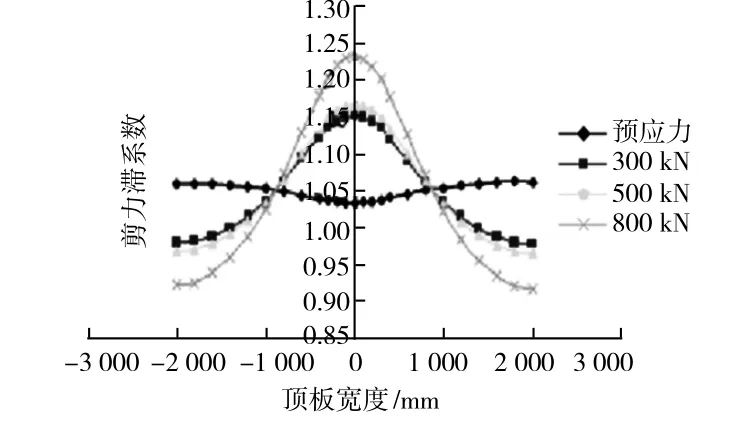
图8 不同荷载下中支点L/2处截面混凝土顶板剪力滞沿横向分布曲线

由图8与图9可以得出，外荷载作用下，组合梁出现明显的剪力滞效应，在预应力作用下出现的是负剪力滞效应。施加外荷载以后，负剪力滞将逐渐地变为正剪力滞，而且随着外加荷载的增大，剪力滞效应也更加明显。

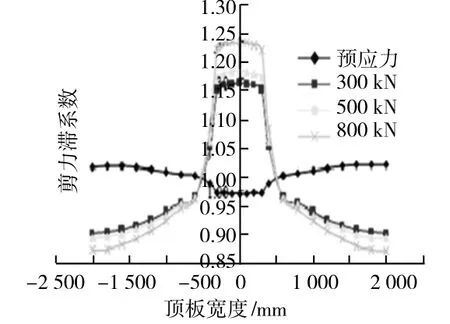
图9 不同荷载下中支点L/4处截面混凝土顶板剪力滞沿横向分布曲线

4 结论

（1） 采用ANSYS建立和试验等尺寸的模型，其计算结果与试验数据基本吻合，验证了所建模型的正确性，可以用来替代部分的试验来研究组合梁的力学性能。

（2） 提出了预应力筋增量的计算公式，并与有限元模型计算的结果进行对比，验证了公式的正确性。

（3） 在不同的外荷载作用下，组合梁出现的滑移现象有所变化。随着荷载增加，滑移量绝对值减小然后再逐渐增大，最大滑移量并没有出现在梁端，因此，可根据本文的曲线适当地增减交界面处的栓钉数量，从而减小滑移量，提高刚度和承载力。

（4） 施加外荷载后，组合梁将出现明显的剪力滞效应，只有预应力的情况下，组合梁出现的是负剪力滞，当施加外荷载后，负剪力滞逐渐地变成了正剪力滞，而且随着荷载的增大剪力滞效应越明显。

［1］朱劲松，朱先存.钢筋混凝土桥梁疲劳累积损伤失效过程简化分析方法［J］.工程力学，2012，29（5）：107-114.

［2］何珊瑚，窦超.拱形钢管混凝土结构实用计算方法［J］.工程力学，2012（S1）：162-165.

［3］聂建国，陶慕轩，吴丽丽，等.钢-混凝土组合结构桥梁研究新进展［J］.土木工程学报，2012（6）：110-122.

［4］陈世鸣，孙森泉，张志彬.体外预应力钢—混凝土组合梁负弯矩区的承载力研究［J］.土木工程学报，2005（11）:14-20.

［5］宗周红，郑则群，房贞政，等.体外预应力钢—混凝土组合连续梁试验研究［J］.中国公路学报，2002（1）：47-52.

［6］房贞政.预应力结构理论与应用［M］.北京：中国建筑工业出版社，2005.