基于因子图的USV位置估计算法

孙 鑫，姜 静

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

随着各国对海洋的探索，无人水面航行器(unmanned surface vehicle,USV)是近些年伴随着军事需求而新兴的产物。军事方面，出于维护安全，在执行扫雷、侦查、监测等任务时，USV具有很大优势；民用方面,USV能减少人力资源，提高船舶航行安全[1]，并可以作为连接无人机与水下航行器的移动水面通信节点，在未来开启海陆空全方面协同作战中起着不可或缺的重要作用。随着USV在各方面广泛的应用，人们对其性能要求越来越高，如高机动下的自主避障，复杂海况下的自主航行等；USV自身准确的位置信息是完成以上各种功能的基础条件。随着导航技术的不断发展，多传感器组合导航已经逐渐成为各种复杂环境下长时间高精度导航的主要方式[2-3]。文献[4-5]中以GPS和罗经为导航传感器，基于USV的二维平面运动学模型,利用扩展卡尔曼滤波(extended Kalman filter,EKF)算法对USV的速度和位置估计。但EKF算法只能对当前时刻的状态进行估计，当系统存在时间延迟，传感器采样周期不一致等问题时，需要增加计算量，降低定位精度，且在弱噪声情况时，滤波效果不佳[6]，所以本文提出一种新的USV定位方法，即基于因子图的USV位置估算算法，仿真结果表明本文所提算法可以准确估计USV的位置信息，而且在弱噪声环境下效果更佳。

1 USV二维平面运动模型及其线性化

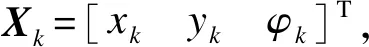
(1)

式中wk和Vk分别为USV的偏航角速度和行驶速度。

(2)

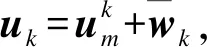
(3)

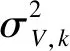
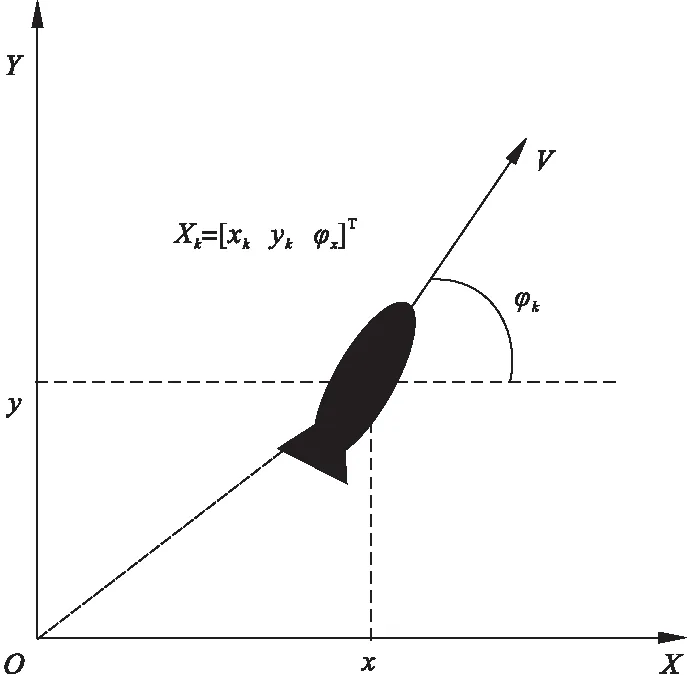
图1 USV二维空间运动模型

所以USV的二维运动学方程可简写为

(4)

式中

(5)

(6)

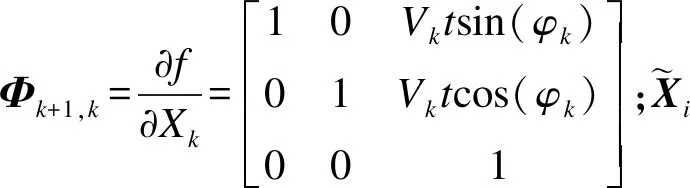
把式(4)展开可得线性化后的USV运动学方程为

(7)

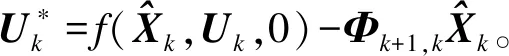
由此可得状态转移函数为

(8)

在k+1时刻，GPS观测的USV位置信息可用观测方程表示为

(9)

协方差矩阵为

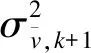
由此可得观测过程更新函数为

p(Zk+1|Xk+1)=N(Zk+1;Hk+1Xk+1,Rk+1)

(10)

2 因子图与和积算法

20世纪90年代,因子图由F R Kschischang等从Wiberg图、Tanner图等模型的基础上推广而来，其后被用做研究信道估计、解码及迭代接收机技术的通用工具[8]。因子图模型具有很强的灵活性，能够实现传感器的即插即用，已经在导航领域受到广泛关注[9]。因子图是一种二向图，可将一个复杂多元的全局函数问题拆分为多个简单的子函数的积。因子图包括两种节点：变量节点和函数节点。函数节点代表的是局部函数，而与其相连的那些变量是其自身相关的自变量[10]。

f(X1,X2,X3,X4)是包含四个变量的全局函数，f1、f2、f3是其组成的三个局部函数，全局函数与局部函数之间的关系为f(X1,X2,X3,X4)=f1(X1)f2(X2)f3(X1,X2,X3,X4),具体的因子图模型如图2所示，图中每一条边都连接着一个变量节点(圆圈)和一个函数节点(方框)；其中fi为函数节点，Xj为变量节点，BI(fi,Xj)表示函数节点fi到变量节点Xj的置信度信息，BI*(Xj,fi)表示变量节点Xj到函数节点fi的置信度信息，i=1,2,3，j=1,2,3,4。

基于因子图的问题是通过在因子图中的变量节点和函数节点之间传递“置信度信息BI(Belief Information)”解决的，在经过多次迭代后，得到收敛解。置信度信息为随机变量的均值和方差[11]。整个过程通过和积算法[12]实现。以图2为例，置信度信息在相邻节点间传递需满足以下规则。

(1)从变量节点传递到函数节点的置信度信息是所有来自其它相邻函数节点到达这一变量节点的置信度信息的乘积。

BI*(X1,f3)=BI(f1,X1)BI(f2,X1)

(11)

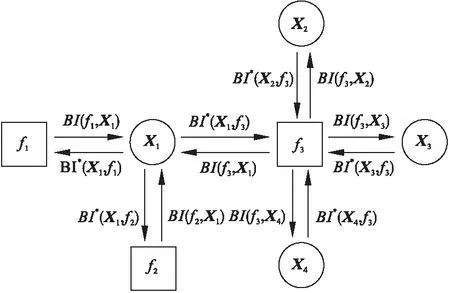
图2 因子图模型

(2)函数节点传递到变量节点的置信度信息是所有相邻变量节点传递给该函数节点置信度信息与包含这些变量的函数的乘积，然后再对所有除此变量外的相关变量做积分所得。

BI(f3,X3)=

BI*(X2,f3)BI*(X4,f3)dX1dX2dX4

(12)

(3)由以上两个规则可推导出，变量节点的置信度信息等于所有相邻的函数节点到该变量节点的置信度信息的乘积。

BI(X1)=BI(f1,X1)BI(f2,X1)BI(f3,X1)

(13)

上述规则为和积算法的基本思路，通过利用和积算法对变量的计算，实现全局问题的局部求解，显著降低了算法的复杂度。

3 基于因子图的USV位置估计算法

由第2节中式(7)和式(9)可以得知，USV位置估计的过程是由GPS观测值来估计的，所以该模型可以写成条件概率密度函数f(X1,…,Xk+1|Z1,…,Zk+1)，而且k+1时刻的状态向量Xk+1只与k时刻的状态变量Xk有关，而与k时刻以前的状态变量无关；k+1时刻的GPS观测值只与状态变量Xk有关，满足隐马尔科夫模型。所以条件概率密度函数可以因式分解为

f(X1,…,Xk+1|Z1,…,Zk+1)

(14)

式(14)的因子图见图3，其中函数节点为f(Xi+1|Xi)、f(Zi|Xi),i=1,2,…,k；变量节点为Xi、Xi,i=1,2,…,k+1。假定图3中的所有变量节点都服从高斯分布，均值为A，协方差矩阵为B2。

(15)

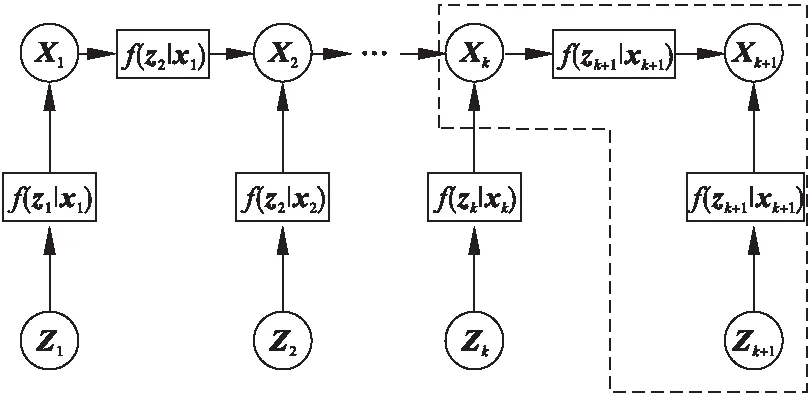
图3 USV位置估计算法中的因子图

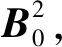
由式(12)可知，f(Xk+1|Xk)到Xk+1的消息为

BI(f(Xk+1|Xk),Xk+1)=

(16)

f(Zk+1|Xk+1)到Xk+1的消息为

BI(f(Zk+1|Xk+1),Xk+1)=

(17)

由式(11)和式(13)可知，Xk传递到f(Xk+1|Xk)的消息为

(18)

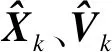
将式(8)和式(18)代入式(17)中，得到预测消息BI(f(Xk+1|Xk),Xk+1)为

BI(f(Xk+1|Xk),Xk+1)=

(19)

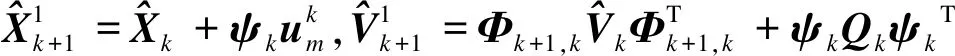
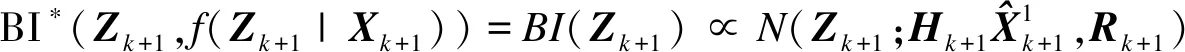
(20)

将式(10)和式(20)代入式(17)中，得到预测消息BI(f(Zk+1|Xk+1),Xk+1)为

(21)

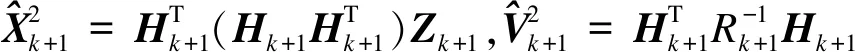
由式(13)可知，

BI(Xk+1)=BI(f(Zk+1|Xk+1),Xk+1)BI(f(Xk+1|Xk),Xk+1)

(22)

由于多个高斯分布的积也是高斯分布，故可以表示为

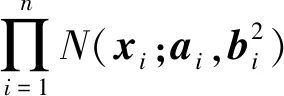
(23)

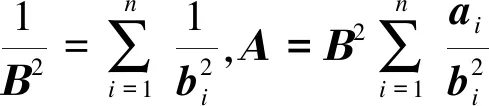
利用式(23)可得出BI(Xk+1)。

4 仿真结果与分析

常用的定位方法包括有只利用外界信息的GPS定位方法、只利用自身信息的航位推算方法和把二者信息结合的EKF算法。为验证基于因子图模型的USV定位算法的有效性，进行Matlab仿真。将本文所提算法与上述三种常用的定位方法进行比较。仿真中设USV位置初始条件为X0=[0，1000，45]T,USV以4kn的速度、以±2°/s的角速度做S型曲线，航行时间为360×t，采样时间间隔为t=1s，速度传感器量测噪声是标准差取为σv=2kn的零均值高斯白噪声，航向角的测量噪声是标准差取σw=5°的零均值高斯白噪声，GPS的观测噪声是标准差取σv=5m的零均值高斯白噪声。

仿真结果如下，图4是USV理想运动轨迹，图5是4种定位方法的误差曲线。

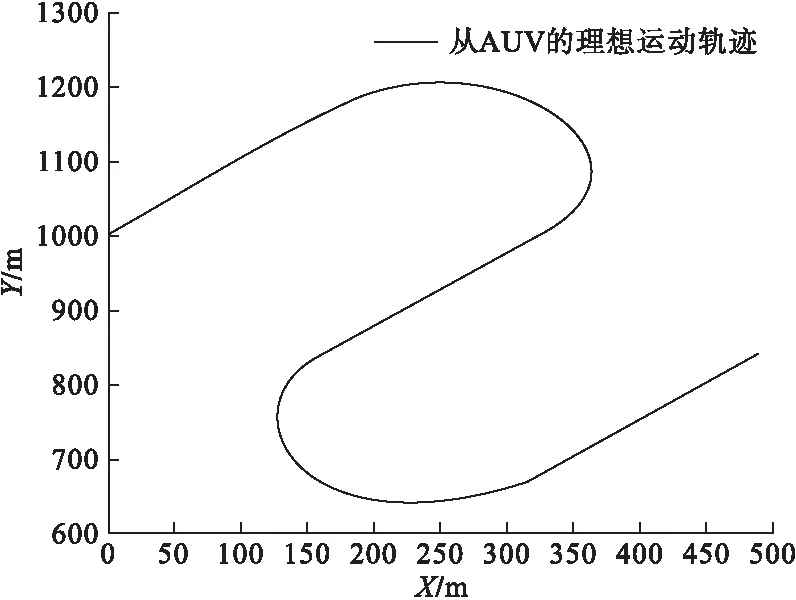
图4 USV理想运动轨迹

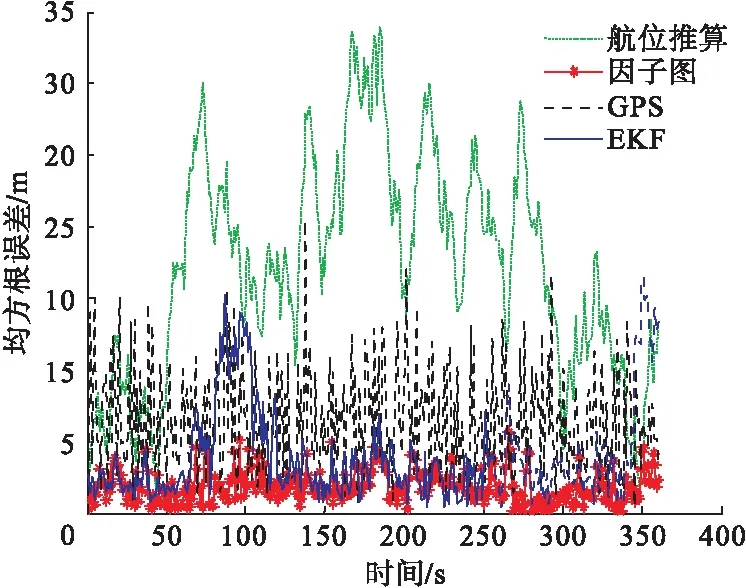
图5 4种定位方法的误差曲线

从图5可以看出利用因子图的USV定位算法可以有效的估计位置信息；当USV在(60，150)时间段内作圆周运动时，EKF算法定位误差增加，而本文所提算法一直都很平稳，受USV的运动状态影响较小。表1是4种定位方法的均方根误差表。

表1 4种定位方法均方根误差

从表1可知，本文所提算法可以有效降低GPS定位结果的误差，精度提升约71%；估计精度明显高于EKF算法的定位精度，精度提升约52%。

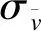
图6为在不同观测噪声协方差情况下，EKF算法与因子图算法的估计误差与观测噪声协方差的关系。

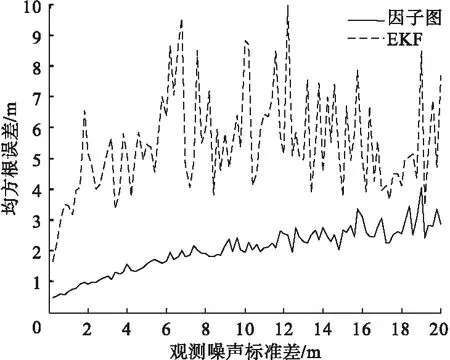
图6 两种定位误差与观测噪声协方差的关系

从图6中可以看出，两种算法的估计误差随观测噪声协方差的增加而逐渐增大，针对定位精度这一性能指标来说，因子图算法明显优于EKF算法，因子图的定位效果明显优于EKF算法。

图7是因子图方法的定位精度提升率与观测噪声协方差的关系。

图7 因子图方法的定位精度提升率与观测噪声协方差的关系

从图7中可以看出，随着观测噪声协方差的增加，定位精度提升率从85%下降到30%，因此可得出，在观测噪声较小情况下，因子图位置估计算法估计效果比EKF算法更好，而且随着观测噪声的降低，因子图算法的优势越来越大，所以本文所提算法更适用于观测噪声较小情况下的USV定位估计。

5 结论

本文提出一种基于因子图的USV位置估计算法，仿真结果表示，此算法可以有效的估计USV位置信息；把此算法与EKF算法进行比较，发现定位精度提升了约52%，而且随着观测噪声的减小，均方根误差比越来越大，可以更好的估计出USV位置信息。随着传感器技术不断提升，传感器的精度也会越来越精确，所以基于因子图的USV位置估计算法更加适用于未来的应用情景。