贝叶斯空间计量模型综述:理论及其应用
李丽辉,温 涛,刘 达
(西南大学 a.数学与统计学院;b.经济管理学院,重庆 400715)
一、引 言
空间计量模型起源于区域科学模型和计量经济模型的共同发展,研究如何在截面数据和面板数据模型中处理空间相互作用和空间结构,是计量经济模型的一个分支。总体而言,空间计量模型的推断理论主要包含估计理论、检验理论及模型选择理论三个方面。LeSage将一种非常特别且在某些领域极为有用的统计学方法——贝叶斯统计方法,运用到空间计量建模中,建立了贝叶斯空间计量模型,突破了空间计量模型经典方法的限制,适用面广,在学术界产生了极大的影响,也是当前空间计量模型理论和应用领域的最新热点[1]。贝叶斯空间计量模型的最新发展包括从截面到面板、从静态到动态、从解析到仿真,其应用范围也涉及经济学各个领域。
本文试图通过对一些相关经典文献著作的简单介绍及梳理,为理论工作者提供一定理论参考,为实证分析研究者提供一种分析类似问题的方法。首先,对空间计量模型的分类系统进行梳理;其次,介绍贝叶斯空间计量模型的推断理论及其应用;再次,介绍贝叶斯空间计量模型选择理论及其应用;最后,指明贝叶斯空间计量模型的发展方向。
二、空间计量模型分类
空间计量经济学起源于区域科学和计量经济学的共同发展,研究如何在截面数据和面板数据中处理空间相互作用和空间结构,是计量经济学的一个分支。最早由J.Paelinck在1972年荷兰统计协会年会大会致词时提出,后经Anselin等人发展,最终形成了学科框架体系。自Krugman在“规模报酬与经济地理”中建立了“中心―外围”模型并将空间因素引入主流经济学分析框架后,经济学家对空间因素的重视程度与日俱增,尤其是2008年Krugman因其“全面整合国际贸易与经济地理的研究成果”而获得诺贝尔经济学奖,使空间计量经济学成为举世瞩目的主流经济学。空间计量经济学被广泛运用至各个社会科学方面,包括社会学、犯罪学、政治学、经济学等。
在经济学领域,涉及的内容包括空间溢出、城市发展和组群经济、贸易和经济增长等,其基本思想是对于某一区域的观察值yi,由于其依赖于其邻接区域某些变量值的加权和加上一些固定效应或随机噪声,因此就用自回归的方式模拟这样的空间交互效应,这使得模型能够清楚地展示出空间依赖性并且在模型的误差项中呈现出一种特殊的方差―协方差结构。
空间计量模型按照数据分布类型主要分为以下几种模型:
(一)高斯模型
这类模型以最常见的联立自回归模型(SAR)模型或者空间误差模型(SEM)为代表,其基本形式可表述为:
y=Xβ+μ;μ=ρWμ+ε;ε~MVN(0,σ2In)
(1)
其中y=(y1,y2,…,yn)′为观测值向量,X为一个n×p阶设计矩阵,β=(β1,β2,…,βp)′为变量系数,In为n维单位矩阵,W为一个行标准化后的邻接矩阵,ρ为空间自回归参数。随机误差项被模拟为其邻接区域的随机误差的加权和再加上一个随机噪声ε,其中随机噪声的分布可用多元标准正态分布(MVN)来刻画。LeSage和Pace探讨了误差项的异方差结构,在他们的推导下,SEM模型可表述为[2]25-41:
y=Xβ+ε′;
ε′~MVN(0,σ2(In-ρW)-1(In-ρW′)-1)
(2)
上述模型就是一个在误差项上有着非对角线方差-协方差矩阵的一般的线性回归模型。
空间计量模型中另外一种重要的模型形式就是空间滞后模型(SLM),LeSage和Pace称之为SAR模型。这种模型中的因变量被模拟为因变量的加权和再加上自变量的线性项与一个随机误差项,模型可表述为:
y=ρWy+Xβ+ε;ε~MVN(0,σ2In)
(3)
还有一种非常常见且应用广泛的空间计量模型是空间杜宾模型(SDM),可表述为:
y=ρWy+Xβ+WXγ+ε;ε~MVN(0,σ2In)
(4)
其中γ是空间滞后自变量WX项的系数向量,即因变量不仅依赖于邻接因变量的加权和,而且依赖于邻接自变量的加权和。
这些模型共同的特点就是误差项的设置都是高斯设置,即均值为0且方差―协方差矩阵结构为SAR模型所设定的结构。SLM和SDM模型在自变量的线性项上有更复杂的结构,空间自相关参数ρ被限制在一定区域上,W作了行标准化。
(二)非高斯模型
当响应变量为二元离散选择变量时,高斯模型不再适用。LeSage等研究了在2005年卡特里娜飓风之后,新奥尔良的一位商人考察周边同行是否重新营业,进而决定自己是否重新开张的问题[3]。他们模拟响应变量yi的形式为:
(5)
其中y*为潜变量,测量了潜在的净收益(如果其大于0,则会重新开张)。潜变量可用SLM模型来模拟,即:
y*=ρWy*+Xβ+ε;ε~MVN(0,In)
(6)
(三)带随机效应的广义线性模型
Nelder和Wedderburn提出了广义线性模型(GLM),该模型能够较好地模拟协变量与空间自相关关系[4]。在这种模型中,响应变量yi设定为来自于指数族分布,均值为μi。自变量向量Xi的线性组合部分和μi之间的关系可通过下述连接函数g(·)建立:
g(μi)=ηi=Xiβ
(7)
如果引入相关随机效应ui,则式(7)变为:
ηi=Xiβ+ui
(8)
u=(u1,u2,…,un)′为多元正态分布,均值为0,方差协方差矩阵为Σ,对矩阵Σ的不同设定就会产生不同的空间依赖性。比如在SAR模型设置中:
Σ=σ2(In-ρW)-1(In-ρW′)-1
(9)
对于这一类模型来说,其模型拟合和解释是更容易的,这是因为这类模型的空间相关参数和自变量的效应项是分开的。比如对于空间滞后模型,自变量部分可写为:
(In-ρW)-1Xβ
(10)
可见X的效应依赖于系数β和空间相关参数ρ。
第一类高斯模型和第二类非高斯模型都可以视为广义线性模型。高斯模型就是限定ρ以后带随机效应的高斯GLM,空间概率模型就是给定ρ的带概率连接函数的二项GLM。
三、贝叶斯空间计量模型推断理论及其应用
贝叶斯统计方法在空间计量分析中的应用可视为空间计量模型领域的一个前沿分支,由LeSage率先提出[1]。与基于经典统计理论的空间计量模型相比,用贝叶斯方法进行空间计量分析具有独到的优势:一是该方法更为普遍,能运用到更加广泛的统计领域;二是该方法允许合理地利用先验信息,更利于直接明确地分析具体问题;三是该方法得到的结果不仅是一个预测值,而是一个完整的未来经济结果的概率分布,这种预测方法比其它预测方法产生的结果更加有用;四是相对于传统统计方法,该方法能更加明确地合理处理不确定因素的问题。空间计量模型按照误差项的分布主要可分为高斯模型、非高斯模型和广义线性模型,而贝叶斯方法在空间计量模型中的应用主要涉及模型的推断与模型比较两个方面,本部分将首先介绍贝叶斯方法应用于这几种空间模型的相关推断理论及其应用。
(一)高斯模型
贝叶斯方法的一个特征是在建模过程中引入先验信息,且与数据分布相结合以生成用于推断的后验分布。基本的贝叶斯方法会在后验分布中创造一个关于样本均值和先验信息的加权矩阵,但权重会受到与先验信息相关的样本数据可得信息数量的强烈影响,在大样本情形下,这能对后验分布的解析提供一个简化的方法。
对于高斯模型,LeSage提出了两类处理的方法:解析法与模拟仿真算法[1]。下面以模型(3)为例进行阐述:
1.解析法
对于模型(3),其似然概率为:
(11)
其中A=(In-ρW)代表矩阵的行列式。为了产生模型参数的后验分布,需要指定参数的先验分布。LeSage采用正态逆伽玛(NIG)分布作为参数β和σ2的先验分布[1];参数ρ的可行范围(1/λmin,1/λmax),其中λmin和λmax分别代表空间权重矩阵的最小、最大特征根。若给定σ、β服从多元正态分布N(c,σ2T),σ的边缘分布服从给定(a,b)逆伽玛分布,则模型(3)可写为:
y=ρWy+Xβ+ε;ε~MVN(0,σ2In)
(12)
π(β,σ2)~NIG(c,T,a,b)=π(β|σ2)π(σ2)
(13)
exp[-{(β-c)′T-1(β-c)+2b}/(2σ2)]
(14)
其中

σ2>0,a,b>0
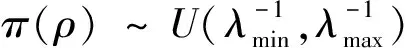
用于识别先验认知的参数就是NIG先验分布中的c、T、a和b等参数。如果在模型中使用了有信息先验分布,问题就会变得复杂,这主要体现在:一是需要指定或分派NIG先验分布中参数的数值;二是后验分布难以分析,因为需要对参数ρ和σ2进行积分以获得参数β的后验表达式;同理,也需对β和ρ积分以得到σ2的后验分布。Hepple根据无信息先验分布得到的简化表达式去寻求贝叶斯SAR模型的解,为解决这类问题提供了一个很好的思路[5]。Hepple基于一个无信息先验分布来替代上文中所提到的NIG先验分布,并假定ρ与β、σ2这些参数相互独立,这样就会得到一个简化后的后验分布如式(15),因此对于β,设置其先验为无信息先验,设定c=0并为β指定一个很大的先验方差T=IK·1010,且β向量参数间协方差为0;通过设定a=b=0,可以得到σ2的无信息先验;对于参数ρ,可以指定一个预先值,这意味着所有在可行范围(1/λmin,1/λmax) 内的结果都是可能的。
根据贝叶斯理论,模型参数的后验分布形式为:
p(β,σ,ρ|D)∝p(D|β,σ,ρ)π(β,σ)π(ρ)

(Ay-Xβ)]π(ρ)
(15)
根据这个简化的后验分布,可将σ作为冗余参数处理并将其从式(15)中积分去掉,由此可得:
p(β,σ,ρ|D)∝|A|{(n-k)s2+
(16)
其中
c*=(X′X)-1X′Ay
s2=(Ay-Xc*)′(Ay-Xc*)/(n-k)
取ρ的条件概率,式(16)就变为一个多维t分布,这样就能对β积分,得到ρ的边缘后验分布为:
(17)
只要已知式(17)中ρ的先验分布,就可按照单变量数值积分方法得到ρ的后验分布,据此做出统计推断。其先验分布的决定形式一般有三种方法: 一是根据ρ在理论上的可行范围(1/λmin,1/λmax)来决定;二是可以给参数ρ指定一个先验范围(-1,1),LeSage和Parent引入了ρ的另一种先验分布Be(α,β),对均匀先验U(-1,1)是一个很好的替代[6];三是考虑由于负的空间依赖对特定问题没有多大意义,可将ρ的先验定义在区间(0,1)上。
如果ρ的先验分布一旦给定,就可做出关于ρ的简化似然函数,按照Pace和Barry提出的方法,可通过使用一个ρ的取值在[ρmin,ρmax]之间的q×1阶向量估计对数似然值[7]。只要提供出一个充分细的栅格q值并对其进行向量化,则通过内推法就可使插值点到达任何需要的精度。该向量可以通过运用Simpson法则等简单方法进行单变量的数值积分。
2.MCMC仿真模拟
解析法是直接对参数后验分布的解析形式进行统计分析,计算繁琐,LeSage采用了另一种目前广泛使用的方法——马尔科夫链蒙特卡罗方法(MCMC),对模型后验分布进行推断[1]。
MCMC抽样算法是基于Markov链对变量进行抽样模拟,由于生成于同一条Markov链,MCMC抽样算法产生的是相依样本。当构造的Markov链收敛至目标分布,即达到稳态,则此分布为所求的后验分布,然后根据稳态后验分布中的样本点计算Monte Carlo积分。因此,MCMC抽样算法的关键是从基于稳态后验分布的概率密度函数中进行抽样。MCMC可以通过检验一个来自后验分布的大的随机抽样来实现,如果来自后验分布p(θ|D)的样本足够大,可以运用核密度估计或者直方图获得概率密度的近似形式,而不需要精确的密度函数解析式,其中两种最为广泛使用的方法是Metropolis-Hastings(M-H)抽样算法和Gibbs抽样算法。
M-H算法依赖于建议分布,对于初始值θ0,在t+1时分布为f(θ|θt),其中θt已知。候选点θ*从建议分布中抽样获得,并且:
如果接受概率为:
(18)
则接受θt+1=θ*;否则θt+1=θt。

c*=(X′X+T-1)-1(X′(In-ρ0W)y+T-1c)
T*=(X′X+T-1)-1
(19)
将抽样参数向量记为β1并代替参数向量β0。
2)利用逆伽玛分布IG(a*,b*)抽样p(σ2|β1,ρ0):
p(σ2|β1,ρ0)~IG(a*,b*)
a*=a+n/2
b*=b+(Ay-Xβ1)′(Ay-Xβ1)/2
A=In-ρ0W
(20)
3)利用接受概率为式(18)的M-H算法,将得到的值记为ρ1并返回到第一步。
从第一步到第三步的一个循环就完成了一次抽样。经过大量抽样,再去除前面的退化期,从每次抽样中收集参数样本,就可利用抽样结果进行后验估计与推断。Hastings证明了MCMC抽样过程在排除最初的若干次抽样后能达到稳定状态,一旦抽样池达到稳定状态,将抽样分布作为后验分布解释就是合理的[8]。
贝叶斯空间高斯类模型的相关理论研究文献一经发表,就因其突出的优点、比较广泛的适应性吸引了学术界的注意,越来越多的学者将其应用到学术研究中,应用领域不断扩展,研究内容不断丰富,也为其他类型的贝叶斯空间计量模型研究奠定了基础。如Seya等为了研究日本从1989—2007年间的收入收敛性,构建了一个空间SDM模型,探讨了其理论背景,做出了收入的空间分布图;模型的估计结果给出了日本在这一时期各个阶段不同的收入差异和几种不同的收敛性[9]。Yu等借鉴了过去研究能源消耗的时间序列和截面数据方法,考虑了能源消耗的时间-空间关系及面板空间数据的异质性,针对中国30个省市从2007—2009年能源消耗数据,用贝叶斯MCMC抽样方法得到后验仿真样本,并用之计算样本边缘分布和后验分布的矩,研究了中国的能源消耗[10]。
(二)非高斯模型

y*~TMVN(μ,Ω)
(21)
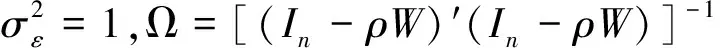
p(β|ρ,y*)∝N(c*,T*)
c*=(X′X+T-1)-1(X′Sy*+T-1c)
T*=(X′X+T)-1
S=In-ρW
p(ρ|β,y*)∝|In-ρW|exp
(22)
在SAR模型中,y*的条件分布服从截尾正态分布。对于非截尾的n维多元正态分布,可以依次从n个条件一元正态分布中抽样以获得n个参数;但Geweke指出该方法不适用于截尾多元正态分布,否则处理SAR模型时会出现错误[12]。

LeSage等使用了截尾多元正态分布的精度矩阵[3],将该矩阵标记为Ψ=Ω-1。由于z为多元正态分布,其中各个元素Zi基于其他所有元素Z-i的条件概率分布可以表示为具有条件均值和条件方差的一元分布,且计算简便。在一定约束下,这些均值和方差的表达式可用于从一元截尾分布中进行抽样,由此就可用Gibbs抽样从多元截尾正态分布中构建一个样本。
对于非截尾多元正态分布,Geweke使用分块对称矩阵的逆构造E(zi|z-i)=γ-iz-i,其中γ-i=-Ψ-i/Ψi,i,Ψ-i是Ψ中第i行除该元素外的其他所有元素。而对于截尾正态分布,使用的条件分布应为:
zi|z-i=γ-iz-i+hivi;hi=(Ψi,i)-1/2
(23)
vi~N(0,1)的抽样服从以下截尾约束:

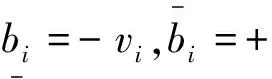
由此可以产生一个由zi(i=1,2,…,n)构成的向量z,在对元素zi进行抽样时,可使用前期抽样的结果z1,z2,…,zi-1。此外,在更新zi时,还会使用从前一次Gibbs抽样中得到的zi+1,zi+2,…,zn。通过对含有n个观测值的向量z进行m次抽样,可以得到y*=v+z(m),其中y*则可以用于从模型参数β和ρ的条件分布中进行抽样。
在对截尾多元正态分布的抽样中,设定MCMC抽样器的迭代步骤m=10,每次MCMC抽样仅需y*的样本值,由于产生y*值时进行了数千次抽样,所得y*相对精确,但Gibbs抽样中,仅需一步即可,即m=1,此时用由前一次MCMC取样器产生的z值。m值的减少将显著减少模型估计的时间,可以提高计算机运行速度。同时,因为该方法能够将大样本数据划分为从一元条件分布中抽取的一系列样本,可以不需要借助大容量计算机内存就可以处理大样本数据。上述过程还可以采用一些其他有效的计算方法,比如可通过使用精度矩阵Ψ,而不需要计算逆矩阵[(In-ρW)′(In-ρW)]-1,从而降低了对电脑内存的要求。
将上述的贝叶斯MCMC方法进行拓展,可以处理有序空间概率单位模型、空间Tobit模型和多项空间概率单位模型等多种非高斯模型,限于篇幅不一一赘述,具体可参见Qiang Zeng等的研究[13]。
非高斯贝叶斯空间计量模型的具体应用可参见:Andrea Amaral等为了研究亚洲20世纪90年代的银行危机,构建了一个空间概率模型用于测度不同国家银行系统间的传染效应,并在空间概率模型中考察了潜变量及其滞后项的空间效应,同时也考察了误差项的空间效应,用Gibbs抽样方法估计模型并分析了这种传染效应的产生机制[14];Changjoo Kim等人建立了一个贝叶斯多元Tobit模型,模拟了家庭成员的交互行为是如何影响其他个体旅行行为的[15]。在他们所采用的数据集中,涉及到个人旅行数据存在大量删失值,此时多元Tobit模型则可以使用截尾多元t条件后验分布对潜在的无法观测的效用进行分析。这些文献涉及经济预测、经济结构分析和经济行为模拟分析等多个领域,为实证分析研究者们提供了极好的借鉴。
(三)广义线性模型
空间广义线性模型中被解释变量与其滞后项和解释变量之间不再是呈线性关系,高斯模型和非高斯模型都可被视为广义线性模型的特殊情形,因此这两类模型都可用常规方法加以处理。对于其他的一些空间广义线性模型,如Griffith研究了一个引入空间依赖的自逻辑斯蒂(autologistic)回归模型[16]:
p(Yi=1|α,WiY)
(24)
其中α为一个能够捕获大尺度变化的参数,可依据Xi来进行设置;ρ为空间自相关参数;Wi为相对于位置i的由wij构成的行向量;行向量Wi构成的空间权重矩阵W为对称的。
该模型的空间自相关性能够被Cliff等提出的联合计数(join-count)统计量所测定[17]179-183。两个1在地理位置相邻记为BB,一个1和一个0地理相邻记为BW,若两个0地理相邻记WW,把这些联合计数统计量标准化就能得到其相应的Z值。进一步地,如果在模型(24)中考虑n×(K+1)阶协变量矩阵X,矩阵X造成了地理二项数据的空间自相关,其均值响应的设置将会使得模型的空间依赖参数值为0;由于变量缺失于均值响应设置,因此空间自相关出现在残差项中,可引入特征向量滤子加以处理。特征向量滤子是一种非参数方法,这种方法利用了空间自相关性的设定偏误,即假设空间自相关性是由具有空间自相关的缺失外生变量带来的;空间自相关潜在于协变量矩阵X,矩阵X造成了因变量Y的空间自相关性,其基本思想是把广义线性回归模型中固有的空间自相关性视为缺失变量效应而将其剔除,从而利用一组空间代理变量来控制空间自相关性。代理变量为二项矩阵W的修正形式矩阵:
(25)
的特征向量,其中I为单位矩阵,1为n×1阶1向量,n为区域个数。
利用空间权值矩阵可以计算出空间滤子的每一个特征向量E1,E2,…,En,这些特征向量代表了不同的空间模式,也相关于给定的空间自相关水平。因此,模型(24)可以被下述模型替代:
(26)
其中K表示n个特征向量的一个子集中所含特征向量的个数,即Ei,K为一个n×K阶矩阵,其列是K个被选择的特征向量。这样,就把模型中的空间依赖效应转换为由Ei,Kβ所表示的大尺度变异项,使得参数ρ为0。可以看到,模型(24)和模型(26)间存在下述关系:
p(Y=1|WY)=p(Y=1|EΛETY)
=p(Y=1|Eδ)
(27)
其中Λ为一个特征值对角矩阵,δ为系数向量。这样的处理方法关注了特征向量空间滤子而避免了处理协变量,大大简化了所要研究的问题。
特征向量空间滤子方法把一个最小充分的特征向量集合作为代理变量施加于线性预测子集合,因此如果考虑到独立性,就可以排除观测值间的空间自相关性。这种方法比MCMC运算更容易操作,参数估计比起拟极大似然估计更为有效,而且由于其对地理二项数据中隐含的自相关模式进行了分解,这使得模型的空间自相关效应能够得到更准确的解释。
四、贝叶斯空间计量模型选择理论及其应用
空间计量模型选择主要分为:空间和非空间模型的比较、不同空间权重结构模型的比较和纳入不同候选解释变量模型的比较。基于贝叶斯统计理论,Zellner建立了进行多个模型比较的方法[18]。该方法设定每个模型的先验概率、回归参数的先验分布,计算后验模型概率,并用于推断不同回归模型与先验信息的一致性,其基本思想考虑m个空间回归模型:M=M1,M2,…,Mm,对于这m个模型给予一个先验概率π(Mi),根据样本的条件分布与参数的先验分布,可以得到第i个模型的后验分布,据此则可计算模型的后验概率。
对于一个空间计量模型,可以把模型和参数的联合后验分布表示为:
(28)
其中π(M)为模型的先验概率,π(η|M)为模型参数在给定模型条件下的条件概率,π(D|η,M)为样本数据的条件分布。视η为冗余参数,则模型的边缘条件分布可以表示为:

(29)
特别地,对于SAR模型,模型参数的后验分布可表示为:
(30)
e=(In-ρW)y-αιn-Xβ
模型参数中β服从条件正态先验N(β0,σ2(gX′X)-1),σ2为倒伽玛分布IG(a,b),截距参数α为无信息先验,ρ为Be(d,d)先验。因此,式(28)可写为:
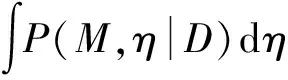
其中
S(ρ)=e(ρ)′e(ρ)
C=gX′X

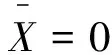
(31)
若仅对p(η|D)中的β和σ2积分,可消掉这两个参数,可以得到:
(32)
其中
A=In-ρW
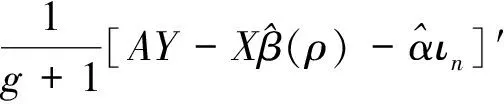
(33)
因此,在考虑模型比较的情况下,可采用贝叶斯理论的后验概率比的思想,对于有m个不同加权矩阵W(i),i=1,2,…,m的情形,根据似然函数和参数的先验分布,每个模型视为是不同的模型,则:
(34)
因此给定不同的模型(空间权重矩阵),就可得到后验模型概率:
(35)
依赖不同模型的后验概率比为:
(36)
该方法的优点在于比较模型的类别广泛,可用于不同的空间权重矩阵的比较,而且不同模型设定比较或不同的解释变量比较,皆可用后验概率比或贝叶斯因子来比较非嵌套模型。 但是,采用上述方法时需要注意的问题是,要求避免Lindley提出的一个悖论:当比较不同数量参数的模型时,这些参数依赖扩散先验分布,无论样本数据信息如何,简单的模型比复杂模型更好,即具有相同数量参数的两个模型可以用扩散先验来比较,但对包含参数个数变化的模型比较必须开发和采用先验策略。
对于包含不同解释变量的替代线性回归模型进行贝叶斯模型平均,Madigan和York介绍了一种马尔科夫链蒙特卡罗模型组成的(MC3)方法用于空间回归模型[19]。对于有k个解释变量的回归模型,有2k种可能方式来选择或排除回归元。因此,模型平均需要纳入足够多的变量以克服遗漏变量偏误和因包括冗余变量而降低模型的精度。
该方法的原理是建立一个策略随机马尔科夫链过程,用M代表模型目前的状态,对于每个M∈M,定义一个邻域nbd(M),其中包括了模型M和其他模型的集合族,该集合族中的集合较之M具有更多或更少的边缘。同时,定义一个转移概率矩阵q,若对于一切M′∉nbd(M),则q(M→M′)=0;对一切M′∈nbd(M),则q(M→M′)=常数。按照接受概率:
(37)
持续进行抽样,并得到建议模型M′。在贝叶斯方法中,将解释变量设定的随机性融入估计和推断的解决方法是平均不同模型的设定,这与很多依赖单一模型设定的方法形成对比,采用不同的模型比较准则得到最优模型。程序确定了与特定解释变量相关的模型,对每一个模型指定了一个后验模型概率,其指标可以直接计算,易于操作,结果更具有稳健性,不受样本量大小的限制。
有关贝叶斯空间计量模型选择的其他论述还可参见陶长琪等的研究,他们比较了传统的方法与MCMC方法,仿真研究显示MCMC方法的检验效度更高[20]。在模型选择的具体应用方面,曾召友等基于贝叶斯空间面板计量模型理论,研究了中国电信服务的外溢性,对空间面板计量模型簇中的嵌套和非嵌套情形进行了整合处理,使得研究结果具有稳健性[21]。
五、结 语
空间计量学从20世纪80年代诞生以来,受到了计量经济学家的广泛关注,经历了从萌芽到成熟、从边缘到主流的一个飞跃;众多统计学、经济学、数学和计算科学研究学者为其方法体系的建立、发展和完善做出了大量的努力,其中贝叶斯方法的引入为空间计量模型的研究注入了新的活力。传统的空间计量模型设定参数是确定的,在这种设定下建立的模型往往不符合现实经济结构和行为方式,从而导致模型估计结果偏差很大,预测结果极为不准确。如今,贝叶斯统计方法与计算科学的飞速发展可以很好地解决这一问题,这不得不让经济学家们开始审视空间模型参数随机性的问题。从这个意义上讲,贝叶斯空间计量模型的发展与应用无疑会对未来经济科学的研究范式革新与理论边界扩展产生影响。从现有文献来看,贝叶斯空间计量模型对于一些常见模型已获得一定有意义的成果,可将其运用于经济研究各个领域,并且用其分析的结果较为准确;从模型的灵活性来看,贝叶斯空间计量模型也优于非贝叶斯模型。然而在实际问题运用中,贝叶斯统计分析方法在模型推断和模型选择中的应用还是有限制的,这种限制是由于参数数量增加带来的计算困难,而不是传统方法的自由度不足。
因此,贝叶斯空间计量模型的理论与应用研究也面临着一些巨大的挑战。首先,空间计量模型大数据问题:目前的空间计量模型所采用的数据基本是人工记录数据,但随着科学技术的进步,未来的空间计量模型会利用到自动记录数据。在自然或社会科学中的传感器系统能够从时间维度、空间维度和个体维度提供更大量的数据,目前的贝叶斯空间计量模型的理论方法则不适用于这种大数据情形。其次,随着空间计量大数据时代的到来,与之相应的就是对计算技术要求的提高。要能够处理大数据中复杂的时空交互反应,就必须要求有更高效、更快速、更准确的新的计算技术,例如分布式计算技术、云计算和手持装备的运用。
中国学者对贝叶斯统计理论与方法的研究相对较晚,与西方国家相比尚有很大差距,这主要是因为贝叶斯方法较之经典统计方法在中国的应用较少,该方法还不为大家所熟悉;并且其计算复杂,对于高维数据计算尤为困难,缺乏相应的软件支撑,这妨碍了贝叶斯方法在实际问题中的使用。目前而言,贝叶斯空间计量模型既有广阔的发展空间,又面临前沿问题的挑战,这正是促进其不断完善、不断进步的动力。
[1] LeSage J P.Bayesian Estimation of Spatial Autoregressive Models[J].International Regional Science Review,1997,1&2(20).
[2] LeSage J P,Pace R K.Introduction to Spatial Econometrics[M].New York:CRC Press,2009.
[3] LeSage J P,Kelley Pace,R,Lam N,et al.New Orleans Business Recovery in the Aftermath of Hurricane Katrina[J].Journal of the Royal Statistical Society.Series A,2011,174(4).
[4] Nelder J,Wedderburn R.Generalized Linear Models[J].Journal of the Royal Statistical Society.Series A,1972,135(3).
[5] Hepple L W.Bayesian Techniques in Spatial and Network Econometrics 1,Model Comparison and Posterior Odds[J].Environment and Planning A,1995,27(2).
[6] LeSage J P,Parent O.Bayesian Model Averaging for Spatial Econometrics Models[J].Geographical Analysis,2007,3(39).
[7] Pace R K,Barry Ronald.Quick Computation of Spatial Autoregressive Estimators[J].Geographic Annal,1997,29(3).
[8] Hastings W K.Monte Carlo Sampling Methods Using Markov Chains and Their Applications[J].Biometrika,1970,57(7).
[9] Seya Hajime,Tsutsumi Morito,Yamagata Yoshiki.Income Convergence in Japan:A Bayesian Spatial Durbin Model Approach[J].Economic Modelling,2012,29(1).
[10] Yu Yanpin,Li Xi, Qian Zhengming.A Study on China's Energy Consumption by Bayesian Spatial Econometric Model[J].Energy Procedia,2012(16).
[11] Albert J H,Chib S.Bayesian Analysis of Binary and Polychotomous Response Data[J].Journal of The American Statistical Association,1993,88(22).
[12] Geweke J.Efficient Simulation from the Multivariate Normal and Student-t Distributions Subject to Linear Constraints and the Evaluation of Constraint Probabilities[C].In Proceeding of 23rd Symposium on the Interface Between Computing Science and Statistics,Interface Foundation of North America Inc.Fairfax,1991.
[13] Qiang Zeng,Wei Huiying,Huang Helai.A Bayesian Spatial Random Parameters Tobit Model for Analyzing Crash Rates on Roadway Segments[J].Accident analysis and Prevention,2017,100(3).
[14] Andrea Amaral,Margarida Abreu,Victor Mendes.The Spatial Probit Model—An Application to the Study of Banking Crises at the End of the 1990's[J].Physica A:Statistics Mechanics and Its Applications,2014,415(415).
[15] Changjoo Kim,Olivier Parent.Modeling Individual Travel Behaviors Based on Intra-household Interactions[J].Regional Science and Urban Economics,2016,57(5).
[16] Griffith D A.A Spatial Filtering Specification for the Auto-logistic Model[J].Environment and Planning,2004,36(10).
[17] Cliff A D,Ord J.Spatial Processes[M].London:Pion,1981.
[18] Zellner A.Bayesian Econometrics[J].Econometrica,1985,53(2).
[19] Madigan D,York J.Bayesian Geographical Models for Discrete Data[J].International Statistical Review,1995,63(2).
[20] 陶长琪,杨海文.空间计量模型选择及其模拟分析[J].统计研究,2014,31(8).
[21] 曾召友,龙志和,董大勇.基于Bayes理论的空间面板计量模型遴选框架——以中国电信服务外溢性分析为例[J].统计与信息论坛,2010(3).

