分位数回归下的因果关系检验
伍兴国
(1.暨南大学 经济学院,广东 广州 510632;2.东莞职业技术学院 财经系,广东 东莞 523808)
一、引 言
目前,对用Granger因果关系来检验变量之间是否为一种“真正”的因果关系尚存在较大的争议,但是如果基于统计学的考虑,以此来判断各种经济变量的“前因后果”的联系, Granger因果关系检验已经在实践中得到了广泛认可,如经济运行中先行指标的选择。
通常检验变量之间Granger因果关系是以通过定义变量间非因果关系作为原假设,只有当统计量拒绝原假设才接受变量之间可能存在因果关系。尽管Granger因果关系最早是基于信息集进行的,而要搜集完整的信息集是不可能做到的,因此演变为仅考虑统计意义上的因果关系,即根据条件分布函数来定义,因处理分布函数也较为复杂,最终简化为以条件分布函数的均值或者期望来进行检验变量的因果关系[1-2]。Granger、Robins、Engle[3]与Cheung、Ng[4]将此发展到基于条件方差来检验变量的因果关系,而Hiemstra和Jones又进一步将其扩充到检验变量的非线性因果关系[5],这些检验虽已广泛用于研究文献中[6-7],但仅局限于检验条件分布上均值或方差的因果关系,而均值和方差作为分布函数的小部分统计量,因此需要考虑到条件分布的其他特征。Diks和Panchenko也给出了用Hiemstra和Jones的检验方法来检验Granger非因果关系失效的案例[8]。因此,笔者考虑以条件分布的其他特征来检验变量之间的因果关系。
本文从条件分位数出发来探讨和研究变量的因果关系。首先定义在所有的分位数上将变量间存在的非因果关系作为原假设,其检验方法不再是通过普通线性回归,而是利用分位数回归来进行[9][10]26-66,其检验思路就是检验系数的显著性,即以Koenker和Machado的Sup-Wald检验法来实现[11],这种分位数因果检验的显著意义在于:考虑了整个分位数簇的参数变化过程,因此与条件分布中的因果关系检验的理念是一致的;类似于分位数回归模型区别于一般普通回归模型,用一簇回归模型取代一条回归模型。分位数因果检验与经典的Granger因果检验的方法区别在于:不仅仅停留在条件分布均值上的因果关系,而是将其扩展到检验变量在不同条件分位数上的因果关系,因此能够更全面地认清和确认变量间的因果关系。
二、Granger因果关系检验
Granger首次提出了变量的因果关系,其定义需要变量的完整信息集与时间先后顺序,由于完整信息集在实际中几乎不可能取到,故退化为依据分布函数来决定,而通常所说的随机变量x不是随机变量y的格兰杰原因是指:
Fyt[η| (Y,X)t-1]=Fyt[η|Yt-1]
(1)
∀η∈IR
其中Fyt[·|F]为yt的条件分布,(Y,X)t-1是yi和xi由过去一直到t-1期生成的信息集,即变量x的历史信息并不能影响和改变yt的条件分布。如果式(1)不成立,则认为变量x是随机变量y的格兰杰原因;同时,从式(1)也可以看出其定义的格兰杰因果关系其实是分布上的因果关系,因估计和检验条件分布相当有难度,通常的做法是检验式(1)的必要条件,即:
E[yt|(Y,X)t-1]=E[yt|Yt-1]
(2)
其中E[yt|F]为条件分布Fyt[·|F]的期望或者条件均值。当式(2)成立,并在得出变量x不是随机变量y的格兰杰原因的结论时需要格外注意,因为条件均值上的非因果关系只是条件分布上的非因果关系的必要条件,所以评判变量之间的非因果关系是有风险的;相反,如果式(2)不成立,可以得出随机变量x是随机变量y的格兰杰原因的结论是可靠的,因为至少在条件均值上是如此。类似地,与定义在方差上或者其他矩上的非因果关系的道理是一样的。
式(2)的检验一般是假定E[yt|(Y,X)t-1]是线性模型,即:
(3)
模型的自变量取于变量yt的历史信息Yt-1和xt的历史信息Xt-1,这里假设变量y的滞后为p阶(yt-1,yt-2,…,yt-p),变量x的滞后为q阶(xt-1,xt-2,…,xt-q),因此检验条件均值的因果关系就转化为检验原假设:所有系数βj=0(j=1,2,…,q)是否成立,亦即变量x所有滞后阶数是否对变量yt的条件均值有显著影响。在原假设成立的条件下,其统计量服从F分布,即:
(4)
其中SSE0为施加约束的残差平方和,SSE1为未施加约束的残差平方和。当统计量大于F分布的临界值则拒绝原假设,可以认为变量x是随机变量y的格兰杰原因;当拒绝原假设仅仅只能说明在条件均值上有因果关系的证据,接受原假设并不代表变量之间无因果关系,因为有可能这个因果关系是基于条件分布的其他特征。
三、分位数回归下的因果关系检验
传统的Granger因果检验是通过最小二乘回归方法和F检验来进行的,其诸多性质更多依赖于正态分布的假设,这很有可能会导致结论不可靠。针对分位数回归而言,可以取不同分位数进行回归,而分析不同层次下的因果关系更能反映条件分布的全貌,其结果对离群值更稳健,同时对于非正态分布而言,分位数回归估计量更有效。
(一)分位数回归下因果关系的检验形式
假定一个分布完全由其分位数来确定。定义Qyt[τ|F]为条件分布函数Fyt[·|F]的第τ分位数,检验分布上的非因果关系依据条件分位数来进行,即式(1)转化为:
Qyt[τ|(Y,X)t-1]=Qyt[τ|Yt-1]
(5)
∀τ∈(0,1)
如果式(5)成立,则认为在所有的分位数上没有证据能说明随机变量x是随机变量y的原因;也可以将注意力集中在部分分位数区间[a,b]⊂[0,1],即关系式为:
Qyt[τ|(Y,X)t-1]=Qyt[τ|Yt-1]
(6)
∀τ∈[a,b]
当然也可以指定分位数τ0,其关系表达式为:
Qyt[τ0|(Y,X)t-1]=Qyt[τ0|Yt-1]
(7)


(8)
这里的系数向量为θ(τ)=[α0(τ),α(τ)′,β(τ)′]′,为k=1+p+q维,et(τ)为残差项。为防止伪回归,这里也要求变量为平稳时间序列,或者为存在协整关系的非平稳序列。回归模型系数向量θ(τ)的估计一般则通过极小化下式,即非对称加权绝对离差和:

(9)
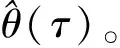
H0∶β(τ)=0 ∀τ∈(0,1)
(10)
(二)估计参数的性质
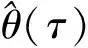
(11)
其中T为样本量,→D为依分布收敛,
其中ft和Ft分别为在给定zt-1下yt的密度函数和分布函数,一般采用核函数进行估计。如果定义Bq为独立的布朗桥,布朗桥Bq(τ)在分布上又等价于[τ(1-τ)]1/2N(0,Iq),因此式(11)可以表示为:
(12)
(三)构建分位数因果关系的统计量


(13)


[τ(1-τ)]
(14)
为了检验原假设是否成立,Koenker和Machado建议在不同分位数水平下检验系数的显著性,需要在不同的分位数上计算Wald统计量的最大值, 即Sup-Wald值。定义‖·‖为欧几里得范数、⟹为弱收敛,根据Koenker和Machado的结论,Wald统计量在紧集Λ⊂(0,1)上一致成立,即:
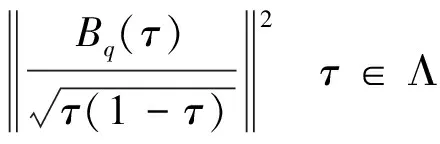
(15)
因此Sup-Wald检验统计量的极限性质为:
(16)
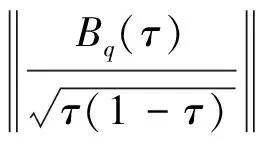
(17)
当n充分大时,在Λ=[ε,1-ε]的性质将很好地接近Sup-Wald的极限性质。
更一般地,可以通过在(a=τ1<…<τn=b)上的WT(τi)极大值检验如下原假设:
H0∶β(τ)=0 ∀τ∈[a,b]
(18)
区间[a,b]一般为感兴趣的分位数范围。如果存在∀τ∈(0,1)拒绝原假设,而在∀τ∈[a,b]又不能拒绝原假设,一般认为这种因果关系来自区间[a,b]之外。
(四)临界值的计算和模拟
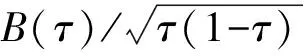
(19)
这里的s1=a/(1-a),s2=b/(1-b),Wq为q维的独立布朗运动。对于某些q与s2/s1的值可以查到[12],这里用模拟方法提供了自变量个数从q=1到q=10,置信水平分别为α=0.1、α=0.05、α=0.01,模拟次数为100 000次的临界值,见表1。

表1 统计量Sup-Wald的模拟临界值表
注:分位数区间范围为[0.15,0.85]
对于分位数回归模型(8)来说,具体的检验又可以分为两种方式:一是单个系数的检验,即分别检验自变量滞后参数的显著性,虚拟假设为βj=0,j=1,2,…,q,如果在某个分位数上不成立,则说明变量x是变量y的原因;二是待检参数的联合检验,虚拟假设为β1=β2=…=βq=0,如果在所有的分位数上不严格成立,则说明变量x是变量y的原因。相比于单系数检验,参数联合检验的效率相对更高,其结论也更可靠。相似地,将随机变量x和y位置颠倒,则可检验y是否为x的原因。
变量的因果关系是客观存在,只是这种影响可能表现在条件分布的不同特征上,例如均值、方差、分位数,而与检验模型和分位数是无关的。当这种因果关系表现在条件分布其他特征上,其基于条件均值的Granger检验又不显著,因此有可能出现误判;当选择普通最小二乘的Granger因果检验与分位数因果检验存在检验结论不一致时,应当认为变量之间有因果关系存在,尤其当Granger因果检验否定变量之间的因果关系而分位数因果检验认为有因果关系时,说明变量x的历史信息对y条件分布的影响不是集中在均值上而是在某些分位数上;另一方面,当Granger因果检验认为变量有因果关系,而且在绝大部分情况下分位数检验也能检验出变量之间有因果关系,如果没有检验出因果关系,则可能是由于样本量较少的缘故。
四、实证分析
自改革开放以来,随着中国经济的快速发展,人民的生活水平得到了明显改善,消费能力也明显上升,同时也促进了经济的不断发展。根据调查数据可知,中国城镇居民的人均可支配收入大幅提高,已经从1980年的447.6元增至2016年的33 616.0元,提高了70倍;而城镇居民的人均消费性支出也从1980年的412.44元增加到2016年的23 079元,增长了接近56倍,说明在收入增加的同时,居民的消费也在逐年增长,虽然每年的增长速度及增长量均有较大差异,但总体上来说还是呈现不断提高的态势。可见,推动国民消费进而促进国民经济增长,是政府一直以来普遍关注的问题。
在经济学中,绝大多数消费理论认为:收入是影响消费的最主要因素,收入的变化决定着消费的变化,著名的消费理论有:莫迪利安尼生命周期假说认为,消费支出取决于预期的终身收入、平均消费倾向与边际消费倾向大致相等;弗里德曼持久收入理论认为,消费支出取决于持久收入;杜森贝里的相对收入假说认为:消费水平主要取决于相对收入水平,除了当期收入外,还与曾经的高峰收入有关,同时消费具有惯性,过去的消费水平会影响当期的消费水平,认为消费存在棘轮作用,即收入绝对增加对消费的增加作用较大,而收入绝对减少对消费减少的作用并不明显,因为居民宁愿减少储蓄而稳定消费。
目前,国内研究收入与消费的关系主要集中在两者的协整关系上:如苏明君对辽宁地区城镇居民收入与消费的分析和陈保玲对安徽省城镇居民可支配收入与消费的分析,均得出两者之间具有协整关系的结论[13-14]。有一部分学者研究了两者的格兰杰因果关系,如卢学法分别对相关省份数据进行了协整检验和因果关系研究,认为收入是消费的单向Granger原因[15];刘亚铮等人比较了中国城镇和农村居民的收入和消费关系,发现存在显著差异,尤其在城镇居民中,前期的消费水平对当期消费水平影响较大,并且认为消费是收入的单向Granger原因[16]。也有少数学者在不同收入下对消费支出进行分析,如张肃分析了不同收入省份的消费水平存在显著差异[17]。 由于选择的样本存在差异和研究方法的不同,可见分析所得结论也不一致。
前期许多学者将数据以取自然对数的形式进行分析,其主要优点在于可以不改变原始变量的协整关系,还能消除数据可能的异质性,但是取对数考虑的是增长率,即弹性。本文以中国城镇居民的人均可支配收入与人均消费性支出为分析对象,以其增量为分析变量,选取1980—2016年的年度数据,数据来源于同花顺金融数据库IFIND。本文基于增长量考虑,所以选择的数据为人均可支配收入Xt和人均消费性支出Yt,以变量ΔXt和ΔYt表示为Xt和Yt的增量,用Δ2Xt和Δ2Yt分别表示ΔXt和ΔYt的一阶差分。
(一)数据ΔXt和ΔYt的单位根检验
在时间序列中应用经典的线性回归,首先需要考虑序列的平稳性,检验方法为单位根检验,其原因在于对非平稳序列有可能出现虚假回归或伪回归的现象,这里采用常用的ADF检验法,其滞后阶数由SIC准则确定。先对序列ΔXt和ΔYt进行检验,依据表2的结论,说明ΔXt和ΔYt为非平稳序列,而Δ2Xt和Δ2Yt的检验统计量均小于1%的临界值,说明ΔXt和ΔYt均为1阶单整序列I(1)。
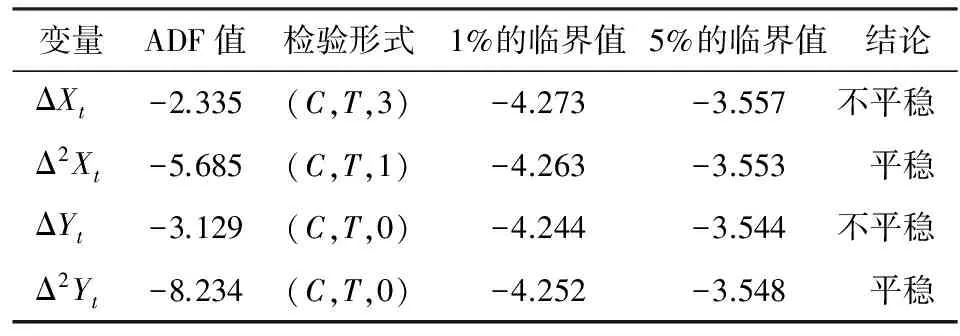
表2 序列单位根检验表
注:Δ是差分算子;检验形式中的C、T、K分别表示常数项、时间趋势项、滞后阶数。
(二)数据ΔXt和ΔYt的协整检验
由于ΔXt和ΔYt为同阶单整序列,可以检验两者是否存在协整关系,采用EG两步检验法,即检验回归方程残差是否为平稳序列,如果残差平稳则说明两者具有长期均衡的协整关系。
首先建立OLS回归方程:

t=(1.479)(23.877)
(20)
其中调整的R2=0.942、F=570.153,根据回归结果可以看出回归方程非常显著,其中DW=2.076,说明残差基本上无自相关的存在。

(三)Granger因果关系检验
格兰杰指出两个I(1)过程如果具有协整关系, 那么一定存在某种因果关系来支撑这种长期均衡,其方向可能是单向也可能是双向的。分析变量条件均值上的因果关系就是采用格兰杰因果检验,而其对滞后阶数非常敏感。对ΔXt和ΔYt进行格兰杰因果检验,其滞后阶数为1阶是依据VAR的最优滞后阶数来确定(结论见表3),即接受人均消费性支出增量ΔYt不是人均可支配收入增量ΔXt的格兰杰原因,而拒绝人均可支配收入增量ΔXt不是人均消费性支出增量ΔYt的格兰杰原因。为保守起见,也对滞后二阶进行格兰杰因果检验,结论依然如此,不过P值稍大而已,但在5%的临界值下可拒绝原假设。
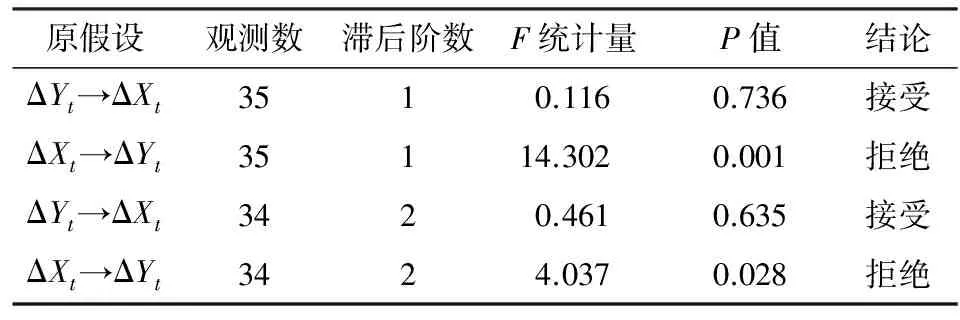
表3 人均可支配收入和人均消费性支出的Granger因果检验表
(四)分位数下的因果关系检验
首先考虑具有协整关系的时间序列ΔYt与ΔXt,在指定分位数τ上单个系数的检验。人均消费性支出增量ΔYt对其自身的滞后值和人均可支配收入增量ΔXt的滞后值进行分位数因果检验,即:

(21)

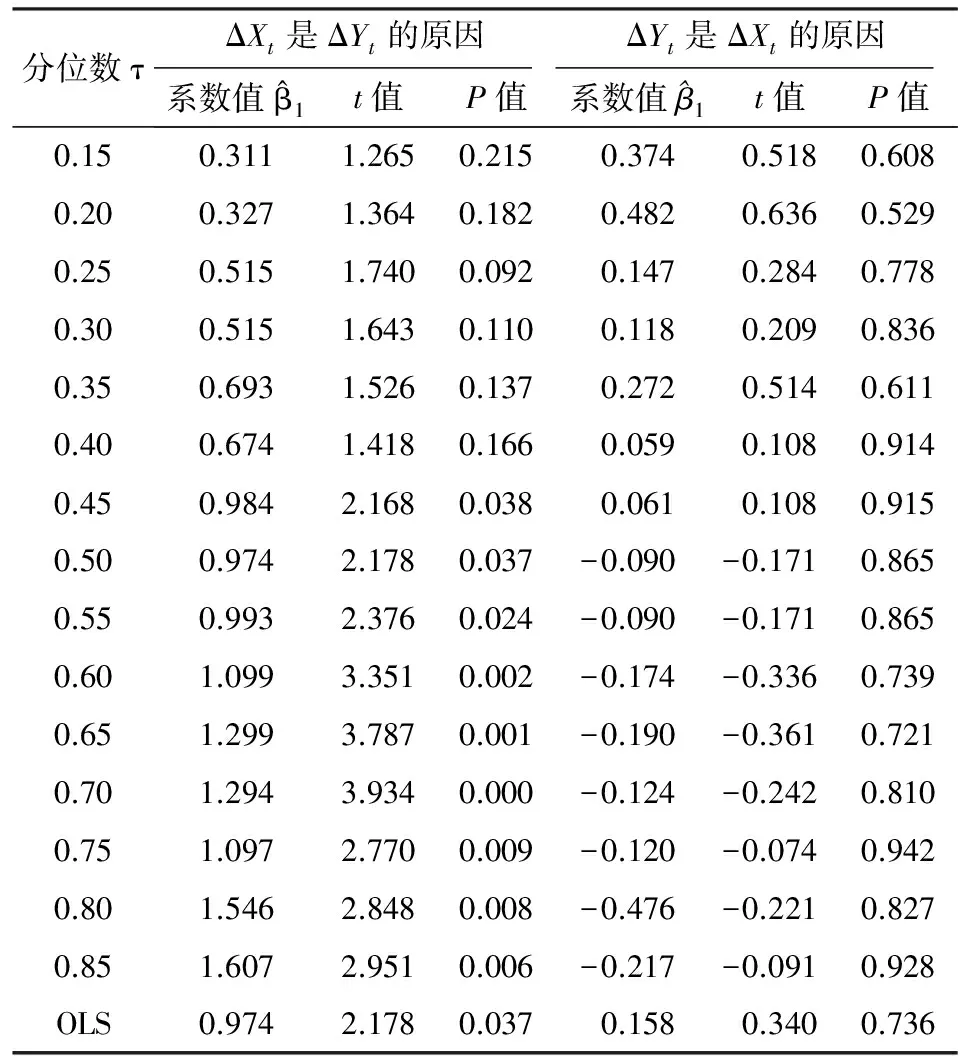
表4 人均可支配收入增量ΔXt和人均消费性支出增量ΔYt的分位数回归统计表
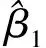
为分析分位数τ在(0.15,0.85)范围内的联合检验,将分位数按照每次0.01的速度递增,采用MATLAB平台计算Sup-Wald统计量值。首先,分析人均可支配收入增量ΔXt是人均消费性支出增量ΔYt的原因,Wald统计量最大值为10.20,在5%的置信水平可拒绝估计参数β1=0的原假设;其次,分析人均消费性支出增量ΔYt是人均可支配收入增量ΔXt的原因,检验统计量的最大值为1.995,根据表1的临界值,即使在10%的置信水平下仍然不能拒绝原假设,因此没有充分的理由能说明人均消费性支出增量ΔYt是人均可支配收入增量ΔXt的原因。很显然,其结论与单个系数检验是一致的,不过Sup-Wald是所研究分位数上的综合检验结果,而单个系数检验更能指明变量的因果关系位于分位数的哪些区域。
五、结 论
传统的Granger因果检验建立在最小二乘法基础上,检验变量位于条件分布均值上的因果关系,这种检验操作相对简单,结论比较直观,但是分析作用有限,尤其当条件分布上有其他特征的因果关系存在时,由于均值的原因可能将这种因果关系给湮灭掉,造成均值检验统计量没有足够的说服力。鉴于此,笔者认为分位数回归下的因果关系检验则能更多地考虑到条件分布上的不同位置,并从不同的层次水平上反映变量间的因果关系。
在此研究基础上,本文分析了全国城镇居民的人均可支配收入增量和人均消费性支出增量的关系,两者之间不仅存在协整关系,同时人均可支配收入增量是人均消费性支出增量的单向因果关系,但是这种因果关系影响是不同的:即在低分位数段,人均可支配收入增量是人均消费性支出增量的因果关系并不显著,说明城镇居民人均消费性支出增量相对幅度不大,前期的人均可支配收入增量对当期消费影响较小;而只有在较高分位数上,城镇居民人均消费性支出增量相对幅度较大,前期的人均可支配收入才对当期人均消费性支出增量影响显著,而相对消费支出增量水平越高,上期的可支配收入增量对其影响效果越大。同时,本文还分析了人均消费性支出增量是否为人均可支配收入增量的原因,无论是在哪个分位数或者均值上,没有理由说明前期的支出增量能影响到收入增量。
在2012年11月,党的第十八次代表大会报告中首次明确提出收入倍增计划,即“2020年实现国内生产总值和城乡居民人均收入比2010年翻一番”。 政府把大幅提高居民收入作为发展经济的核心目标,而提高居民的消费水平、最终促进经济发展,也正是本文的研究所在。
[1] Granger C W J.Investigating Causal Relations by Econometric Models and Cross-Spectral Methods[J].Econometrica,1969,37(3).
[2] Granger C W J.Testing for Causality:A personal Viewpoint[J].Journal of Economic Dynamics & Control,1980,2(1).
[3] Granger C W J,Robins R P,Engle R F.Wholesale and Retail Prices:Bivariate Time Series Modeling with Forecastable Error Variances [J].Model Reliability,1986.
[4] Cheung Y W,Ng L K.A Causality-in-Variance Test and Its Application to Financial Market Prices [J].Journal of Econometrics,1996,72(1/2).
[5] Hiemstra C, Jones J D.Testing for Linear and Nonlinear Granger Causality in the Stock Price-Volume Relation [J].Journal of Finance,1994,49(5).
[6] Fujihara R A, Mougoué M.An Examination of Iinear and Nonlinear Causal Relationships Between Price Variability and Volume in Petroleum Futures Markets [J].Journal of Futures Markets,1997,17(4).
[7] Lee B S, Rui O M.The Dynamic Relationship Between Stock Returns and Trading Volume:Domestic and Cross-Country Evidence [J].Journal of Banking & Finance,2002, 26(1).
[8] Diks C,Panchenko V.A Note on the Hiemstra-Jones Test for Granger Non-Causality [J].Studies in Nonlinear Dynamics & Econometrics,2005,9(2).
[9] Koenker R,Bassett G.Regression Quantiles [J].Econometrica,1978,46(1).
[10] Roger Koenker.Quantile Regression [M].Cambridge:Cambridge University Press,2005.
[11] Koenker R.Goodness of Fit and Related Inference Processes for Quantile Regression [J].Journal of the American Statistical Association,1999,94(448).
[12] David M,De Long.Crossing Probabilities for a Square Root Boundary by a Bessel Process [J].Communication in Statistics-Theory and Methods,1981,10(10).
[13] 苏明君.辽宁省城镇居民消费与收入关系的协整研究 [J].东北财经大学学报,2002(4).
[14] 陈保玲.安徽省城镇居民可支配收入与消费之间的计量分析 [J].内蒙古农业大学学报:社会科学版,2011,13(3).
[15] 卢学法.浙江省城镇居民收入与消费关系的协整和因果性关系研究 [J].统计科学与实践,2005(1).
[16] 刘亚铮, 张昭.城乡居民消费水平与收入水平比较研究——基于VAR模型和Granger因果检验 [J].湖南财政经济学院学报,2014,30(4).
[17] 张肃.中国城镇居民信息消费水平估计与收敛性分析[J].统计与信息论坛,2016(9).
——基于北京市的实证分析

